
1
Jerzy Czesław Ossowski
Katedra Ekonomii i Zarz dzania Przedsi biorstwem
Wydział Zarz dzania i Ekonomii
Politechnika Gda ska
XI Ogólnopolska Konferencja Naukowa nt. Mikroekonomia w teorii i praktyce,
Katedra Ekonometrii i Statystyki , Wydział NEiZ, Uniwersytet Szczeci ski,
winouj cie 18-20 wrze nia 2003 r.,
MODEL MULTIPLIKATYWNY A REDNIA GEOMETRYCZNA
ZAŁO ENIA, ESTYMACJA, WERYFIKACJA I INTERPRETACJA
1. OGÓLNA POSTA MODELU MULTIPLIKATYWNEGO I JEGO SKŁADOWE
Załó my, e zmienna y
t
dla ka dego
t=1,2,3,...,n przyjmuje jedynie warto ci dodatnie.
Załó my ponadto, e zmienna ta jest opisywana przez k zmiennych
x
ti
(
i=1,2,...,k). W tej
sytuacji wygodnie jest zapisa model ekonometryczny w nast puj cej postaci:
t
t
t
v
)
x
(
g
y
⋅⋅⋅⋅
====
(1)
Funkcj g(x
t
) zdefiniujmy nast puj co:
(((( ))))
b
t
x
k
1
i
ti
x
i
b
0
b
t
e
e
x
g
====
====
====
++++
(2)
gdzie:
]
x
.
.
.
x
x
1
[
x
tk
2
t
1
t
t
====
- wektor wierszowy zmiennych obja niaj cych,
]
b
.
.
.
b
b
b
[
'
b
k
2
1
0
====
- transponowany wektor kolumnowy parametrów strukturalnych.
Ponadto uznajmy, e zmienne
x
ti
oraz parametry strukturalne s nielosowe. Mo emy tym
samym uzna , e funkcja
g(x
t
) jest nielosowym, systematycznym składnikiem modelu (1).
Zauwa my, e dla ka dej warto ci zmiennych
x
ti
oraz dla ka dej warto ci parametrów
strukturalnych b
i
składnik systematyczny modelu przyjmuje warto ci dodatnie, co zapiszemy
nast puj co:
(((( ))))
0
x
g
,
t
t
x
Λ
Λ
Λ
Λ
Λ
Λ
Λ
Λ
ββββ
(3)
W zarysowanych warunkach zmienn
v
t
nazwiemy losowym multiplikatywnym składnikiem
zakłócaj cym modelu (1). Zauwa my, e składnik losowy
v
t
wskazuje na udział zmiennej

2
endogenicznej
y
t
w poziomie wyznaczonym przez wielko składnika systematycznego, jako
e:
0
)
x
(
g
y
v
t
t
t
>>>>
====
(4)
Uwzgl dniaj c fakt, e zmienna
y
t
i jej składnik systematyczny
g(x
t
) oraz składnik
zakłócaj cy v
t
przyjmuj jedynie warto ci dodatnie, model (1) mo emy obustronnie
zlogarytmowa i przedstawi w nast puj cej postaci:
t
t
t
u
)
x
(
g
ln
y
ln
++++
====
,
(5)
gdzie:
b
x
)
x
(
g
ln
t
t
====
,
(6)
t
t
v
ln
u ====
.
(7)
Poniewa
u
t
jest logarytmem zmiennej
v
t
, wi c je li zmienna
u
t
ma rozkład normalny, to
zmienna
v
t
b dzie miała rozkład logarytmiczno-normalny. Zauwa my ponadto, e:
)
x
(
g
ln
y
ln
u
t
t
t
−−−−
====
.
(8)
Tym samym zmienna losowa
u
t
, b d c logarytmem zmiennej
v
t
, musi by jednocze nie
ró nic pomi dzy logarytmem zmiennej
y
t
i logarytmem jej składnika systematycznego. Ze
zdefiniowania zmiennych wynika e:
0
u
1
v
)
x
(
g
y
t
t
t
t
<<<<
∧∧∧∧
<<<<
<<<<
,
(9)
0
u
1
v
)
x
(
g
y
t
t
t
t
>>>>
∧∧∧∧
>>>>
>>>>
.
(10)
Na podstawie powy szego powiemy, e zawsze wtedy gdy zmienna obja niana jest mniejsza
od składnika systematycznego, to jej udział w składniku systematycznym jest mniejszy od
jeden a tym samym ró nica logarytmów zmiennej i jej składnika systematycznego jest
ujemna. Z drugiej strony powiemy, e zawsze wtedy gdy zmienna obja niana jest wi ksza od
składnika systematycznego, to jej udział w składniku systematycznym ma warto wi ksz od
jeden a tym samym ró nica logarytmów zmiennej i jej składnika systematycznego jest
dodatnia. Obecnie wyłania si problem zdefiniowania składnika systematycznego w
rozkładzie zmiennej losowej y
t
.
2. SKŁADNIK SYSTEMATYCZNY JAKO WARUNKOWA
REDNIA GEOMETRYCZNA W MODELU MULTIPLIKATYWNYM
Przy formułowaniu wniosków dotycz cych zmiennej losowej
y
t
oraz parametrów jej
rozkładu korzysta b dziemy z nast puj cego twierdzenia:
TWIERDZENIE 1. Je eli logarytm zmiennej losowej y
t
ma rozkład normalny
)
,
(
2
y
ln
y
ln
σσσσ
µµµµ
Ν
Ν
Ν
Ν
to zmienna
y
t
ma rozkład logarytmiczno-normalny
)]
1
e
(
e
,
e
[
2
y
ln
2
y
ln
y
ln
2
2
y
ln
2
1
y
ln
−−−−
Λ
Λ
Λ
Λ
σσσσ
σσσσ
++++
µµµµ
σσσσ
++++
µµµµ
Obecnie załó my, tak jak to si najcz ciej czyni, e zmienna u
t
dla t=1,2,3,...,n ma
rozkład normalny o nast puj cych parametrach:
0
Eu
u
t
====
µµµµ
====
,
(11)

3
.
const
Eu
)
u
(
E
2
u
2
t
2
u
t
====
σσσσ
====
====
µµµµ
−−−−
(12)
W powy szej sytuacji, chc c zdefiniowa parametry zmiennej v
t
, skorzysta mo emy z
nast puj cego twierdzenia, b d cego pochodn Twierdzenia 1:
TWIERDZENIE 2. Je eli w warunkach (7) zmienna losowa u
t
ma rozkład normalny
)
,
0
(
2
u
σσσσ
Ν
Ν
Ν
Ν
,
to
v
t
jest zmienn losow o rozkładzie logarytmiczno-normalnym
)]
1
e
(
e
,
e
[
2
u
2
u
2
u
2
1
−−−−
Λ
Λ
Λ
Λ
σσσσ
σσσσ
σσσσ
Powiemy tym samym, e przy zało eniach (11) i (12) i na mocy Twierdzenia 2 zmienna v
t
ma
rozkład logarytmiczno-normalny o parametrach:
2
u
2
1
v
t
e
Ev
σσσσ
====
µµµµ
====
,
(13)
)
1
e
(
e
)
Ev
v
(
E
2
u
2
u
2
t
t
−−−−
====
−−−−
σσσσ
σσσσ
=
const..
(14)
Z zapisu (5) wynika, i przy przyj tych warunkach logarytm zmiennej
y
t
ma rozkład
normalny i charakteryzuje si nast puj cymi parametrami:
)
x
(
g
ln
b
x
Eu
)
x
(
Eg
y
ln
E
t
t
t
t
t
y
ln
====
====
++++
====
====
µµµµ
,
(15)
.
const
)
x
(
g
y
ln
E
)]
x
(
g
ln
y
[ln
E
)
y
(ln
E
2
t
t
2
t
t
2
y
ln
t
2
y
ln
====
====
−−−−
====
µµµµ
−−−−
====
σσσσ
.
(16)
Poniewa warto oczekiwana logarytmu zmiennej
y jest równa logarytmowi składnika
systematycznego, wi c składnik systematyczny przy przyj tych zało eniach jest warunkow
redni geometryczn zmiennej losowej
y
t
, jako e:
)
t
x
(
g
ln
E
t
y
ln
E
t
e
e
)
x
(
g
====
====
(17)
Z drugiej strony zauwa my, e wariancja logarytmu zmiennej
y
t
jest równa wariancji
zmiennej
u
t
, jako e rozpisuj c wariancj zdefiniowan w (12) otrzymujemy:
.
const
)
x
(
g
y
ln
E
)]
x
(
g
ln
y
[ln
E
Eu
2
t
t
2
t
t
2
t
2
u
====
====
−−−−
====
====
σσσσ
,
(18)
co równa si wyra eniu (16).
Kluczowe znaczenie przy charakteryzowaniu dalszych parametrów rozkładu zmiennej
losowej
y
t
ma Twierdzenie 1. Na jego mocy - po uwzgl dnieniu faktu, i
lny
=lng(x
t
)
[zgodnie z (15)] oraz, e
2
lny
=
2
u
=const [zgodnie z (16) i (18)] - otrzymujemy:
2
u
2
1
t
2
u
2
1
)
t
x
(
g
ln
2
y
ln
2
1
y
ln
t
y
e
)
x
(
g
e
e
e
e
Ey
σσσσ
σσσσ
σσσσ
µµµµ
====
====
====
====
µµµµ
,
(19)
)
1
e
(
e
)
x
(
g
)
1
e
(
e
)
Ey
y
(
E
2
u
2
u
2
t
2
y
ln
2
y
ln
y
ln
2
2
t
t
2
y
−−−−
====
−−−−
====
−−−−
====
σσσσ
σσσσ
σσσσ
σσσσ
σσσσ
++++
µµµµ
. (20)

4
Na podstawie (19) powiemy, e przy zało eniu stałej wariancji zmiennej losowej
u
t
, warto
oczekiwana zmiennej
y
t
zmienia si wraz ze zmian jej redniej geometrycznej. Jest wi c ona
warto ci warunkow . Okre laj c, tak jak to si niekiedy czyni, warto oczekiwan zmiennej
y
t
jako redni arytmetyczn w jej rozkładzie i oznaczaj c t redni symbolem „
a” oraz
uznaj c charakter warunkowy tej redniej, wyra enie (19) zapiszemy w nast puj cy sposób:
2
u
2
1
t
t
e
)
x
(
g
)
x
(
a
σσσσ
====
.
(21)
Wykorzystuj c powy szy zapis, zdefiniowan w (20) wariancj , zapiszemy inaczej jako:
)
1
e
(
)
x
(
a
)]
x
(
a
y
[(
E
2
u
2
t
2
t
t
2
y
−−−−
====
−−−−
====
σσσσ
σσσσ
.
(22)
Na podstawie (22) wyznaczamy odchylenie standardowe zmiennej
y
t
od jej warunkowej
redniej arytmetycznej, co zapiszemy nast puj co:
1
e
)
x
(
a
2
u
t
y
−−−−
====
σσσσ
σσσσ
.
(23)
Z powy szego wynika, e
wariancja zmiennej y
t
, a tym samym odchylenie standardowe
tej zmiennej, ulega zmianie wraz ze zmian jej redniej. Rozproszenie to jest tym
wi ksze, im wi ksza jest warto oczekiwana zmiennej y
t
, która jest ci le uzale niona od
redniej geometrycznej zgodnie z (21).
Poniewa zmienna
y
t
charakteryzuje si rozkładem logarytmiczno-normalny, wi c
warto rodkow (median ) i dominant (mod ) zdefiniujemy nast puj co:
)
x
(
g
e
)
x
(
My
t
y
ln
t
====
====
µµµµ
,
(24
2
u
t
2
y
ln
y
ln
t
e
)
x
(
g
e
)
x
(
Dy
σσσσ
−−−−
σσσσ
−−−−
µµµµ
====
====
.
(25)
Z powy szego wynika, e warunkowa rednia geometryczna zmiennej
y
t
jest
jednocze nie warunkow median tej zmiennej. Ponadto z uwagi na prawostronn asymetri
rozkładu zmiennej
y
t
zachodzi nast puj ca prawidłowo :
)
x
(
a
Ey
)
x
(
g
)
x
(
My
)
x
(
Dy
t
t
t
t
t
====
<<<<
====
<<<<
(26)
Z przeprowadzonych dotychczas rozwa a wynika, e rednia geometryczna w modelu
multiplikatywnym, w którym zmienna obja niana charakteryzuje si rozkładem
logarytmiczno-normalnym, urasta do rangi centralnego parametru rozkładu, jako e
warunkowa warto oczekiwana logarytmu zmiennej y
t
, b d c logarytmem jej redniej
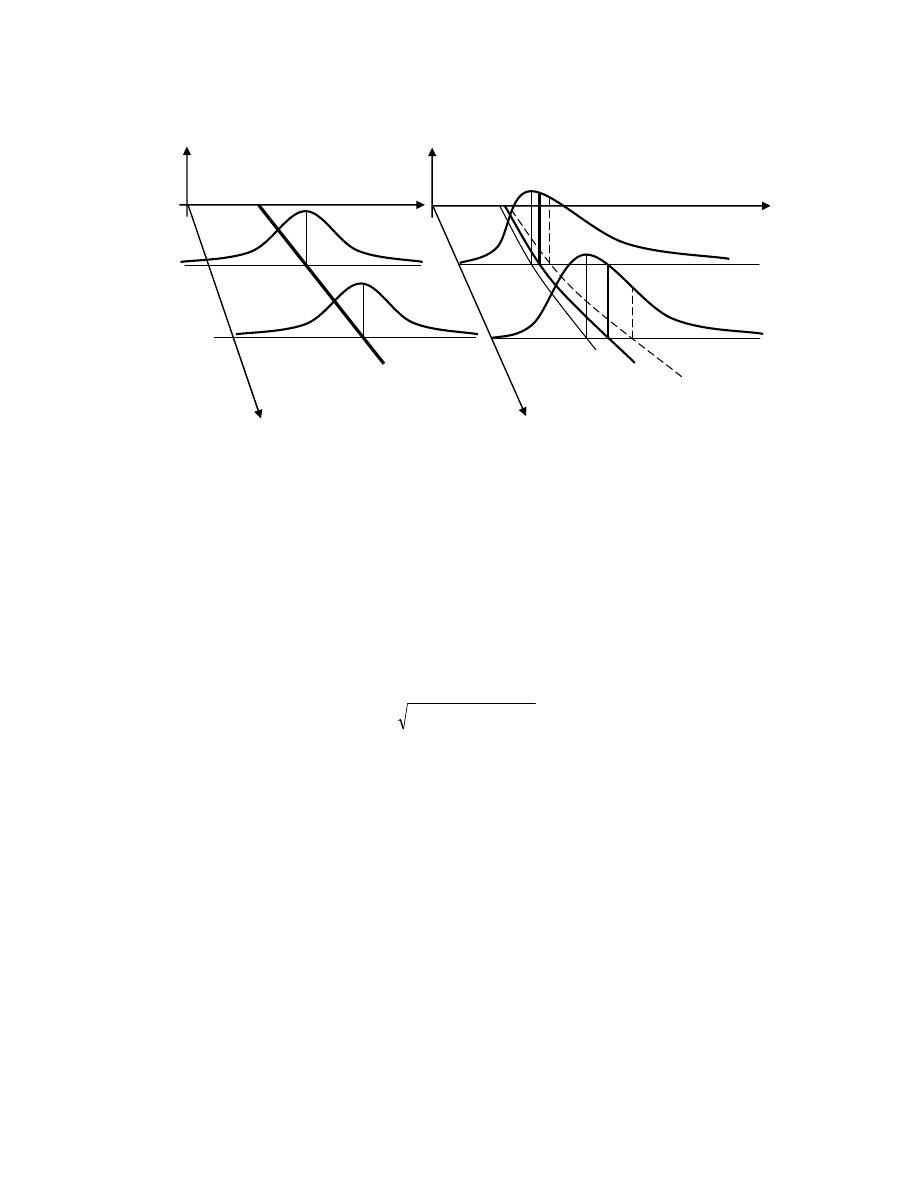
geometrycznej, jest równocze nie logarytmem jej mediany [patrz. rys.1].
Podsumowuj c t cz
rozwa a powiemy, e
je eli zmienna u
t
zdefiniowana przez
(7) i (8) ma rozkład normalny o parametrach okre lonych przez (11) i (12) to:
•
funkcja g(x
t
), b d ca składnikiem systematycznym w modelu (1), jest jednocze nie
warunkow redni geometryczn i median zmiennej obja nianej y
t
,
•
zmienna u
t
wyznacza ró nic pomi dzy logarytmem zmiennej losowej y
t
a
logarytmem jej redniej geometrycznej,
•
zmienna v
t
wyznacza stosunek zmiennej y
t
do jej redniej geometrycznej.
5
Ko cz c t cz
rozwa a zauwa my, e umiemy zdefiniowa miar przeci tnego
rozproszenia logarytmu zmiennej
y
t
w relacji do logarytmu jej warunkowej redniej
geometrycznej. Miar tego rozproszenia jest bowiem odchylenie standardowe, b d ce
dodatnim pierwiastkiem wariancji zmiennej
u
t
zdefiniowanej w (12) i (18). Jest ono
równocze nie dodatnim pierwiastkiem wariancji logarytmu zmiennej
y
t
wzgl dem logarytmu
jej redniej geometrycznej zdefiniowanej w (16), co zapiszemy nast puj co:
2
t
t
u
)]
x
(
g
ln
y
[ln
E
−−−−
====
σσσσ
.
(27)
Odchylenie to jest wyra one w logarytmach zmiennej y. Jest wi c miar niemianowan i tym
samym trudn do zinterpretowania. Nie my limy bowiem w kategoriach logarytmów, chocia
mo emy rozumie ich istot . W tej sytuacji zarysowuje si potrzeba zdefiniowania i
zinterpretowania odpowiedniej miary rozproszenia zmiennej y
t
w relacji do jej redniej
geometrycznej.
3. WZGL DNE I ABSOLUTNE ROZPROSZENIE ZMIENNEJ OBJA NIANEJ
W RELACJI DO JEJ WARUNKOWEJ REDNIEJ GEOMETRYCZNEJ
Przyj te zało enia o rozkładzie normalnym zmiennej
u
t
, a tym samym o rozkładzie
normalnym logarytmu zmiennej obja nianej, upowa niaj nas do nast puj cej konstatacji:
prawdopodobie stwo tego, i logarytm zmiennej y
t
przyjmie warto ró ni c si od
logarytmu jej redniej geometrycznej o jedno odchylenie standardowe, jest równe
0,6826, co jest zgodne z reguł trzech sigm. Prawidłowo t zapiszemy nast puj co:
6826
,
0
)
)
x
(
g
ln
y
ln
(
P
u
t
t
u
====
σσσσ
<<<<
−−−−
<<<<
σσσσ
−−−−
,
(28)
lub w równowa nej postaci:
Rys. 1 Obraz graficzny modelu multiplikatywnego w wersji pierwotnej
i zlinearyzowanej – przypadek modelu wykładniczego:
y
t
=g(x
t
)v
t
ln y
t
=lng(x
t
)+u
t
,
gdzie: g(x
t
)=exp(b
0
+b
1
x
t1
) lng(x
t
)=b
0
+b
1
x
t
,
u
t
= lnv
t
, u
t
~ N(0,
2
u
)
f(lny
t
)
f(y
t
)
lny
t
y
t
x
1
x
1
x
2
x
2
Elny
t
=lng(x
t
)
My(x
t
)
Dy(x
t
)
Ey(x
t
)
gdzie: My(x
t
) = g(x
t
)
Ey(x
t
) = g(x
t
)exp(0,5
2
u
)
Dy(x
t
) = g(x
t
)exp(-
2
u
)
x
t
x
t

6
6826
,
0
)
)
x
(
g
y
ln
(
P
u
t
t
u
====
σσσσ
<<<<
<<<<
σσσσ
−−−−
.
(29)
Celem wzbogacenia interpretacji otrzymanych wyników zdelogarytmujmy stronami
wyra enie w nawiasie. W wyniku tego działania otrzymujemy:
6826
,
0
)
e
)
x
(
g
y
e
(
P
u
t
t
u
====
<<<<
<<<<
σσσσ
σσσσ
−−−−
,
(30)
co po przyj ciu nast puj cych oznacze :
1
e
v
0
u
d
<<<<
====
<<<<
σσσσ
−−−−
,
(31)
1
e
v
u
g
>>>>
====
σσσσ
(32)
oraz wykorzystaniu zdefiniowania zmiennej v
t
w (4) pozwala przedstawi (30) w postaci:
6826
,
0
)
v
v
v
(
P
g
t
d
====
<<<<
<<<<
.
(33)
Przed wykorzystaniem wyra enia (33) dla celów interpretacyjnych zauwa my, e:
1
e
e
e
v
v
0
y
ln
y
ln
g
d
====
====
====
⋅⋅⋅⋅
σσσσ
σσσσ
−−−−
(34)
Powy sza wła ciwo jest o tyle istotna, i rednia geometryczna zmiennej v
t
jest równa
jedno ci, co wynika z nast puj cego faktu:
1
e
e
e
g
0
)]
x
(
g
ln
y
[ln
E
Eu
0
)]
t
x
(
g
ln
t
y
[ln
E
t
v
ln
E
v
t
t
t
====
====
====
====
====
−−−−
====
−−−−
(35)
gdzie
g
v
=1 jest redni geometryczn zmiennej v
t
dla
t=1,2,3,...,n.
Obecnie na podstawie (33) powiemy, e
z prawdopodobie stwem równym 0,6826
udział zmiennej losowej y
t
w jej warunkowej redniej geometrycznej g(x
t
) mie ci si
b dzie w przedziale od v
d
do v
g
. Oznacza to, e dokonuj c interpretacji w my l której,
przeci tny udział zmiennej y
t
w jej redniej geometrycznej waha si w granicach od v
d
do v
g
mamy na my li fakt, i jest to przeci tny udział w kategoriach standardowych, gdy
został on wyznaczony na bazie odchylenia standardowego logarytmu zmiennej
y
t
z wszelkimi
wypływaj cymi z tego konsekwencjami stochastycznymi. Powiemy tym samym, e
v
d
i v
g
s
przeci tnymi, wzgl dnymi miarami rozproszenia zmiennej losowej y
t
wzgl dem jej
warunkowej redniej geometrycznej.
Celem dalszego wzbogacenia interpretacji omawianej przez nas
wzgl dnej miary
rozproszenia, dokonajmy przekształcenia nierówno ci równoczesnej uj tej w (33) poprzez
odj cie stronami warto ci 1. W rezultacie tego działania otrzymujemy:
6826
,
0
)
1
v
1
)
x
(
g
y
1
v
(
P
g
t
t
d
====
−−−−
≤≤≤≤
−−−−
≤≤≤≤
−−−−
(36)
Przemna aj c powy sz nierówno stronami przez 100, otrzymany wynik wyra amy w
procentach, co zapiszemy nast puj co:
6826
,
0
]
100
)
1
v
(
100
)
)
x
(
g
)
x
(
g
y
(
100
)
1
v
[(
P
g
t
t
t
d
====
−−−−
≤≤≤≤
−−−−
≤≤≤≤
−−−−
(37)
Obecnie powiemy, e w sensie standardowym przeci tnie, zmienna losowa
y
t
odchyla si od
jej redniej geometrycznej w przedziale od
(v
d
-1)100% do (v
g
-1)100%. W analizowanym

7
przypadku odchylenia te b d zawiera si w wyznaczonych granicach dla 2/3 wszystkich
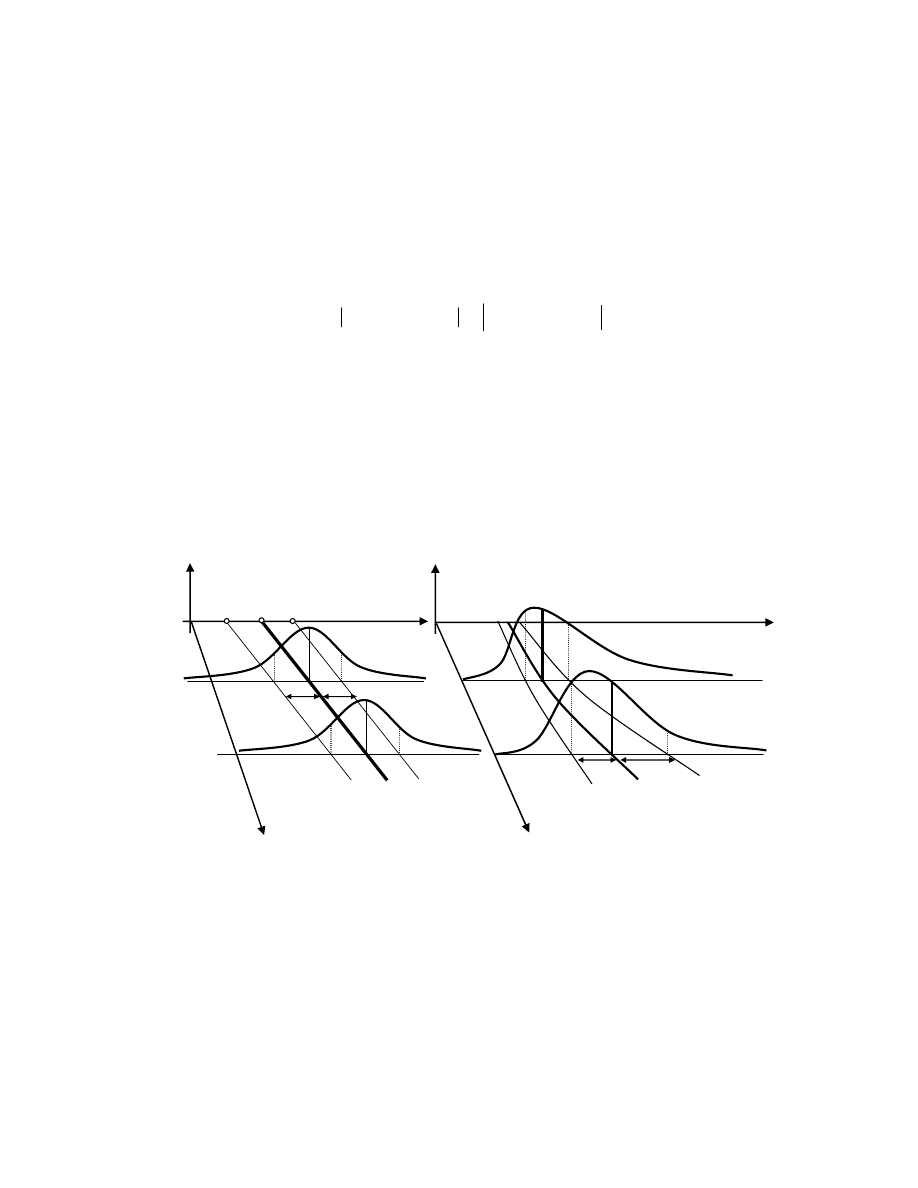
przypadków. Omówion powy ej sytuacj w uj ciu graficznym przedstawiono na
rys.2.
Mo na obecnie zada pytanie: dlaczego wyznaczamy dolne i górne przedziały
przeci tnych odchyle , zamiast powiedzie wprost, o ile procent przeci tnie zmienna
y
odchyla si od jej redniej geometrycznej? Odpowied wynika z asymetrii rozkładu
logarytmiczno-normalnego. Mo na bowiem udowodni , rozpisuj c w szereg pot gowy
wyra enia (31) i (32), i spełnione s nast puj ce nierówno ci:
1
v
v
1
0
)
1
v
(
)
1
v
(
g
d
g
d
−−−−
<<<<
−−−−
⇔
⇔
⇔
⇔
>>>>
−−−−
++++
−−−−
.
(38)
Nie mo na wi c w analizowanym przypadku zdefiniowa jednoparametrycznej miary
przeci tnego, wzgl dnego rozproszenia zmiennej
y
t
w relacji do jej redniej geometrycznej.
Rozproszenie to z uwagi na wyst puj c asymetri odległo ci od warto ci redniej uj
musimy za pomoc dwu parametrów zmiennej
v
t
.
Zastanówmy si obecnie nad absolutnym rozproszeniem zmiennej
y
t
w relacji do jej
redniej geometrycznej. Celem jego wyznaczenia przemnó my stronami nierówno
równoczesn zawart w nawiasie wyra enia (29) przez wielko
g(x
t
). Po przyj ciu
dodatkowo oznacze (31) i (32) ostatecznie otrzymujemy:
6826
,
0
]
v
)
x
(
g
y
v
)
x
(
g
[
P
g
t
t
d
t
=
⋅
≤
≤
⋅
.
(39)
Obecnie powiemy, e
prawdopodobie stwo tego, i zmienna losowa y
t
przyjmuje
warto ci w granicach od g(x
t
)·v
d
do g(x
t
)·v
g
, jest równe 0,6826. Nale y podkre li , e
zarówno zmienna losowa
y
t
jak i wyznaczone granice prawdopodobie stw wyra one s w
jednostkach rzeczywistych analizowanej zmiennej. Aby wyja ni istot asymetrii
Rys. 2 Obraz graficzny rozproszenia wzgl dnego zmiennej obja nianej wzgl dem jej
redniej geometrycznej w modelu multiplikatywnym w wersji pierwotnej i zlinearyzowanej
– przypadek modelu wykładniczego:
v
t
=y
t
/g(x
t
)
u
t
=ln y
t
-lng(x
t
),
gdzie: g(x
t
)=exp(b
0
+b
1
x
t1
) lng(x
t
)=b
0
+b
1
x
t
,
u
t
= lnv
t
, u
t
~ N(0,
2
u
)
f(u
t
)= f(lnv
t
)
f(v
t
)
lny
t
v
t
x
1
x
1
x
2
x
2
Eu
t
=Elnv
t
=0
expEu
t
=1
gdzie: v
d
= exp-
u
< 1
v
g
= exp
u
> 1
v
d
·v
g
= 1
x
t
u
u
-
u
u
v
d
v
g
0
8
wyznaczonej tutaj absolutnej miary rozproszenia zauwa my, e poniewa logarytm zmiennej
y
t
ma rozkład normalny, wi c spełniona musi by nast puj ca równo :
)]
x
(
g
y
ln
)
x
(
g
[
P
t
t
u
t
d
≤≤≤≤
≤≤≤≤
σσσσ
−−−−
=
341
,
0
]
)
x
(
g
y
ln
)
x
(
g
[
P
u
t
t
t
g
====
σσσσ
++++
≤≤≤≤
≤≤≤≤
,
(40)
co po zdelogarytmowaniu wyra e ograniczonych nawiasami i przyj ciu wcze niej
przyj tych oznacze zapiszemy nast puj co:
341
,
0
]
v
)
x
(
g
y
)
x
(
g
[
P
)]
x
(
g
y
v
)
x
(
g
[
P
g
t
t
t
g
t
t
d
t
d
====
⋅⋅⋅⋅
≤≤≤≤
≤≤≤≤
====
≤≤≤≤
≤≤≤≤
⋅⋅⋅⋅
.
(41)
Z uwagi na (38) stwierdzamy, e:
g
t
t
t
d
t
v
)
x
(
g
)
x
(
g
)
x
(
g
v
)
x
(
g
⋅⋅⋅⋅
−−−−
<<<<
−−−−
⋅⋅⋅⋅
(42)
Oznacza to, e analizowane absolutne rozproszenie zmiennej
y
t
odnosi si do jej warunkowej
redniej geometrycznej (mediany). Rozproszenie to charakteryzuje si tym,
i jednakowemu
prawdopodobie stwu realizacji zdarze odpowiada, co do warto ci bezwzgl dnej,
mniejszy przedział dolny i wi kszy przedział górny odchyle zmiennej y
t
od jej redniej
geometrycznej (mediany). Obecnie mo emy powiedzie , e przeci tne, w sensie
standardowym, odchylenie zmiennej losowej y
t
od jej redniej geometrycznej (mediany)
waha si w granicach od g(x
t
)·v
d
do g(x
t
)·v
g
. Jest to, jak si wydaje, w miar poprawny
sposób okre lenia przeci tnej, absolutnej miary rozproszenia zmiennej losowej
y
t
w stosunku
do jej warto ci redniej w sytuacji, gdy zmienna ta charakteryzuje si asymetrycznym
rozkładem. Omówion powy ej sytuacj w uj ciu graficznym przedstawiono na
rys.3.
Rys.3 Obraz graficzny rozproszenia absolutnego zmiennej obja nianej wzgl dem jej
redniej geometrycznej w modelu multiplikatywnym w wersji pierwotnej i zlinearyzowanej
– przypadek modelu wykładniczego:
y
t
=g(x
t
)v
t
ln y
t
=lng(x
t
)+u
t
,
gdzie: g(x
t
)=exp(b
0
+b
1
x
t1
) lng(x
t
)=b
0
+b
1
x
t
,
u
t
= lnv
t
, u
t
~ N(0,
2
u
)
f(lny
t
)
f(y
t
)
lny
t
y
t
x
1
x
1
x
2
x
2
Elny
t
=lng(x
t
)
g(x
t
)
gdzie: My(x
t
) = g(x
t
) = expElny
t
v
d
= exp-
u
< 1
v
g
= exp
u
> 1
x
t
x
t
u
u
lng(x
t
)-
u
lng(x
t
) lng(x
t
)+
u
g(x
t
)·v
d
g(x
t
)·v
g

9
4. HETEROSCEDASTYCZNO W MODELU MULTIPLIKATYWNYM
Z zapisu (20) wynika, e wariancja zmiennej
y
t
wzgl dem jej redniej arytmetycznej
jest niestała i zale y od poziomu jej warunkowej redniej geometrycznej a tym samym od
poziomu sprz onej z ni redniej arytmetycznej. Rozproszenie to mierzone odchyleniem
standardowym zdefiniowanym w (23) w sensie odległo ci od warunkowej redniej
arytmetycznej jest symetryczne. Mo na jednak wykaza , e asymetria rozkładu zmiennej
y
t
prowadzi do tego, i
jednakowemu rozproszeniu absolutnemu i wzgl dnemu zmiennej
losowej y
t
w relacji do redniej arytmetycznej a(x
t
) odpowiada wi ksze
prawdopodobie stwo odchyle ujemnych oraz mniejsze prawdopodobie stwo odchyle
dodatnich.
Aby wyja ni problem niestało ci rozproszenia zmiennej
y
t
wzgl dem jej redniej
geometrycznej i sposobu interpretacji tego rozproszenia, przekształ my (41) odejmuj c
stronami od wyra e zawartych w nawiasach wielko
g(x
t
). W ten sposób otrzymujemy:
341
,
0
)]
x
(
g
v
)
x
(
g
)
x
(
g
y
0
[
P
)]
0
)
x
(
g
y
)
x
(
g
v
)
x
(
g
[
P
t
g
t
t
t
g
t
t
t
d
t
d
====
−−−−
⋅⋅⋅⋅
≤≤≤≤
−−−−
≤≤≤≤
====
≤≤≤≤
−−−−
≤≤≤≤
−−−−
⋅⋅⋅⋅
,
co ostatecznie zapiszemy nast puj co:
341
,
0
))]
1
v
)(
x
(
g
0
[
P
)]
0
))
1
v
)(
x
(
g
[
P
g
t
t
g
t
d
t
d
====
−−−−
≤≤≤≤
εεεε
≤≤≤≤
====
≤≤≤≤
εεεε
≤≤≤≤
−−−−
,
(43)
gdzie:
)
x
(
g
y
t
t
t
−−−−
====
εεεε
.
(44)
Zmienna losowa
t
jest zdefiniowana jako ró nica pomi dzy zmienn
y
t
a jej redni
geometryczn . Z (43) wynika, e
przedział dolny i górny odchyle zmiennej y
t
od jej
warunkowej redniej geometrycznej wzrasta wraz ze wzrostem redniej geometrycznej
oraz maleje wraz ze spadkiem tej redniej. Jednocze nie prawdopodobie stwo odchyle
dolnych jest równe prawdopodobie stwu odchyle górnych przy jednoczesnym zachowaniu
warunku sformułowanego w (42). Wskazuje to na specyficzny sposób okre lenia
heteroscedastyczno ci wariancji zmiennej
y
t
wzgl dem jej redniej geometrycznej.
Na marginesie prowadzonych tutaj rozwa a zauwa my, e na podstawie (44) model
o postaci (1) przedstawi mo emy w nast puj cej równowa nej postaci z addytywnym
składnikiem zakłócaj cym:
t
t
t
)
x
(
g
y
εεεε
++++
====
,
(45)
gdzie z uwagi na fakt, i zmienna obja niana i jej składnik systematyczny przyjmuj jedynie
warto ci dodatnie spełniony musi by nast puj cy warunek:
]
1
v
)[
x
(
g
t
t
t
0
t
v
−−−−
====
εεεε
Λ
Λ
Λ
Λ
>>>>
.
(46)
Dla dora nych celów analitycznych warto wykaza , e:
]
1
e
2
e
[
)
x
(
g
)]
x
(
g
y
[
E
2
u
2
1
2
u
2
2
2
t
t
++++
−−−−
====
−−−−
σσσσ
σσσσ
(47)
Powy ej zdefiniowana miara rozproszenia zmiennej
y
t
ma charakter hybrydy. Wskazuje ona
bowiem na rednie - w sensie arytmetycznym - kwadratowe odchylenie zmiennej losowej
y
t
od jej redniej geometrycznej. Jest wi c ona miar mieszan i nie jest tym samym
metodologicznie koherentn . Mimo tej niedoskonało ci metodologicznej, na jej podstawie
wygodnie jest odczyta niestało (heteroscedastyczno ) wariancji zmiennej
y
t
wzgl dem
redniej geometrycznej. Analizuj c (47) stwierdzamy, e im wi kszy jest poziom redniej

10
geometrycznej zmiennej obja nianej tym wi ksza jest - w ten nietypowy sposób obliczona –
wariancja zmiennej
y
t
.
5. ESTYMATOR MNK REDNIEJ GEOMETRYCZNEJ ZMIENNEJ OBJA NIANEJ
Celem sformułowania wniosków dotycz cych wła ciwo ci estymatora warunkowej
redniej geometrycznej zmiennej y
t
wygodnie jest zapisa model (5) w równowa nej dla
niego postaci macierzowej:
u
Xb
y
*
++++
====
(48)
gdzie:
]
y
ln
...
y
ln
y
[ln
'
y
n
2
1
*
====
- transponowany wektor kolumnowy logarytmów warto ci
obserwowanych zmiennej obja nianej,
)
1
k
(
n
X
++++
××××
- macierz obserwowanych warto ci zmiennych obja niaj cych,
]
u
...
u
u
u
[
'
u
n
3
2
1
====
- transponowany wektor kolumnowy składników losowych
zdefiniowanych w (7), tym samym
]
v
ln
...
v
ln
v
[ln
u
n
2
1
T
====
.
Załó my ponadto, e spełniony jest zbiór nast puj cych zało e :
n
1
k
)
X
(
r
<<<<
++++
====
,
(49)
)
I
,
0
(
~
u
n
2
u
σσσσ
Ν
Ν
Ν
Ν
.
(50)
Rozwa my obecnie estymator logarytmu zmiennej
y
t
o postaci:
bˆ
x
yˆ
ln
t
t
====
,
(51)
gdzie:
*
1
y
'
X
)
X
'
X
(
bˆ
−−−−
====
.
(52)
Posta zdelogarytmowana estymatora (51) przedstawia si nast puj co:
bˆ
t
x
t
e
yˆ ====
.
(53)
Zauwa my, e wykorzystuj c estymator (51) wyznaczy mo emy warto ci teoretyczne
logarytmów zmiennej obja nianej. Natomiast estymator (53) umo liwia oszacowanie warto ci
teoretycznych zmiennej obja nianej w jej pierwotnej postaci. Z drugiej strony wiemy, e
zdefiniowany w (52) estymator MNK parametrów strukturalnych rozpatrywanego modelu
otrzymali my minimalizuj c nast puj c form kwadratow :
====
====
====
−−−−
====
n
1
t
n
1
t
2
t
t
2
t
t
yˆ
y
ln
)
yˆ
ln
y
(ln
S
(54)
Powiemy wi c, e estymator (52) zapewnia minimum sumy kwadratów odległo ci
zlogarytmowanych warto ci zmiennej obja nianej od zlogarytmowanych warto ci
teoretycznych tej e zmiennej. Tym samym zapewnia minimum sumy kwadratów logarytmu
udziału warto ci rzeczywistych zmiennej obja nianej w warto ciach teoretycznych tej
zmiennej. W wietle powy szego powstaj pytania dotycz ce wła ciwo ci estymatorów
zmiennej obja nianej w jej zlogarytmowanej i pierwotnej formie oraz istoty zastosowanego
kryterium estymacji.

11
Na wst pie zauwa my, e z uwagi na zało enia sformułowane w (49) i (50) wykaza
mo emy, e estymator parametrów strukturalnych modelu (52) charakteryzuje si
wielowymiarowym rozkładem normalnym o nast puj cych parametrach:
b
bˆ
E ====
,
(55)
1
T
2
u
T
)
X
X
(
)
b
bˆ
)(
b
bˆ
(
E
)
bˆ
(
−−−−
σσσσ
====
−−−−
−−−−
====
ΣΣΣΣ
,
(56)
gdzie estymator (56) jest macierz kowariancji estymatorów parametrów strukturalnych
modelu. Ponadto z uwagi na fakt, i estymator
bˆ
ma rozkład normalny, wi c zdefiniowany w
(49) estymator
t
yˆ
ln
ma rozkład normalny. W konsekwencji opisany przez (53) estymator
t
yˆ
ma rozkład logarytmiczno-normalny. Uwzgl dniaj c (55) stwierdzamy, e warto
oczekiwana logarytmu estymatora
t
yˆ
zdefiniowanego w (51) jest równa warto ci
oczekiwanej logarytmu zmiennej
y
t
zdefiniowanej w (5), jako e
)
x
(
g
ln
b
x
bˆ
E
x
)
bˆ
x
(
E
yˆ
ln
E
t
t
t
t
t
====
====
====
====
,
(57)
W tych warunkach rednia geometryczna estymatora sformułowanego w (53) jest równa
redniej geometrycznej zmiennej losowej
y
t
opisanej przez model (1), jako e:
t
y
ln
E
t
yˆ
ln
E
t
e
e
)
x
(
g
====
====
Podsumowuj c powiemy, e
w warunkach przyj tych zało e dla modelu
multiplikatywnego:
•
zmienna obja niana i jej estymator klasy MNK maj rozkład logarytmiczno-
normalny,
•
rednia geometryczna zmiennej obja nianej jest równa redniej geometrycznej jej
estymatora klasy MNK.
6. OCENY ZAKŁÓCE LOSOWYCH W MODELU MULTIPLIKATYWNYM
Rozwa my obecnie oceny wyró nionych form składnika zakłócaj cego w modelu
multiplikatywnym. Oceny te zdefiniujemy nast puj co:
t
t
t
yˆ
y
vˆ ====
,
(58)
t
t
t
t
t
t
vˆ
ln
yˆ
y
ln
yˆ
ln
y
ln
uˆ
====
====
−−−−
====
,
(59)
]
1
vˆ
[
yˆ
yˆ
y
ˆ
t
t
t
t
t
−−−−
====
−−−−
====
εεεε
.
(60)
Na podstawie (58) powiemy, e:
•
ocena zakłócenia w postaci
t
vˆ
wskazuje na udział warto ci rzeczywistych zmiennej
obja nianej modelu w warto ciach teoretycznych tej zmiennej ustalonych na
poziomie redniej geometrycznej,
•
ocena zakłócenia w postaci
t
uˆ
wskazuje na ró nic logarytmów warto ci
rzeczywistych zmiennej obja nianej modelu od logarytmu warto ci teoretycznych tej
zmiennej ustalonych na poziomie redniej geometrycznej, a tym samym okre la
logarytm udziału warto ci rzeczywistych zmiennej obja nianej modelu w
warto ciach teoretycznych tej zmiennej ustalonych na poziomie redniej
geometrycznej,
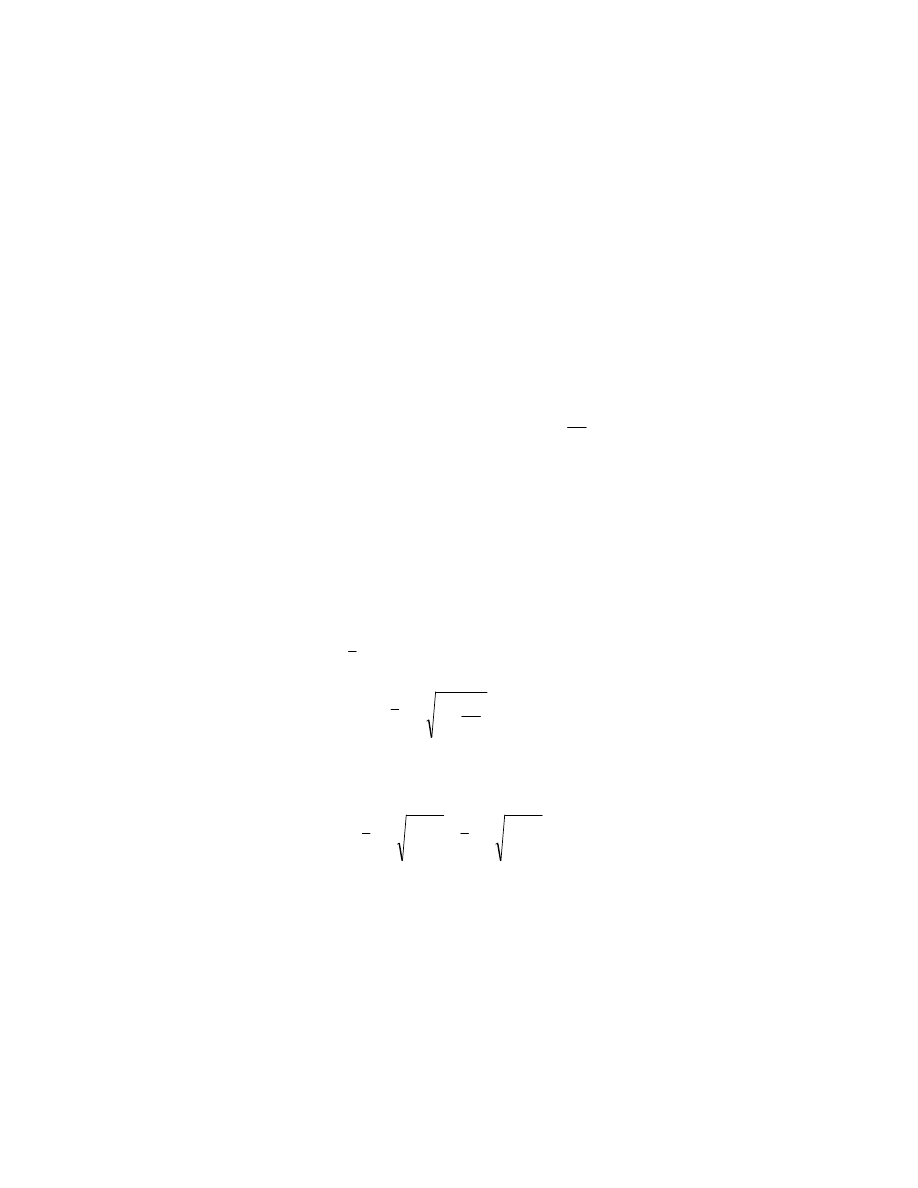
12
•
ocena zakłócenia w postaci
t
ˆεεεε
wskazuje na ró nic warto ci rzeczywistych zmiennej
obja nianej modelu od warto ci teoretycznych tej zmiennej ustalonych na poziomie
redniej geometrycznej.
Przy okazji zauwa my, e
0
uˆ
1
vˆ
yˆ
y
t
t
t
t
<<<<
∧∧∧∧
<<<<
<<<<
,
(61)
0
uˆ
1
vˆ
yˆ
y
t
t
t
t
>>>>
∧∧∧∧
>>>>
>>>>
.
(62)
Na podstawie powy szego powiemy, e zawsze wtedy gdy zmienna obja niana jest mniejsza
od jej warto ci teoretycznej, to jej udział w warto ci teoretycznej jest mniejszy od jeden a tym
samym ró nica logarytmów zmiennej i jej warto ci teoretycznej jest ujemna. Z drugiej strony
powiemy, e zawsze wtedy gdy zmienna obja niana jest wi ksza od jej warto ci teoretycznej,
to jej udział w warto ci teoretycznej ma warto wi ksz od jeden a tym samym ró nica
logarytmów zmiennej i jej warto ci teoretycznej jest dodatnia.
Z wła ciwo ci numerycznych estymatora MNK wynika ponadto, e
∏
∏
∏
∏
∏
∏
∏
∏
====
====
====
====
====
====
====
====
n
1
t
n
1
t
t
t
t
n
1
t
n
1
t
t
t
1
)
yˆ
y
(
vˆ
0
vˆ
ln
uˆ
,
(63)
∏
∏
∏
∏
∏
∏
∏
∏
====
====
====
====
====
====
n
1
t
n
1
t
t
t
n
1
t
n
1
t
t
t
yˆ
y
yˆ
ln
y
ln
.
(64)
Tym samym stosuj c estymator MNK dla zlinearyzowanej postaci modelu multiplikatywnego
przy wykorzystaniu próby statystycznej spełniaj cej warunek (49) stwierdzamy, i :
•
iloczyn udziału warto ci rzeczywistych w warto ciach teoretycznych jest równy
jedno ci,
•
iloczyn warto ci rzeczywistych jest równy iloczynowi warto ci teoretycznych.
Oznacza to, i
•
rednia geometryczna
vˆ
g
relacji zmiennej
y
t
do jej warto ci teoretycznej jest równa
jedno ci, tzn.:
1
)
yˆ
y
(
g
n
n
1
t
t
t
vˆ
====
====
∏
∏
∏
∏
====
,
(65)
•
rednia geometryczna obserwowanych warto ci zmiennych obja nianych (
y
t
) oraz
rednia geometryczna warto ci teoretycznych (
t
yˆ
) s sobie równe, tzn.:
n
n
1
t
t
yˆ
n
n
1
t
t
y
yˆ
g
y
g
∏
∏
∏
∏
∏
∏
∏
∏
====
====
====
≡≡≡≡
====
.
(66)
7. OCENA I INTERPRETACJA PRZECI TNEGO WZGL DNEGO
ROZPROSZENIA ZMIENNEJ OBJA NIANEJ W RELACJI DO ESTYMATORA
REDNIEJ GEOMETRYCZNEJ
Z uwagi na fakt, e zdefiniowane w (58), (59) i (60) formy ocen zakłóce modelu
multiplikatywnego s funkcjami zmiennej losowej
y
t
, uzna je nale y za estymatory
odpowiednich zmiennych losowych
u
t
, v
t
i
t
. W wietle przyj tych zało e powiemy, i
estymator:
•
t
vˆ
charakteryzuje si rozkładem logarytmiczno-normalnym,

13
•
t
uˆ
charakteryzuje si rozkładem normalnym,
•
t
ˆεεεε
charakteryzuj si rozkładem logarytmiczno-normalnym przesuni tym.
Obecnie przy przyj tych zało eniach stwierdzamy, i
1
e
e
e
g
0
)]
yˆ
ln
y
[ln
E
uˆ
E
0
)]
t
yˆ
ln
t
y
[ln
E
t
vˆ
ln
E
v
t
t
t
====
====
====
====
====
−−−−
====
−−−−
(67)
Porównuj c (67) z (35) powiemy, e przy przyj tych zało eniach, dla ka dego t=1,2,..,n:
•
warto oczekiwana ( rednia arytmetyczna) zmiennej
t
uˆ
jest równa warto ci oczekiwanej
( redniej arytmetycznej) zmiennej losowej
u
t
, tym samym rozpatrywany estymator reszt
jest nieobci ony,
•
rednia geometryczna zmiennej
t
vˆ
jest równa redniej geometrycznej zmiennej losowej
v
t
i tylko w takim sensie mo emy mówi o nieobci ono ci rozpatrywanego estymatora
losowego zakłócenia multiplikatywnego w rozpatrywanym modelu multiplikatywnym.
Wykorzystuj c reszty postaci logarytmowanej modelu multiplikatywnego definiujemy
wariancj resztow w nast puj cy sposób:
)
1
k
(
n
)
vˆ
(ln
)
1
k
(
n
)
yˆ
ln
y
(ln
)
1
k
(
n
uˆ
ˆ
n
1
t
2
t
n
1
t
2
t
t
n
1
t
2
t
2
u
++++
−−−−
====
++++
−−−−
−−−−
====
++++
−−−−
====
σσσσ
====
====
====
(68)
Powy ej zdefiniowana wariancja resztowa wyznacza rednie kwadratowe odchylenie
logarytmu zmiennej losowej
y
t
od logarytmu jej warto ci teoretycznych, czyli od logarytmu
warunkowych rednich geometrycznych oszacowanych na podstawie próby statystycznej.
Wariancja ta jest ci le zwi zana z kryterium estymacji sformułowanym w (54). Jednocze nie
wykaza mo emy, e przy przyj tych zało eniach wariancja resztowa zdefiniowana w (68)
jest nieobci onym estymatorem wariancji zmiennej losowej
u
t
zdefiniowanej w (18), a tym
samym jest nieobci onym estymatorem wariancji zmiennej losowej
y
t
zdefiniowanej w (16),
co oznacza, e:
2
y
2
u
2
u
ˆ
E
σσσσ
====
σσσσ
====
σσσσ
(69).
Na podstawie (68) szacujemy odchylenie standardowe reszt, b d ce dodatnim pierwiastkiem
wariancji resztowej, co zapisujemy nast puj co:
2
1
t
2
t
t
u
)
1
k
(
n
)
yˆ
ln
y
(ln
ˆ
++++
−−−−
−−−−
====
σσσσ
====
,
(70)
Zapisane powy ej odchylenie standardowe reszt jest punktow ocen zdefiniowanego w (28)
odchylenia standardowego. Jest ono tym samym miar przeci tnego rozproszenia logarytmów
obserwowanych warto ci zmiennej obja nianej w stosunku do logarytmów warto ci
teoretycznych b d cych ocenami warunkowych rednich geometrycznych zmiennej
obja nianej z próby statystycznej. Podobnie jak (27) jest ono miar wyra on w logarytmach i
tym samym trudn do zinterpretowania. Dla celów interpretacyjnych zdefiniowane w (70)
odchylenie standardowe reszt wykorzysta mo emy przy wyznaczaniu ocen zdefiniowanych
w (31) i (32) wielko ci
v
d
i
v
g
b d cych przeci tnymi, wzgl dnymi miarami rozproszenia
zmiennej losowej
y
t
w relacji do jej warunkowej redniej geometrycznej. W rezultacie
wprowadzaj c w wyra eniach (31) i (32) w miejsce odchylenia standardowego
u
jego ocen
punktow zdefiniowan w (70) otrzymujemy odpowiednio:
u
ˆ
d
e
v
σσσσ
−−−−
====
,
(71)

14
u
ˆ
g
e
v
σ
=
.
(72)
Obecnie powiemy, e
w sensie standardowym przeci tny udział warto ci rzeczywistych
(obserwowanych) zmiennej y
t
w warto ciach teoretycznych modelu multiplikatywnego
waha si w granicach od
d
v
do
g
v
. Zauwa my, e podobnie jak w (34) mamy
1
e
e
e
v
v
0
y
ln
ˆ
y
ln
ˆ
g
d
====
====
====
⋅⋅⋅⋅
σσσσ
σσσσ
−−−−
.
(73)
Bior c pod uwag powy sze oraz wykazan w (65) wła ciwo numeryczn rozpatrywanego
estymatora stwierdzamy, e analizowana miara wzgl dnego rozproszenia obserwowanych
warto ci zmiennej obja nianej w relacji do warto ci teoretycznych jest równoznaczna
wzgl dnej mierze rozproszenia tych e relacji w stosunku do ich redniej geometrycznej
równej jedno ci. Zauwa my ponadto, e podobnie jak w (38), spełnione s nast puj ce
nierówno ci:
1
v
v
1
0
)
1
v
(
)
1
v
(
g
d
g
d
−−−−
<<<<
−−−−
⇔
⇔
⇔
⇔
>>>>
−−−−
++++
−−−−
,
(74)
co wiadczy, e w przypadku modelu multiplikatywnego nie potrafimy wyznaczy dokładnej
jednoparametrycznej oceny miary przeci tnego, wzgl dnego rozproszenia obserwowanych
warto ci zmiennej obja nianej w relacji do warto ci teoretycznych. Wynika to z asymetrii
rozkładu estymatora zmiennej obja nianej w modelu multiplikatywnym, jako e estymator ten
ma rozkład logarytmiczno-normalny.
Poniewa wielko ci miar
d
v
i
g
v
w sensie numerycznym wynikaj z kryterium (54)
powiemy, e
estymator MNK zastosowany dla zlinearyzowanej postaci modelu
multiplikatywnego zapewnia najmniejsze wzgl dne rozproszenie zmiennej obja nianej
w relacji do warto ci teoretycznych w tym sensie, e ró nica:
d
g
v
v
)
v
(
disp
−−−−
====
(75)
jest najmniejsza. Ka dy inny estymator zastosowany do modelu multiplikatywnego jest
gorszy w sensie ró nicy (75). Tym samym
oceny otrzymane na podstawie ka dego innego
estymatora prowadz do wi kszej ró nicy charakteryzuj cej wzgl dne rozproszenie
obserwowanych warto ci zmiennej obja nianej w relacji do jej warto ci teoretycznych.
Ko cz c t cz
rozwa a zauwa my, e wyra enie:
1
T
2
u
)
X
X
(
ˆ
)
bˆ
(
ˆ
−−−−
σσσσ
====
ΣΣΣΣ
(76)
jest nieobci onym estymatorem macierzy wariancji i kowariancji estymatorów parametrów
strukturalnych modelu zdefiniowanej w (56).
8. KURS DOLARA AMERYKA SKIEGO A POZIOM CEN I STÓP
PROCENTOWYCH W POLSCE I USA
– PRZYKŁAD OSZACOWA MODELU MULTIPLIKATYWNEGO
Rozwa my przykład dotycz cy zale no ci pomi dzy nominalnym kursem dolara
ameryka skiego na rynku polskim a poziomem cen i stóp procentowych w Polsce i w Stanach
Zjednoczonych Ameryki Północnej w okresie od I kwartału 1997 roku do II kwartału 2002
roku. Analizowane okresy oznaczono subskryptem t, gdzie t=1,2,...,22. Punktem wyj cia przy
konstrukcji modelu jest zało enie w my l którego nominalny kurs dolara USA (
y
t
), wyra ony
redni cen kwartaln [zł/ 1 USD], jest:
•
dodatnio uzale niony od kursu dolara na rynku wiatowym (za granic ) (
ef
t
)
•
dodatnio uzale niony od redniego kwartalnego poziomu cen w Polsce ( w kraju) (
pd
t
),

15
•
ujemnie uzale niony od redniego kwartalnego poziomu cen w USA (za granic ) (
pf
t
),
•
ujemnie uzale niony od stopy procentowej w Polsce (w kraju) (
id
t
),
•
dodatnio uzale niony od stopy procentowej w USA (za granic ) (
if
t
).
Informacje kwartalne dotycz ce wyró nionych zmiennych zamieszczono w Tabeli 1.
TABELA 1
Kurs dolara na rynku krajowym i zagranicznym
oraz poziomy cen i stopy dyskontowe w Polsce i USA
w okresie od I kwartału 1997 roku do II kwartału 2002 roku
Numer
okresu (t) oraz
rok
i kwartał
(Q)
Kurs dolara
USA
Zł/1USD
Kurs dolara
USA
na rynku
wiatowym
(
EURO-DM)/
/1USD
Poziom cen
w Polsce
1993Q1=1,0
Poziom cen
w USA
1993Q1=1,00
Stopa
redyskonto-
wa w
Polsce
(stan na
pocz tek
okresu)
Stopa
dyskontowa
w USA
(stan na
pocz tek
okresu)
t
Rok i
kwartał
y
t
ef
t
pd
t
pf
t
id
t
if
t
1
2
3
4
5
6
7
8
1
1997Q1
3,0115
0,8527
2,4596
1,1162
0,220
0,050
2
1997Q2
3,1770
0,8813
2,5347
1,1183
0,220
0,050
3
1997Q3
3,4449
0,9188
2,5644
1,1238
0,220
0,050
4
1997Q4
3,4837
0,8997
2,6504
1,1300
0,245
0,050
5
1998Q1
3,5098
0,9347
2,8015
1,1330
0,245
0,050
6
1998Q2
3,4390
0,9180
2,8667
1,1360
0,245
0,050
7
1998Q3
3,5503
0,8909
2,8516
1,1415
0,235
0,050
8
1998Q4
3,4770
0,8557
2,8942
1,1470
0,215
0,050
9
1999Q1
3,7587
0,9067
2,9752
1,1518
0,182
0,045
10
1999Q2
3,9605
0,9567
3,0502
1,1595
0,155
0,045
11
1999Q3
3,9712
0,9433
3,0570
1,1681
0,155
0,045
12
1999Q4
4,1772
0,9833
3,1605
1,1773
0,155
0,048
13
2000Q1
4,1119
1,0333
3,2816
1,1896
0,190
0,050
14
2000Q2
4,3776
1,0767
3,3552
1,1979
0,200
0,055
15
2000Q3
4,3907
1,1133
3,3872
1,2088
0,200
0,060
16
2000Q4
4,5034
1,1400
3,4513
1,2174
0,215
0,060
17
2001Q1
4,0876
1,0967
3,5015
1,2323
0,215
0,060
18
2001Q2
3,9895
1,1633
3,5766
1,2374
0,195
0,045
19
2001Q3
4,2168
1,1100
3,5532
1,2423
0,180
0,033
20
2001Q4
4,0806
1,1200
3,5790
1,2417
0,170
0,025
21
2002Q1
4,1297
1,1567
3,6206
1,2476
0,140
0,0125
22
2002Q2
4,0430
1,0600
3,6517
1,2587
0,120
0,0125
ródło: Opracowanie własne na podstawie danych statystycznych GUS
Warto zaznaczy , e kurs dolara na rynkach wiatowych mierzono w markach niemieckich
przeliczonych na EURO. Model w wersji multiplikatywnej przyjmie posta :
t
t
if
5
b
t
id
4
b
3
b
t
2
b
t
1
b
t
0
t
v
e
pf
pd
ef
B
y
⋅⋅⋅⋅
====
++++
(77)
W wersji zlinearyzowanej model ten zapiszemy nast puj co:
t
t
5
t
4
t
3
t
2
t
1
0
t
u
if
b
id
b
pf
ln
b
pd
ln
b
ef
ln
b
b
y
ln
++++
++++
++++
++++
++++
++++
====
,
(78)
gdzie:
0
0
B
ln
b ====
,
t
t
v
ln
u ====

16
Zauwa my, ze parametry strukturalne
b
i
s elastyczno ciami lub quasi elastyczno ciami kursu
dolara wzgl dem odpowiednich czynników, jako e:
0
b
ef
/
ef
y
/
y
ef
ln
y
ln
E
1
t
t
t
t
t
t
)
w
(
y
>>>>
====
∆∆∆∆
∆∆∆∆
≅≅≅≅
∆∆∆∆
∆∆∆∆
====
εεεε
,
(79.1)
0
b
pd
/
pd
y
/
y
pd
ln
y
ln
E
2
t
t
t
t
t
t
)
pd
(
y
>>>>
====
∆∆∆∆
∆∆∆∆
≅≅≅≅
∆∆∆∆
∆∆∆∆
====
,
(79.2)
0
b
pf
/
pf
y
/
y
pf
ln
y
ln
E
3
t
t
t
t
t
t
)
pf
(
y
<<<<
====
∆∆∆∆
∆∆∆∆
≅≅≅≅
∆∆∆∆
∆∆∆∆
====
,
(79.3)
0
b
id
y
/
y
id
y
ln
E
4
t
t
t
t
t
)
if
(
y
>>>>
====
∆∆∆∆
∆∆∆∆
≅≅≅≅
∆∆∆∆
∆∆∆∆
====
,
(79.4)
0
b
if
y
/
y
if
y
ln
E
5
t
t
t
t
t
)
if
(
y
>>>>
====
∆∆∆∆
∆∆∆∆
≅≅≅≅
∆∆∆∆
∆∆∆∆
====
,
(79.5)
Znaki parametrów b d cymi elastyczno ciami cenowymi wynikaj z przyj tych zało e
dotycz cych charakteru zwi zku pomi dzy zmiennymi. Poniewa stopy procentowe uj to w
postaci ułamkowej, wi c wyra enia (79.4) i (79.5) uzna mo na za quasi elastyczno ci. Na
ich podstawie powiemy o ile procent zmieni si kurs dolara, je li odpowiednia stopa
procentowa wzro nie o jeden punkt procentowy.
Na podstawie danych statystycznych zamieszczonych w Tabeli 1, stosuj MNK,
oszacowano zlinearyzowan wersj modelu multiplikatywnego. Oszacowana posta
strukturalna w wersji transformowanej przedstawia nast puj co:
t
)
837
,
2
(
t
)
205
,
3
(
t
)
262
,
2
(
t
)
693
,
3
(
t
)
347
,
2
(
)
73
,
2
(
t
if
639
,
2
id
115
,
1
pf
ln
47
,
2
pd
ln
055
,
1
ef
ln
527
,
0
6596
,
0
yˆ
ln
++++
−−−−
−−−−
++++
++++
====
−−−−
−−−−
.
(80)
R
2
= 0,9261,
034184
,
0
ˆ
u
====
σσσσ
,
DW= 1,9736
Pod ocenami parametrów strukturalnych umieszczono warto ci statystyk
t-Studenta. Z ich
analiz wynika, e parametry strukturalne uzna nale y za statystycznie istotnie ró ni ce si od
zera. Oznacza to, e zmienne wyst puj ce przy odpowiednich parametrach uzna nale y za
statystycznie istotnie oddziaływuj ce na zmienn obja nian . O poprawno ci takiego
wnioskowania wiadczy mi dzy innymi warto statystyki
DW wskazuj ca na brak
autokorelacji składników losowych. O ogólnym stopniu dopasowania modelu do danych
obserwowanych wnioskowa mo emy na podstawie współczynnika determinacji (
R
2
) oraz
miar wzgl dnego rozproszenia zmiennej obja nianej w relacji do warto ci teoretycznych
oszacowanych na poziomie warunkowych rednich geometrycznych. rednie te wyznaczamy
na podstawie antylogarytmowanej postaci modelu (80). Posta t zapiszemy nast puj co:
t
if
639
,
2
t
id
115
,
1
47
,
2
t
055
,
1
t
527
,
0
t
t
e
pus
pd
ef
934
,
1
yˆ
++++
−−−−
−−−−
⋅⋅⋅⋅
⋅⋅⋅⋅
⋅⋅⋅⋅
====
.
(81)
W kolumnach (5) i (7) Tabeli 2 zamieszczono warto ci teoretyczne obliczono odpowiednio na
podstawie (80) i (81). Zgodnie z (61) i (62), co uwidoczniono w kolumnach 6 i 8
analizowanej tabeli, w ka dym z przypadków, gdy zmienna obja niana jest mniejsza od jej
warto ci teoretycznej wówczas jej udział w warto ci teoretycznej jest mniejszy od jeden a tym
samym ró nica logarytmów zmiennej i jej warto ci teoretycznej jest ujemna. Ponadto
stwierdzamy, e zawsze wtedy gdy zmienna obja niana jest wi ksza od jej warto ci
teoretycznej, to jej udział w warto ci teoretycznej ma warto wi ksz od jeden a tym samym
ró nica logarytmów zmiennej i jej warto ci teoretycznej jest dodatnia. W uj ciu procentowym

17
wzgl dne odchylenia warto ci obserwowanych od warto ci teoretycznych przedstawiono w
kolumnie 9 Tabeli 2.
TABELA 2
Warto ci rzeczywiste i teoretyczne kursu dolara ameryka skiego na rynku polskim
w okresie od I kwartału 1997 roku do II kwartału 2002 roku
Numer
okresu (t) oraz
rok
i kwartał (Q)
Kurs
dolara
USA
Zł/1USD
Logarytm
naturalny
warto ci
obserwo-
wanych
kursu
dolara
Logarytm
naturalny
warto ci
teoretycz-
nych
kursu
dolara
Reszty
postaci
zlogaryt-
mowanej
modelu
Warto ci
teoretyczne
postaci
zdelogaryt-
mowanej
modelu
Udział
warto ci
obserwo-
wanych
w warto -
ciach
teoretycz-
nych
Odchylenie
warto ci
rzeczywistych
od warto ci
teoretycznych
w procentach
t
Rok i
kwartał
y
t
ln y
t
t
yˆ
ln
û
t
=
lny
t
-ln
t
t
yˆ
t
t
t
yˆ
/
y
vˆ ====
%
100
)
yˆ
/
ˆ
(
t
εεεε
1
2
3
4
5
6
7
8
9
1 1997Q1
3,0115
1,1024
1,1404 -0,037929
3,1279
0,96278
-3,72%
2 1997Q2
3,1770
1,1559
1,1849 -0,028986
3,2704
0,97143
-2,86%
3 1997Q3
3,4449
1,2369
1,2070 0,029895
3,3434
1,03030
3,03%
4 1997Q4
3,4837
1,2481
1,1892 0,058901
3,2844
1,06070
6,07%
5 1998Q1
3,5098
1,2556
1,2614 -0,005791
3,5302
0,99942
-0,06%
6 1998Q2
3,4390
1,2352
1,2696 -0,034449
3,5595
0,96614
-3,39%
7 1998Q3
3,5503
1,2670
1,2474 0,019606
3,4814
1,01980
1,98%
8 1998Q4
3,4770
1,2462
1,2522 -0,006074
3,4982
0,99394
-0,66%
9 1999Q1
3,7587
1,3241
1,3251 -0,001035
3,7626
0,99897
-0,10%
10 1999Q2
3,9605
1,3764
1,3934 -0,017062
4,0287
0,98308
-1,69%
11 1999Q3
3,9712
1,3791
1,3702 0,008870
3,9361
1,00890
0,89%
12 1999Q4
4,1772
1,4296
1,4156 0,014024
4,1190
1,01410
1,41%
13 2000Q1
4,1119
1,4139
1,4221 -0,008193
4,1457
0,99184
-0,82%
14 2000Q2
4,3776
1,4765
1,4520 0,024544
4,2715
1,02480
2,48%
15 2000Q3
4,3907
1,4795
1,4704 0,009126
4,3508
1,00920
0,92%
16 2000Q4
4,5034
1,5048
1,4685 0,036349
4,3426
1,03700
3,70%
17 2001Q1
4,0876
1,4080
1,4332 -0,025243
4,1921
0,97507
-2,49%
18 2001Q2
3,9895
1,3837
1,4592 -0,075506
4,3024
0,92727
-7,27%
19 2001Q3
4,2168
1,4391
1,4029 0,036225
4,0668
1,03690
3,69%
20 2001Q4
4,0806
1,4062
1,4064 -0,000204
4,0814
0,99980
-0,02%
21 2002Q1
4,1297
1,4182
1,4244 -0,006188
4,1553
0,99383
-0,62%
22 2002Q2
4,0430
1,3970
1,3879 0,009102
4,0063
1,00920
0,92%
ródło: Obliczenia własne na podstawie danych statystycznych z Tabeli 1.
Obecnie wykorzystuj c bł d standardowy reszt mo emy oszacowa zdefiniowane w
(71) i (72) miary przeci tnego wzgl dnego rozproszenia warto ci rzeczywistych
(obserwowanych) w relacji do ich warto ci teoretycznych. Miary te wynosz odpowiednio:
9664
,
0
e
e
v
034184
,
0
u
ˆ
d
====
====
====
−−−−
σσσσ
−−−−
,
(82)
03477
,
1
e
e
v
034184
,
0
u
ˆ
g
====
====
====
σσσσ
.
(83)
Na podstawie powy szych miar powiemy, e
w sensie standardowym przeci tny udział
warto ci rzeczywistych (obserwowanych) zmiennej y
t
w warto ciach teoretycznych
modelu multiplikatywnego waha si w granicach od 0,9664 do 1,03477. Z drugiej strony
poniewa
0,9664-1=-0,0336 oraz 1,03477-1=0,03477, wi c stwierdzamy, e w sensie
18
standardowym warto ci zmiennej obja nianej odchylaj si od warto ci teoretycznych
rednio w przedziale od –3,36% do 3,48%.
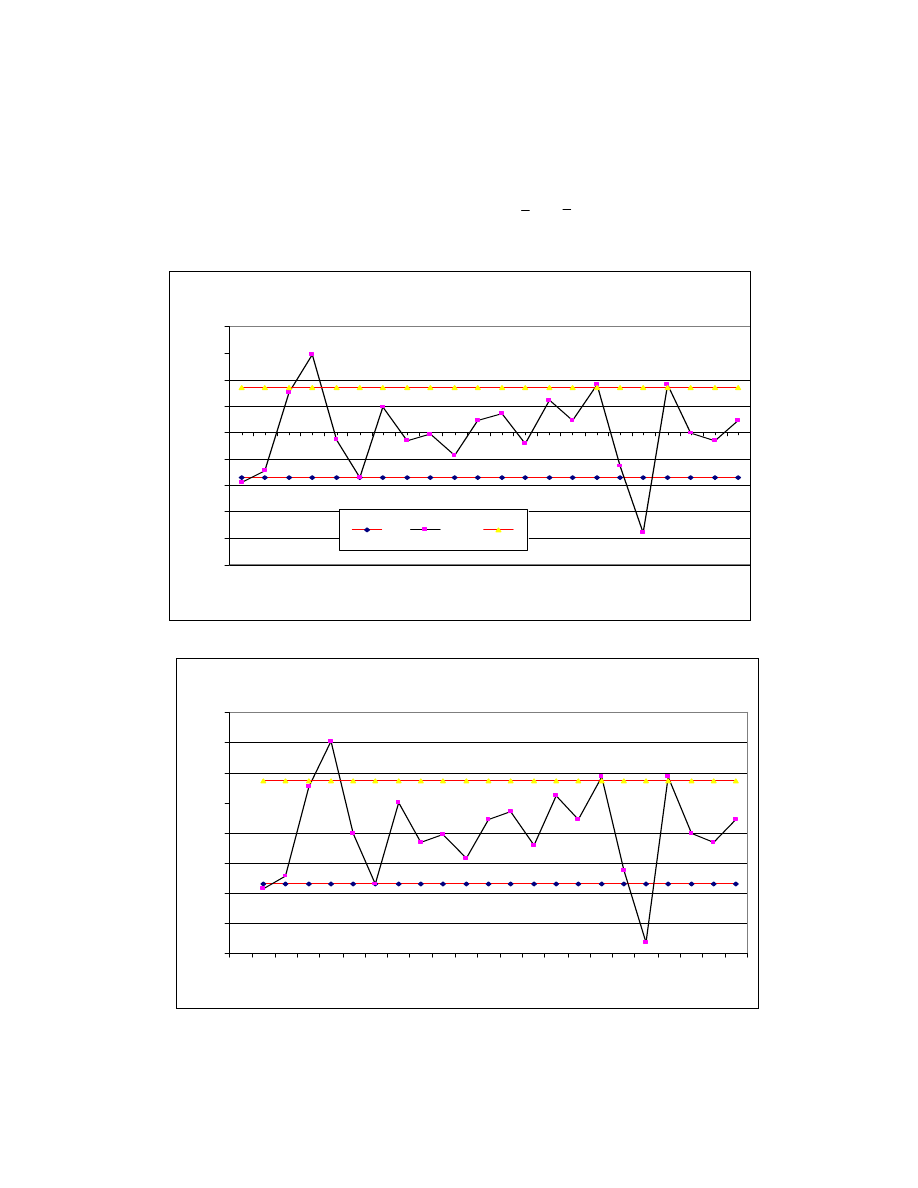
Dla lepszego zobrazowania opisanej powy ej sytuacji na wykresie 1 przedstawiono
reszty
t
t
t
yˆ
ln
y
ln
uˆ
−−−−
====
w otoczeniu ich odchylenia standardowego
u
ˆσσσσ
±±±±
. Z kolei wykres 2
obrazuje udział warto ci rzeczywistych
y
t
w warto ciach teoretycznych, tzn.
t
t
t
yˆ
/
y
vˆ ====
w
otoczeniu oszacowanych zgodnie z (82) i (83) miar
d
v
i
g
v
wskazuj cych na przeci tny
udział warto ci rzeczywistych w warto ciach teoretycznych.
Wykres 1 Reszty postaci zlogarytmowanej modelu multiplikatywnego
wraz z odchyleniem standardowym
-0,1
-0,08
-0,06
-0,04
-0,02
0
0,02
0,04
0,06
0,08
19
97
Q1
19
97
Q3
19
98
Q1
19
98
Q3
19
99
Q1
19
99
Q3
20
00
Q1
20
00
Q3
20
01
Q1
20
01
Q3
20
02
Q1
ût
Wykres 2 Udział warto ci rzeczywistych y w ich warto ciach
teoretycznych wraz z miarami wzgl dnego rozproszenia
0,92
0,94
0,96
0,98
1
1,02
1,04
1,06
1,08
Ok
re
s
19
97
Q2
19
97
Q4
19
98
Q2
19
98
Q4
19
99
Q2
19
99
Q4
20
00
Q2
20
00
Q4
20
01
Q2
20
01
Q4
20
02
Q2

19
Na podstawie oszacowanych parametrów strukturalnych modelu powiemy, e w
warunkach stało ci pozostałych zmiennych:
•
wzrost kursu dolara na rynku wiatowym wzgl dem DM/EURO o 1% prowadzi do
wzrostu kursu dolara na rynku polskim przeci tnie o 0,527 %,
•
wzrost poziomu cen w Polsce o 1% prowadzi do wzrostu kursu dolara na rynku
krajowym przeci tnie o 1,055 %,
•
wzrost poziomu cen w USA o 1% prowadzi do spadku kursu dolara na rynku
krajowym przeci tnie o 2,47 %,
•
wzrost stóp procentowych w Polsce o 1 punkt procentowy prowadzi do spadku
kursu dolara na rynku krajowym przeci tnie o 1,115 % (quasi elastyczno ),
•
wzrost stóp procentowych w USA o 1 punkt procentowy prowadzi do wzrostu
kursu dolara na rynku krajowym przeci tnie o 2,64 % (quasi elastyczno ).
9. UPROSZCZONA MIARA PRZECI TNEGO UDZIAŁU RESZT
W WARTO CIACH TEORETYCZNYCH POSTACI PIERWOTNEJ
MODELU MULTIPLIKATYWNEGO
Omawiane powy ej miary wzgl dnego rozproszenia wyznaczaj dobr podstaw do
wnioskowania o wła ciwo ciach estymacji przedziałowej modeli multiplikatywnych. Jak
wynika z przeprowadzonych powy ej rozwa a dokładna jedno punktowa ocena rozproszenia
warto ci empirycznych wzgl dem warto ci teoretycznych jest mo liwa jedynie dla postaci
zlinearyzowanej rozpatrywanej klasy modeli. Dla postaci pierwotnej modelu
multiplikatywnego, ewentualna punktowa ocena rozproszenia nie mo e mie charakteru
jednorodnego w sensie metodologicznym. Aby si o tym przekona rozwa my informacje o
procentowym udziale reszt w warto ciach teoretycznych pierwotnej postaci modelu
multiplikatywnego. Wyniki oblicze przedstawiono w kolumnie 9 Tabeli 2. Wyznaczono je
na podstawie przekształconego w nast puj cy sposób wyra enia (60):
)
1
vˆ
(
yˆ
yˆ
y
yˆ
ˆ
t
t
t
t
t
t
−−−−
====
−−−−
====
εεεε
(84)
Z analizy dokonanych oblicze wynika, e stosunkowo najwi ksze ró nice wzgl dne
pomi dzy warto ciami rzeczywistymi i teoretycznymi wyst piły w 4 kwartale 1997 roku
(6,07%) oraz 2 kwartale 2001 roku (-7,27%). Przy czym odchylenie absolutne w pierwszym
wypadku wynosiło (3,4837-3,2844) = 0,1993 zł/1USD, natomiast w drugim przypadku
(3,9895-4,3024) = -0,3129 zł/1 USD. Na podstawie analizowanych informacji zaproponowa
mo emy
miernik charakteryzuj cy redni kwadratowy udział reszt w warto ciach
teoretycznych modelu, zgodnie z nast puj c zasad :
)
1
k
(
n
yˆ
ˆ
ˆ
n
1
t
2
t
t
2
yˆ
/
ˆ
++++
−−−−
εεεε
====
σσσσ
====
εεεε
(85)
Powy szy miernik nie jest jednorodny metodologicznie, gdy przy jej definiowaniu
wykorzystujemy dwa rodzaje rednich, tzn. redni arytmetyczn i redni geometryczn .
Zauwa my bowiem, e reszty definiowane s jako ró nice pomi dzy warto ciami
rzeczywistymi i warto ciami teoretycznymi oszacowanymi na poziomie rednich
geometrycznych. Z kolei wariancja udziału reszt w warto ciach teoretycznych ma charakter
redniej arytmetycznej. Obecnie
przeci tny udział reszt w warto ciach teoretycznych
zdefiniujemy jako dodatni pierwiastek kwadratowy wariancji okre lonej w (85), tzn.:
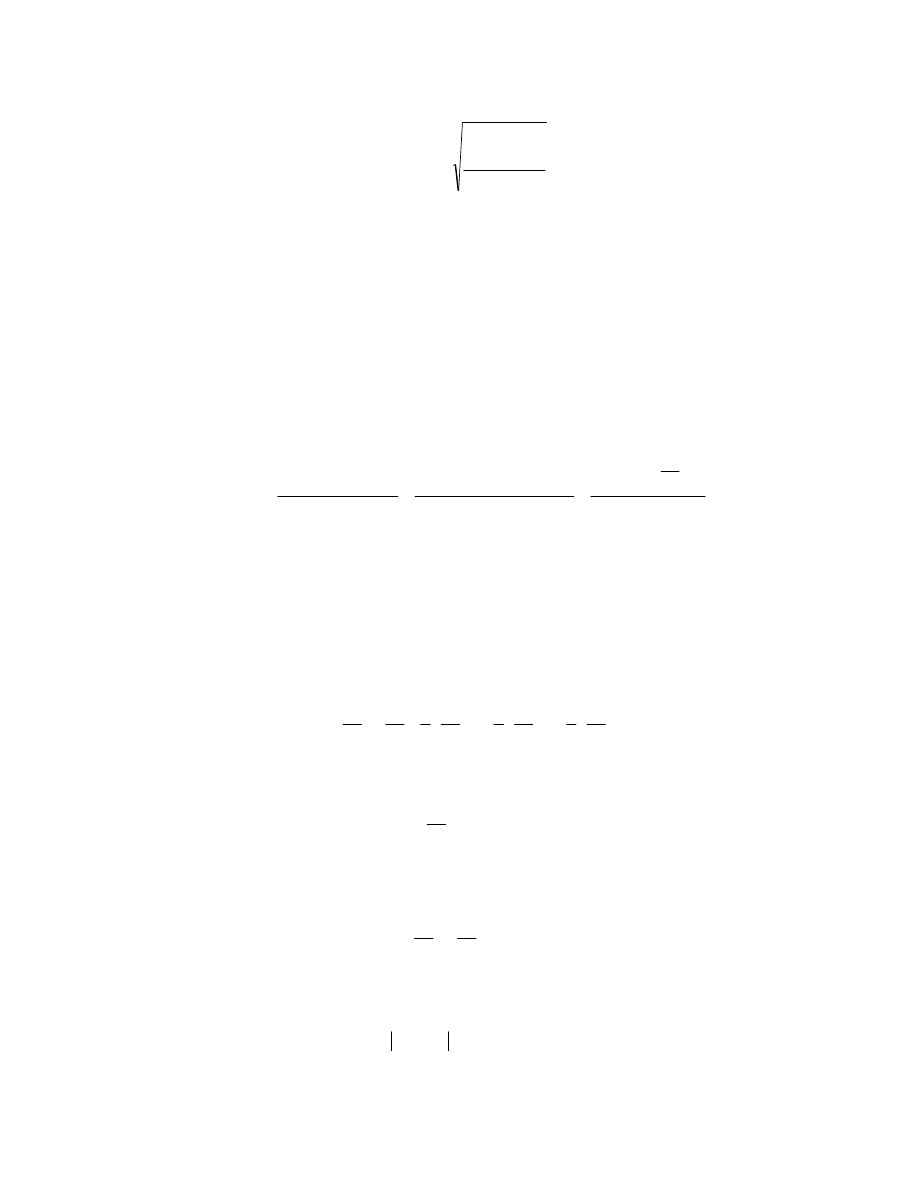
20
((((
))))
2
n
1
t
2
t
t
yˆ
/
ˆ
)
1
k
(
n
yˆ
/
ˆ
ˆ
++++
−−−−
εεεε
====
σσσσ
====
εεεε
(86)
Na podstawie informacji zawartych w Tabeli 2 stwierdzamy, e
2
yˆ
/
ˆ
ˆ
εεεε
σσσσ
=0,0011709. Oznacza
to, e
yˆ
/
ˆ
ˆ
εεεε
σσσσ
=0,0342. Powiemy wi c, e przeci tny udział reszt w warto ciach
teoretycznych modelu (oszacowanych na poziomie warunkowych rednich geometrycznych)
wynosi 3,42%.
Powy szy sposób oszacowania wzgl dnego rozproszenia warto ci rzeczywistych
wzgl dem warto ci teoretycznych wymaga zastosowania niestandardowych procedur
obliczeniowych. W tej sytuacji zastanówmy si nad mo liwo ci zdefiniowania
uproszczonego miernika charakteryzuj cego wzgl dne rozproszenie, przy definiowaniu
którego mogliby my wykorzysta standardowe oszacowania zlinearyzowanych postaci
modeli multiplikatywnych. W tym celu zdefiniowan w (68) wariancj resztow
przekształ my do nast puj cej postaci:
)
1
k
(
n
yˆ
ˆ
1
ln
)
1
k
(
n
]
yˆ
ln
)
ˆ
yˆ
[ln(
)
1
k
(
n
)
yˆ
ln
y
(ln
ˆ
n
1
t
2
t
t
n
1
t
2
t
t
t
n
1
t
2
t
t
2
u
++++
−−−−
εεεε
++++
====
++++
−−−−
−−−−
εεεε
++++
====
++++
−−−−
−−−−
====
σσσσ
====
====
====
(87)
Przy przekształceniach dokonanych w powy szym wzorze wykorzystano zdefiniowan w
(60) ocen absolutnego zakłócenia
t
ˆεεεε
. Ocena ta wskazuje na ró nic pomi dzy warto ci
rzeczywist zmiennej obja nianej modelu a warto ci teoretyczn tej zmiennej wyznaczon
na poziomie warunkowej redniej geometrycznej. Tym samym, zgodnie z (84), relacja
t
t
yˆ
/
ˆεεεε
okre la ocen udziału reszt postaci pierwotnej modelu w warto ciach teoretycznych, które s
oszacowane na poziomie warunkowej redniej geometrycznej w okresie
t. Zauwa my, e
wyra enie zawarte w nawiasie kwadratowym mo emy rozpisa w szereg pot gowy o
nast puj cej postaci:
⋅⋅⋅⋅⋅
⋅⋅⋅
⋅⋅⋅⋅
±±±±
εεεε
−−−−
εεεε
++++
εεεε
−−−−
εεεε
====
εεεε
++++
4
t
t
3
t
t
2
t
t
t
t
t
t
yˆ
ˆ
4
1
yˆ
ˆ
3
1
yˆ
ˆ
2
1
yˆ
ˆ
yˆ
ˆ
1
ln
(88)
Powy szy szereg jest zbie ny dla nast puj cego obszaru zmienno ci elementów
wyst puj cych w (88):
1
yˆ
ˆ
1
t
t
≤≤≤≤
εεεε
<<<<
−−−−
(89)
Dla realnie spotykanych w modelach multiplikatywnych udziału reszt w warto ciach
teoretycznych uprawnione jest nast puj ce przybli enie:
t
t
t
t
yˆ
ˆ
yˆ
ˆ
1
ln
εεεε
≅≅≅≅
εεεε
++++
(90)
Przed sformułowaniem ostatecznych wniosków zauwa my, e dla pewnej dodatniej liczby a,
gdy 0<a<1, spełnione s nast puj ce nierówno ci:
a
)
a
1
ln(
>>>>
−−−−
(91.1)

21
a
)
a
1
ln(
<<<<
++++
(92.2)
W wietle powy szego powiemy, e:
•
w przypadku ujemnych reszt postaci zlogarytmowanej modelu multiplikatywnego,
przeszacowujemy odchylenia wzgl dne,
•
w przypadku dodatnich reszt postaci zlogarytmowanej modelu multiplikatywnego,
niedoszacowujemy odchylenia wzgl dne.
Na przykład niech udział reszty
t
ˆεεεε
w warto ci teoretycznej modelu
t
yˆ
wyniesie
-15% (tzn.
w postaci ułamkowej
15
,
0
]
yˆ
/
ˆ
[
−−−−
====
εεεε
), wówczas otrzymujemy:
1625
,
0
85
,
0
ln
)
15
,
0
1
ln(
)
yˆ
/
ˆ
1
ln(
yˆ
ln
y
ln
uˆ
ln
−−−−
====
====
−−−−
====
εεεε
−−−−
====
−−−−
====
.
Stwierdzamy tym samym, e spełniona jest nierówno (91.1). Je li obecnie uznamy, e
udział reszty w warto ci teoretycznej modelu wyniesie
15% (tzn. w postaci ułamkowej
15
,
0
]
yˆ
/
ˆ
[
====
εεεε
), wówczas otrzymujemy:
13976
,
0
15
,
1
ln
)
15
,
0
1
ln(
)
yˆ
/
ˆ
1
ln(
yˆ
ln
y
ln
uˆ
ln
====
====
++++
====
εεεε
−−−−
====
−−−−
====
.
Tym samym spełniona jest nierówno (91.2). Z punktu widzenia kryterium estymacji modeli
multiplikatywnych i wła ciwo ci reszt postaci zlinearyzowanej modelu wa na jest
nast puj ca prawidłowo wynikaj ca z powy ej wykazanych wła ciwo ci:
[[[[
]]]] [[[[
]]]]
2
2
2
1
2
2
2
1
)
a
(
)
a
(
)
a
1
ln(
)
a
1
ln(
<<<<
−−−−
++++
====
−−−−
,
(92)
gdzie:
0<a
1
,a
2
<1.
W rezultacie uwzgl dniaj c (90) oraz (92), wariancj resztow zdefiniowan w (87)
przedstawi mo emy w nast puj cej przybli onej formie:
)
1
k
(
n
yˆ
ˆ
)
1
k
(
n
)
yˆ
ln
y
(ln
ˆ
n
1
t
2
t
t
n
1
t
2
t
t
2
u
++++
−−−−
εεεε
≅≅≅≅
++++
−−−−
−−−−
====
σσσσ
====
====
(90)
Powy sze przybli enie jest stosunkowo dokładne z uwagi na fakt, i w wyniku sumowania
kwadratu reszt postaci zlogarytmowanej modelu multiplikatywnego, niedoszacowania ocen
wzgl dnego rozproszenia dla ujemnych reszt kompensowane s przeszacowaniami ocen
wzgl dnego rozproszenia dla dodatnich reszt. Na podstawie (90) bł d standardowy reszt
zdefiniujemy nast puj co:
((((
))))
2
n
1
t
2
t
t
2
1
t
2
t
t
u
)
1
k
(
n
yˆ
/
ˆ
)
1
k
(
n
)
yˆ
ln
y
(ln
ˆ
++++
−−−−
εεεε
≅≅≅≅
++++
−−−−
−−−−
====
σσσσ
====
====
(91)
Przed sformułowaniem ostatecznych wniosków zatrzymajmy si na chwil przy dokładnych
miarach wzgl dnego rozproszenia zdefiniowanych w (71) i (72). Rozpisuj c je w szeregi
pot gowe otrzymujemy odpowiednio nast puj ce wyra enia:
...
ˆ
6
1
ˆ
2
1
ˆ
1
...
)
ˆ
(
!
3
1
)
ˆ
(
!
2
1
)
ˆ
(
!
1
1
1
e
v
3
u
2
u
u
u
2
u
u
u
ˆ
d
++++
σσσσ
−−−−
σσσσ
++++
σσσσ
−−−−
====
++++
σσσσ
−−−−
++++
σσσσ
−−−−
++++
σσσσ
−−−−
++++
====
====
σσσσ
−−−−
(92.1)
...
ˆ
6
1
ˆ
2
1
ˆ
1
...
)
ˆ
(
!
3
1
)
ˆ
(
!
2
1
)
ˆ
(
!
1
1
1
e
v
3
u
2
u
u
u
2
u
u
u
ˆ
g
++++
σσσσ
++++
σσσσ
++++
σσσσ
++++
====
++++
σσσσ
++++
σσσσ
++++
σσσσ
++++
====
====
σσσσ
(92.2)
Po prostym przekształceniu powy szych wyra e otrzymujemy:

22
...
24
1
ˆ
6
1
ˆ
2
1
ˆ
1
v
4
u
3
u
2
u
u
d
−−−−
σσσσ
++++
σσσσ
−−−−
σσσσ
++++
σσσσ
−−−−
====
−−−−
(93.1)
...
24
1
ˆ
6
1
ˆ
2
1
ˆ
1
v
4
u
3
u
2
u
u
g
++++
σσσσ
++++
σσσσ
++++
σσσσ
++++
σσσσ
====
−−−−
(93.2)
Odejmuj c stronami od równania (93.2) równanie (93.1) stwierdzamy, e:
u
5
u
3
u
u
d
g
ˆ
2
...
60
1
ˆ
3
1
ˆ
2
v
v
σσσσ
≅≅≅≅
++++
σσσσ
++++
σσσσ
++++
σσσσ
====
−−−−
(94)
Z powy szego wynika, e:
2
v
v
ˆ
d
g
u
−−−−
≅≅≅≅
σσσσ
(95)
Obecnie na podstawie (91) oraz (95) powiemy, e
bł d standardowy reszt postaci
zlogarytmowanej modelu multiplikatywnego z pewnym przybli eniem wyznacza redni
udział reszt postaci pierwotnej modelu w warto ciach teoretycznych oszacowanych na
poziomie redniej geometrycznej w danej próbie statystycznej. Wnioskowanie to uzna
nale y za poprawne w przypadku, gdy podstaw logarytmowania jest liczba naturalna „
e”. W
analizowanym przez nas przypadku
σσσσ
u
=0,034181. Zgodnie wi c z (91) powiemy, e z
pewnym przybli eniem
przeci tny udział reszt postaci zdelogarytmowanej modelu w jego
warto ciach teoretycznych wynosi około 3,419%. Z drugiej strony, gdyby zastosowa wzór
(95) otrzymaliby my nast puj cy wynik: [(1,03477-0,9664)/2]100% =
3,4185%. Potwierdza
to, wcze niej sformułowane na gruncie teoretycznym, wnioski o mo liwo ciach stosowania w
praktyce przybli onych miar okre laj cych wzgl dne rozproszenie warto ci rzeczywistych
zmiennej obja nianej w relacji do jej warto ci teoretycznych.
LITERATURA
[1] Aitchison J., Brown A., The Lognormal Distribution, Cambridge University Press, Cambidge 1957.
[2] Bołt T.W., Ossowski J., Prognozowanie na podstawie modeli logarytmiczno-liniowych, Przegl d
Statystyczny 1992, z. 3-4 s.327-340.
[3] Bradu D., Mundlak Y., Estimation in Lognormal Linear Models, Journal of the American Staistical
Association, 1970 nr 65, s.198-211.
[4] Bronsztejn J.N., Siemiendiajew K.A., Matematyka. Poradnik encyklopedyczny, PWN, Warszawa 1976
[5] Goldberger A.S., Teoria ekonometrii, PWE, Warszawa 1972.
[6] Golberger A.S., The Interpretation and Estimation of Cobb-Douglas Functions, Econometrica, 1968 nr 35,
s. 464-472.
[7] Heien D.M.: Not on Log-linear Regression, Journal on the American Statistical Associacion, 1968 nr 63,
s.1034-1038
[8] Kendall M. Bucland W.R., Słownik terminów statystycznych, PWE, Warszawa 1975.
[9] Klein L.R., Wst p do ekonometrii, PWE, Warszawa 1965.
[10] Kmenta J.: Elements of Econometrics, Second Edition, Macmillan Publishing Company, New York 1990.
[11] Murti V.N., Sastry V.K., Production Functions for Indian Industry, Economerica, 1957 nr 25, s. 205-221.
[12] Ossowski J., Własno ci interpretacyjne składnika losowego w modelu multiplikatywnym, Przegl d
Statystyczny 1988, z.2, s.131-142.
[13] Ossowski J., Modele klasy logarytmiczno-liniowej w analizie efektywno ci procesu produkcji,
Wydawnictwo Uniwersytetu Gda skiego, Gda sk 1989, Zeszyty Naukowe, Rozprawy i Monografie 130.
[14] Pawłowski Z., Wst p do statystyki matematycznej, PWN, Warszawa 1969.
[15] Teekens R., Koerts J.., Some Statistical Implications of the Log Transformations of Multiplicative Models,
Econometrica, 1972 nr 5 , s. 793-819.
[16] Theil H., Zasady ekonometrii, PWN, Warszawa 1979
Wyszukiwarka
Podobne podstrony:
Informatyka, INFORMa, Bloki kombinacyjne średniego stopnia scalenia: multiplekser, demultiplekser(de
Ossowska Rycerz w średniowieczu
Wobec Boga i świata modele postaw w utworach średniowiecznych
MODELE GEOMETRYCZNE
Wobec Boga i świata modele postaw w utworach średniowiecznyc
Wobec Boga i świata - modele postaw w utworach średniowiecznych, P-Ż
Planimetria Geometria Szkoła średnia zadania z matematyki Zadania info, 18 (poziom łatwy podstawow
Maria Ossowska Rycerz w średniowieczu
Planimetria Geometria Szkoła średnia zadania z matematyki Zadania info, 18 (poziom łatwy podstawow
modele sezonowe MAŁŻEŃSTWA średnia ruchoma
Planimetria Geometria Szkoła średnia zadania z matematyki Zadania info, 18 (poziom łatwy podstawow
J Ossowski Prognozowanie Na Podstawie Modeli Multiplikatywnych Względne Błędy Prognoz
Maria Ossowska Rycerz w średniowieczu fragmenty
Maria Ossowska Rycerz w średniowieczu
modele sezonowe MAŁŻEŃSTWA średnia ruchoma
Planimetria Geometria Szkoła średnia zadania z matematyki Zadania info, 18 (poziom łatwy podstawow
więcej podobnych podstron