99
WYKŁAD Nr 7
GRANICA FUNKCJI
CIĄGŁOŚĆ I RÓŻNICZKOWALNOŚĆ FUNKCJI JEDNEJ ZMIENNEJ
GRANICA FUNKCJI
Def.7.1. (otoczenie i sąsiedztwo punktu)
Otoczeniem
o promieniu
0
>
r
punktu
R
∈
0
x
nazywamy zbiór:
(
) (
)
r
x
r
x
r
x
U
+
−
=
0
0
0
,
,
Sąsiedztwem
o promieniu
0
>
r
punktu
R
∈
0
x
nazywamy zbiór:
(
) (
) (
)
r
x
x
x
r
x
r
x
S
+
∪
−
=
0
0
0
0
0
,
,
,
Sąsiedztwem
lewostronnym o promieniu
0
>
r
punktu
R
∈
0
x
nazywamy zbiór:
(
) (
)
0
0
0
,
,
x
r
x
r
x
S
−
=
−
Sąsiedztwem
prawostronnym o promieniu
0
>
r
punktu
R
∈
0
x
nazywamy zbiór:
(
) (
)
r
x
x
r
x
S
+
=
+
0
0
0
,
,
Uwaga:
(
) (
)
R
∈
∞
−
=
∞
−
b
b
S
,
,
;
(
) (
)
R
∈
+∞
=
∞
+
a
a
S
,
,
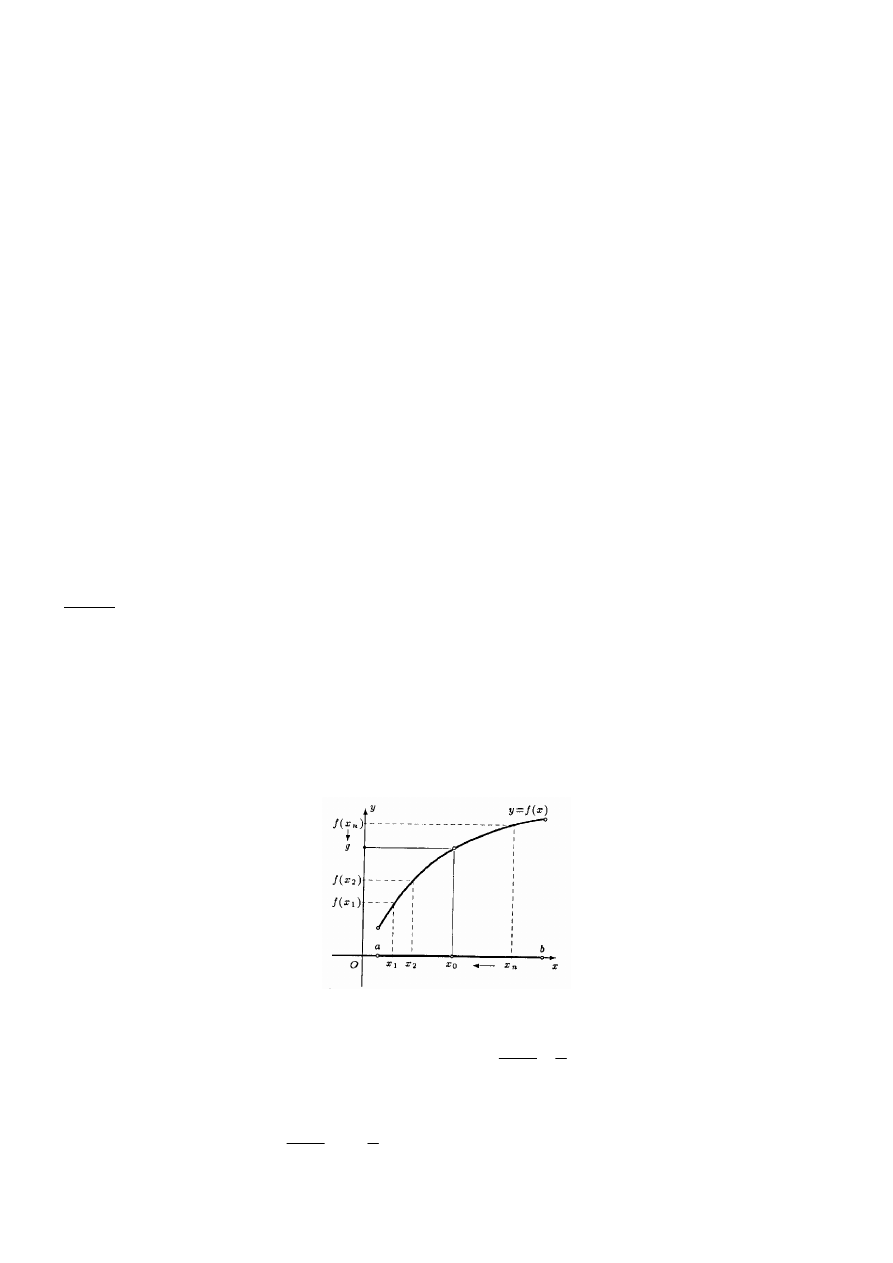
Def.7.2. (granica właściwa funkcji w punkcie wg Heinego)
Niech
R
∈
0
x
oraz niech funkcja f będzie określona przynajmniej na
( )
0
x
S
.
Liczba g jest granicę właściwą funkcji f w punkcie
0
x
( )
( )
( )
=
⇒
=
∈
∀
⇔
=
∞
→
∞
→
→
g
x
f
x
x
x
S
x
x
g
x
f
n
n
n
n
n
n
x
x
lim
lim
,
)
(
lim
0
0
0
Rys.1. Granica właściwa funkcji w punkcie wg Heinego
Przykład: Korzystając z definicji Heinego wykazać, że
2
1
3
lim
2
1
=
+
−
→
x
x
x
.
Rozwiązanie:
W naszym przykładzie
( )
2
1
,
3
2
=
+
=
g
x
x
x
f
.
100
Niech
( )
n
x
dowolny ciąg taki, że
( )
1
−
∈ S
x
n
(tzn.
1
−
≠
∈
∀
n
x
n
N
) oraz
1
lim
−
=
∞
→
n
n
x
.
Tworzymy ciąg wartości funkcji o wyrazie ogólnym:
( )
3
2
+
=
n
n
n
x
x
x
f
, a następnie obliczamy granicę:
( )
( )
2
1
3
1
1
3
lim
lim
3
lim
lim
2
2
2
=
+
−
−
=
+
=
+
=
∞
→
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
x
x
x
x
x
f
.
Ostatecznie
2
1
3
lim
2
1
=
+
−
→
x
x
x
.
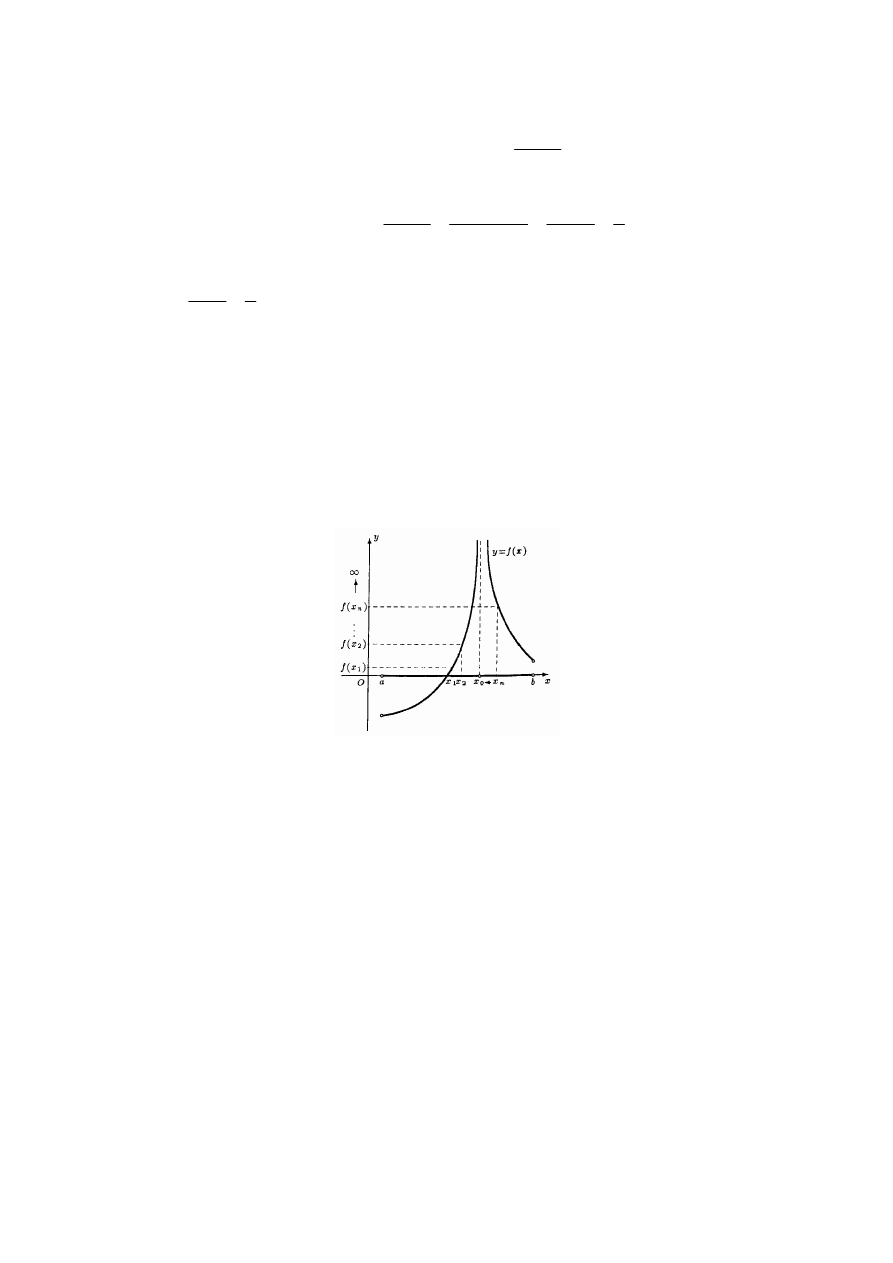
Jeżeli w szczególności ciąg wartości funkcji o wyrazie ogólnym:
( )
n
x
f
ma granicę niewłaściwą
∞
+
lub ∞
−
, mówimy, że funkcja
)
(x
f
ma w punkcie
0
x
granicę niewłaściwą i zapisujemy to
odpowiednio:
( )
( )
( )
+∞
=
⇒
=
∈
∀
⇔
+∞
=
∞
→
∞
→
→
n
n
n
n
n
n
x
x
x
f
x
x
x
S
x
x
x
f
lim
lim
,
)
(
lim
0
0
0
( )
( )
( )
−∞
=
⇒
=
∈
∀
⇔
−∞
=
∞
→
∞
→
→
n
n
n
n
n
n
x
x
x
f
x
x
x
S
x
x
x
f
lim
lim
,
)
(
lim
0
0
0
Rys.2. Granica niewłaściwa funkcji w punkcie wg Heinego
Jeżeli w definicji granicy funkcji
)
(x
f
w punkcie
0
x
(właściwej lub niewłaściwej) zastąpimy
sąsiedztwo
( )
0
x
S
sąsiedztwem prawostronnym
( )
0
x
S
+
, (lewostronnym
( )
0
x
S
−
), to otrzymamy
definicję granicy prawostronnej (lewostronnej) funkcji
)
(x
f
w punkcie
0
x
.
Def.7.3. (granice jednostronne funkcji)
Niech
R
∈
0
x
oraz niech funkcja f będzie określona przynajmniej na
( )
0
x
S
+
.
Wówczas
( )
( )
( )
=
⇒
=
∈
∀
⇔
=
∞
→
∞
→
+
→
+
g
x
f
x
x
x
S
x
x
g
x
f
n
n
n
n
n
n
x
x
lim
lim
,
)
(
lim
0
0
0
Niech
R
∈
0
x
oraz niech funkcja f będzie określona przynajmniej na
( )
0
x
S
−
.
Wówczas
( )
( )
( )
=
⇒
=
∈
∀
⇔
=
∞
→
∞
→
−
→
−
g
x
f
x
x
x
S
x
x
g
x
f
n
n
n
n
n
n
x
x
lim
lim
,
)
(
lim
0
0
0

101
Rys.3. Granica właściwa lewostronna funkcji w punkcie wg Heinego
Przykłady granic niewłaściwych funkcji w punkcie:
a)
+∞
=
=
+
+
−
→
0
4
)
2
(
4
lim
6
2
x
x
b)
{
}
−∞
=
=
+
→
+
0
ln
ln
lim
0
x
x
c)
+∞
=
=
−
→
−
2
tg
tg
lim
2
π
π
x
x
Tw.7.1. (warunek konieczny istnienia granicy funkcji w punkcie)
Funkcja
)
(x
f
ma w punkcie
0
x
granicę (właściwą lub niewłaściwą) ⇔
)
(
lim
)
(
lim
0
0
x
f
x
f
x
x
x
x
−
+
→
→
=
.
Przykład: Zbadać, czy istnieje granica funkcji
x
e
x
f
1
1
1
)
(
+
=
w punkcie
0
0
=
x
.
Rozwiązanie:
Obliczamy granice jednostronne:
0
1
1
1
1
1
1
1
lim
1
0
=
∞
+
=
∞
+
=
+
=
+
∞
+
→
+
e
e
x
x
,
1
1
1
0
1
1
1
1
1
1
lim
1
0
=
=
+
=
+
=
+
∞
−
→
−
e
e
x
x
Ponieważ
)
(
lim
)
(
lim
0
0
x
f
x
f
x
x
x
x
−
+
→
→
≠
, więc nie istnieje
x
x
e
1
0
1
1
lim
+
→
.
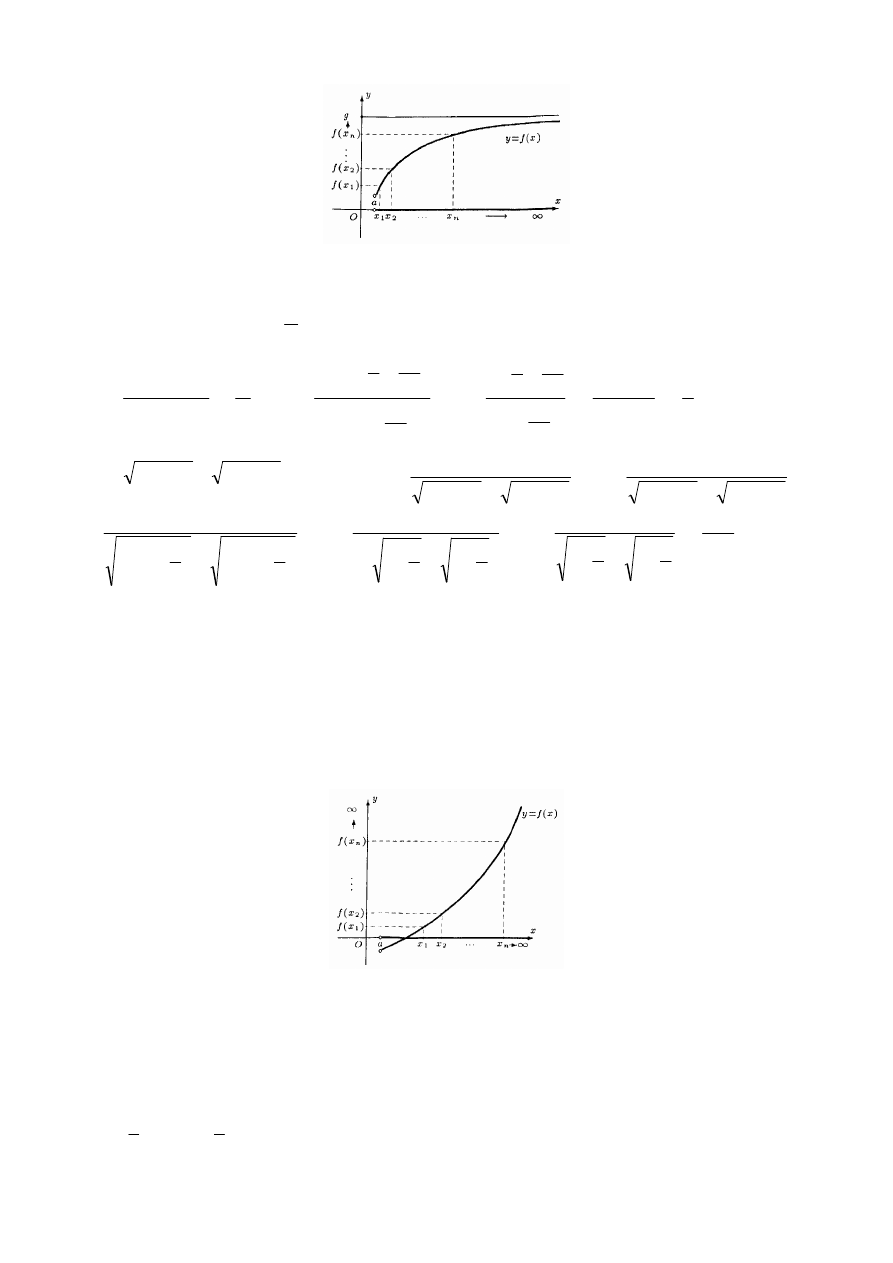
Def.7.4. (granica właściwa funkcji w nieskończoności)
Niech funkcja f będzie określona przynajmniej na
(
)
∞
+
S
.
Wówczas granicę właściwą funkcji f w
∞
+
definiujemy następująco:
( )
(
)
( )
=
⇒
+∞
=
∞
+
∈
∀
⇔
=
∞
→
∞
→
+∞
→
g
x
f
x
S
x
x
g
x
f
n
n
n
n
n
n
x
lim
lim
,
)
(
lim
Analogicznie definiujemy granicę właściwą funkcji f w ∞
−
.
102
Rys.4. Granica właściwa funkcji w nieskończoności wg Heinego
Przykłady granic właściwych funkcji w nieskończoności:
a)
{
}
2
)
arctg(
arctg
lim
π
=
+∞
=
+∞
→
x
x
b)
4
1
0
4
0
0
1
3
4
4
2
1
lim
3
4
4
2
1
lim
3
4
4
2
lim
2
2
2
2
2
2
2
2
=
+
+
+
=
+
+
+
=
+
+
+
=
∞
∞
=
+
+
+
−∞
→
−∞
→
−∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
c)
(
)
[
]
=
−
+
+
=
−
+
+
+
−
+
=
∞
−
∞
=
−
−
+
+∞
→
+∞
→
+∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
4
2
6
lim
4
2
4
2
lim
4
2
lim
2
2
2
2
2
2
2
2
3
1
1
6
4
1
2
1
6
lim
4
1
2
1
6
lim
4
1
2
1
6
lim
2
2
=
+
=
−
+
+
=
−
+
+
=
−
+
+
+∞
→
+∞
→
+∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
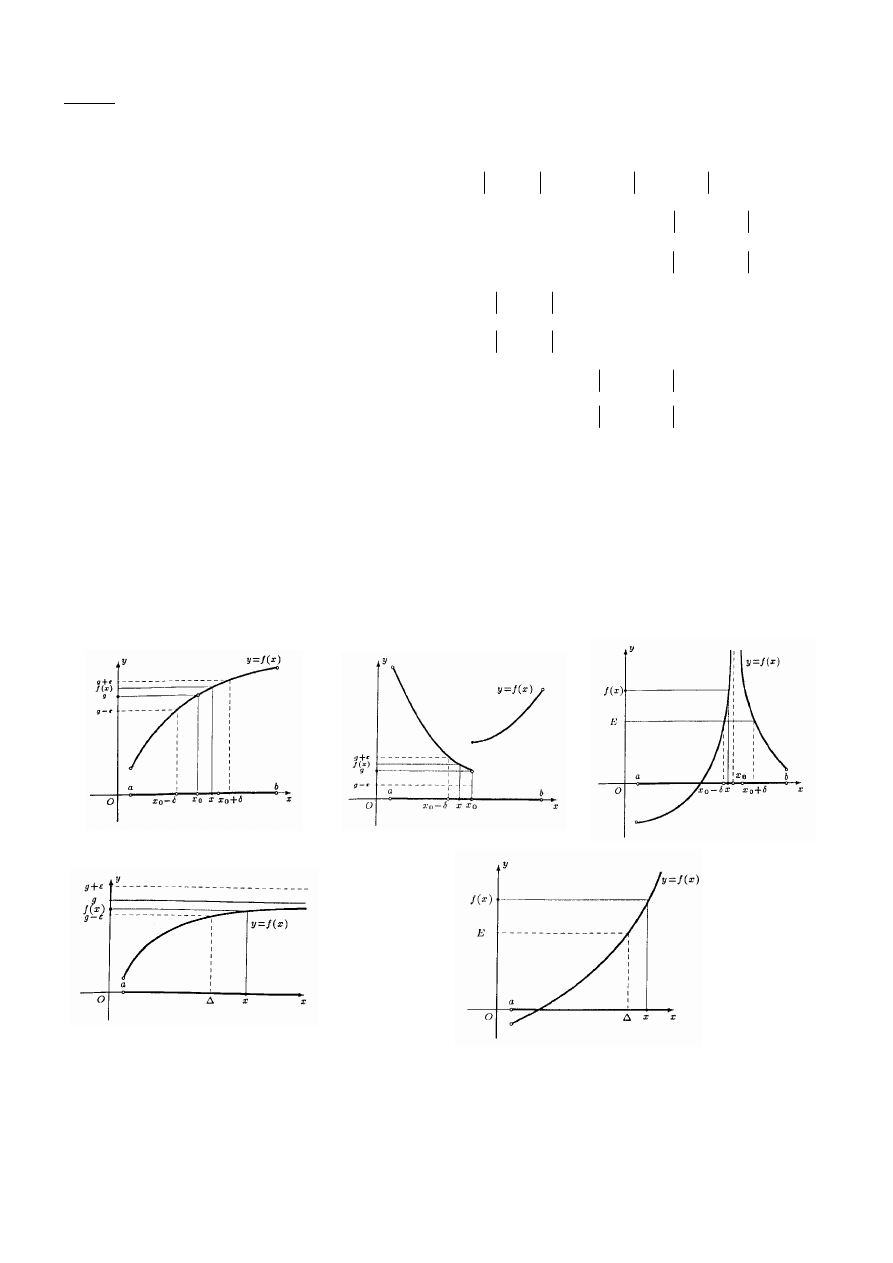
Def.7.5. (granica niewłaściwa funkcji w nieskończoności)
Niech funkcja f będzie określona przynajmniej na
(
)
∞
+
S
.
Wówczas granicę niewłaściwą
∞
+
funkcji f w
∞
+
definiujemy następująco:
( )
(
)
( )
+∞
=
⇒
+∞
=
∞
+
∈
∀
⇔
+∞
=
∞
→
∞
→
+∞
→
n
n
n
n
n
n
x
x
f
x
S
x
x
x
f
lim
lim
,
)
(
lim
Analogicznie definiujemy granicę niewłaściwą ∞
−
funkcji f w ∞
−
.
Rys.5. Granica niewłaściwa funkcji w nieskończoności wg Heinego
Przykłady granic niewłaściwych w nieskończoności:
a)
(
)
(
)
{
}
+∞
=
∞
+
=
+
+∞
→
ln
6
ln
lim
2
x
x
b)
(
)
{
}
−∞
=
∞
−
=
−
−∞
→
10
10
lim
5
x
x
c)
[ ]
+∞
=
=
=
∞
+
−∞
+
−∞
→
5
5
1
5
1
lim
9
2x
x
103
Uwaga: Oprócz definicji granicy funkcji według Heinego istnieje definicja według Cauchy’ego.
Wówczas przy tych samych założeniach co do funkcji f jak w poszczególnych definicjach wg Heinego
mamy:
•
(
)
(
)
[
]
ε
δ
δ
ε
<
−
⇒
<
−
∈
∀
>
∃
>
∀
⇔
=
→
g
x
f
x
x
x
S
x
g
x
f
x
x
)
(
)
(
0
0
)
(
lim
0
0
0
•
(
)
(
)
[
]
ε
δ
δ
ε
<
−
⇒
+
<
<
∈
∀
>
∃
>
∀
⇔
=
+
→
+
g
x
f
x
x
x
x
S
x
g
x
f
x
x
)
(
)
(
0
0
)
(
lim
0
0
0
0
•
(
)
(
)
[
]
ε
δ
δ
ε
<
−
⇒
<
<
−
∈
∀
>
∃
>
∀
⇔
=
−
→
−
g
x
f
x
x
x
x
S
x
g
x
f
x
x
)
(
)
(
0
0
)
(
lim
0
0
0
0
•
(
)
(
)
[
]
ε
δ
δ
ε
>
⇒
<
−
∈
∀
>
∃
>
∀
⇔
+∞
=
→
)
(
)
(
0
0
)
(
lim
0
0
0
x
f
x
x
x
S
x
x
f
x
x
•
(
)
(
)
[
]
ε
δ
δ
ε
−
<
⇒
<
−
∈
∀
>
∃
>
∀
⇔
−∞
=
→
)
(
)
(
0
0
)
(
lim
0
0
0
x
f
x
x
x
S
x
x
f
x
x
•
(
)
(
)
[
]
ε
ε
<
−
⇒
∆
>
+∞
∈
∀
∈
∆
∃
>
∀
⇔
=
+∞
→
g
x
f
x
S
x
g
x
f
x
)
(
)
(
0
)
(
lim
R
•
(
)
(
)
[
]
ε
ε
<
−
⇒
∆
<
−∞
∈
∀
∈
∆
∃
>
∀
⇔
=
−∞
→
g
x
f
x
S
x
g
x
f
x
)
(
)
(
0
)
(
lim
R
•
(
)
(
)
[
]
ε
ε
>
⇒
∆
>
+∞
∈
∀
∈
∆
∃
>
∀
⇔
+∞
=
+∞
→
)
(
)
(
0
)
(
lim
x
f
x
S
x
x
f
x
R
•
(
)
(
)
[
]
ε
ε
−
<
⇒
∆
>
+∞
∈
∀
∈
∆
∃
>
∀
⇔
−∞
=
+∞
→
)
(
)
(
0
)
(
lim
x
f
x
S
x
x
f
x
R
•
(
)
(
)
[
]
ε
ε
>
⇒
∆
<
−∞
∈
∀
∈
∆
∃
>
∀
⇔
+∞
=
−∞
→
)
(
)
(
0
)
(
lim
x
f
x
S
x
x
f
x
R
•
(
)
(
)
[
]
ε
ε
−
<
⇒
∆
<
−∞
∈
∀
∈
∆
∃
>
∀
⇔
−∞
=
−∞
→
)
(
)
(
0
)
(
lim
x
f
x
S
x
x
f
x
R
Poniższe rysunki przedstawiają interpretacje geometryczne niektórych granic funkcji wg Cauchy’ego.
a)
b)
c)
d)
e)
Rys.6. Granice funkcji wg definicji Cauchy’ego:
a) granica właściwa funkcji w punkcie, b) granica właściwa lewostronna funkcji w punkcie,
c) granica niewłaściwa funkcji w punkcie, d) granica właściwa w nieskończoności,
e) granica niewłaściwa w nieskończoności

104
Tw.7.2. (o działaniach arytmetycznych na granicach właściwych funkcji)
Jeżeli
q
x
g
p
x
f
x
x
x
x
=
=
→
→
)
(
lim
,
)
(
lim
0
0
to:
1.
(
)
q
p
x
g
x
f
x
x
±
=
±
→
)
(
)
(
lim
0
;
2.
q
p
x
g
x
f
x
x
⋅
=
⋅
→
)
(
)
(
lim
0
3.
p
x
f
x
x
⋅
α
=
⋅
α
→
)
(
lim
0
,
R
∈
α
(stała);
4.
( )
0
,
dla
0
)
(
,
)
(
)
(
lim
0
0
≠
∈
≠
=
→
q
x
S
x
x
g
q
p
x
g
x
f
x
x
GRANICE PODSTAWOWYCH WYRAŻEŃ NIEOZNACZONYCH
1)
1
sin
lim
0
=
→
x
x
x
2)
1
tg
lim
0
=
→
x
x
x
3)
0
,
ln
1
lim
0
>
=
−
→
a
a
x
a
x
x
4)
1
1
lim
0
=
−
→
x
e
x
x
5)
(
)
1
,
0
,
log
1
log
lim
0
≠
>
=
+
→
a
a
e
x
x
a
a
x
6)
(
)
1
1
ln
lim
0
=
+
→
x
x
x
7)
e
x
x
x
=
+
±∞
→
1
1
lim
8)
R
∈
=
+
±∞
→
a
e
x
a
a
x
x
,
1
lim
9)
e
x
x
x
=
+
→
1
0
)
1
(
lim
10)
(
)
R
∈
=
−
+
→
a
a
x
x
a
x
,
1
1
lim
0
11)
1
arcsin
lim
0
=
→
x
x
x
12)
1
arctg
lim
0
=
→
x
x
x
Tw.7.3. (o granicy funkcji złożonej)
Jeżeli funkcje f i g spełniają warunki:
1)
0
)
(
lim
0
y
x
f
x
x
=
→
;
2)
0
)
(
y
x
f
≠
dla każdego
( )
0
x
S
x ∈
,
3)
g
y
g
y
y
=
→
)
(
lim
0
to
[
]
g
x
f
g
x
x
=
→
)
(
lim
0
.
Przykład: Wykorzystując twierdzenie o granicy funkcji złożonej obliczyć:
a)
(
)
2
4
1
1
lim
−
→
x
x
b)
)
2
(
3
)
2
sin(
lim
2
+
+
−
→
x
x
x
.
Rozwiązanie:
a)
(
)
=
−
→
2
4
1
1
lim x
x
{wykonujemy podstawienie}
=
→
→
=
−
=
0
to
1
1
4
y
x
y
x
0
lim
2
0
=
→
y
y

105
b)
=
+
+
−
→
)
2
(
3
)
2
sin(
lim
2
x
x
x
{wykonujemy podstawienie}
3
1
1
3
1
sin
lim
3
1
0
to
2
2
0
=
⋅
=
=
→
−
→
=
+
=
→
t
t
t
x
t
x
t
CIĄGŁOŚĆ FUNKCJI
Def.7.6. (ciągłość funkcji w punkcie)
Niech funkcja f będzie określona na pewnym otoczeniu punktu
R
∈
0
x
, tj.
( )
0
x
U
.
Funkcję
)
(x
f
nazywamy funkcją ciągłą w punkcie
0
x
, jeśli istnieje jej granica w tym punkcie oraz
zachodzi równość:
( )
0
)
(
lim
0
x
f
x
f
x
x
=
→
Tw.7.4. (o ciągłości sumy, różnicy iloczynu i ilorazu funkcji ciągłych)
Jeżeli funkcje f i g są ciągłe w punkcie
0
x
, to:
1)
funkcje
)
(
)
(
),
(
)
(
x
g
x
f
x
g
x
f
−
+
są ciągłe w punkcie
0
x
2)
funkcja
)
(
)
(
x
g
x
f
⋅
jest ciągła w punkcie
0
x
3)
funkcja
)
(
)
(
x
g
x
f
jest ciągła w punkcie
0
x
, o ile
( )
0
0
≠
x
g
.
Def.7.7. (ciągłość lewostronna i prawostronna)
Niech funkcja f będzie określona na pewnym lewostronnym otoczeniu punktu
R
∈
0
x
, tj.
( )
0
x
U
−
.
Funkcję
)
(x
f
nazywamy funkcją lewostronnie ciągłą w punkcie
0
x
, jeśli istnieje granica lewostronna w
tym punkcie oraz zachodzi równość:
( )
0
)
(
lim
0
x
f
x
f
x
x
=
−
→
Niech funkcja f będzie określona na pewnym prawostronnym otoczeniu punktu
R
∈
0
x
, tj.
( )
0
x
U
+
.
Funkcję
)
(x
f
nazywamy funkcją prawostronnie ciągłą w punkcie
0
x
, jeśli istnieje granica
prawostronna w tym punkcie oraz zachodzi równość:
( )
0
)
(
lim
0
x
f
x
f
x
x
=
+
→
Def.7.8. (ciągłość funkcji na przedziale)
Funkcja
)
(x
f
jest funkcją ciągłą na przedziale
(
)
b
a
,
, jeżeli jest ciągła w każdym punkcie tego
przedziału (tj. w każdym punkcie
)
,
(
0
b
a
x ∈
).
Uwaga: Powyższa definicja pozostaje prawdziwa dla przedziałów:
(
) (
) (
)
+∞
∞
−
+∞
∞
−
,
,
,
,
,
a
a
.
Funkcja
)
(x
f
jest funkcją ciągłą na przedziale
b
a
,
, jeżeli jest ciągła na przedziale
)
,
( b
a
oraz
prawostronnie ciągła w punkcie a i lewostronnie ciągła w punkcie b .
Tw.7.5. (warunek konieczny i dostateczny ciągłości funkcji)
Funkcja
)
(x
f
jest funkcją ciągłą w punkcie
0
x
, wtedy i tylko wtedy, gdy jest lewostronnie i
prawostronnie ciągła w punkcie
0
x
.
106
Tw.7.6. (o ciągłości funkcji elementarnych)
Funkcje elementarne są funkcjami ciągłymi na swoich dziedzinach.
Uwaga: Funkcję, która nie jest funkcją ciągłą w punkcie nazywamy funkcją nieciągłą w tym punkcie.
Natomiast punkt ten nazywamy punktem nieciągłości.
Def.7.9. (punkt nieciągłości I – go rodzaju)
Niech funkcja f będzie określona na pewnym otoczeniu punktu
R
∈
0
x
, tj.
( )
0
x
U
.
Funkcja ma w punkcie
0
x
nieciągłość I – go rodzaju, jeżeli istnieją jednostronne granice właściwe
)
(
lim
0
x
f
x
x
+
→
,
)
(
lim
0
x
f
x
x
−
→
oraz
)
(
)
(
lim
0
0
x
f
x
f
x
x
≠
−
→
lub
)
(
)
(
lim
0
0
x
f
x
f
x
x
≠
+
→
.
Przy czym, jeśli zachodzi warunek:
)
(
lim
)
(
lim
0
0
x
f
x
f
x
x
x
x
+
−
→
→
≠
to mamy do czynienia z punktem nieciągłości I – go rodzaju typu ”skok”;
( )
0
)
(
lim
)
(
lim
0
0
x
f
x
f
x
f
x
x
x
x
≠
=
+
−
→
→
to mamy do czynienia z punktem nieciągłości I – go rodzaju typu
”luka”.
a)
b)
Rys.7. Punkty nieciągłości I – go rodzaju
a) punkt nieciągłości typu „skok”, b) punkt nieciągłości typu „luka”
Def.7.10. (punkt nieciągłości II – go rodzaju)
Niech funkcja f będzie określona na pewnym otoczeniu punktu
( )
0
x
U
.
Funkcja ma w punkcie
0
x
nieciągłość II – go rodzaju, jeżeli przynajmniej jedna z granic jednostronnych
)
(
lim
0
x
f
x
x
+
→
,
)
(
lim
0
x
f
x
x
−
→
jest niewłaściwa lub nie istnieje.
a)
b)
Rys.8. Punkty nieciągłości II – go rodzaju
a) niewłaściwe granice jednostronne funkcji w punkcie, b) nie istnieje lewostronna granica funkcji
0
x
x
y
( )
0
x
f
( )
0
x
f
x
0
x
y

107
Przykład: Dana jest funkcja:
>
−
−
≤
<
+
≤
<
−
+
−
=
−
<
<
−
−
≤
−
=
2
3
3
2
2
2
3
0
2
1
log
0
2
1
2
1
2
7
2
3
5
3
2
)
(
2
1
x
x
x
x
x
x
x
x
x
x
f
x
. Zbadać ciągłość podanej funkcji
oraz określić rodzaj ewentualnych punktów nieciągłości.
Rozwiązanie:
Podana funkcja jest ciągła na zbiorze
−
−
2
3
,
0
,
2
,
3
\
R
na podstawie Tw.7.4 oraz Tw.7.6.
Badamy ciągłość w punktach, w których „zmienia” się wykres funkcji:
1)
3
0
−
=
x
{
}
5
5
lim
)
(
lim
5
)
3
(
2
)
2
(
lim
)
(
lim
3
3
3
3
=
=
=
−
−
=
−
=
+
+
−
−
−
→
−
→
−
→
−
→
x
x
x
x
x
f
x
x
f
czyli
)
(
lim
)
(
lim
3
3
x
f
x
f
x
x
+
−
−
→
−
→
=
więc istnieje
5
)
(
lim
3
=
−
→
x
f
x
5
)
3
(
2
)
3
(
=
−
−
=
−
f
Zatem
)
3
(
)
(
lim
3
−
=
−
→
f
x
f
x
, czyli funkcja jest ciągła w punkcie
3
0
−
=
x
.
2)
2
0
−
=
x
5
1
2
1
1
2
1
lim
)
(
lim
5
5
lim
)
(
lim
2
2
2
2
2
=
+
=
+
=
=
=
−
−
→
−
→
−
→
−
→
+
+
−
−
x
x
x
x
x
x
f
x
f
czyli
)
(
lim
)
(
lim
2
2
x
f
x
f
x
x
+
−
−
→
−
→
=
więc istnieje
5
)
(
lim
2
=
−
→
x
f
x
7
)
2
(
=
−
f
Zatem
)
2
(
)
(
lim
2
−
≠
−
→
f
x
f
x
, czyli w punkcie
2
0
−
=
x
funkcja ma punkt nieciągłości I – go rodzaju typu
„luka”.
3)
0
0
=
x
1
2
1
log
2
1
0
log
2
1
log
lim
)
(
lim
2
1
2
1
1
2
1
lim
)
(
lim
2
1
2
1
2
1
0
0
0
0
0
=
=
+
=
+
=
=
+
=
+
=
+
+
−
−
→
→
→
→
x
x
f
x
f
x
x
x
x
x
czyli
)
(
lim
)
(
lim
0
0
x
f
x
f
x
x
+
−
→
→
≠
więc nie istnieje
)
(
lim
0
x
f
x
→

108
2
1
2
1
)
0
(
0
=
+
=
f
Zatem w punkcie
0
0
=
x
funkcja ma punkt nieciągłości I – go rodzaju typu „skok”. Przy czym skok
funkcji w punkcie wynosi:
1
2
1
)
(
lim
)
(
lim
0
0
−
=
−
=
−
=
−
+
→
→
x
f
x
f
s
x
x
4)
2
3
0
=
x
−∞
=
−
=
−
=
−
−
=
−
−
=
−
=
=
+
=
+
=
+
+
+
→
→
→
→
+
+
−
−
0
2
0
2
3
3
2
3
2
2
lim
)
(
lim
1
2
log
2
1
2
3
log
2
1
log
lim
)
(
lim
2
3
2
3
2
1
2
1
2
1
2
3
2
3
x
x
f
x
x
f
x
x
x
x
więc nie istnieje
)
(
lim
2
3
x
f
x→
1
2
1
2
3
log
3
3
2
1
−
=
+
=
f
Zatem w punkcie
2
3
0
=
x
funkcja ma punkt nieciągłości II – go rodzaju.
Ostatecznie podana funkcja jest ciągła na zbiorze
−
2
3
,
0
,
2
\
R
.
POCHODNA FUNKCJI
Def.7.11. (pochodna funkcji w punkcie)
Niech funkcja f będzie określona na pewnym otoczeniu punktu
R
∈
0
x
, tj.
( )
0
x
U
.
Pochodną właściwą funkcji
w punkcie
0
x
, co oznaczamy
( )
0
x
f ′
, nazywamy granicę właściwą:
(
)
( )
h
x
f
h
x
f
h
0
0
0
lim
−
+
→
czyli
( )
(
)
( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
−
+
=
′
→
.
Uwaga: Jeżeli funkcja ma pochodną w punkcie to mówimy, że jest różniczkowalna w tym punkcie.
Przykład: Na podstawie definicji obliczyć pochodną funkcji
2
2
)
(
x
x
f
=
w punkcie
0
x
.
Rozwiązanie:
Dziedzina tej funkcji to cały zbiór liczb rzeczywistych.
Dla
R
∈
0
x
mamy:
( )
(
)
( )
(
)
0
0
0
0
0
2
0
2
0
2
0
0
2
0
2
0
0
0
0
0
0
4
)
2
4
(
lim
)
2
4
(
lim
2
2
4
2
lim
2
2
lim
lim
x
h
x
h
h
x
h
h
x
h
h
x
x
h
x
h
x
h
x
f
h
x
f
x
f
h
h
h
h
h
=
+
=
=
+
=
−
+
+
=
−
+
=
−
+
=
′
→
→
→
→
→
109
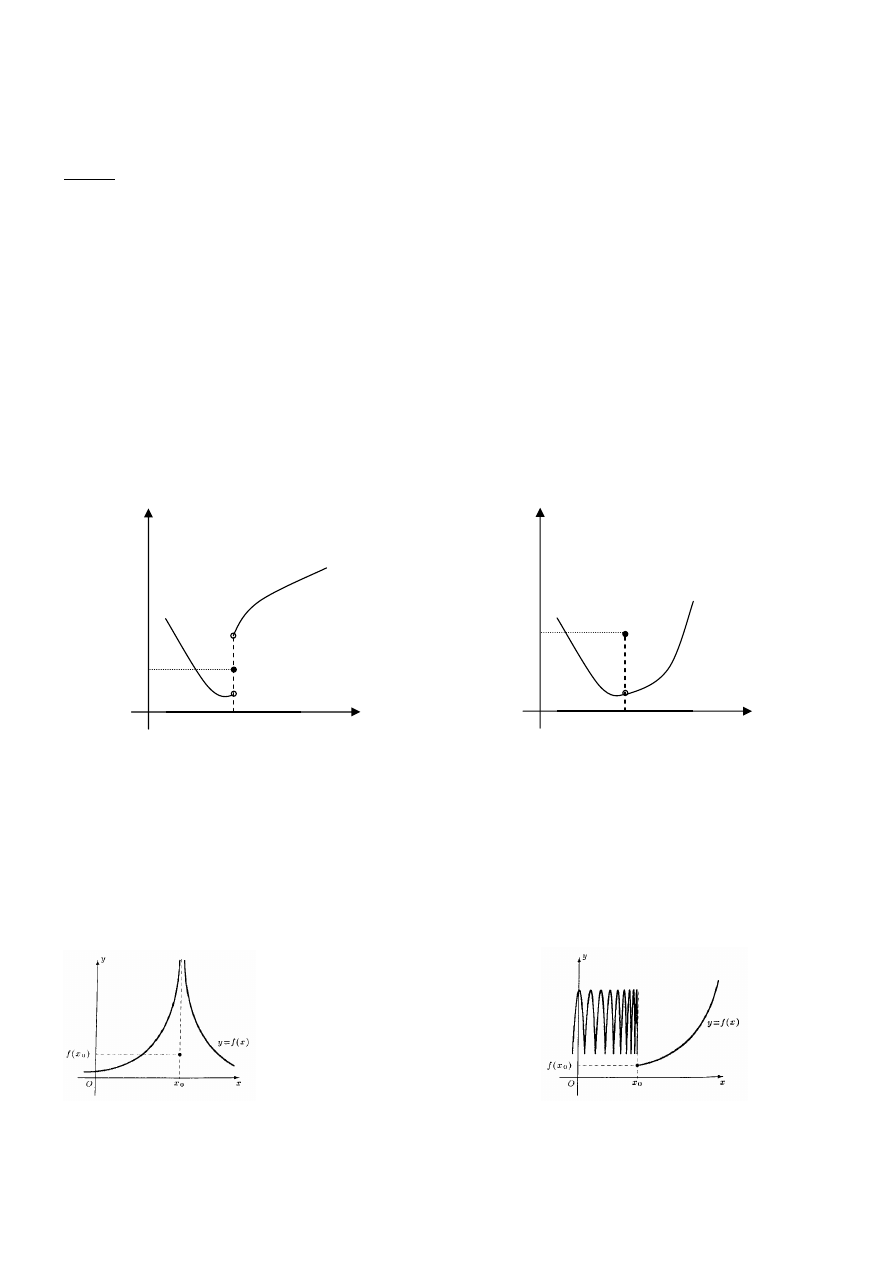
W interpretacji geometrycznej pochodna funkcji w punkcie
0
x
jest równa tangensowi kąta między
styczną do wykresu funkcji w tym punkcie a dodatnią półosią OX, czyli
α
tg
)
(
0
=
′ x
f
.
Rys.9. Interpretacja geometryczna pochodnej funkcji w punkcie
Def.7.12. (pochodne jednostronne funkcji w punkcie)
Niech funkcja f będzie określona na pewnym lewostronnym otoczeniu
( )
0
x
U
−
.
Pochodną właściwą lewostronną
funkcji f w punkcie
0
x
, co oznaczamy
( )
0
x
f
−
′
, nazywamy granicę
właściwą:
( )
(
)
( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
−
+
=
′
−
→
−
Niech funkcja f będzie określona na pewnym prawostronnym otoczeniu
( )
0
x
U
+
.
Pochodną właściwą prawostronną
funkcji f w punkcie
0
x
, co oznaczamy
( )
0
x
f
+
′
, nazywamy granicę
właściwą:
( )
(
)
( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
−
+
=
′
+
→
+
Tw.7.7. (warunek konieczny i dostateczny istnienia pochodnej funkcji w punkcie)
Funkcja f ma pochodną w punkcie
0
x
wtedy i tylko wtedy, gdy
( )
( )
0
0
x
f
x
f
+
−
′
=
′
.
Tw.7.8. (warunek konieczny różniczkowalności funkcji w punkcie)
Jeżeli funkcja jest różniczkowalna w punkcie, to jest ciągła w tym punkcie.
Uwaga: Twierdzenie odwrotne nie jest prawdziwe, co ilustruje poniższy przykład.
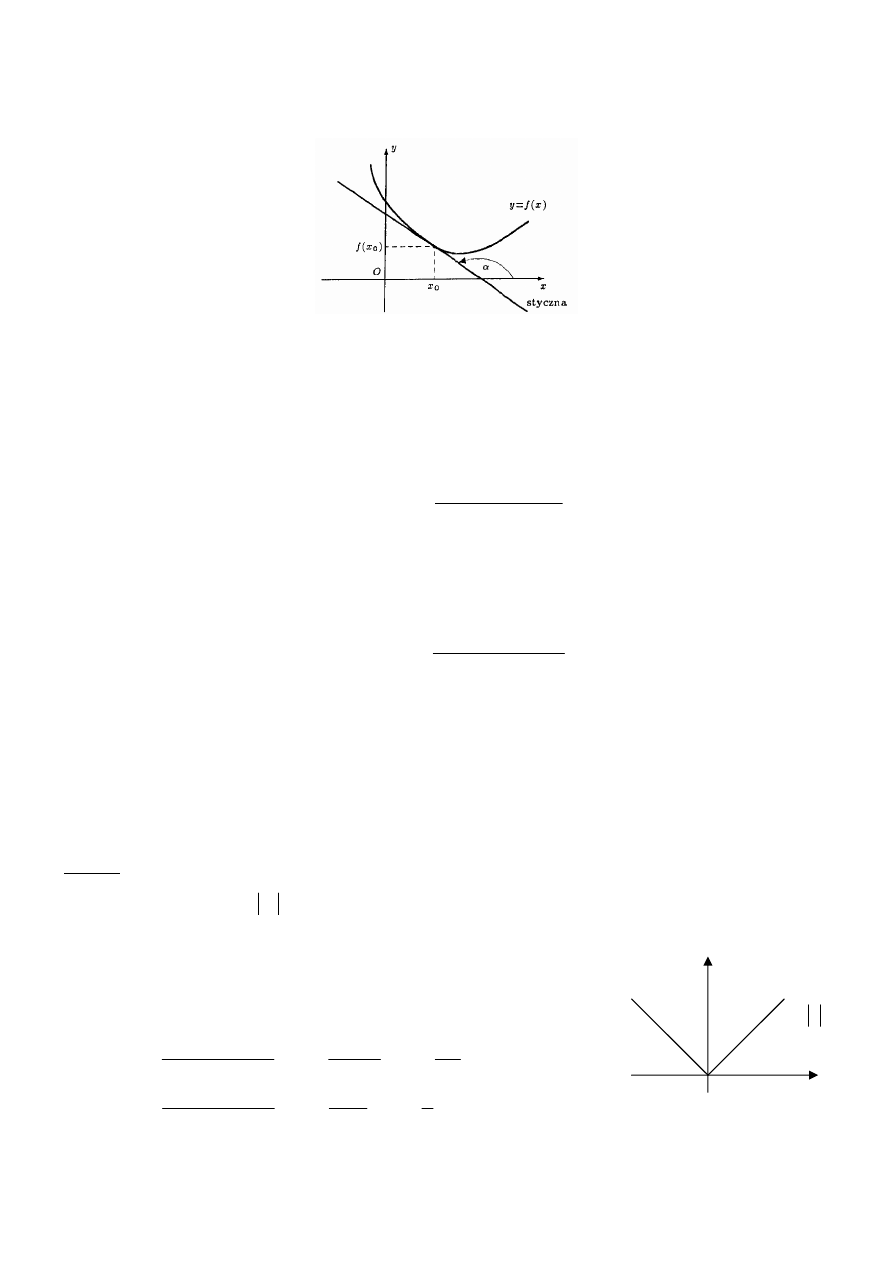
Przykład: Funkcja
x
x
f
=
)
(
jest funkcją ciągłą w punkcie
0
0
=
x
(patrz poniższy rysunek), ale nie jest
różniczkowalna w tym punkcie.
Ponieważ
<
−
≥
=
0
0
)
(
x
x
x
x
x
f
, więc wykres przedstawia się następująco:
Obliczamy pochodne jednostronne:
( )
(
)
( )
( )
(
)
( )
1
lim
0
lim
0
0
lim
0
1
lim
0
lim
0
0
lim
0
0
0
0
0
0
0
=
=
−
=
−
+
=
′
−
=
−
=
−
−
=
−
+
=
′
+
+
+
−
−
−
→
→
→
+
→
→
→
−
h
h
h
h
h
f
h
f
f
h
h
h
h
h
f
h
f
f
h
h
h
h
h
h
Ponieważ
( )
( )
0
0
+
−
′
≠
′
f
f
, zatem nie istnieje pochodna
( )
0
f ′
.
y
x
x
y =

110
Def.7.13. (pochodna funkcji na zbiorze)
Funkcja ma pochodną właściwą na zbiorze wtedy i tylko wtedy, gdy ma pochodną właściwą w każdym
punkcie zbioru.
Tw.7.9. (o pochodnej sumy, różnicy, iloczynu oraz ilorazu funkcji)
Jeżeli funkcje f i g są różniczkowalne w punkcie
0
x
,
R
∈
c
jest pewną stałą, to:
1)
( )
( )
[
]
( )
( )
0
0
0
0
x
g
x
f
x
g
x
f
′
±
′
=
′
±
2)
( )
[
]
( )
0
0
x
f
c
x
f
c
′
⋅
=
′
⋅
3)
( ) ( )
[
]
( ) ( )
( )
( )
0
0
0
0
0
0
x
g
x
f
x
g
x
f
x
g
x
f
′
⋅
+
⋅
′
=
′
⋅
4)
( )
( )
( ) ( )
( )
( )
( )
( )
0
,
0
0
2
0
0
0
0
0
0
≠
′
⋅
−
⋅
′
=
′
x
g
x
g
x
g
x
f
x
g
x
f
x
g
x
f
POCHODNE WAŻNIEJSZYCH FUNKCJI ELEMENTARNYCH
1.
( )
R
∈
=
′
C
C
,
0
, C – const.
2.
( )
0
,
,
1
>
∈
α
α
=
′
−
α
α
x
x
x
R
Pochodne funkcji trygonometrycznych
3.
(
)
R
∈
=
′
x
x
x
,
cos
sin
4.
(
)
R
∈
−
=
′
x
x
x
,
sin
cos
5.
(
)
Z
∈
+
≠
=
′
k
k
x
x
x
,
2
,
cos
1
tg
2
π
π
6.
(
)
Z
∈
≠
−
=
′
k
k
x
x
x
,
,
sin
1
ctg
2
π
Pochodna funkcji wykładniczej
7.
( )
1
,
0
,
,
ln
≠
>
∈
=
′
a
a
x
a
a
a
x
x
R
8.
( )
R
∈
=
′
x
e
e
x
x
,
Pochodna funkcji logarytmicznej
9.
(
)
0
,
0
,
1
,
ln
1
log
>
>
≠
=
′
x
a
a
a
x
x
a
10.
(
)
0
,
1
ln
>
=
′
x
x
x
Pochodne funkcji cyklometrycznych
11.
(
)
1
,
1
1
arcsin
2
<
−
=
′
x
x
x
12.
(
)
1
,
1
1
arccos
2
<
−
−
=
′
x
x
x
13.
(
)
R
∈
+
=
′
x
x
x
,
1
1
arctg
2
14.
(
)
R
∈
+
−
=
′
x
x
x
,
1
1
arcctg
2
Pochodne funkcji hiperbolicznych
15.
(
)
R
∈
=
′
x
x
x
,
ch
sh
16.
(
)
R
∈
=
′
x
x
x
,
sh
ch
17.
(
)
R
∈
=
′
x
x
x
,
ch
1
th
2
18.
(
)
0
,
sh
1
cth
2
≠
−
=
′
x
x
x
111
Tw.7.10. (o pochodnej funkcji złożonej)
Jeżeli funkcja f ma pochodną w punkcie
0
x
, funkcja g ma pochodną w punkcie
( )
0
x
f
, to
( )
(
)
[
]
( )
(
)
( )
0
0
0
x
g
x
g
f
x
g
f
′
⋅
′
=
′
Przykład: Obliczyć pochodne podanych funkcji we wskazanych punktach:
a)
R
∈
=
0
2
sin
)
(
x
x
x
h
Ponieważ
(
)
2
sin
)
(
x
x
h
=
, więc funkcją zewnętrzną jest funkcja kwadratowa
( )
(
)
[
]
2
)
(x
g
x
g
f
=
, natomiast
x
x
g
sin
)
( =
jest funkcją wewnętrzną.
Zatem
(
)
[
]
0
0
0
0
0
2
0
0
2
sin
cos
sin
2
)
(sin
sin
2
sin
)
(
x
x
x
x
x
x
x
h
=
=
′
⋅
=
′
=
′
b)
(
)
+∞
∈
=
,
0
)
(
0
cos
x
e
x
h
x
Mamy tutaj do czynienia z funkcją trzykrotnie złożoną: funkcją zewnętrzną jest funkcja eksponent,
następnie funkcją wewnętrzną – cosinus, a na końcu funkcja pierwiastkowa.
Obliczamy pochodną:
(
)
(
)
(
) (
)
0
cos
0
0
0
cos
0
cos
cos
0
2
1
sin
sin
cos
)
(
0
0
0
0
x
e
x
x
x
e
x
e
e
x
h
x
x
x
x
⋅
⋅
−
=
′
⋅
−
⋅
=
′
⋅
=
′
=
′
c)
4
2
2
1
1
)
(
+
−
=
x
x
x
h
,
R
∈
x
Wówczas
(
) (
) (
) (
)
(
)
(
) (
)
(
)
(
)
(
)
(
)
(
)
5
2
3
2
2
2
3
2
2
2
2
3
2
2
2
2
2
2
3
2
2
2
2
2
2
2
2
3
2
2
2
2
3
2
2
4
2
2
1
1
16
1
16
1
1
1
4
1
1
4
1
2
1
1
2
1
1
4
1
1
1
1
1
1
1
4
1
1
1
1
4
1
1
)
(
+
−
=
=
+
⋅
+
−
=
+
⋅
+
−
⋅
=
+
⋅
−
−
+
⋅
⋅
+
−
⋅
=
=
+
′
+
⋅
−
−
+
⋅
′
−
⋅
+
−
⋅
=
′
+
−
⋅
+
−
⋅
=
′
+
−
=
′
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
h
Def.7.14. (pochodna właściwa n – tego rzędu funkcji)
Pochodną właściwą n – tego rzędu
funkcji f w punkcie
0
x
definiujemy następująco:
( )
( )
[
]
′
=
−
0
)
1
(
0
)
(
x
f
x
f
n
n
dla
2
≥
n
przy czym
( )
( )
0
0
)
1
(
x
f
x
f
′
=
;
( )
( )
0
0
)
0
(
x
f
x
f
=
Zatem np.
( )
( )
[
]
′
′
=
′′
0
0
x
f
x
f
;
( )
( )
[
]
′
′′
=
′′
′
0
0
x
f
x
f
; itd.

112
Przykład: Obliczyć y ′′′ , jeśli
x
x
y
ln
=
.
0
>
x
Rozwiązanie:
Obliczamy pochodną pierwszego rzędu korzystając ze wzoru na pochodną iloczynu:
(
)
(
)
1
ln
1
ln
1
ln
ln
ln
+
=
⋅
+
⋅
=
′
⋅
+
⋅
′
=
′
⋅
=
′
x
x
x
x
x
x
x
x
x
x
y
Obliczamy pochodną drugiego rzędu:
( )
(
)
(
)
x
x
x
y
y
1
ln
0
ln
1
=
′
+
=
′
+
=
′
′
=
′′
Obliczamy pochodną trzeciego rzędu:
( )
2
1
1
x
x
y
y
−
=
′
=
′
′′
=
′′
′
Def.7.15. (różniczka funkcji)
Niech funkcja f ma pochodną w punkcie
0
x
. Różniczką funkcji f w punkcie
0
x
ze względu na przyrost h
(
0
x
x
h
−
=
) nazywamy iloczyn
( )
h
x
f
⋅
′
0
i oznaczamy
( )
0
x
df
, tzn.:
( )
( )
h
x
f
x
df
⋅
′
=
0
0
Przykład: Różniczka funkcji
3
)
(
x
x
f
=
w punkcie
R
∈
x
dla przyrostu h zmiennej niezależnej wynosi:
h
x
dx
x
df
2
3
3
)
(
=
=
.
Natomiast dla funkcji
x
x
f
=
)
(
mamy
h
dx
x
df
=
=
)
(
, czyli różniczka zmiennej niezależnej jest równa
przyrostowi tej zmiennej.
Stąd otrzymujemy:
dx
x
f
x
df
)
(
)
(
′
=
, więc
dx
x
df
x
f
)
(
)
(
=
′
.
Zastosowanie różniczki do obliczeń przybliżonych
Jeżeli funkcja f ma pochodną w punkcie
0
x
, to
h
x
f
x
f
h
x
f
)
(
)
(
)
(
0
0
0
′
+
≈
+
Przykład: Obliczyć przybliżoną wartość:
02
,
1
ln
.
Rozwiązanie:
x
x
f
ln
)
(
=
,
02
,
1
0
=
+ h
x
czyli
02
,
0
,
1
0
=
=
=
dx
h
x
.
Obliczamy
( )
0
1
ln
)
1
(
0
=
=
= f
x
f
oraz
( )
0
0
1
x
x
f
=
′
, czyli
( )
1
1 =
′
f
.
Zatem
02
,
0
1
0
02
,
1
ln
⋅
+
≈
, stąd
02
,
0
02
,
1
ln
≈
RÓWNANIE STYCZNEJ I NORMALNEJ
Równanie stycznej do wykresu funkcji f w punkcie
(
)
)
(
,
0
0
0
x
f
x
P
ma postać:
)
)(
(
)
(
0
0
0
x
x
x
f
x
f
y
−
′
=
−
.
Równanie normalnej do wykresu funkcji f w punkcie
(
)
)
(
,
0
0
0
x
f
x
P
ma postać:
)
(
)
(
1
)
(
0
0
0
x
x
x
f
x
f
y
−
′
−
=
−
, gdzie
0
)
(
0
≠
′ x
f
.
Wyszukiwarka
Podobne podstrony:
13 GRANICA CIAGLOSC POCHODNA, szkola technikum, matma, mata, zadania z liceum
lista7 granica, ciaglosc i pochodna funkcji
Microsoft Word W16 pochodne zlozone funkcji 2 zm
Microsoft Word L16 pochodne f zlozonej 2 zmiennych
5 Ciagi,granica i ciaglosc funkcji
Microsoft Word W14 Szeregi Fouriera
New Microsoft Word Document (2)
Nowy Dokument programu Microsoft Word (5)
Nowy Dokument programu Microsoft Word
Nowy Dokument programu Microsoft Word
granice ciągłość
Granica i ciągłość funkcji
Microsoft Word zrodla infor I czesc pprawiona 2 do wydr
2011 Granice Ciaglosc Cwiczenia 3id 27561
Przed maturą Zestaw XI Ciągłość i pochodna funkcji
Granica i ciągłość funkcji zadania
więcej podobnych podstron