WYKŁAD PLENARNY

Kwantowe splątanie dwóch atomów

∗

Ryszard Tanaś

Instytut Fizyki, Uniwersytet im. Adama Mickiewicza, Poznań

Quantum entanglement of two atoms

Abstract: Evolution of quantum entanglement in a system of two two-level atoms undergoing
spontaneous emission to the vacuum modes is discussed.

Wstęp

Jednym z najbardziej fascynujących i tajemniczych

zjawisk w mechanice kwantowej jest zjawisko splątania
kwantowego. W słynnej pracy z 1935 r. Einstein, Podolsky
i Rosen [1] starali się wykazać, że mechanika kwantowa
musi być niekompletna, skoro przewiduje istnienie korela-
cji kwantowych na dużych odległościach. Dzisiaj możemy
powiedzieć, że nie mieli racji, a korelacje kwantowe, któ-
rych istnienie kwestionowali, istnieją naprawdę i są po-
twierdzone licznymi eksperymentami. Na to, by mówić
o splątaniu kwantowym, bo tak dzisiaj zwykle nazywamy
istnienie tych tajemniczych korelacji kwantowych, trzeba
układu kwantowego złożonego z dwóch podukładów. Zna-
komitym przykładem takiego układu są dwa atomy, które
mogą znaleźć się w stanie splątanym w wyniku sprzę-
żenia poprzez próżnię fotonową. Sprzężenie takie prowa-
dzi do kolektywnego zachowania się dwóch atomów, ob-
jawiającego się oddziaływaniem typu dipol–dipol między
nimi oraz kolektywną emisją spontaniczną. Celem niniej-
szego artykułu jest przybliżenie mechanizmu powstawa-
nia i ewolucji stanów splątanych w układzie dwóch ato-
mów.

Ewolucja dwóch atomów

Jednym z najbardziej popularnych modeli optyki

kwantowej jest model a t o m u d w u p o z i o m o w e g o.
W modelu tym przyjmujemy, że atom jest układem
o dwóch tylko stanach kwantowych: stanie podstawowym
i stanie wzbudzonym. Jest to oczywiście dość drastyczne
uproszczenie opisu rzeczywistego atomu, ale w wielu sy-
tuacjach fizycznych atom dwupoziomowy jest bardzo do-
brym przybliżeniem, znakomicie oddającym istotę opisy-
wanych zjawisk fizycznych. Zaletą tego modelu jest to, że
jest on wyjątkowo prosty i jego ewolucję potrafimy opisać
dość dokładnie. Z dzisiejszego punktu widzenia taki układ
dwustanowy to k u b i t, czyli bit kwantowy, reprezentujący
jednostkę kwantowej informacji. Natomiast dwa atomy to,
używając terminologii informatyki kwantowej, dwukubi-

towy rejestr kwantowy. Poznanie jego ewolucji jest sprawą
interesującą.

Badania ewolucji układu dwóch atomów dwupo-

ziomowych były prowadzone w latach osiemdziesiątych
ubiegłego wieku (obszerny spis literatury można znaleźć
w pracy przeglądowej [2]). Znaczący udział w nich mieli
Zbigniew Ficek oraz autor niniejszego artykułu. Istotnym
elementem tych badań był fakt, że dwa atomy, które znaj-
dują się w odległości mniejszej niż długość fali światła
emitowanego przez pojedynczy atom, zachowują się ko-
lektywnie, co oznacza, że ewolucja układu dwóch atomów
różni się istotnie od ewolucji atomu pojedynczego. Atomy
przestają być niezależne. Ewolucja układu dwóch atomów
opisywana jest odpowiednim równaniem głównym (ang.
master equation), którego nie będę tutaj przytaczał (patrz
np. [2]). Z równania tego wynika, że jeśli przyjmiemy, że
atomy znajdują się w pewnej stałej odległości r

12

, mniej-

szej od długości fali związanej z przejściem atomowym,
to pojawia się między nimi sprzężenie, które na małych
odległościach ma charakter sprzężenia typu dipol–dipol
(zależność od odległości jest jak r

−3

12

). Pojawia się też

kolektywny parametr modyfikujący emisję spontaniczną
z takiego układu. Rysunek 1 przedstawia dwa identyczne
atomy o stanach {|g

1

i, |e

1

i} oraz {|g

2

i, |e

2

i} i częstości przej-

ścia atomowego ω

0

, które są sprzężone przez oddziaływa-

nie dipol–dipol, oznaczone Ω

12

. Zarówno Ω

12

jak i tłu-

mienie kolektywne Γ

12

zależą od odległości r

12

między

atomami (rys. 2). Widać tutaj, że dla małych odległości
między atomami Ω

12

wyraźnie rośnie, zaś Γ

12

zbliża się

do wartości współczynnika Einsteina dla emisji sponta-
nicznej z pojedynczego atomu Γ.

Przedstawiony tu obraz układu dwóch atomów nie jest

zbyt klarowny. Stany atomowe to stany własne izolowa-
nych atomów, ale oddziaływanie dipol–dipol sprzęga oba
atomy, co powoduje zmianę struktury poziomów. Można
zadać pytanie: w jaki sposób? Bez napisania odpowiednich
równań nie jest też jasne, jaką rolę odgrywa tłumienie ko-
lektywne Γ

12

.

∗

Na podstawie wykładu wygłoszonego podczas XXXVIII Zjazdu Fizyków Polskich w Warszawie (wrzesień 2005) z okazji

otrzymania Nagrody im. Wojciecha Rubinowicza.

104

POSTĘPY FIZYKI

TOM 57

ZESZYT 3

ROK 2006

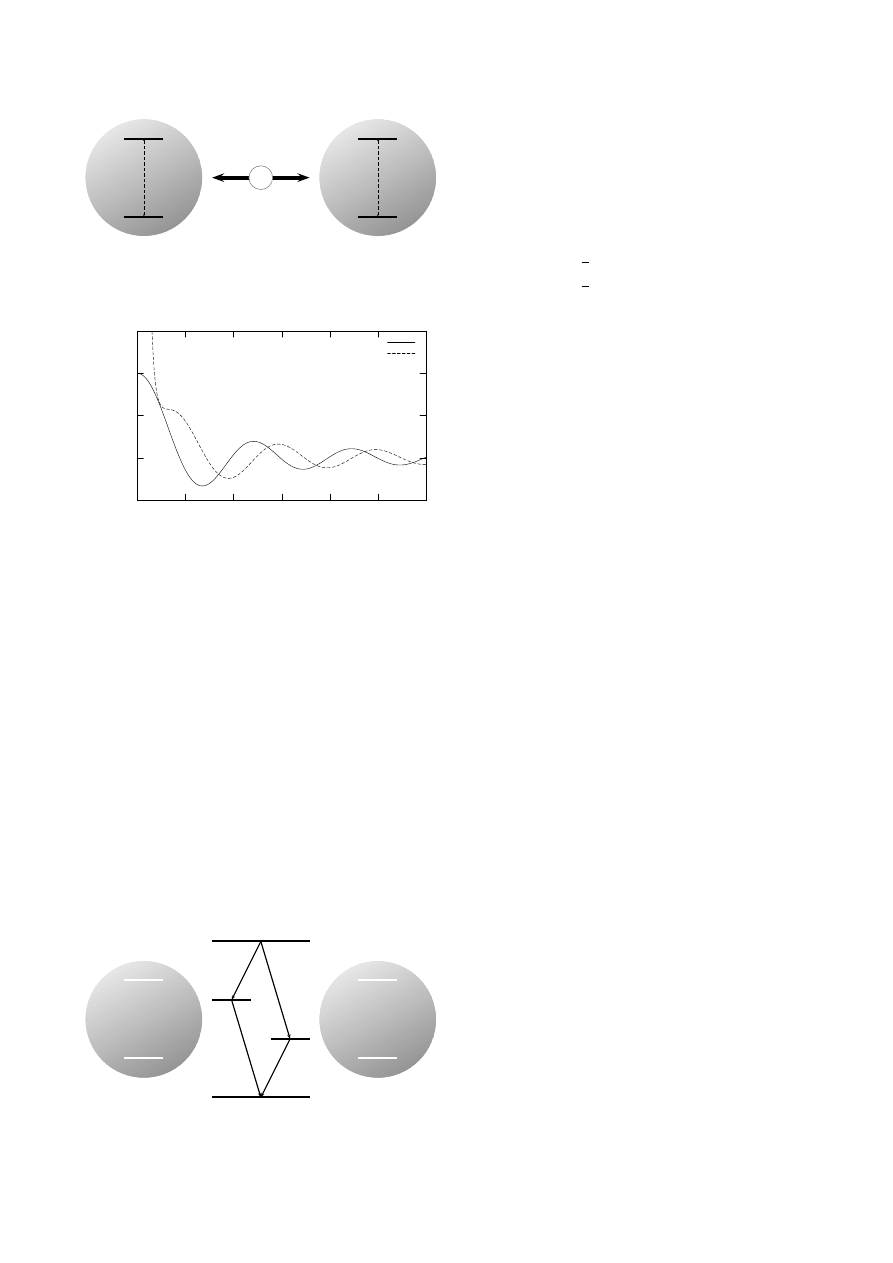
R. Tanaś – Kwantowe splątanie dwóch atomów

|e

1

i

|g

1

i

ω

0

|e

2

i

|g

2

i

ω

0

Ω

12

Rys. 1. Dwa atomy oraz oddziaływanie dipol–dipol między

nimi

−

0

,5

0

0

,5

1

1

,5

0

0

,5

1

1

,5

2

2

,5

3

Γ

12

/

Γ

,

Ω

12

/

Γ

r

12

/λ

Γ

12

Ω

12

Rys. 2. Zależność parametrów kolektywnych Γ

12

oraz Ω

12

od odległości r

12

między atomami. Zakładamy, że momenty

przejścia w obu atomach są równoległe, a przy tym prostopa-

dłe do linii łączącej atomy ( ˆ

µ ⊥ ˆr

12

).

Stany kolektywne

Obraz naszego układu staje się znacznie bardziej

przejrzysty, jeśli wprowadzimy s t a n y k o l e k t y w n e.
Jeśli oddziaływanie dipol–dipol włączymy do układu
dwóch atomów i znajdziemy stany własne takiego roz-
szerzonego układu, to obraz wygląda tak jak na rys. 3.
Zniknęły stany własne izolowanych atomów i pojawiły się
nowe stany, które nazywamy stanami kolektywnymi, opi-
sujące układ dwóch atomów wraz z oddziaływaniem. Na
rysunku 3 pozostały jeszcze atomy z cieniami ich stanów,
aby przypominać, że ciągle mamy do czynienia z dwoma
atomami, ale układ jest teraz reprezentowany przez nowe
stany, których schemat widzimy pomiędzy atomami.

|ei

|gi

|si

|ai

|e

1

i

|g

1

i

|e

2

i

|g

2

i

Γ + Γ

12

Γ + Γ

12

Γ

− Γ

12

Γ

− Γ

12

Rys. 3. Stany kolektywne układu dwóch atomów oraz dwa

kanały emisji spontanicznej

O ile w poprzednim obrazie układu dwóch atomów

bazę wyznaczały stany własne izolowanych atomów

{|g

1

i ⊗ |g

2

i,

|e

1

i ⊗ |e

2

i,

|g

1

i ⊗ |e

2

i,

|e

1

i ⊗ |g

2

i},

to w stanach kolektywnych bazę wyznaczają stany

{|gi = |g

1

i ⊗ |g

2

i,

|ei = |e

1

i ⊗ |e

2

i,

|si = (1/

√

2) (|e

1

i ⊗ |g

2

i + |g

1

i ⊗ |e

2

i) ,

|ai = (1/

√

2) (|e

1

i ⊗ |g

2

i − |g

1

i ⊗ |e

2

i)}.

Pojawiły się tutaj dwa nowe stany: symetryczny |si i anty-
symetryczny |ai, które są superpozycjami stanów iloczy-
nowych. Stanów tych nie da się przedstawić w postaci
iloczynów stanów jednoatomowych. Są to, jak mówimy,
stany m a k s y m a l n i e s p l ą t a n e lub mówiąc inaczej
– s t a n y B e l l a. To właśnie tego typu stany tak niepo-
koiły Einsteina, Podolsky’ego i Rosena. Tutaj takie stany
pojawiły się niejako w sposób naturalny, jako stany własne
układu: dwa atomy + oddziaływanie typu dipol–dipol.

Na rysunku 3 przedstawiono także dwa kanały, któ-

rymi może zachodzić emisja spontaniczna. Jeden z nich,
prowadzący przez stan symetryczny |si, jest kanałem
„szybkim”, którym emisja spontaniczna zachodzi w tem-
pie Γ + Γ

12

. Natomiast drugi, prowadzący przez stan an-

tysymetryczny |ai, jest kanałem „wolnym”, o tempie emi-
sji spontanicznej równym Γ − Γ

12

. Ponieważ dla małych

odległości między atomami Γ

12

może być bliskie Γ, stan

antysymetryczny |ai „wyświeca” się znacznie wolniej niż
stan symetryczny |si. A pamiętajmy, że jest to stan mak-
symalnie splątany. Odstęp (w skali częstości) między sta-
nem symetrycznym i antysymetrycznym wynosi 2Ω

12

. Je-

śli Ω

12

> Γ, to stany te są dobrze rozdzielone i istnieje

możliwość przygotowania układu w jednym z nich, a więc
w jednym ze stanów splątanych. Oczywiście, obsadzenie
stanu symetrycznego będzie zanikać wykładniczo ze stałą
zaniku Γ + Γ

12

, zaś stanu antysymetrycznego – ze stałą

zaniku Γ − Γ

12

. Tak więc układ przygotowany w stanie

czystym – maksymalnie splątanym – będzie w czasie ewo-
lucji przechodził do stanu mieszanego. Jaki będzie stopień
splątania takiego stanu? Jak będzie wyglądała ewolucja
układu, jeśli początkowo tylko jeden z atomów jest wzbu-
dzony? Wtedy na początku splątania nie ma; czy w trakcie
ewolucji pojawi się splątanie i jak ono samo będzie ewolu-
owało? Czy pojawi się splątanie, jeśli początkowo obydwa
atomy są wzbudzone? Na wszystkie te pytania potrafimy
odpowiedzieć, a szczegółowe odpowiedzi można znaleźć
w pracy [3]. Tutaj zilustruję tylko niektóre wyniki.

Jak mierzyć stopień splątania?

Aby odpowiedzieć na wcześniej zadane pytania do-

tyczące ewolucji stopnia splątania w układzie dwóch ato-
mów, trzeba wpierw zdefiniować, co to jest „stopień splą-
tania”. O ile w przypadku stanów czystych sprawa jest
prosta, to w przypadku stanów mieszanych, a więc takich,
które musimy opisywać macierzą gęstości, sprawa jest bar-
dziej złożona. Istnieje kilka różnych miar splątania, które

POSTĘPY FIZYKI

TOM 57

ZESZYT 3

ROK 2006

105

R. Tanaś – Kwantowe splątanie dwóch atomów

dają dla stanów mieszanych różne stopnie splątania. Nie
wdając się w dyskusję nad tym, która z tych miar jest lep-
sza i czy istnieje najlepsza miara splątania, zilustrujemy
ewolucję stopnia splątania w układzie dwóch atomów, ko-
rzystając z dwóch znanych i łatwych do obliczenia miar
splątania. Jedną z takich miar jest z g o d n o ś ć czy też
w s p ó ł b i e ż n o ś ć (ang. concurrence). Miara ta, wpro-
wadzona przez Woottersa [4], zdefiniowana jest poprzez
wartości własne pewnej macierzy, skonstruowanej w spe-
cjalny sposób z macierzy gęstości opisującej stan układu.
Dla układu dwóch atomów jest to macierz 4×4; obliczenie
dla niej wartości własnych nie stanowi problemu (pomijam
tutaj szczegóły techniczne, które można znaleźć w orygi-
nalnej literaturze). W niniejszym artykule będziemy ozna-
czali przez C(t) (od concurrence) stopień splątania mie-
rzony poprzez z g o d n o ś ć. Wielkość ta przyjmuje war-
tości od zera do jedności, 0 6 C 6 1, przy czym zero
oznacza brak splątania, a jeden – splątanie maksymalne.
Wartości pośrednie oznaczają splątanie częściowe, którego
stopień określa właśnie wartość C.

Inną miarą splątania kwantowego jest u j e m n o ś ć

(ang. negativity). Miara ta oparta jest na kryterium splą-
tania wprowadzonym przez Peresa [5] i Horodeckich [6].
Tym razem obliczanie stopnia splątania polega na znalezie-
niu ujemnych wartości własnych (stąd „ujemność”) pewnej
macierzy 4 × 4, innej niż w przypadku zgodności, otrzy-
manej z macierzy gęstości opisującej układ dwóch atomów
przez transpozycję względem indeksów jednego z atomów
(znowu pomijam szczegóły). Tę miarę będziemy oznaczali
przez N(t) (od negativity). Podobnie jak C, miara N przyj-
muje wartości z przedziału od zera do jedności, 0 6 N 6 1
(zero – brak splątania, jeden – maksymalne splątanie). Jak
jednak zobaczymy, dla częściowego splątania stopień splą-
tania mierzony wartościami N jest inny niż stopień splą-
tania mierzony wartościami C, chociaż splątanie pojawia
się oczywiście dla tych samych czasów.

Kwantowe splątanie dwóch atomów

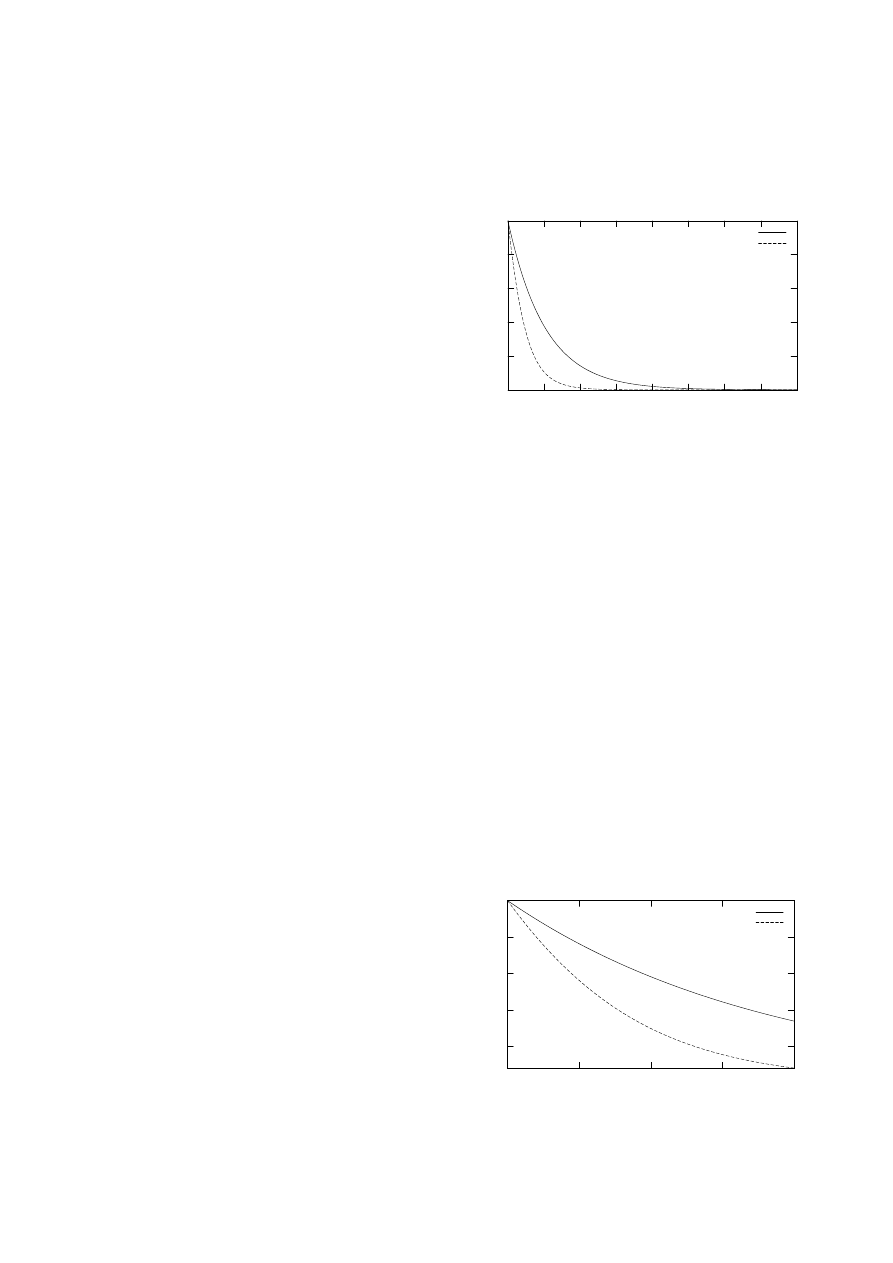
Przyjrzyjmy się zatem, jak ewoluuje stopień splątania

mierzony wartościami C oraz N w rozważanym przez nas
układzie dwóch atomów. Na początek załóżmy, że układ
został przygotowany w chwili t = 0 w stanie symetrycz-
nym |si. Jest to stan maksymalnie splątany, więc począt-
kowo C = N = 1. Z biegiem czasu jednak stopień spląta-
nia maleje (rys. 4). Czas mierzony jest w jednostkach Γ

−1

,

czyli w jednostkach czasu życia stanu wzbudzonego poje-
dynczego atomu. Odległość r

12

między atomami dla tego

rysunku wynosi λ/12, co oznacza, że Γ

12

= 0,95 Γ. Z ry-

sunku widać, że ujemność N(t) zanika szybciej niż zgod-
ność C(t). Interesującym wynikiem jest w tym przypadku
to, że zgodność C(t) zanika wykładniczo w tempie Γ + Γ

12

,

dokładnie tak, jak obsadzenie ρ

ss

(t) stanu symetrycznego.

Jeśli więc przygotujemy układ w stanie maksymalnie splą-
tanym |si i pozwolimy mu się „wyświecać” w procesie
emisji spontanicznej, to ewolucja zgodności przebiega do-
kładnie tak, jak obsadzenia tego stanu. Zachowanie się
ujemności jest bardziej skomplikowane i zależy także od

obsadzenia stanu podstawowego, do którego ucieka popu-
lacja atomowa. Dla obydwu miar splątania możemy napi-
sać analityczne wzory opisujące ewolucję [3], co daje nam
bezpośredni wgląd w fizykę splątania kwantowego.

0

0,2

0,4

0,6

0,8

1

0

0,5

1

1,5

2

2,5

3

3,5

4

st

o

p

ie

ń

sp

lą

ta

n

ia

Γt

C(t)

N (t)

Rys. 4. Ewolucja układu dwóch atomów przygotowanych

w stanie symetrycznym |si przy r

12

= λ/12 (Γ

12

= 0,95 Γ)

Jeśli w chwili t = 0 układ znajduje się w stanie an-

tysymetrycznym |ai, który podobnie jak stan symetryczny
jest stanem maksymalnie splątanym, to mamy do czynie-
nia z sytuacją analogiczną jak dla stanu symetrycznego,
z jedną wszakże istotną różnicą – w tym przypadku emi-
sja spontaniczna zachodzi w tempie Γ − Γ

12

, czyli znacz-

nie wolniej. Taka sytuacja jest zilustrowana na rys. 5 dla
parametrów identycznych jak na rys. 4. Skala czasowa na
rys. 5 została rozciągnięta pięciokrotnie. Ewolucja C(t) od-
powiada tym razem wykładniczemu zanikowi obsadzenia
stanu antysymetrycznego |ai w tempie Γ − Γ

12

. A więc

C(t) = ρ

aa

(t), podobnie jak dla stanu symetrycznego, ale

tym razem zanik jest znacznie wolniejszy. Oznacza to, że
splątanie kwantowe przygotowane w stanie antysymetrycz-
nym przetrwa znacznie dłużej niż splątanie przygotowane
w stanie symetrycznym. Oczywiście w obu przypadkach
układ znajdzie się ostatecznie w stanie podstawowym, ale
gdy startujemy ze stanu antysymetrycznego, mamy znacz-
nie więcej czasu na wykonanie operacji na takim rejestrze
kwantowym. Także ujemność w tym przypadku zanika

0,2

0,4

0,6

0,8

1

0

5

10

15

20

st

o

p

ie

ń

sp

lą

ta

n

ia

Γt

C(t)

N (t)

Rys. 5. Ewolucja układu dwóch atomów przygotowanych
w stanie antysymetrycznym |ai przy r

12

= λ/12 (Γ

12

= 0,95 Γ)

106

POSTĘPY FIZYKI

TOM 57

ZESZYT 3

ROK 2006

R. Tanaś – Kwantowe splątanie dwóch atomów

w tempie wolniejszym, chociaż ciągle znacznie szybciej
niż zgodność.

Z innym ciekawym przypadkiem mamy do czynie-

nia, gdy stan początkowy został przygotowany w taki spo-
sób, że tylko jeden z atomów jest wzbudzony. Przypu-
śćmy, że jest nim atom oznaczony wskaźnikiem 1, a więc
|Ψ(0)i = |e

1

i ⊗ |g

2

i = (1/

√

2)(|si + |ai). Przyjmijmy też, jak

poprzednio, że odległość między atomami r

12

= λ/12, co

daje Γ

12

= 0,95 Γ oraz 2Ω

12

= 9,30 Γ. Ewolucję zgodności

C(t) dla takiego przypadku ilustruje rys. 6. Ponieważ stan
początkowy jest stanem iloczynowym, to C(0) = 0 i splą-
tania nie ma. Ale taki stan jest superpozycją stanów |si
oraz |ai, a co więcej, przy takim warunku początkowym
istnieją niezerowe koherencje, tzn. niezerowe są niediago-
nalne elementy macierzowe między stanami |si oraz |ai.
Powoduje to, że w ewolucji zgodności pojawiają się oscy-
lacje o częstości 2Ω

12

. Jak widać na rys. 6, w układzie

może pojawić się znaczny stopień splątania, C > 0,8, ob-
serwowany w pierwszym maksimum, chociaż na początku
splątania nie było. Oznacza to, że emisja spontaniczna nie
zawsze psuje korelacje kwantowe, ale może też w pewnych
sytuacjach takie korelacje kwantowe tworzyć.

Oscylacje widoczne na rys. 6 po pewnym czasie

(Γt ≈ 2) zanikają. Można je zaobserwować tylko w przy-
padku, gdy Ω

12

Γ. Na rysunku 6 uwidocznione zo-

stały także krzywe obrazujące sumę ρ

aa

(t) + ρ

ss

(t) i róż-

nicę ρ

aa

(t) − ρ

ss

(t) obsadzeń stanów antysymetrycznego

i symetrycznego. Widać wyraźnie, że stanowią one ob-
wiednie dla oscylacji C(t). Ten fakt ma prostą interpreta-
cję fizyczną w świetle tego, co powiedzieliśmy wcześniej
na temat ewolucji stanów antysymetrycznego i symetrycz-
nego. Otóż początkowo obsadzenia stanów |ai oraz |si
są jednakowe, ale stan |si zanika znacznie szybciej niż
stan |ai, a to oznacza, że po pewnym czasie (Γt ≈ 2) po-
pulacja stanu symetrycznego jest już prawie równa zeru,
podczas gdy populacja stanu antysymetrycznego jest cią-
gle niezerowa. Nadal mamy więc w układzie pewien sto-

pień splątania, który mierzony wartością zgodności C jest
równy populacji stanu antysymetrycznego. Dla dostatecz-
nie długich czasów C(t) = ρ

aa

(t), a więc to stan antysyme-

tryczny odgrywa kluczową rolę.

0

0,2

0,4

0,6

0,8

1

0

0,5

1

1,5

2

2,5

3

3,5

4

st

o

p

ie

ń

sp

lą

ta

n

ia

Γt

C

(t)

ρ

aa

+ ρ

ss

ρ

aa

− ρ

ss

Rys. 6. Ewolucja C(t); jeden atom wzbudzony (|Ψ(0)i =

|e

1

i ⊗ |g

2

i) przy r

12

= λ/12 (Γ

12

= 0,95 Γ, 2Ω

12

= 9,30 Γ)

Jak widać, znajomość stanów kolektywnych dwóch

atomów i ich ewolucji pozwala wejrzeć głębiej w fizyczną
naturę splątania kwantowego, a proste relacje między róż-
nymi stopniami splątania i fizycznymi parametrami opisu-
jącymi kolektywną emisję spontaniczną z układu dwóch
atomów mogą być bardzo pouczające.

Literatura

[1] A. Einstein, B. Podolsky, N. Rosen, Phys. Rev. 47, 777

(1935).

[2] Z. Ficek, R. Tanaś, Phys. Rep. 372, 369 (2002).
[3] R. Tanaś, Z. Ficek, J. Opt. B 6, S90 (2004).
[4] W.K. Wootters, Phys. Rev. Lett. 80, 2245 (1998).
[5] A. Peres, Phys. Rev. Lett. 77, 1413 (1996).
[6] M. Horodecki, P. Horodecki, R. Horodecki, Phys. Lett.

A223, 1 (1996).

Prof. RYSZARD TANAŚ jest fizykiem teoretykiem zajmującym się
optyką kwantową, a ostatnio także informatyką kwantową. Od
1993 roku kieruje Zakładem Optyki Nieliniowej IF UAM. W la-
tach 1999–2002 był członkiem Komitetu Fizyki PAN, jest członkiem
Rady Naukowej Krajowego Laboratorium FAMO. Przez trzy kaden-
cje działał w Komisji Elektroniki Kwantowej IUPAP jako członek,
sekretarz, a następnie wiceprzewodniczący. Jest kierownikiem Stu-
diów Doktoranckich na Wydziale Fizyki UAM. Czas wolny chętnie
spędza na górskich wędrówkach lub na nartach.

POSTĘPY FIZYKI

TOM 57

ZESZYT 3

ROK 2006

107