2.3. Prawa Kirchhoffa

I prawo Kirchoffa: Suma natężeń
prądów dopływających do węzła
(rozgałęzienia) obwodu jest równa
zeru.

Prądom dopływającym przypisujemy
znak plus, odpływającym z węzła –
znak minus.

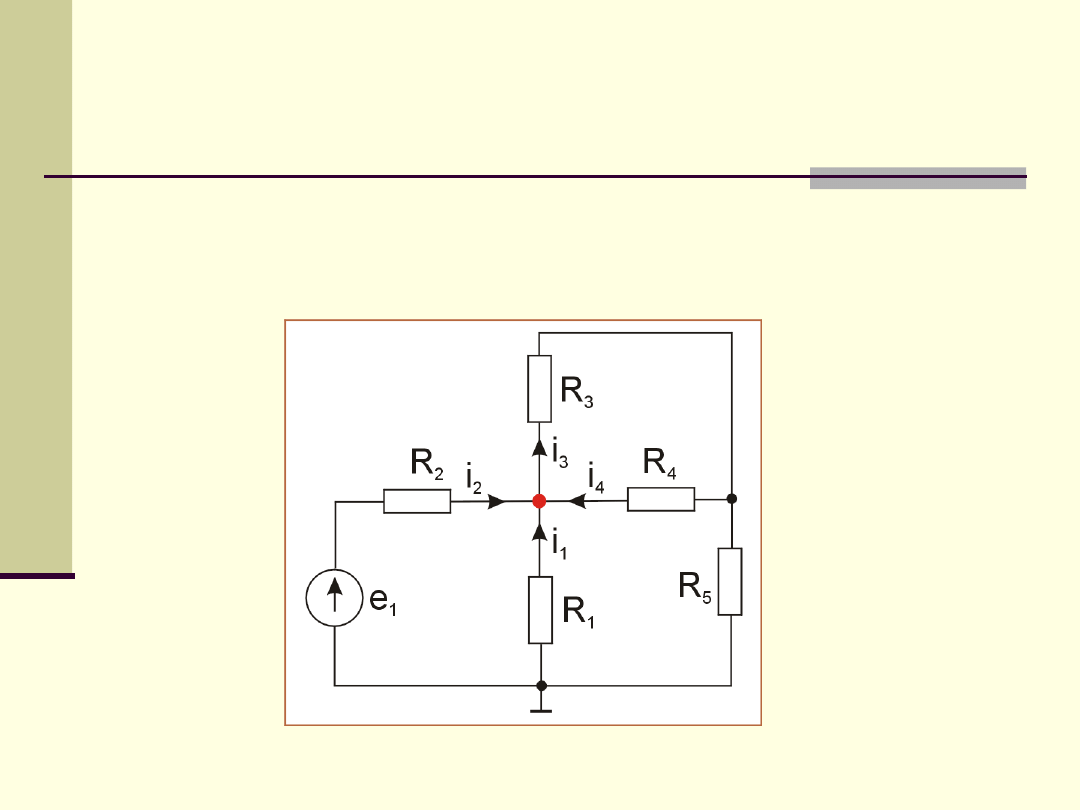
Przykład

)

8

(

0

4

3

2

1









i

i

i

i

2.3. Prawa Kirchhoffa

2.3. Prawa Kirchhoffa

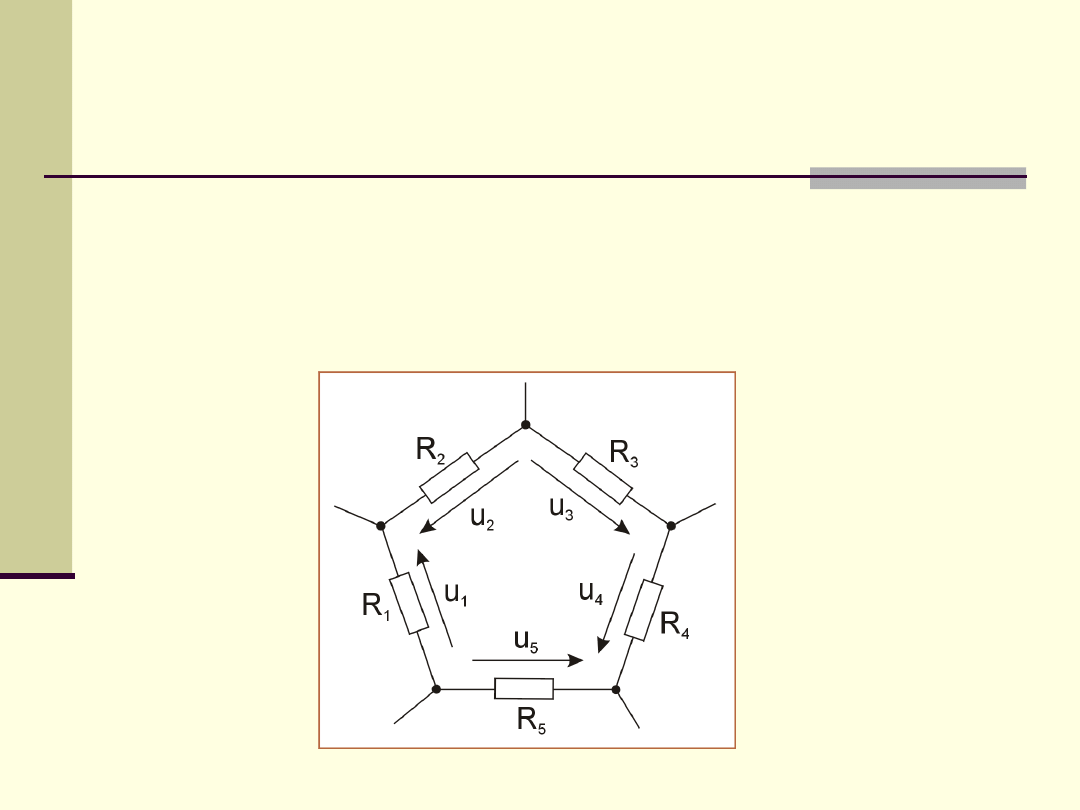
II prawo Kirchhoffa: Suma napięć na
poszczególnych

gałęziach

zamkniętego obwodu jest równa
zeru.

2.3. Prawa Kirchhoffa

Przykład

)

9

(

0

5

1







k

k

u

2.4. Elementy obwodów

elektrycznych

2.4.1. Klasyfikacje
Właściwości elektryczne elementów
są opisane przez związki (zależności
matematyczne) między prądami
i

napięciami

nazywane

charakterystykami elementu.

2.4. Elementy obwodów elektrycznych

Pojęcie

elementów

idealnych:

elementy

abstrakcyjne

o

uproszczonych chara-kterystykach,
które odzwierciedlają podstawowe
cechy danego typu elementów.

2.4. Elementy obwodów elektrycznych

Właściwości

rzeczywistych

elementów różnią się nieco od
właściwości elementów idealnych.
Klasyfikacja

elementów

elektronicznych (podobnie jak i
innych obiektów) może być oparta na
różnych kryteriach.

2.4. Elementy obwodów elektrycznych

Elementy możemy więc klasyfikować
według materiału z którego są
wykonane,

liczby

wyprowadzeń

zewnętrznych

(końcówek),

rozmiarów, budowy wewnętrznej itd.

2.4. Elementy obwodów elektrycznych

Z

punktu

widzenia

funkcji

spełnianych
w układach elektronicznych, istotne
są

następujące

podziały

(klasyfikacje):

2.4. Elementy obwodów elektrycznych



elementy liniowe lub nieliniowe;



elementy

inercyjne

lub

bezinercyjne;



elementy stratne lub bezstratne;



elementy czynne (aktywne) lub

bierne

(pasywne).

2.4. Elementy obwodów elektrycznych

Element nazywamy liniowym jeśli
jego podstawowa charakterystyka
jest wyrażona zależnością liniową
(spełnia zasadę superpozycji). W
przeciwnym

razie

element

jest

nieliniowy.

2.4. Elementy obwodów elektrycznych

Element

opisany

zależnością

prądowo-napięciową i = f(u) jest
bezinercyjny jeśli natężenie prądu w
chwili t zależy jedynie od napięcia w
tej samej chwili, a nie zależy od
wartości napięcia w przeszłości.

2.4. Elementy obwodów elektrycznych

Element jest inercyjny, jeśli aktualna
wartość natężenia prądu zależy od
wartości napięcia w przeszłości.
Analogiczne określenia odnoszą się
do elementu opisanego zależnością
napięciowo-prądową.

2.4. Elementy obwodów elektrycznych

Element jest bezstratny jeśli dopro-
wadzona

do

niego

energia

elektryczna jest w nim gromadzona i
może zostać odzyskana w całości w
formie elektrycznej.

2.4. Elementy obwodów elektrycznych

W elementach stratnych, część lub
całość

dostarczonej

energii

elektrycznej zostaje zamieniona na
ciepło i nie może być odzyskana w
formie energii elektrycznej.

2.4. Elementy obwodów elektrycznych

Elementy aktywne są zdolne do
wzmacniania

sygnałów

elektrycznych.

Moc

sygnału

elektrycznego

odbierana

z elementu aktywnego jest większa
od mocy sygnału doprowadzanego.

2.4. Elementy obwodów elektrycznych

To

wzmocnienie

mocy

sygnału

odbywa

się

na

koszt

mocy

składowych stałych prądów i napięć
doprowadzanych

do

elementu.

Elementy bierne nie są zdolne do
wzmacniania sygnałów.

2.4. Elementy obwodów elektrycznych

W następnym punkcie omawiamy
elementy bierne. Rolę elementów
czynnych (aktywnych) odgrywają
elementy

półprzewodnikowe

omawiane później.

2.4. Elementy obwodów elektrycznych

2.4.2. Podstawowe elementy bierne.
Podstawowe

elementy

bierne

używane w elektronice: oporniki,
kondensatory i cewki indukcyjne.
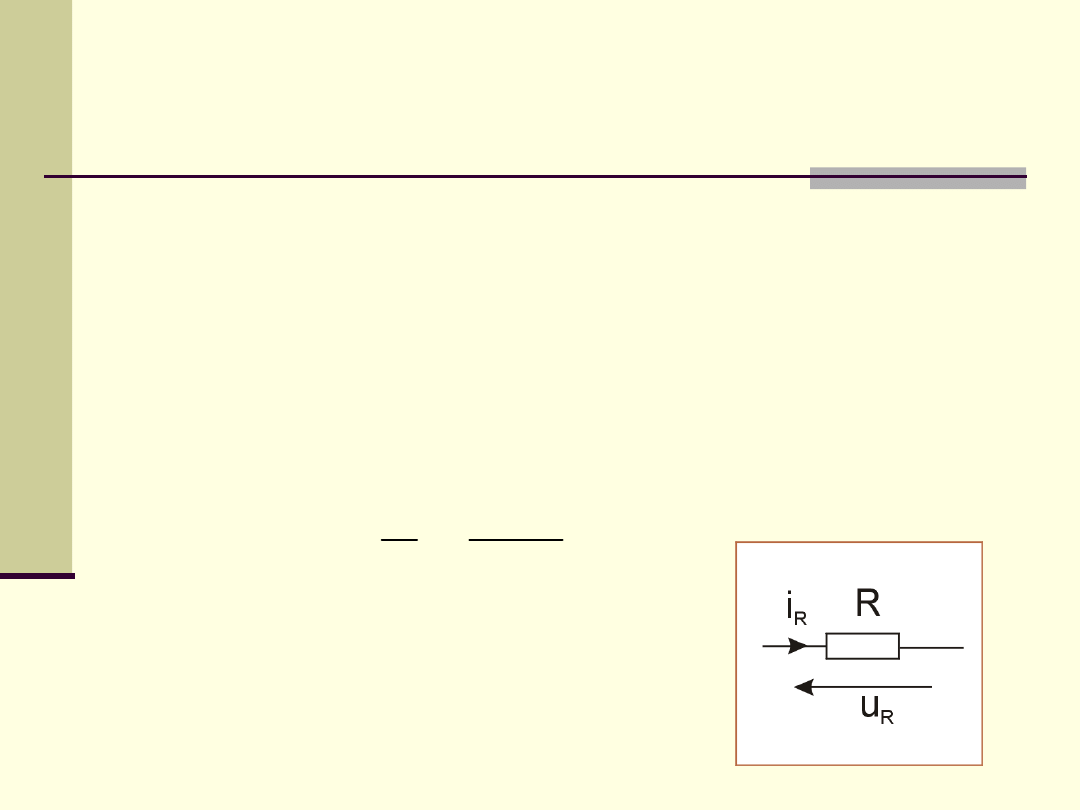
Idealny,

liniowy

element

rezystancyjny (opornik) jest opisany
prawem Ohma:

)

10

(

R

R

i

R

u





2.4. Elementy obwodów elektrycznych

Parametr R to oporność (rezystancja)
opornika. Rezystancja opornika o
długości l i powierzchni przekroju
poprzecznego S wynosi:

)

11

(

S

l

S

l

R













2.4. Elementy obwodów elektrycznych

 - oporność właściwa (rezystywność),


-

przewodność

właściwa

(konduktywność) materiału opornika.
Opornik

może

być

elementem

nieliniowym,

opisanym

przez

zależność:

lub:

)

12

(

)

(

R

R

R

i

f

u 

)

13

(

)

(

R

G

R

u

f

i 

2.4. Elementy obwodów elektrycznych

Typowe oporniki są wykonywane tak,
aby ich charakterystyka była bliska
zależności liniowej. Odchylenie od
liniowości

jest

traktowane

jako

nieidealność.

2.4. Elementy obwodów elektrycznych

Specjalne oporniki nieliniowe: np.
warystor. W tym przypadku, pomimo
nieliniowości,

element

jest

traktowany jako idealny.

2.4. Elementy obwodów elektrycznych

Idealny opornik jest elementem
stratnym i bezinercyjnym. Energia
elektryczna

doprowadzana

do

opornika w związku z wydzielaniem
mocy chwilowej:

)

14

(

R

R

R

i

u

p





2.4. Elementy obwodów elektrycznych

jest w nim w całości zamieniana na
ciepło. Wielkości u

R

, i

R

występujące w

opisach opornika oznaczają napięcie i
prąd w tej samej chwili t. Oznacza to,
że wartość napięcia na oporniku w
pewnej chwili t

0

nie zależy od

wartości prądu w przeszłości (dla t <
t

0

)

2.4. Elementy obwodów elektrycznych

W rzeczywistych opornikach, przy
szybkich

zmianach

prądów

lub

napięć,

obserwuje

się

efekty

inercyjne. Opornik rzeczywisty można
przedstawić

jako

połączenie

elementu idealnego z ele-mentami
pasożytniczymi,

pojemnościo-wymi

lub indukcyjnymi.

2.4. Elementy obwodów elektrycznych

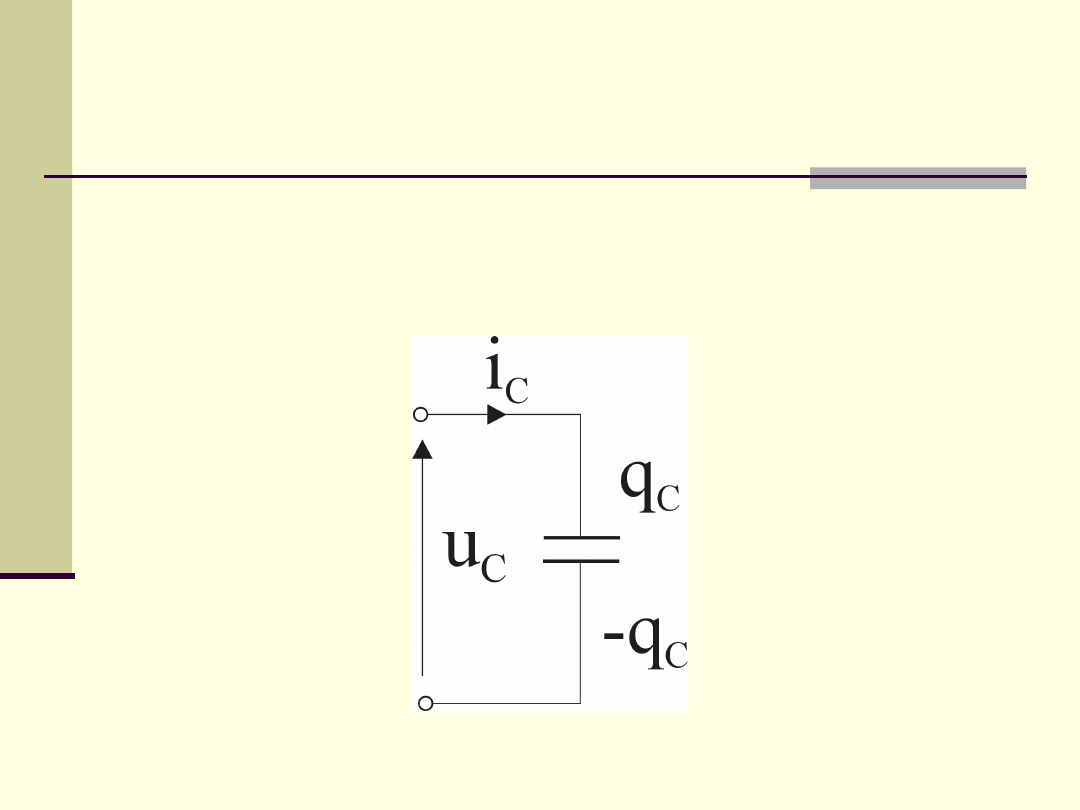
Idealny

element

pojemnościowy

(kondensator)

2.4. Elementy obwodów elektrycznych

Zależność definicyjna:

W przypadku liniowym:

Natężenie prądu:

 

C

C

C

u

f

q 

C

C

u

C

q





 

dt

du

u

C

dt

du

du

df

dt

dq

i

C

C

r

C

C

C

C

C











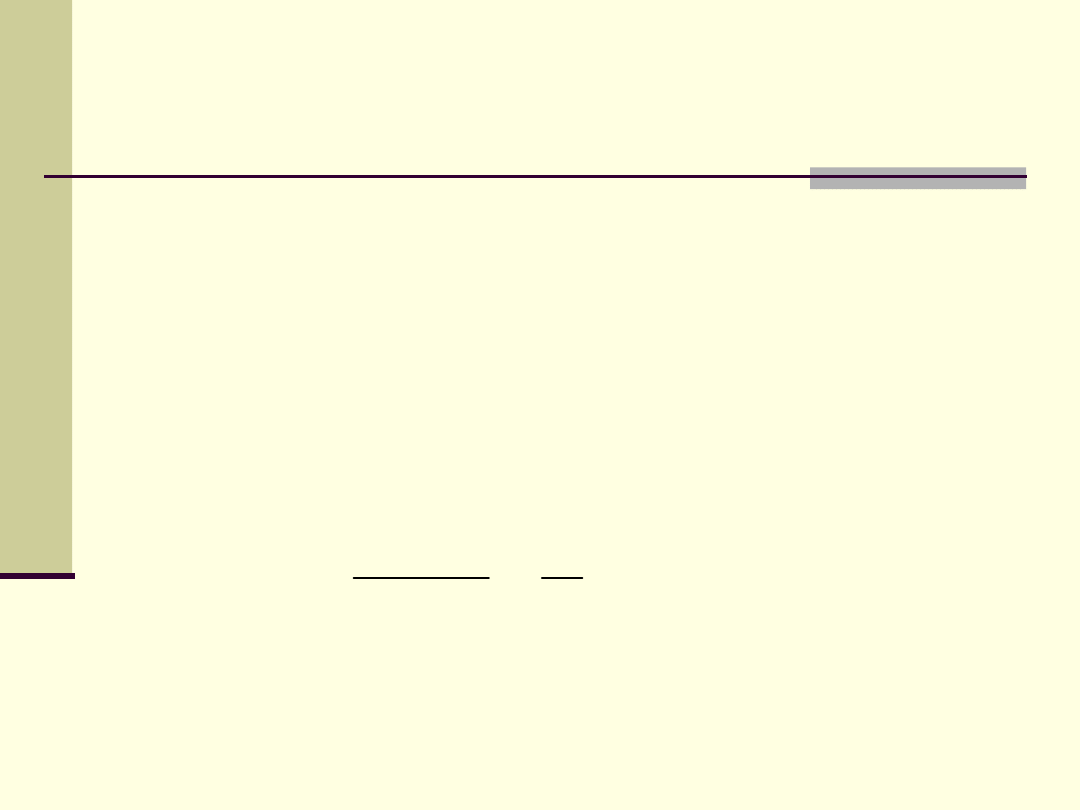
2.4. Elementy obwodów elektrycznych

W przypadku liniowym:

Napięcie w chwili t

0

:

.

)

(

const

C

u

C

C

r



















0

)

(

1

)

(

)

(

0

0

t

C

C

C

dt

t

i

C

C

t

q

t

u

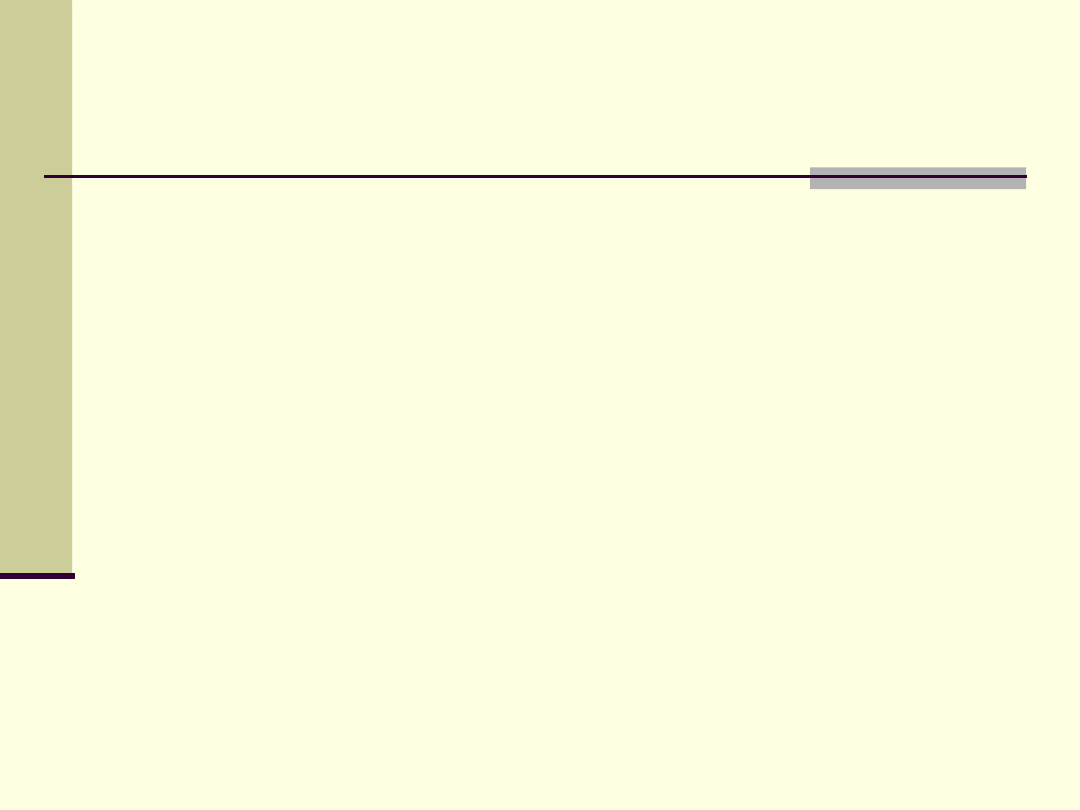
2.4. Elementy obwodów elektrycznych

Jeśli:

to:

t

U

t

u

cm

C



sin

)

(





t

U

C

t

i

cm

C





cos

)

(









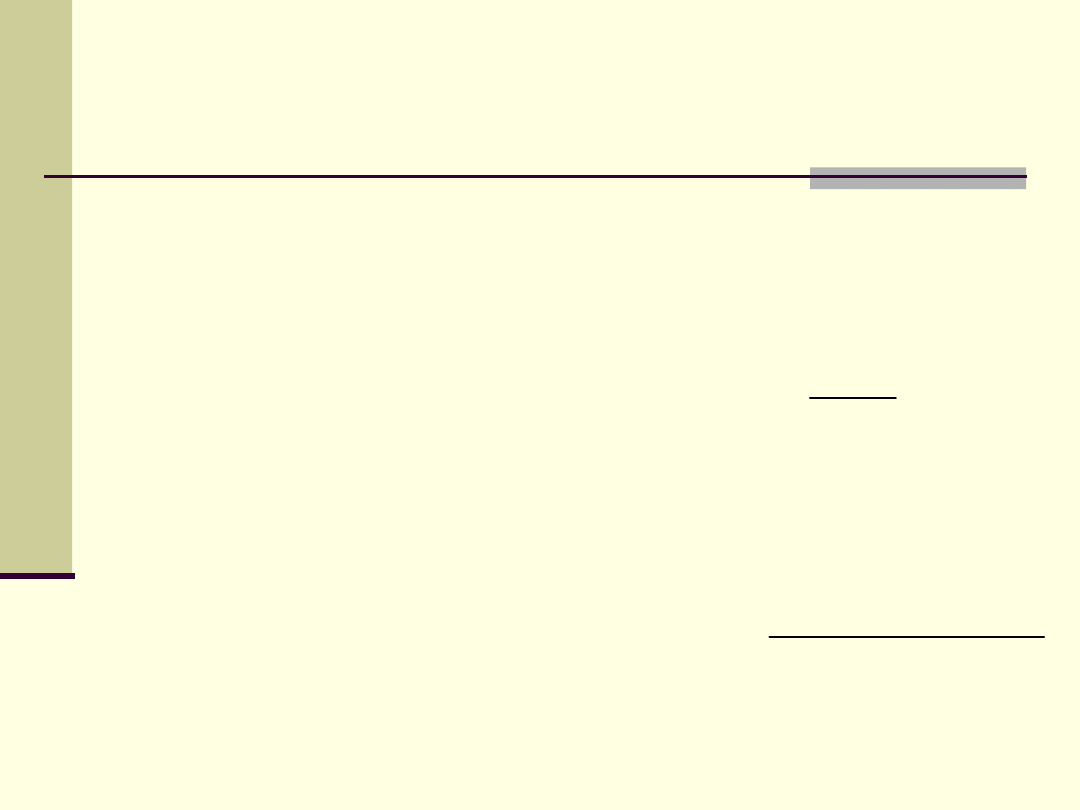
2.4. Elementy obwodów elektrycznych

Moc chwilowa doprowadzana do
idealnego kondensatora:

Energia dostarczona w przedziale
(t

1

,t

2

):

dt

du

u

C

t

u

t

i

t

p

C

C

C

C

C











)

(

)

(

)

(

















2

1

2

)

(

)

(

)

(

1

2

2

2

1

2

2

,

1

t

t

C

C

C

C

C

C

t

u

t

u

C

dt

t

p

W

W

W

2.4. Elementy obwodów elektrycznych

Gdzie:

Jeśli u

C

(t) okresowe, to zmiana energii

i moc średnia za pełny okres są
równe zeru.

2

)

(

)

(

2

t

u

C

t

W

C

C





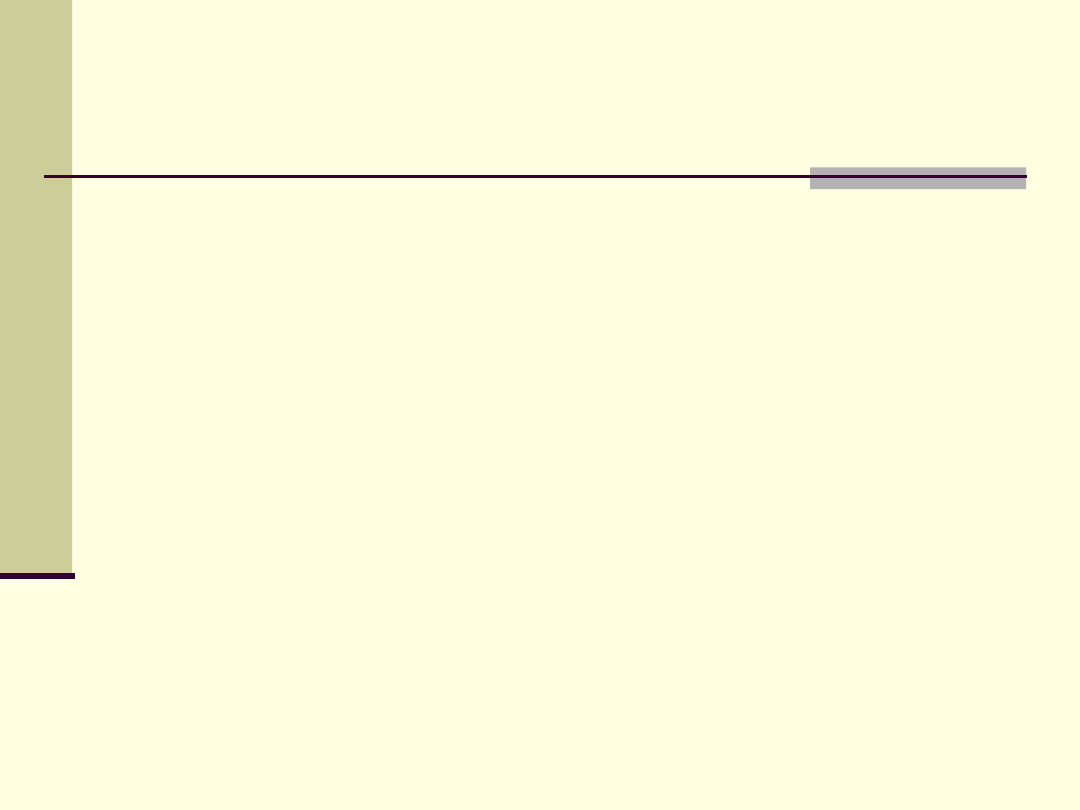
2.4. Elementy obwodów elektrycznych

Energia elektryczna zgromadzona
w idealnym kondensatorze może być
w pełni odzyskana.
Idealny kondensator jest elementem
bezstratnym, inercyjnym.

2.4. Elementy obwodów elektrycznych

Kondensator rzeczywisty.
Idealny element pojemnościowy –
przybliżenie. Lepsze przybliżenie, np.:

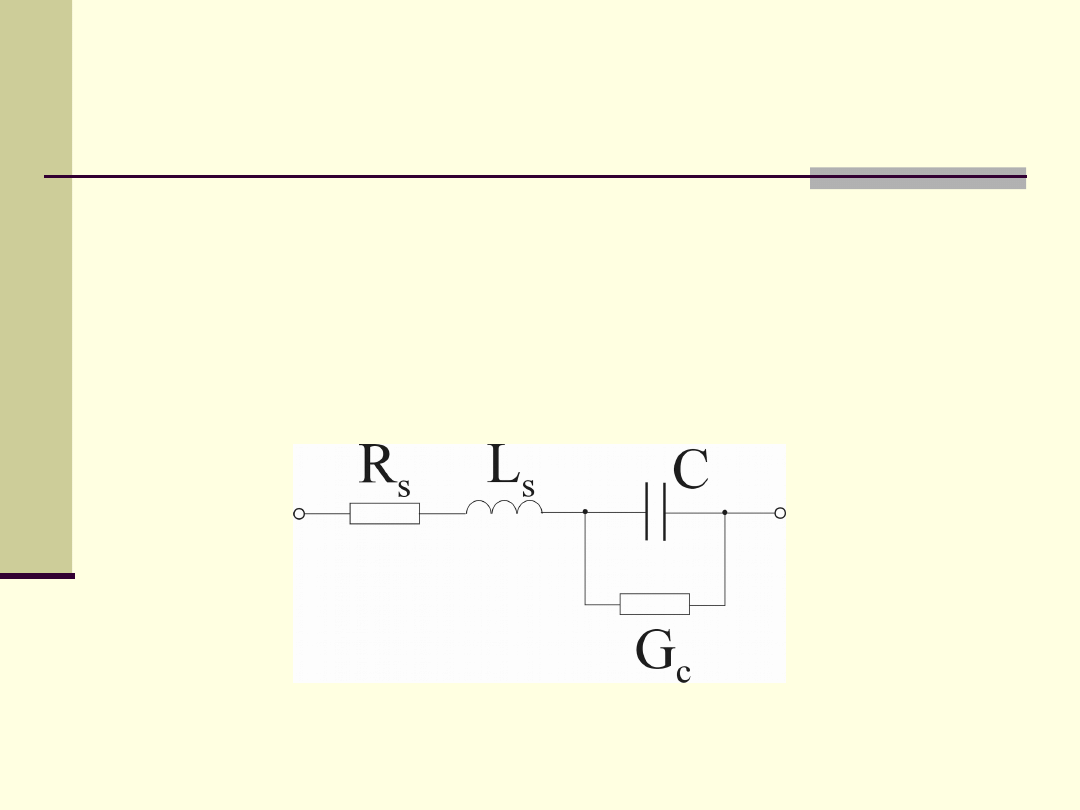
2.4. Elementy obwodów elektrycznych

Model rzeczywistego kondensatora.
C – idealny element pojemnościowy,
G

c

, R

s

), L

s

– elementy pasożytnicze. G

c

– możliwość przepływu prądu przy
u

C

= const.

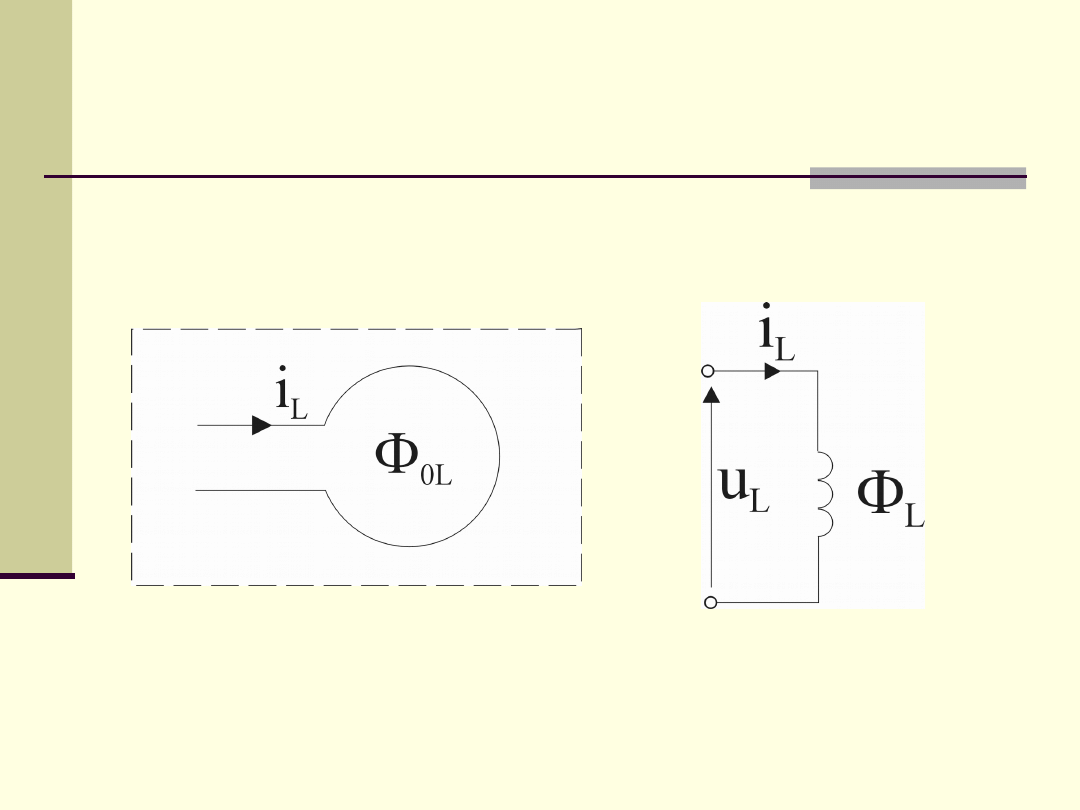
2.4. Elementy obwodów elektrycznych

Idealny element indukcyjny (cewka
indukcyjna).
Strumień magnetyczny (skojarzony)
zależy od natężenia prądu:

W przypadku liniowym:

L – indukcyjność cewki.

)

(

L

L

L

i

f





L

L

i

L





2.4. Elementy obwodów elektrycznych

2.4. Elementy obwodów elektrycznych

Napięcie na cewce (SEM samoindukcji)

W przypadku liniowym L

r

= const = L.

dt

di

i

L

dt

di

di

df

dt

d

u

L

L

r

L

L

L

L

L













)

(

2.4. Elementy obwodów elektrycznych

Prąd w chwili t

0

:

Cewka jest elementem inercyjnym.

Jeśli

to

















0

)

(

1

)

(

)

(

0

0

t

L

L

L

dt

t

u

L

L

t

t

i

t

I

t

i

m

L



sin

)

(





t

I

L

u

m

L





cos









2.4. Elementy obwodów elektrycznych

Doprowadzenie mocy do cewki 
gromadzenie

energii

pola

magnetycznego.

Energia

zgromadzona w cewce:

2

)

(

)

(

2

t

i

L

t

W

L

L





2.4. Elementy obwodów elektrycznych

Jeśli i

L

(t) okresowe, to zmiana energii

i moc średnia za okres są równe zeru.
Energia

może

zostać

w

pełni

odzyskana – idealna cewka jest
bezstratna.

2.4. Elementy obwodów elektrycznych

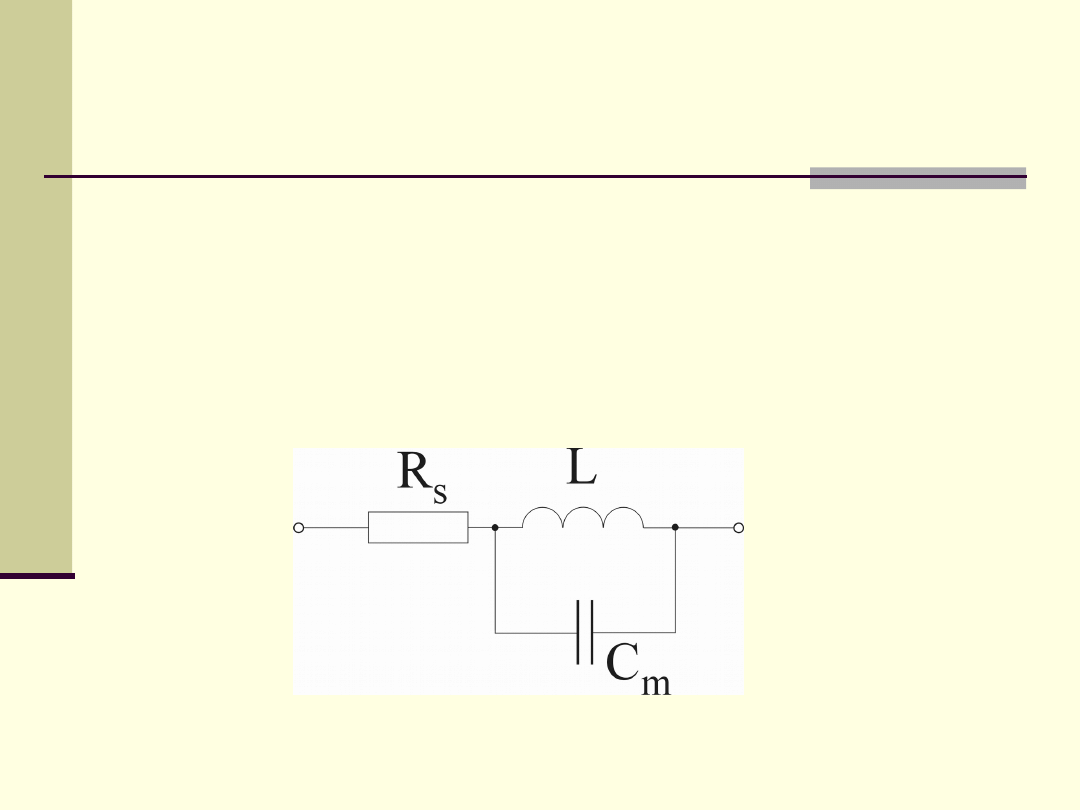
Rzeczywista cewka indukcyjna
Efekty

pasożytnicze:

rezystancja

uzwojeń

R

s

,

pojemności

międzyzwojowe - C

m

.

Model:

2.4. Elementy obwodów elektrycznych

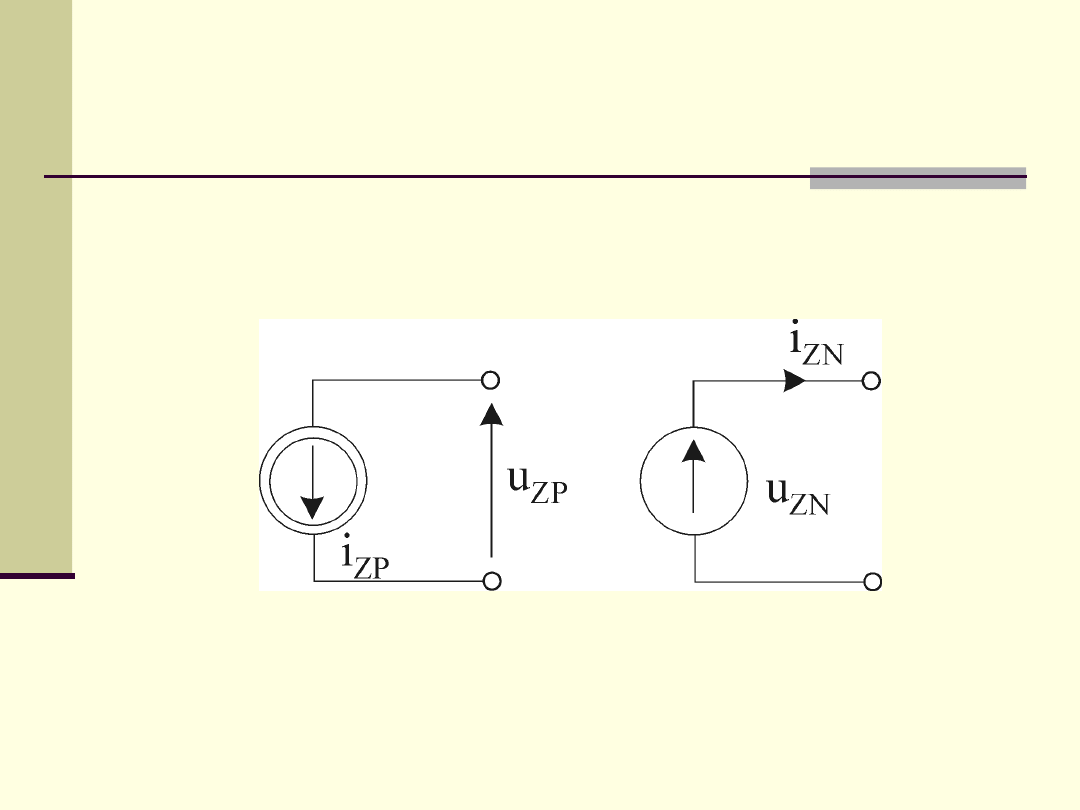
2.4.3.Elementy aktywne: Źródła

Niezależne źródło prądowe (NZP):

natężenie prądu i

ZP

o zadanym z góry

przebiegu

czasowym,

niezależne

od

napięcia u

ZP

Niezależne źródło napięciowe (NZN):
napięcie na końcówkach u

ZN

o założonym z

góry przebiegu czasowym, niezależne od
prądu i

ZN

2.4. Elementy obwodów elektrycznych

2.4. Elementy obwodów elektrycznych

Szczególny przypadek NZP lub NZN –
źródła prądu lub napięcia stałego.
Rezystancja,

pojemność,

indukcyjność dla R, C, L = const., to
elementy liniowe (spełniają zasadę
superpozycji).

NZP

i

NZN

nie

spełniają

zasady

superpozycji.

2.4. Elementy obwodów elektrycznych

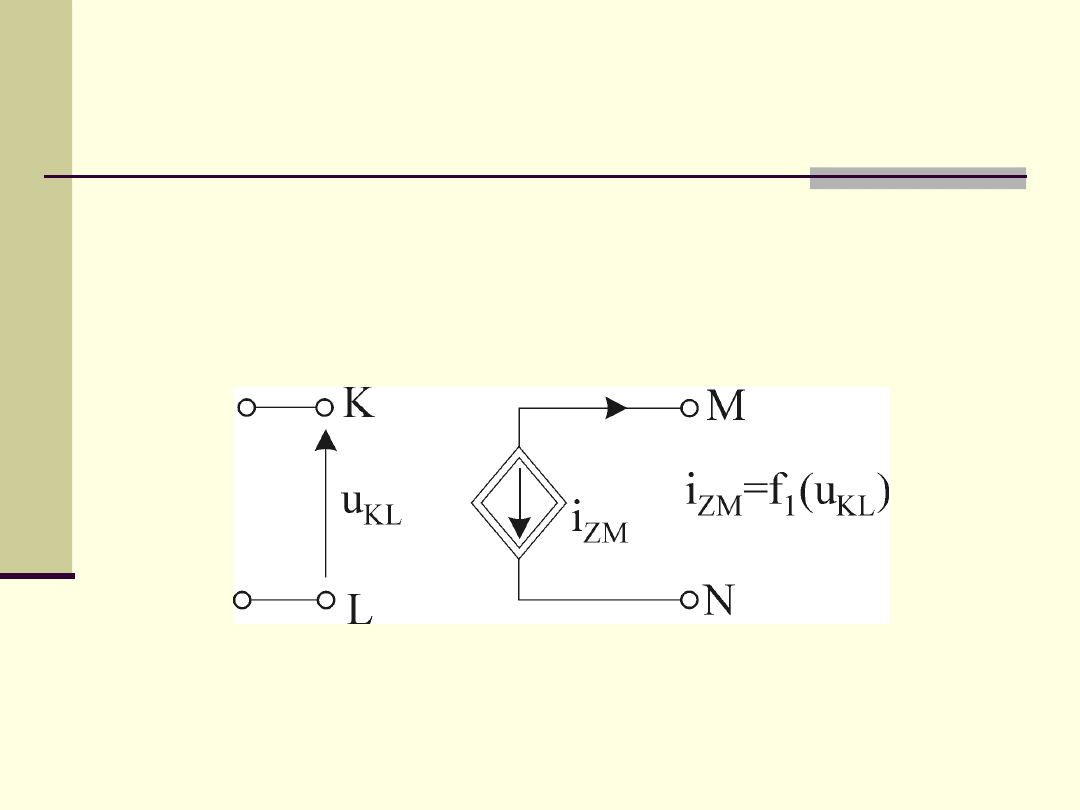
Źródło

prądowe

sterowane

napięciem

(ZPSN)

2.4. Elementy obwodów elektrycznych

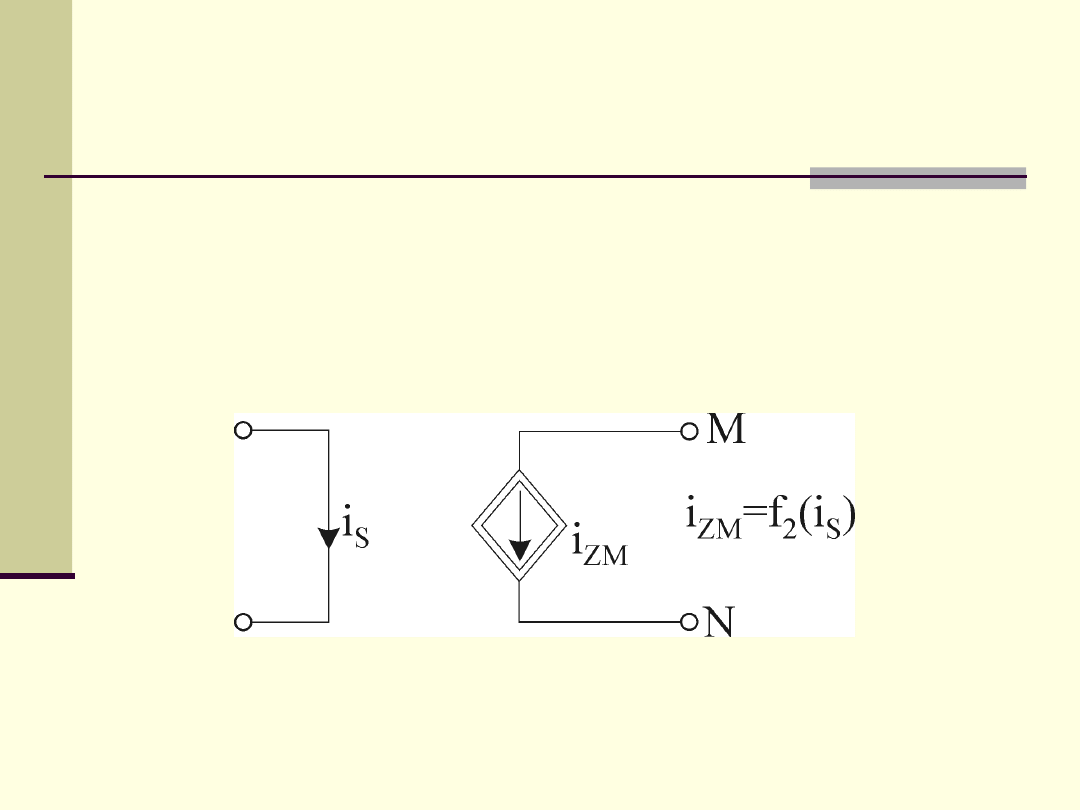
Źródło prądowe sterowane prądem

(ZPSP)

2.4. Elementy obwodów elektrycznych

Źródło

napięciowe

sterowane

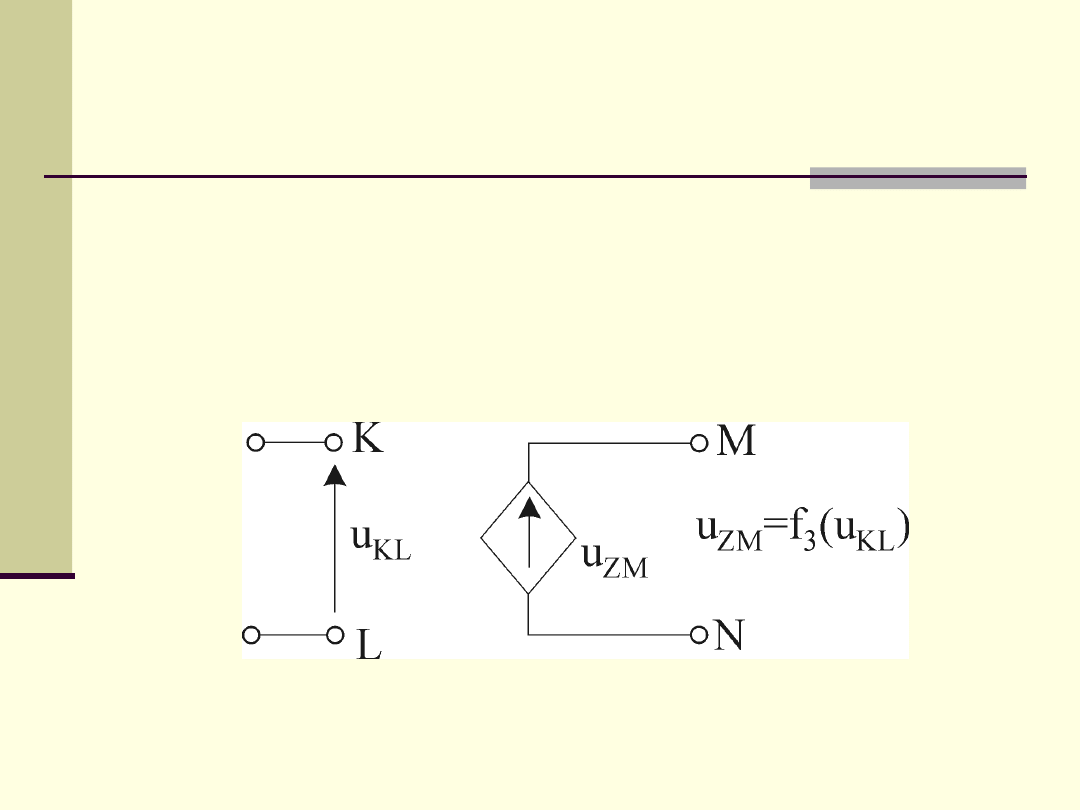
napięciem (ZNSN)

2.4. Elementy obwodów elektrycznych

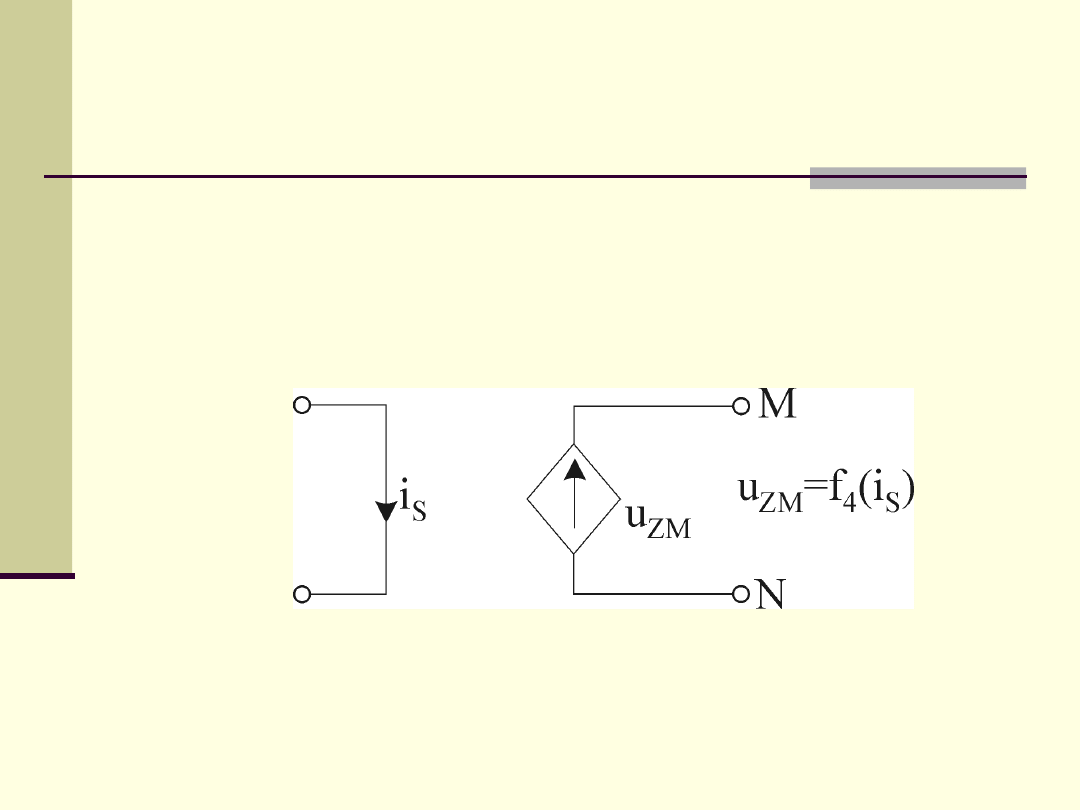
Źródło napięciowe sterowane prądem

(ZNSP)

2.4. Elementy obwodów elektrycznych

i

ZM



f(u

MN

) u

ZM



f(i

MN

)

Funkcje f

1

– f

4

w ogólności nieliniowe.

Szczególne przypadki: źródła liniowe.
LZPSN: i

ZM

= g

m

·u

KL

LZPSP: i

ZM

= K

i

·i

S

LZNSN: u

ZM

= K

u

·u

KL

LZNSP: u

ZM

= r

m

·i

S