PROGNOZOWANIE I SYMULACJE

Marcin Idzik

Szkoła Główna Gospodarstwa Wiejskiego

Wydział Ekonomiczno - Rolniczy

Katedra Ekonomiki Rolnictwa

i Międzynarodowych Stosunków Gospodarczych

Warszawa, 2006 r.

METODY PROGNOZOWANIA

SZEREGÓW CZASOWYCH

Szereg czasowy



Jednowymiarowy szereg czasowy (pokazuje stany zmiennej

prognozowanej y w momencie lub okresie t, gdzie: t =

1,2,3...,n)

]

,...,

,

,

[

3

2

1

n

y

y

y

y

y 

2004

Q1

Q2

Q3

Q4

Liczba pracujących
w tys. osób

14319

14518

14727

14540

Tabela 1. L.pracujących w roku 2004 w Polsce (stan w końcu kwartału)

MODELE

PRZYCZYNOWO-

SKUTKOWE

PROGNOZOWANIE

NA PODSTAWIE

SZEREGÓW

CZASOWYCH

METODY

HEURYSTYCZNE

METODY

ANALOGOWE

METODA

Czy można przewidywać przyszłość

spoglądając w przeszłość?

„To co

było

, jest tym, co

będzie

,

A to, co się

stało

,jest tym,

co znowu się

stanie

”

Koh.

Co będzie?

wystąpiło w przeszłości

wskazuje na to częstość występowania

wskazuje na to silne powiązanie z innymi

zdarzeniami które wystąpiły

zdarzenie nastąpi ponieważ:

Analiza szeregów

czasowych

Identyfikacja

struktury,

charakterystyka

przebiegu

SKŁADNIKI ZMIENNOŚCI - POMIAR

1000

1500

2000

2500

3000

3500

4000

4500

5000

st

y

-9

1

st

y

-9

2

st

y

-9

3

st

y

-9

4

st

y

-9

5

st

y

-9

6

st

y

-9

7

st

y

-9

8

st

y

-9

9

st

y

-0

0

0

1

-s

ty

0

2

-s

ty

0

3

-s

ty

0

4

-s

ty

0

5

-s

ty

ty

s.

s

z

t

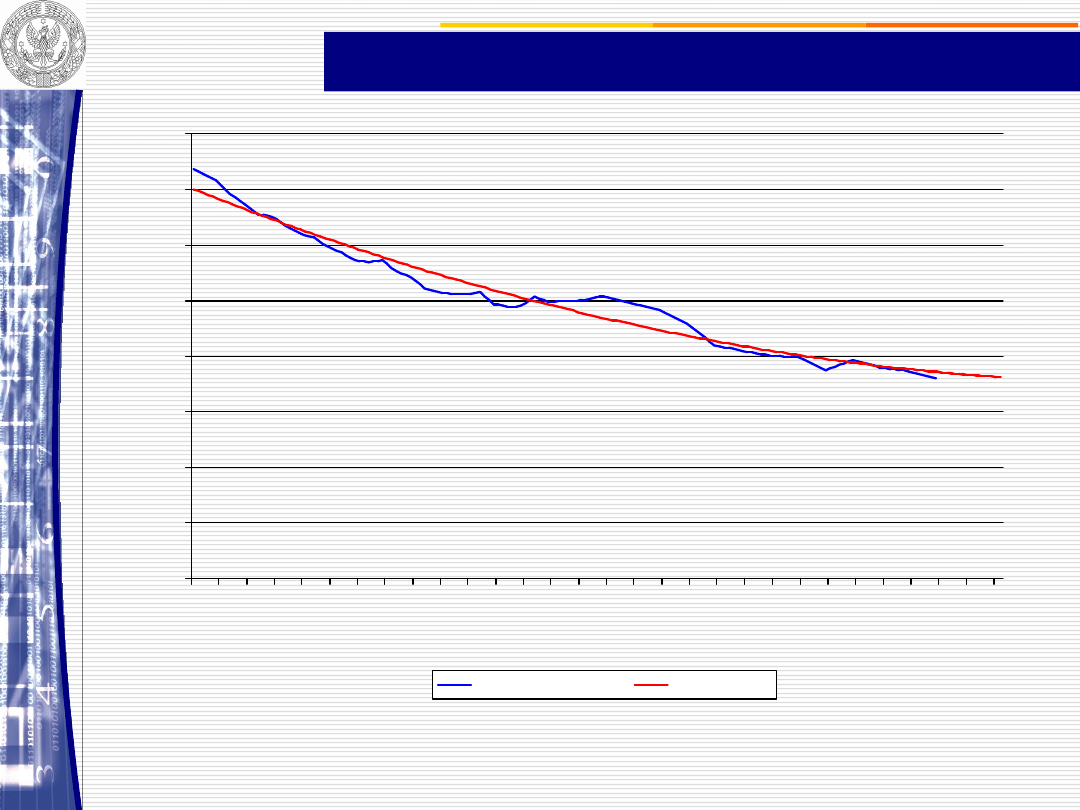
Pogłowie krów

Prognoza

PROGNOZA ORAZ POGŁOWIE KRÓW W POLSCE

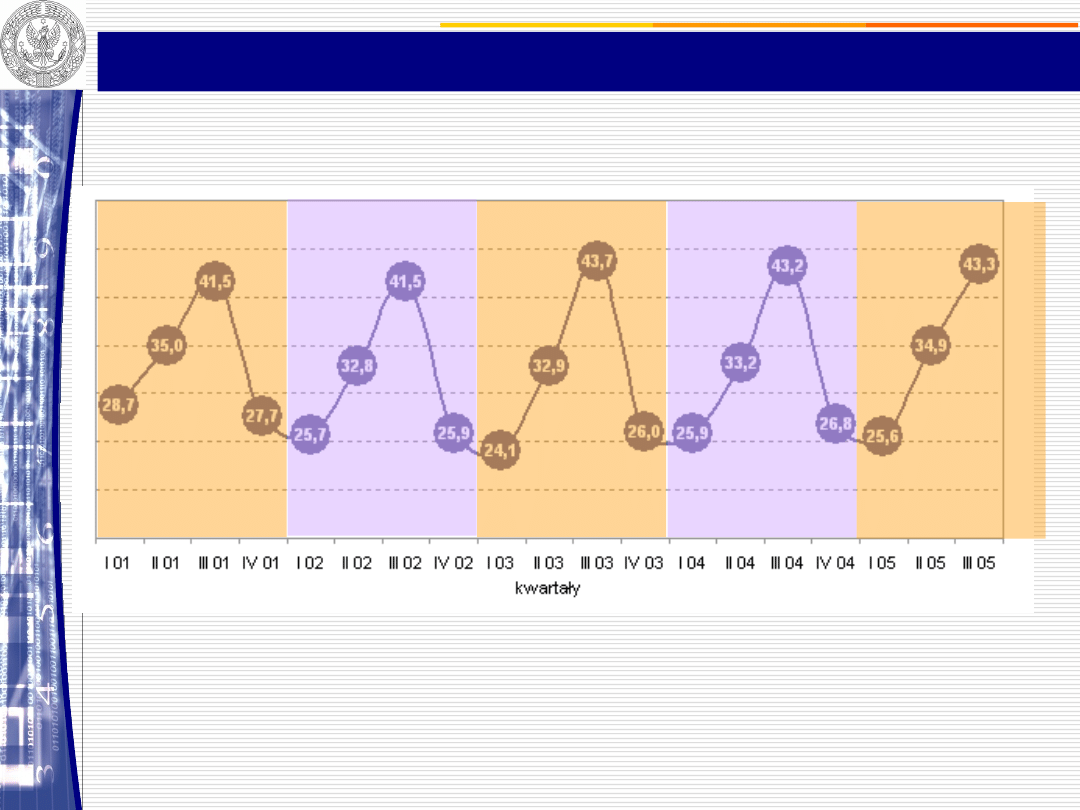
Wykorzystanie miejsc

noclegowych w latach 2001-2005 (%)

01/9
9

01/9
3

05/9
5

01/0
3

06/9
4

11/9
7

10/0
1

10/0
4

Y

t

-S

t

=T

t

+C

t

+S

t

+I

t

-S

t

=T

t

+C

t

+I

t

05/0
4

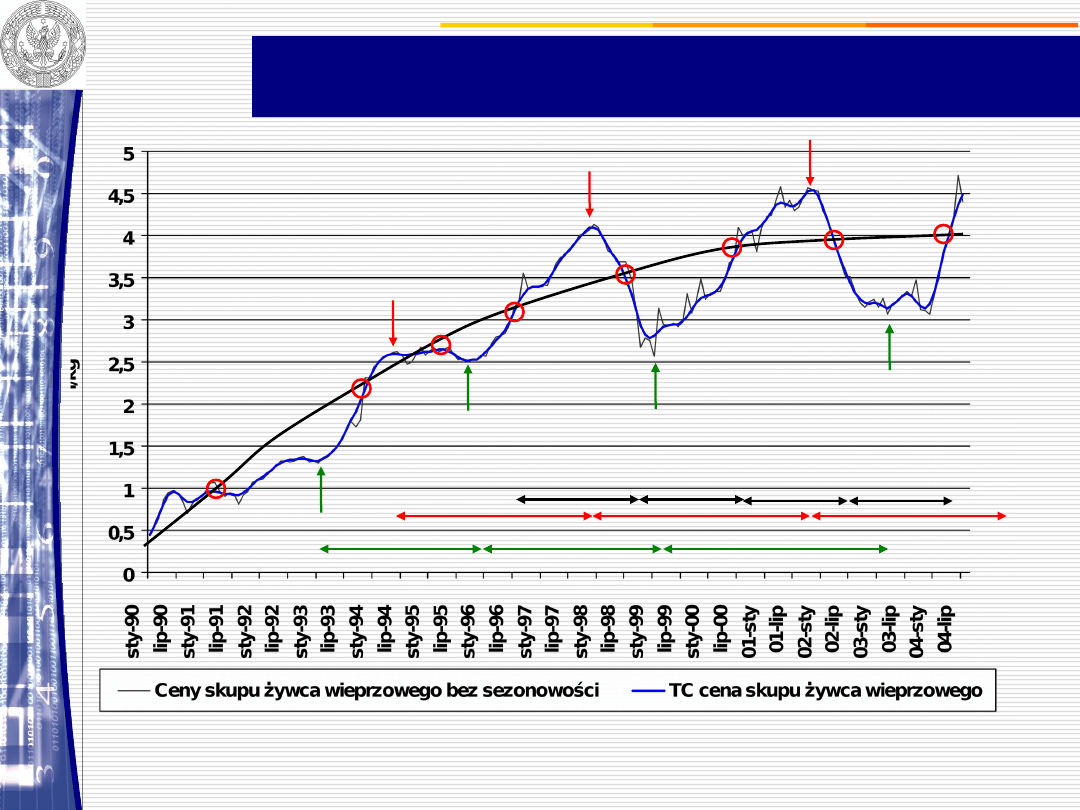
CENY SKUPU ŻYWCA WIEPRZOWEGO W POLSCE -

cechy morfologiczne cyklu

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

Modele szeregów czasowych

warto stasować

gdy:

•

trudno jest przedstawić ilościowo współzależności;

•

odpowiedź co będzie, a nie dlaczego;

•

niewiele zmiennych objaśniających;

•

redukcja kosztów;

Modele szeregów czasowych

ograniczenia:

•

dysponowanie długimi szeregami czasowymi;

•

wg zasady status quo (niezmienność czynników

otoczenia), postawa pasywna;

•

zmiany wyłącznie o charakterze ilościowym;

•

niezbędna identyfikacja składników zmienności

szeregu czasowego.

METODY PROGNOZOWANIA

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Metody naiwne – najprostsze metody



Metoda oparta na błądzeniu
przypadkowym:

n

T

y

y 

wartość prognozy równa jest
ostatniej zaobserwowanej
wartości zmiennej
prognozowanej

t

y

t

y

T

q

t

2

1

48

-

-

2

51

48

9

3

49

51

4

4

50

49

1

5

48

50

4

6

x

48

18

%

3

,

4

100

5

,

49

12

,

2

*







V



Metoda dla szeregu
czasowego z trendem:





1









n

n

n

T

y

y

y

y

Przy obliczaniu prognozy
uwzględniamy ostatni
przyrost wartości zmiennej
prognozowanej

t

y

t

y

n

-y

n-1

y

T

q

t

2

1

48

-

-

-

2

51

3

-

-

3

49

-2

54

25

4

50

1

47

9

5

48

-2

51

9

6

x

x

46

43

%

73

,

7

100

49

79

,

3

*







V

Metody naiwne – najprostsze metody



Metoda dla zmiennej

wykazującej tendencję do

zmian o pewien procent –

prognozowanie w oparciu o

średnie tempo zmian:

n

T

n

T

i

y

y







t

y

t

y

T

1

48

0,0625

-

2

x

x

51

i

Metody naiwne – najprostsze metody



Metoda dla szeregu czasowego z
wahaniami sezonowymi

t

y

t

y

T

q

t

2

1

48

-

-

2

51

-

-

3

49

-

-

4

50

-

-

5

48

48

0

6

49

51

4

7

52

49

9

8

48

50

4

9

x

48

17

m

n

T

y

y







1

Prognozą jest poziom ostatniej
znanej realizacji badanej
zmiennej w okresie
jednoimiennym;
m - oznacza liczbę faz w cyklu

%

18

,

4

100

25

,

49

06

,

2

*







V

Metody naiwne – najprostsze metody

Podsumowanie metod naiwnych:



Metody naiwne są najprostszymi metodami prognozowania
krótkookresowego;



Wykorzystuje się je najczęściej do porównań trafności
prognoz zbudowanych na ich podstawie oraz na podstawie
bardziej złożonych metod

Składowe

szeregu

czasowego

Stały (przeciętny) poziom i wahania

przypadkowe

Przesłanki metody

Nie

nastąpią

zmiany

w

sposobie

oddziaływania czynników określających

zmienną

prognozowaną,

niewielkie

wahania przypadkowe

Postawa, zasada, reguły

prognostyczna

Postawa pasywna, zasada status quo,

reguła podstawowa prognozowania

Horyzont prognozy

Jeden okres (moment)

Ocena prognozy

Błędy ex post

Zalety metody

Prosty algorytm, łatwość zrozumienia,

szybkie i tanie prognozowanie

Wady metody

Niska jakość prognozy, ocena jedynie za

pomocą błędów ex post

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Metoda średniej ruchomej



Średnia ruchoma prosta:











n

k

n

t

t

T

y

k

y

1

1

Prognoza jest tu średnią arytmetyczną wartości zmiennej
prognozowanej z wybranego przedziału czasu (przedziału
wygładzania);
k – stała wygładzania (przyjmuje się tę, dla której wartość
średniego błędu ex-post prognoz wygasłych jest
najmniejsza)

Gdy zaobserwowany w okresie badawczym poziom wartości
zmiennej prognozowanej jest względnie stały, z pewnymi
niewielkimi odchyleniami przypadkowymi.

Średnia ruchoma

podstawowe wyróżniki:

prognozy krótkookresowe (max rozsądny horyzont =

1);

•

względnie stały poziom zjawiska wahania

przypadkowe;

•

wg zasady status quo, postawa pasywna;

•

nie nastąpią zmiany w sposobie oddziaływania

czynników określających zmienną prognozowaną, mogą

wystąpić duże wahania przypadkowe

•

prognozowanie oraz wygładzanie szeregów

czasowych;

•

konieczność doboru stałej k i współczynników

wagowych w (minimalizacja błędów),

Średnia ruchoma,

problem do rozwiązania:

•

wybór szerokości okna wygładzania l ;

•

kryterium wyboru szerokości okna

wygładzania;

»

minimalizacja błędu prognoz ex post;

»

ekspercka ocena.

Kryterium wyboru szerokości okna
wygładzania;

»

minimalizacja błędu prognoz ex

post;

¤

średni absolutny błąd prognozy,

¤

średni kwadrat błędu,

¤

odchylenie standardowe błędu prognozy

¤

średni absolutny błąd procentowy

Średnia ruchoma,

uwaga:

•

wysoka wartość stałej wygładzania:

»

silny efekt wygładzania;

»

prognoza determinowana starszą informacją;

»

zatarcie krótkookresowych zmian poziomu

zjawiska;

»

brak reakcji na zmiany poziomu zmiennej

prognozowanej;

»

intensywna eliminacja wpływu wahań

przypadkowych;



Średnia ruchoma
ważona:













n

k

n

t

t

t

T

w

y

y

1

Uwzględnia postulat
nadawania zróżnicowanego
znaczenia informacjom z
różnych okresów;
w

t

- waga













n

k

n

t

t

t

w

w

1

1

1

,

0

(

METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Modele ze

stałym poziomem

zmiennej prognozowanej:

Metoda naiwna;
Metoda średniej ruchomej prostej i ważonej;
Prosty model wygładzania wykładniczego;
Modele autoregresji i średniej ruchomej.

Modele z

tendencją rozwojową

zmiennej prognozowanej:

Analityczne modele trendu,
Model liniowy Holta, Browna II i III rzędu;
Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami sezonowymi

zmiennej prognozowanej:

Metoda wskaźników;
Model Wintersa;
Metoda trendów jednoimiennych okresów;.
Analiza harmoniczna;
Metoda L.R Kleina ze zmiennymi zero-jedynkowymi.

Modele z

wahaniami cyklicznymi

zmiennej

prognozowanej

Modele autoregresji i średniej ruchomej

ARMA i ARIMA

Ekstrapolacja trendu

warto stasować gdy:

•

trudno jest przedstawić ilościowo

współzależności;

•

odpowiedź co będzie, a nie dlaczego;

•

niewiele zmiennych objaśniających:

•

łatwo przewidzieć poziom zmiennej

objaśniającej dla badanego okresu;

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

Ekstrapolacja trendu

podstawowe wyróżniki:

•

prognoza ilościowa o charakterze ekstrapolacyjnym;

•

prognozy średniookresowe;

• zmienność szeregu determinowana jest przez trend,
wahania przypadkowe;

•

wg zasady status quo, postawa pasywna;

•

zgodnie z założeniami klasycznej teorii predykcji;

•

nie uwzględnia zmian kierunku trendu;

•

ryzyko oparcia prognozy na dobrym modelu, ale

nieaktualnym dla ostatnich obserwacji, ostre założenie o
niezmienności mechanizmu rozwojowego zjawisk.

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

Modele trendu



Modele uwzględniające składową systematyczną – trend

oraz składnik losowy przyjmują następującą postać:

 

 

t

t

t

t

u

t

f

y

u

t

f

y









Najczęściej wykorzystywana funkcja trendu:

•Liniowa

•Wykładnicza

•Potęgowa

UWAGA ! – w zależności od rozwoju zmiennej
prognozowanej można zaproponować wiele
innych postaci analitycznych

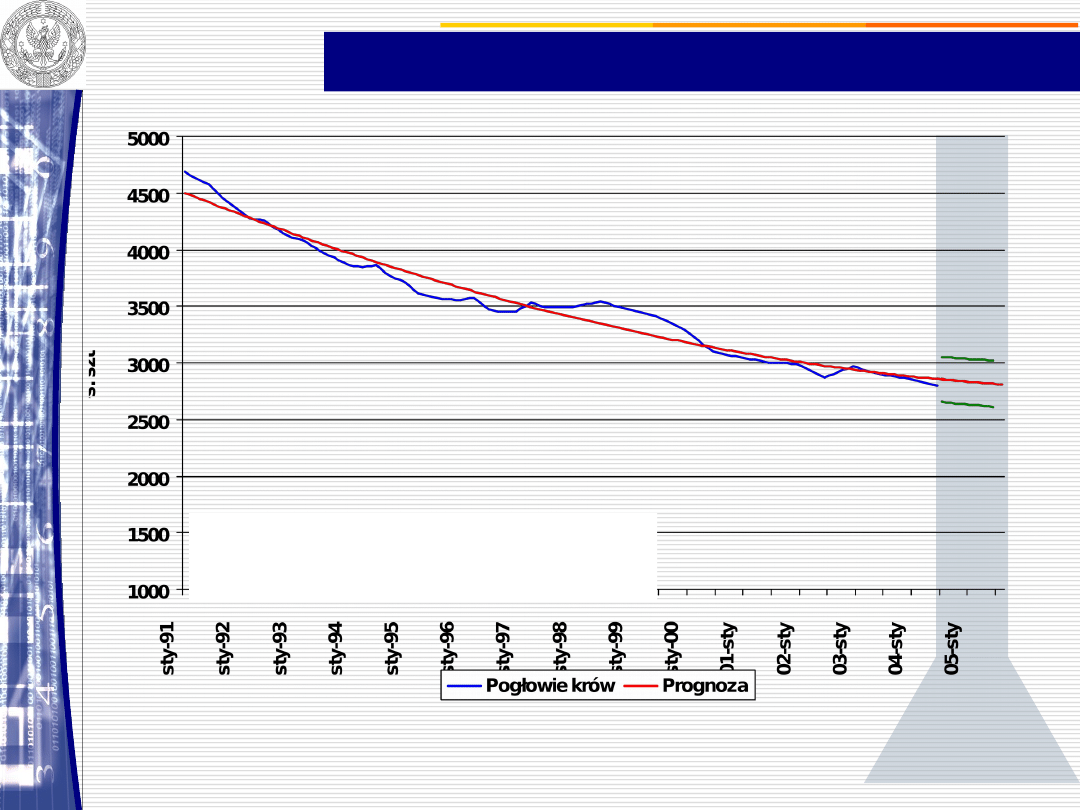
Horyzont

prognozy

Pogłowie krów= 4517,69-16,5656*t +
0,0390241*t^2

R

2

=0,96, RMSE=98, MAPE=2,2%

PROGNOZA ORAZ POGŁOWIE KRÓW W POLSCE

Ekstrapolacja trendu,

problem do

rozwiązania:

•

wybór funkcji trendu;

»

analiza graficzna;

»

metoda heurystyczna;

»

badanie przyrostów.

•

weryfikacja modelu;

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

Ekstrapolacja trendu,

weryfikacja modelu:

•

merytoryczna:

»

ocena parametrów;

»

zgodność z teorią i naszą wiedzą o

zjawisku;

•

statystyczna:

»

istotność parametrów strukturalnych

»

autokorelacja składników losowych

»

stacjonarność składników losowych

»

losowości składników losowych

»

normalności rozkładu odchyleń losowych

»

poprawności postaci analitycznej

»

heteroskedastyczność

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

KLASYCZNE MODELE TRENDU

Klasyczne założenia teorii predykcji

1.

Znajomość modelu kształtowania się zmiennej
prognozowanej



Znajomość postaci analitycznej występujących
zależności między zmiennymi modelu



Znajomość wartości ocen parametrów strukturalnych



Znajomość wartości ocen parametrów struktury
stochastycznej (wariancji resztowej, macierzy wariancji
i kowariancji ocen parametrów strukturalnych)

2.

Stabilność prawidłowości ekonomicznej w
czasie

.

Model powinien być dobrym odzwierciedleniem
badanych prawidłowości nie tylko w okresie, z
którego pochodzą dane do estymacji, lecz również
w okresie, na który się prognozuje



Stabilność postaci analitycznej modelu



Stabilność zbioru zmiennych objaśniających



Stabilność wartości parametrów strukturalnych

Klasyczne założenia teorii predykcji

3.

Stabilność rozkładu składnika losowego



Rozkład składnika losowego nie ulega zmianom w
czasie



Mały i stabilny błąd szacunku modelu (odchylenie
standardowe reszt) gwarantuje otrzymanie prognoz
obarczonych małym błędem systematycznym

Klasyczne założenia teorii predykcji

4.

Znajomość wartości zmiennych objaśniających
modelu w okresie prognozowanym



Plany, założenia



Prognozy zmiennych objaśniających na podstawie
tendencji rozwojowej lub na podstawie modeli
opisowych

Klasyczne założenia teorii predykcji

5.

Dopuszczalność ekstrapolacji modelu poza

zaobserwowany obszar zmienności

zmiennych objaśniających



Ma na celu zapobieżenie bezkrytycznym

uogólnieniom



Nie ma gwarancji budowy dobrych prognoz na

podstawie zaobserwowanego poziomu zmienności

zmiennych objaśniających w przeszłości

Klasyczne założenia teorii predykcji

UWAGA !

UWAGA !



W przypadku prognozowania krótkookresowego

przyjmuje się, że założenia klasyczne są spełnione



Wnioskowanie na dłuższe okresy wymaga jednak

modyfikacji założeń ze względu na niestałość

struktury ekonomicznej i możliwość zmian

parametrów modeli w czasie

Zmodyfikowane założenia teorii predykcji

1.

Znajomość modelu kształtowania się zmiennej prognozowanej,

który odzwierciedla prawidłowość rozwoju tej zmiennej także w

przypadku prawie stabilności tej prawidłowości (zmiany

powolne, stabilne, mierzalne)

2.

Stabilność lub prawie stabilność prawidłowości ekonomicznej w

czasie

3.

Stabilność lub prawie stabilność rozkładu składnika losowego

modelu

4.

Znajomość wartości zmiennych objaśniających modelu lub ich

rozkładu prawdopodobieństw w okresie prognozowanym

5.

Możliwość ekstrapolacji modelu poza obszar zmienności z

błędem nie większym od zadanego

Rola składnika losowego w procesie predykcji



Jeśli przyjmiemy model ekonometryczny postaci:

u

Xb

y





Składnik losowy = różnica między rzeczywistą
wartością zmiennej objaśnianej, a jej wartością
teoretyczną:

Xb

y

u





Wpływ składników losowych na proces predykcji:

 wywołanie odchyleń wartości zmiennej prognozowanej
od prognozy

 średnie błędy szacunku parametrów strukturalnych
modelu zależą od wariancji składników losowych

Wpływ składników losowych na proces predykcji
jest tym większy im większa jest ich wariancja

Duża wariancja składników losowych = brak możliwości
oszacowania modelu z wystarczającą do celów
prognostycznych dokładnością. Nie możliwe jest też
zbudowanie dokładnych prognoz.

Wzrost wariancja składników losowych w czasie = dokładność
wnioskowania w przyszłość maleje.

Wzrost wariancji składników losowych w czasie wyraźny i
trwały = bram możliwości wykorzystania do celów
prognostycznych zbudowanego modelu

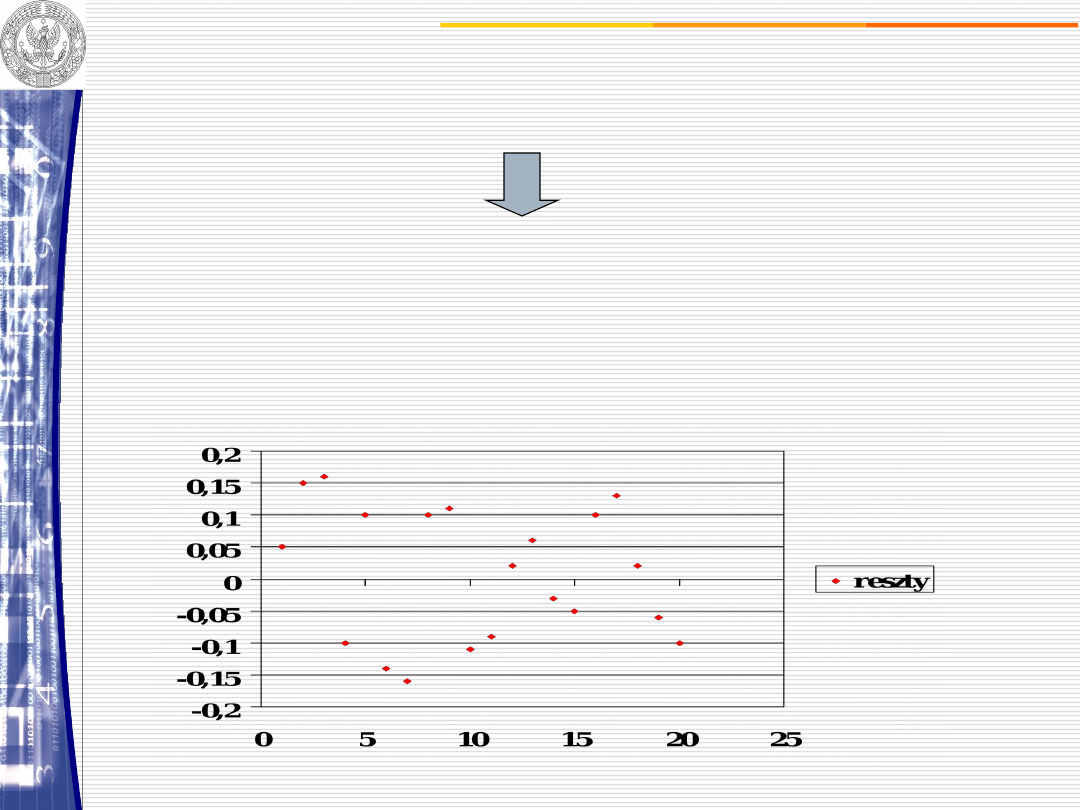
UWAGA: składnik losowy nie jest bezpośrednio obserwowalny

Możemy otrzymać oceny jego wartości poprzez obliczenie reszt:

b

X

y

u

ˆ

ˆ





Reszty oscylują
wokół zera –
wariancja
składnika
losowego nie
zwiększa się w
czasie

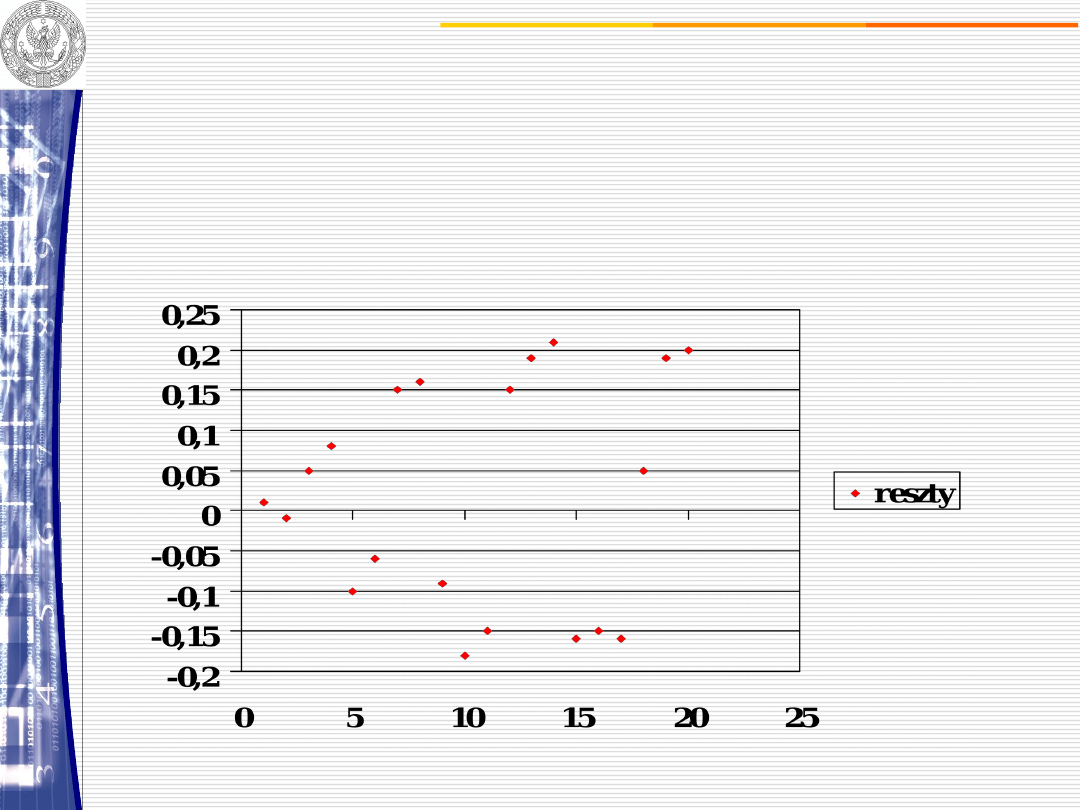
Wariancja składnika losowego nie jest stała – wzrasta w miarę upływu
czasu, a oszacowany model nie jest aktualny. Aby wykorzystać go do
celów predykcji należy go radykalnie poprawić.

DZIĘKUJĘ ZA UWAGĘ

dr inż. Marcin Idzik

Szkoła Główna Gospodarstwa Wiejskiego

Wydział Ekonomiczno - Rolniczy

Katedra Ekonomiki Rolnictwa

i Międzynarodowych Stosunków Gospodarczych

e-mail: [e-mail]