1

7. Rotational

motion

In pure rotation every point of an object moves in a circle

whose center lies on the axis of rotation (in translational motion
the movement occurs along a straight or curved line). In
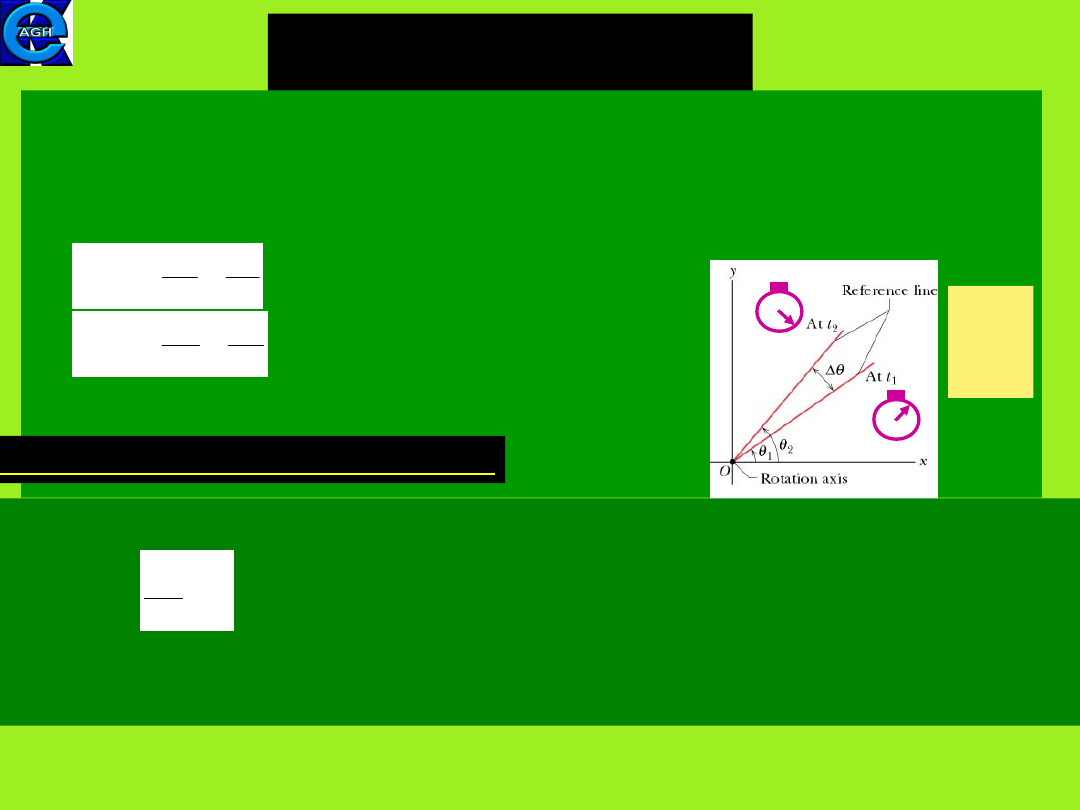
rotational motion one introduces the kinematic angular
variables: angular position θ, angular velocity

ω

and angular

acceleration

α

(7.1)

(7.2)

ω

1

ω

2

t

1

t

2

(figur
e
from
HRW)

7.1. Newton’s law for rotation

dt

d

t

lim

t

















 0

dt

d

t

lim

t

















 0

Second Newton’s law for translational motion

(7.3)

can be transformed to the shape useful for the analysis of rotational motion.
Multiplying both sides of (7.3) by the position vector one obtains





F

dt

p

d

2

Newton’s law for rotation,

cont.

(7.4)

The left side of Eq.(7.4) can be transfomed to

Eq.(7.4) can be then written as

or

(

Newton’second law for rotation

)

(7.5)

where the angular momentum of a particle is

and

is the torque.

The magnitude of torque is
what indicates that in rotation not only the magnitude
of force is important but also how far from the axis
it is applied and in what direction (d-moment arm of F).

F

r

dt

p

d

r

























 













 









































































p

r

dt

d

v

m

r

dt

d

v

m

dt

d

r

v

m

dt

r

d

v

m

dt

d

r

dt

p

d

r

V

V

ecause

b

,



 



0

0























 

F

r

p

r

dt

d









dt

L

d











p

r

L











F

r



Fd

F

r

F

r

t











sin

3

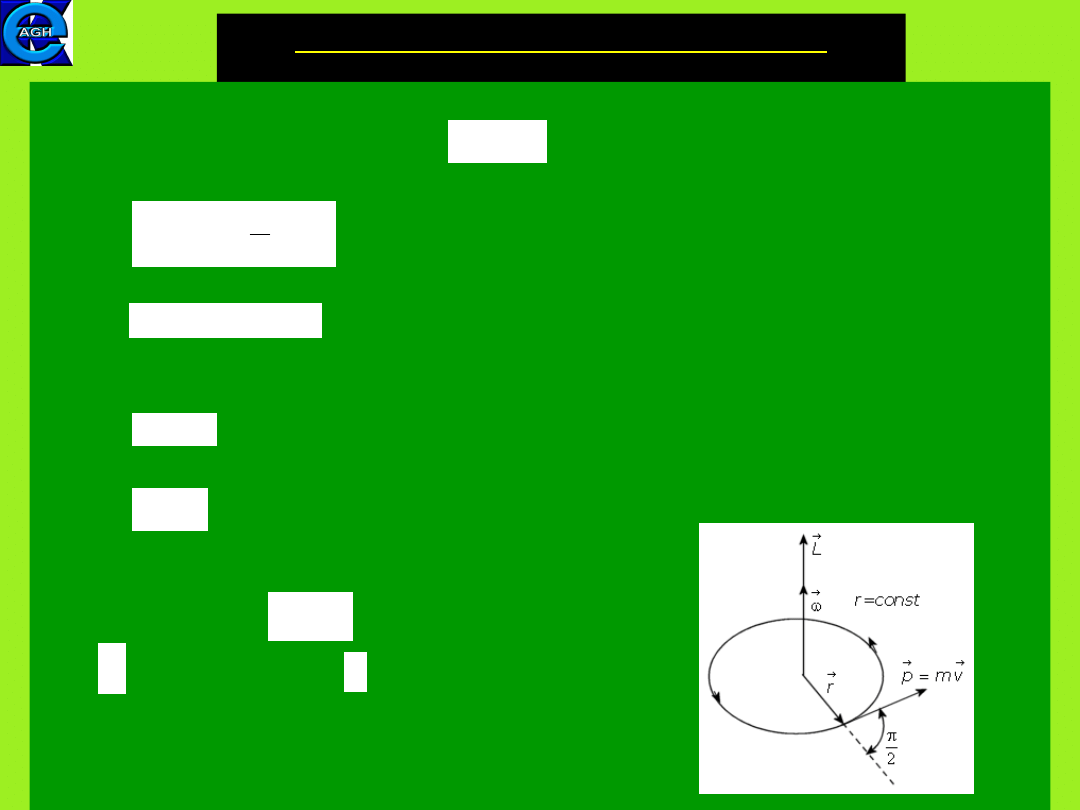
7.2. Flat rotational motion with

constant radius

In the flat rotation with constant r and the reference frame
origin in the center of
a circular path the velocity vector is perpendicular to
the position vector.
In this case we have

The magnitude of an angular momentum is then

(7.6)

The quantity mr

2

in Eq.(7.6) is called the rotational inertia

(moment of inertia) of a particle of mass m rotating about an
axis with a distance r.

(7.7)

The angular momentum (7.6) in a vector form can then be
written as

(7.8)

Eq.(7.8) is formally similar to the equation defining
linear momentum

corresponds to

I corresponds to m

r

r

V











2

sin









r

x

V





2

mr

rmV

L





2

mr

I 









I

L





 V

m

p







V

4

Flat rotational motion with constant

radius, cont.

If the force is placed in a plain of motion, all vectors , ,
are perpendicular
to this plane and the scalar notation can be used.
In this case Eq.(7.5) can be written as follows

or

(7.9)

For I = const Eq.(7.9) transforms to

(7.10)

Eq.(7.10) is the rotational analog of Newton’s second law (F =
ma):

the net torque acting on a particle is equal to the product of the

rotational
inertia about the rotation axis and the resulting angular
acceleration
about that axis.





L











dt

dL

 







dt

I

d









I

dt

d

I

5

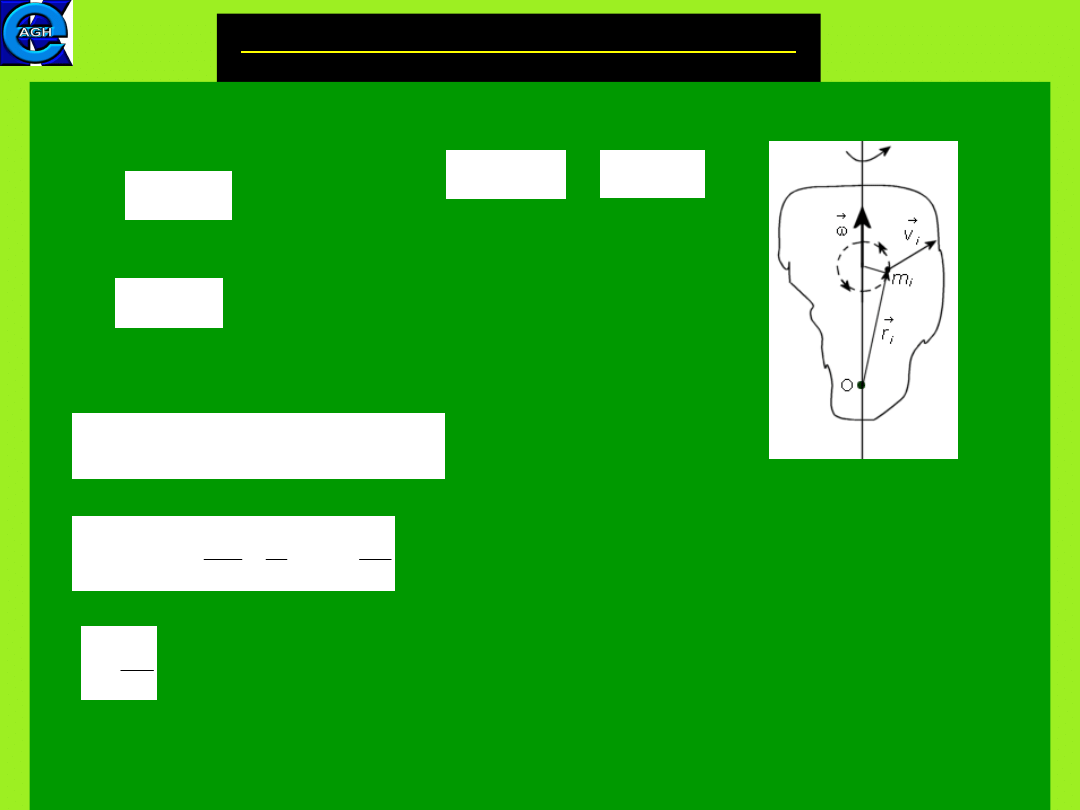
7.3. Rotational motion of a rigid

body

The angular momentum of a small particle m

i

being a part of a

rigid body, with respect to an origin O is equal

where ,

The torque acting on the mass element m

i

vs. origin O is

For the whole rigid body all angular momenta must be
summarized

(7.11)

The net torque is equal

(7.12)

And finally one obtains

(7.13)

The net external torque acting on a rigid body is equal to the
time rate of change
of the total angular momentum of a body.











i

i

i

p

r

L









i

i

i

v

m

p









i

i

r

x

v













i

i

i

F

r



















 

























i

i

i

i

i

i

i

i

i

r

r

m

p

r

L

L



dt

L

d

L

dt

d

dt

L

d

i

i

i

i

i

i





























dt

L

d









6

Rotational motion of a rigid

body, cont.

From (7.13) it follows that

for

(7.15)

This illustrates the

law of conservation of angular momentum: If

the net external torque acting on a system attains zero, the
angular momentum of the system remains constant.

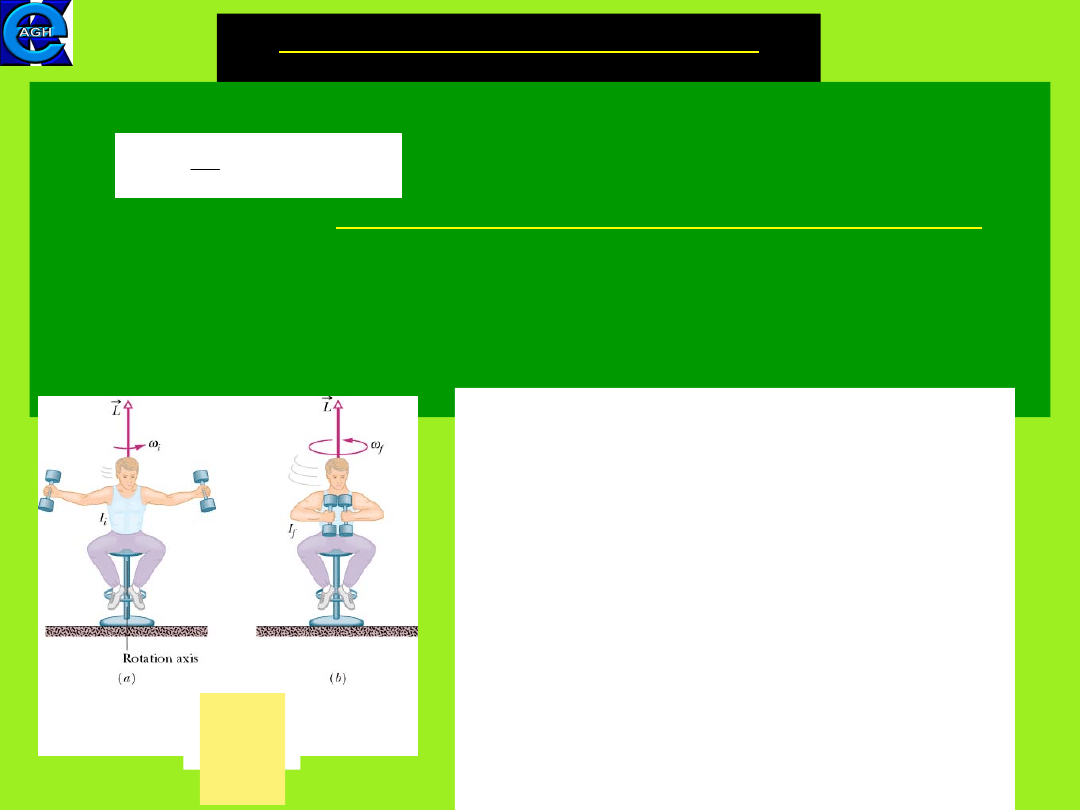
Example 1: the spinning student

const

L

dt

L

d















0

0



Fig(a) A student sitting on a stool and
holding dumbells in his outsstretched
hands, rotates freely about a vertical
axis with an angular
velocity 

i.

Fig(b) The student reduces his
rotational inertia by pulling in his
hands. As no net external torque acts
on the stuent-stool system, the angular
momentum of the system remains
unchanged and the angular speed of
the student increases to 

f

.



f

> 

i

(figur
e
from
HRW)

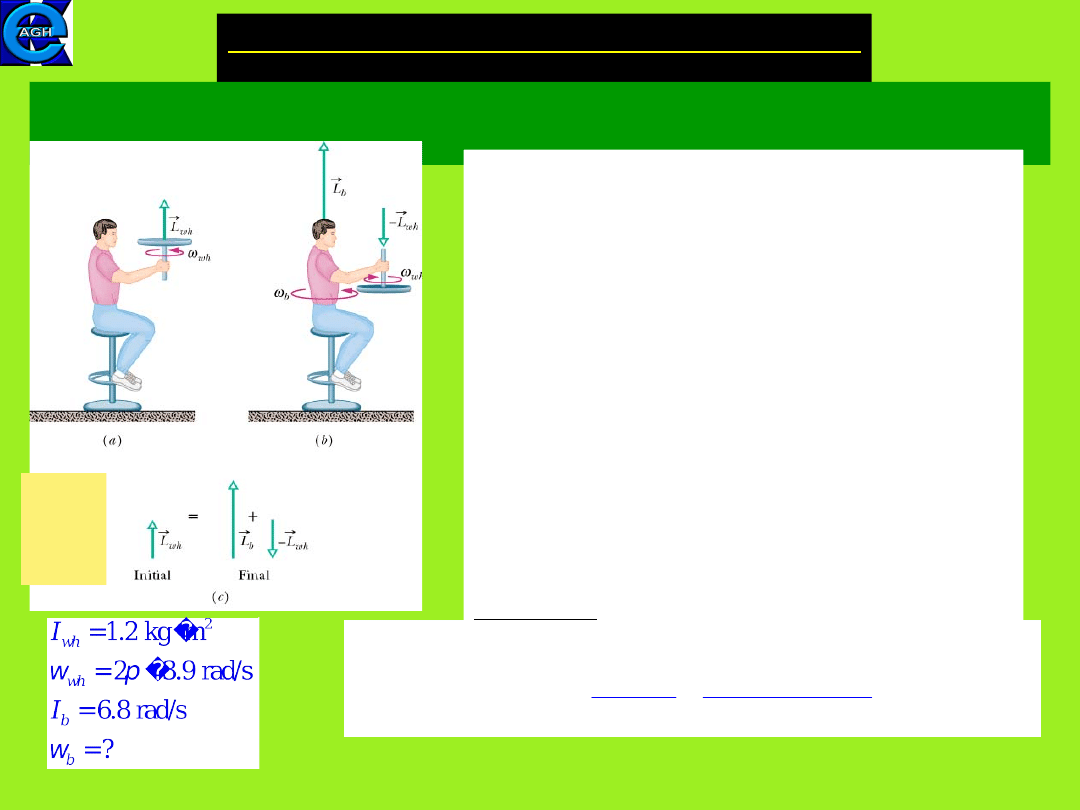
7

Conservation of angular momentum,

cont.

Example 2: a student with a heavy bicycle wheel

Fig(a) A student initially at rest is
sitting on a stool and is holding a
bicycle wheel (with rotational inertia
I

wh

) which rotates counterclockwise

about its central axis with 

wh

.

.

Fig(b) The student inverts the wheel
which now rotates clockwise.

Fig.(c) The net angular momentum of
the system before and after the
inversion remains constant.

Question: With what angular speed 

h

and in what direction does the system
(the student, the stool and the wheel)
rotate after the inversion?

(figur
e
from
HRW)

2

2

2 1.2 2

3.9

2

2

1.4 rad/s

6.8

i

f

wh

wh

b

b

wh

wh wh

b b

wh wh

b

b

L L

L

L

L

L

L

I

I

I

I

w

p

w

w

w

p

=

�

=-

+ �

=

� � �

=

�

=

=

=

�

8

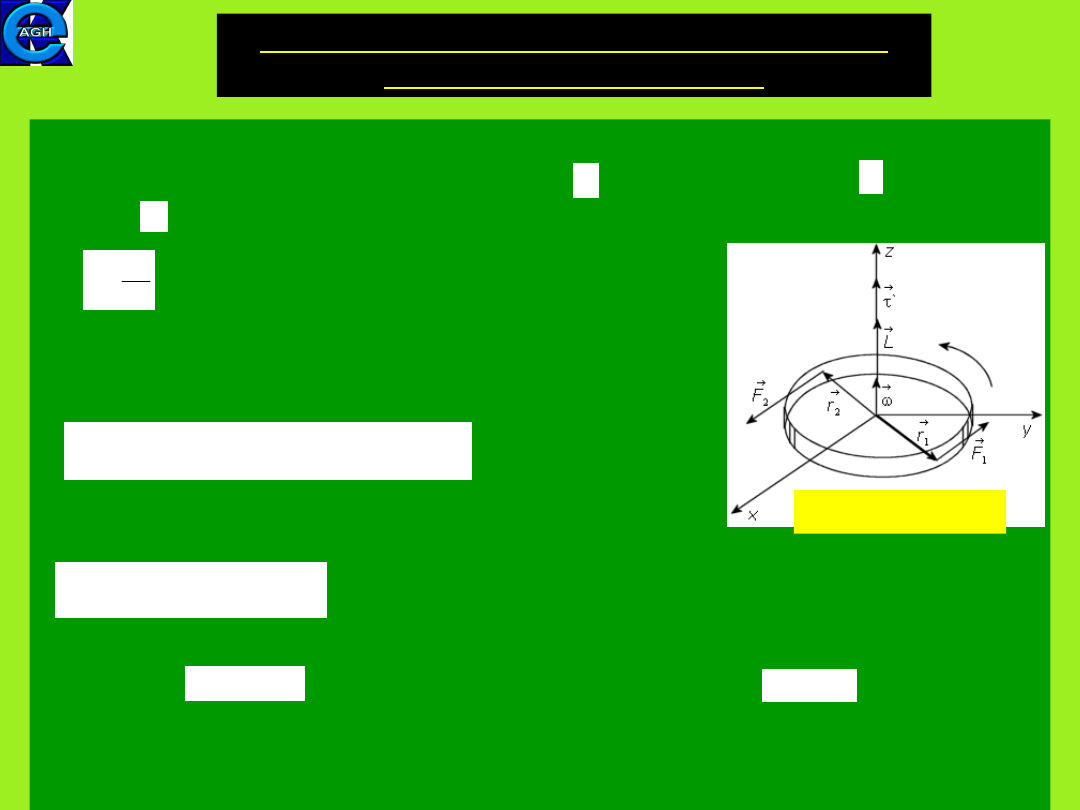
7.4. Rotation of a rigid body about a

fixed symmetrical axis

Equation (7.13) is general but can be simplified if the rotation
takes place about a fixed axis. In this case the vectors of torque
, angular momentum and angular velocity are collinear
and the vector notation can be dropped

(7.16)

An example is the rotation of a hoop about a fixed axis z
passing through its center.
The magnitude of the angular momntum is given by

(7.11)

The summation in the expression for a moment of inertia
can be replaced by integration, what gives

(7.12)

where M is the total mass of a hoop and R its radius. If the
acting forces form a couple, i.e. the torque exerted by
a couple equals where d is
the perpendicular distance between the two forces (in the figure
d = 2r).

dt

dL









L











I

r

m

v

m

r

p

r

L

i

i

i

i

i

i

i

i

i

i















2

2

2

2

MR

dm

R

dm

r

I

M

M











Hoop (obręcz)

F

F

F













2

1

F

d

2





9

7.5. Kinetic energy of rotation about a

fixed symmetrical axis

The kinetic energy of the ith mass point of a rotating rigid body
equals

The total kinetic energy of a body is then

(7.13)

The kinetic energy of a rotating body equals one half the

moment of

inertia multiplied by the square of the angular

velocity.

Eq.(7.13) is the angular equivalent of the expression for the
kinetic energy in translational motion.
In this case

I corresponds to m
ω corresponds to

v

2

2

1

i

i

i

v

m

E 

2

2

2

2

2

2

2

1

2

1

2

1

2

1







I

r

m

r

m

v

m

E

E

i

i

i

i

i

i

i

i

i

i

i

k



















10

7.6. Rotational inertia of selected

bodies

The moment of inertia of a rotating rigid body is calculated from

the expression

(

7.14

)

r – the distance of mass dm from the axis of

rotation

When the body has uniform density, ρ, one can write dm =

ρ

dV

and integral (7.14) transforms to

(7.15)

The integration in (7.15) is over volume V but for the

symmetrical objects the calculation in many cases can be
reduced to, e.g. integration over one dimension only.

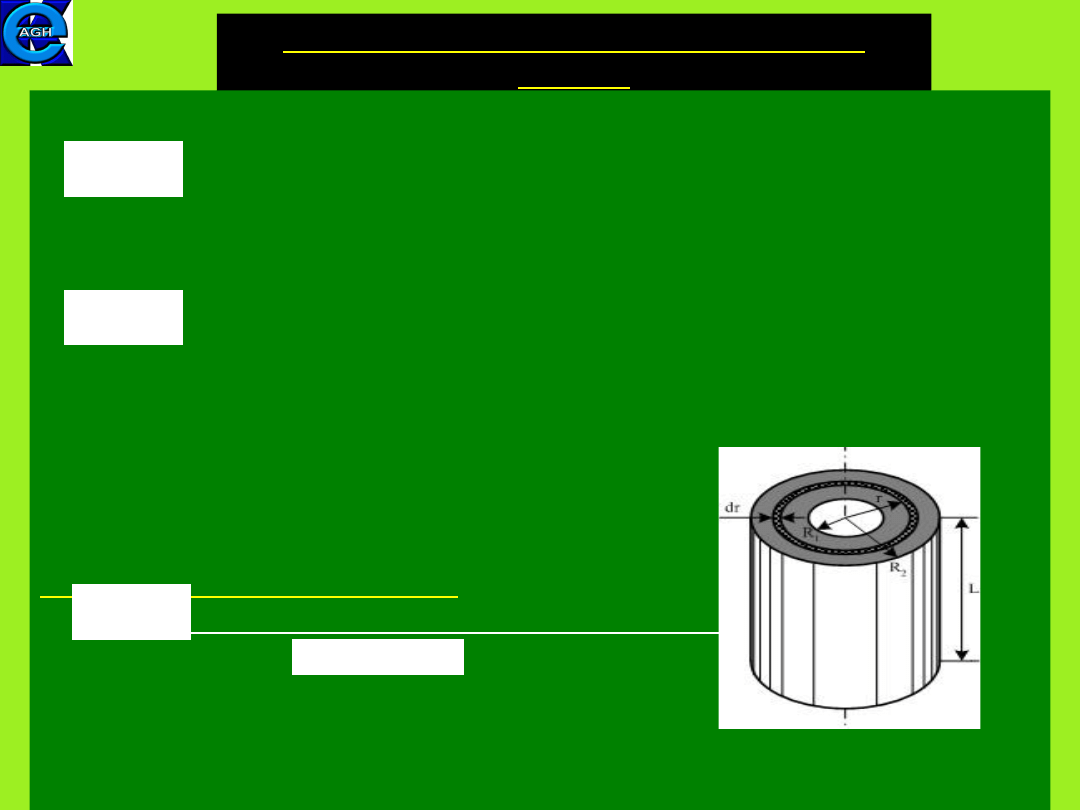
Examples of calculations

1. Annular cylinder (ring) about central axis

where

is the volume

of a thin ring of radius r, thickness dr and height h.
The limits of integration are R

1

and R

2

.





M

dm

r

I

2





V

dV

r

I

2







V

dV

r

I

2







L

rdr

dV







2

11

Annular cylinder,

cont.

Finally one obtains

(7.16)

From (7.16) it follows that for a solid cylinder (R

1

= 0) we obtain

(the height L is not important so it also holds for a

flat disk)

Again, for the case (cylinder) one obtains from (7.16)

what is in accordance with expression (7.12) for the moment of

inertia of a hoop.











2

4

2

4

2

2

2

2

1

2

2

2

1

2

2

2

1

2

2

4

1

4

2

1

2

4

3

2

2

1

2

1

R

R

R

R

L

R

R

M

L

R

R

L

R

R

r

L

dr

r

L

rLdr

r

I

R

R

R

R



















































2

2

1

2

2

R

R

M

I





2

2

MR

I 

R

R

R





2

1

2

MR

I 

12

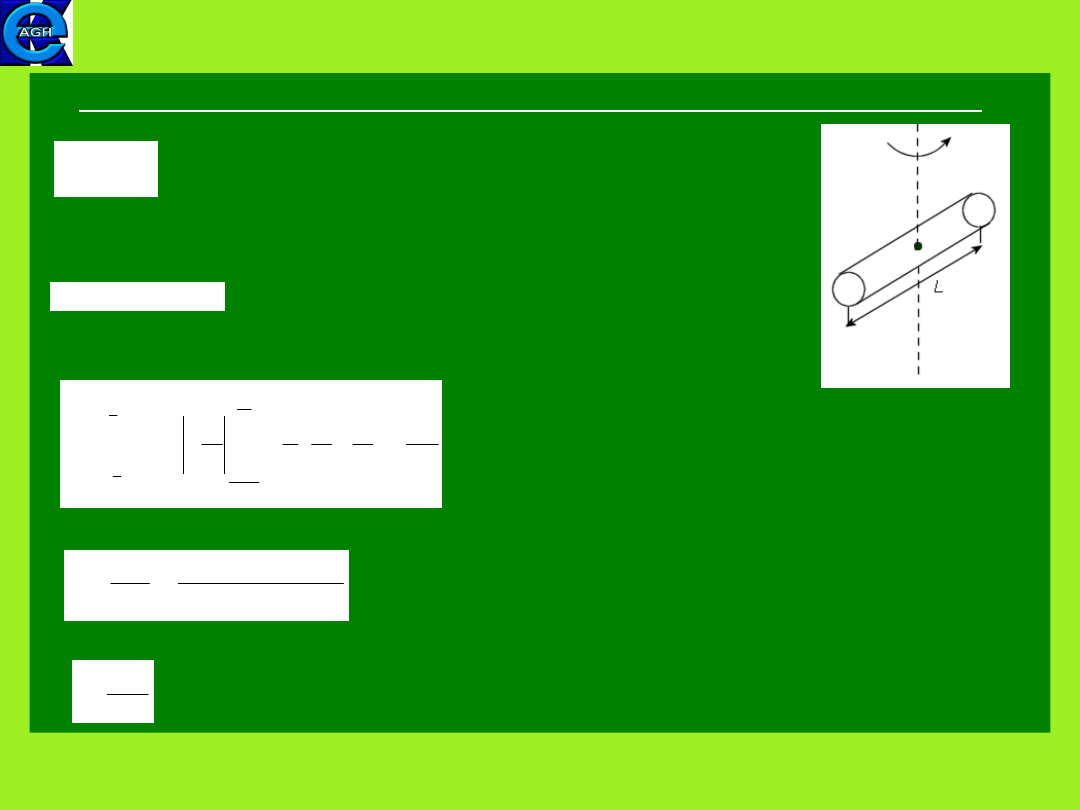
2.

Thin rod about axis through center perpendicular to lenght

(7.17)

For this case one can introduce the linear density λ. Thus

The moment of inertia is then equal

Making use of the introduced linear density

one obtains the final result

(7.18)





M

dm

r

I

2

dr

dl

dm









12

8

8

3

2

2

3

3

3

3

3

2

2

2

L

L

L

L

L

r

dr

r

I

L

L





































12

2

ML

I 

L

length

s

'

rod

M

mass

s

'

rod

dl

dm







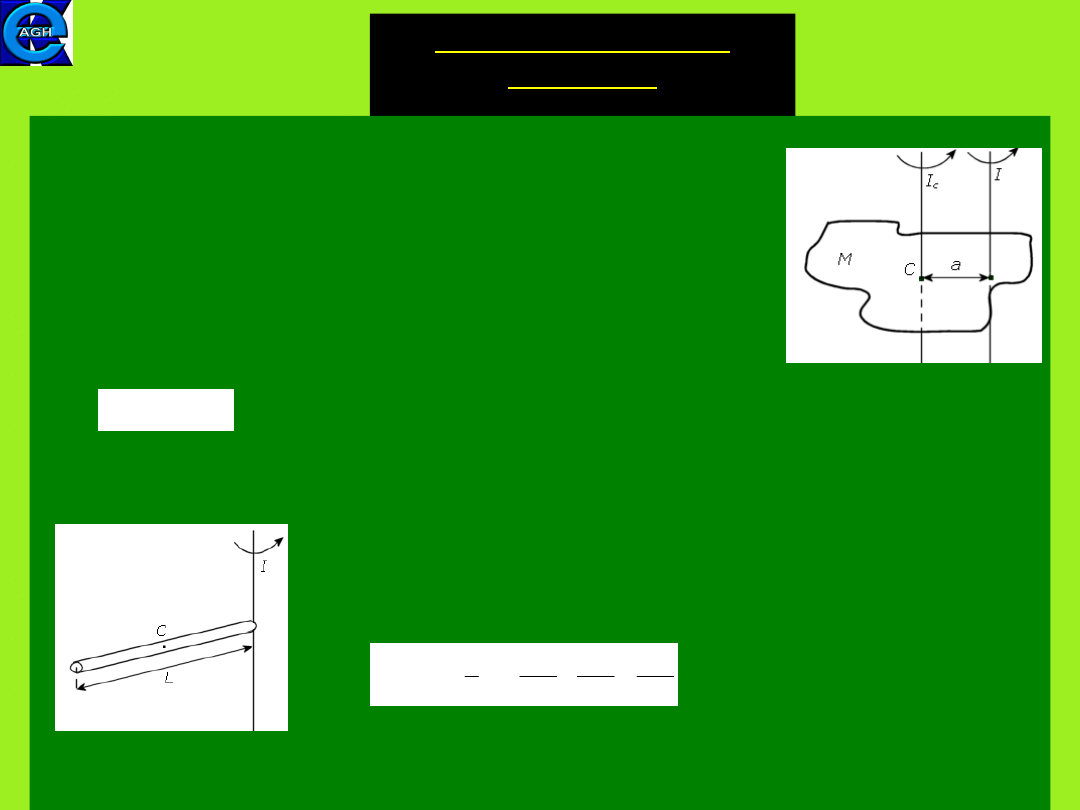
13

7.7. Parallel Axis

Theorem

(twierdzenie Steinera)

The question is how to determine the moment of
inertia about a given axis, which does not pass through
the center of mass of a body.
The

parallel-axis theorem

states that:

If the moment of inertia about an axis passing thorough

the center of mass I

C

is known, then the moment of inertia

about any other parallel axis I is given by

(7.19)

where

a

is the distance between the two parallel axes and M is

the mass of a body.

Sample problem

What is the moment of inertia of a rod about

an axis

perpendicular to the rod and

passing through its end?

From the parallel-axis theorem one gets

2

Ma

I

I

C





3

4

12

2

2

2

2

2

ML

ML

ML

L

M

I

I

C





















