Teoria kolejek i analiza
potoków ruchu

Piotr Januszewski
Łukasz Miśkiewicz

Potok ruchu

Jest to odwzorowanie
przemieszczania się ładunku, ludzi
lub informacji w systemie
transportowym.

Potok ruchu mierzy się w
jednostkach transportowych, jako
liczbę jednostek transportowych na
jednostkę czasu.

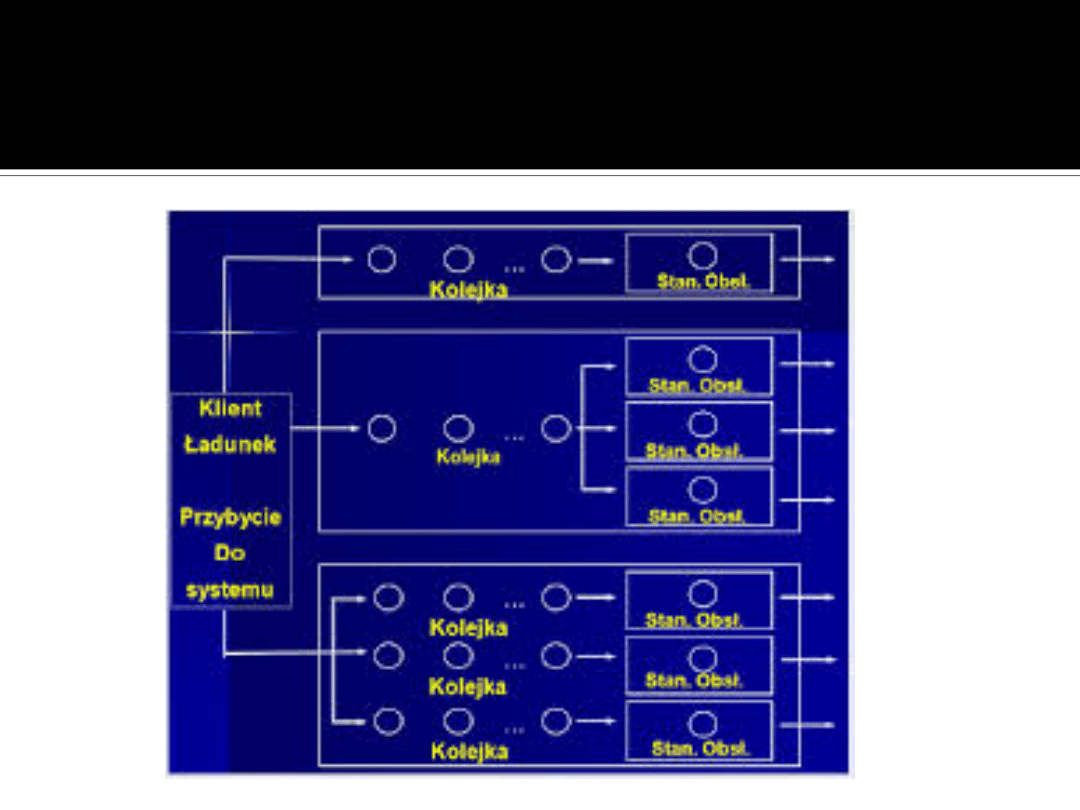
Schematy kolejek

[3]

Zjawiska przy tworzeniu się
kolejki



Balking – przymusowe bądź
nieprzymusowe opuszczanie kolejki,



Reneging – wycofywanie się z kolejki,



Jockeying – zmiana kolejki w czasie.

Definicja teorii kolejek

Teoria kolejek (masowej obsługi) jest
dziedziną matematyki zajmującą się
analizowaniem systemów, w
których powstają kolejki. Przy jej
pomocy można opisywać procesy
prowadzące do tworzenia się kolejek
oraz analizować ich obsługę. [1]

Charakterystyka modeli teorii
– reguła kolejności obsługi



FIFO (First In, First Out),



SIRO (Service in Random Order),



LIFO (Last in, First Out)

Procesy ruchu drogowego
opisywane przez teorię
masowej obsługi



Tworzenie się kolejek pojazdów na:



zwężeniach dróg,



wlotach na skrzyżowania,



wjazdach na punkty poboru opłat,



wjazdach oraz wyjazdach z parkingów.

Schemat Kendall’a



A/B/m



A – rozkład zmiennej losowej w procencie
zgłoszeń,



B – rozkład zmiennej losowej, zgodnie z którą
następuje obsługa,



m – liczba stanowisk obsługi



Za A i B podstawia się:



M dla rozkładu wykładniczego,



D dla zgłoszeń,



Ek dla rozkładu Erlanga



Kwestia analizy przydatności systemu

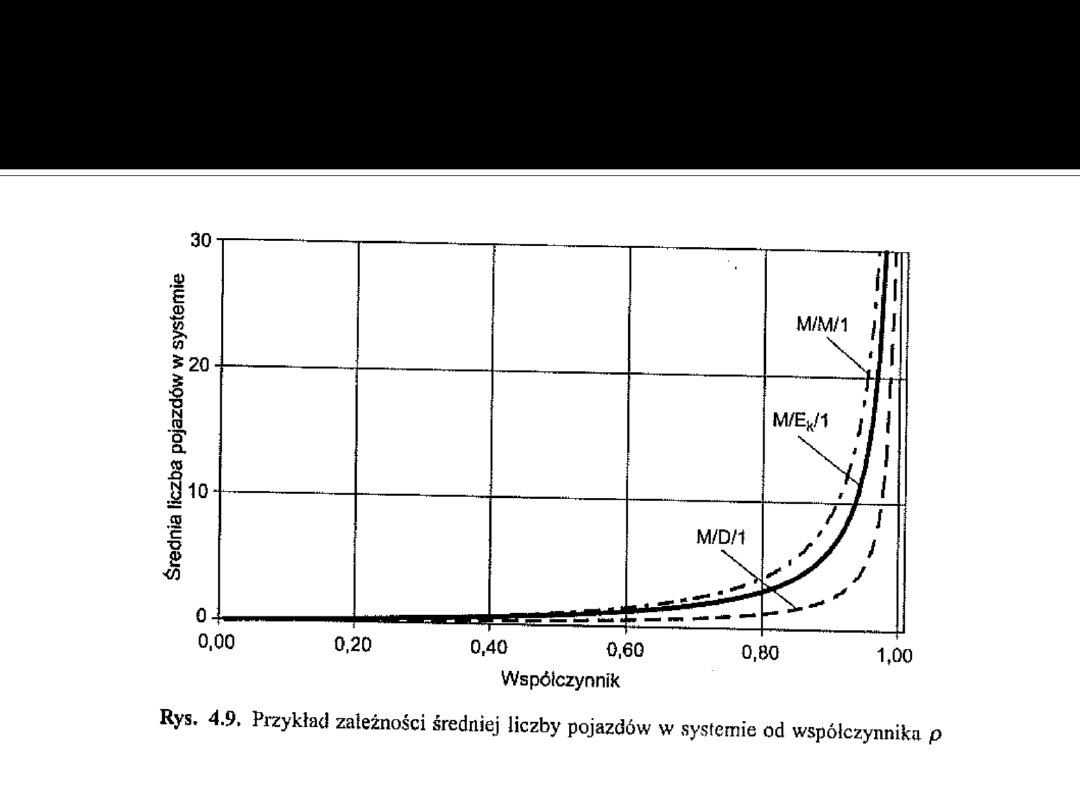
Współczynnik ρ (stan
kolejki)

[1]

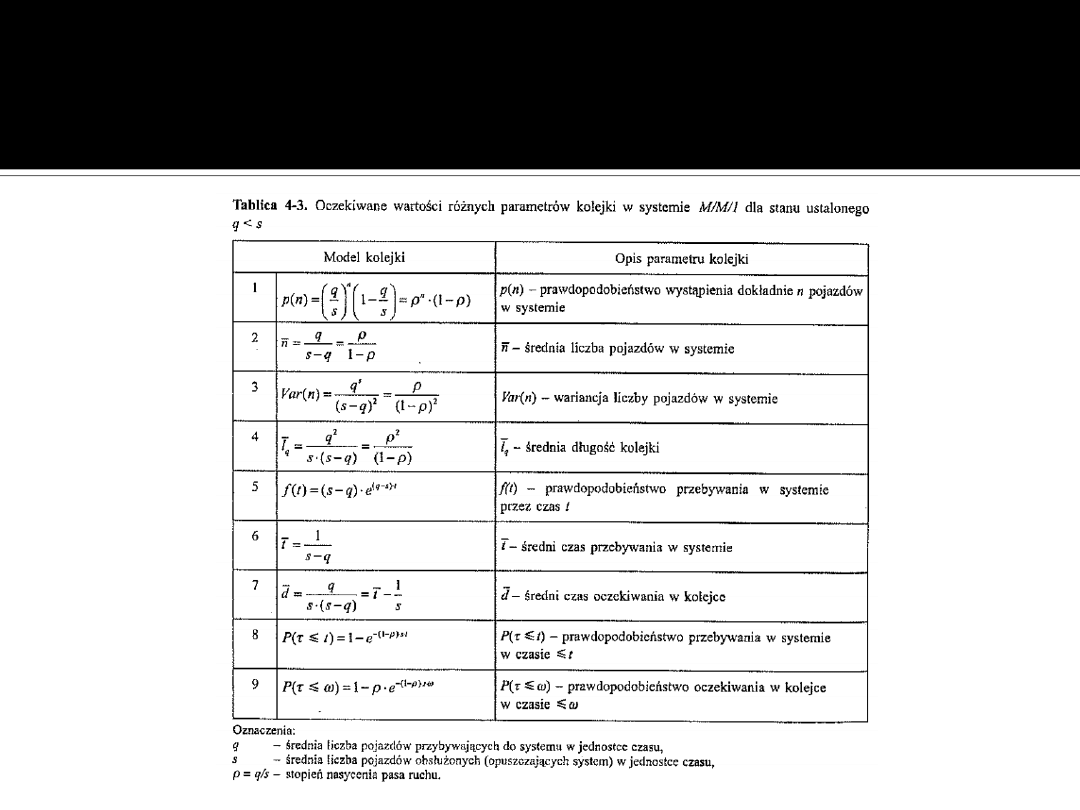
Parametry kolejki

[1]

Parametry systemu
kolejkowego



λ – intensywność napływu zgłoszeń,



μ – intensywność obsługi zgłoszeń,



– średni czas między kolejnymi
zgłoszeniami,



- średni czas obsługi pojedynczego
zgłoszenia,



- obciążenie systemu

< 1 – warunek stabilności systemu



 

Parametry ważne z punktu
widzenia użytkownika [2]



Długość systemu



Długość kolejki



Czas oczekiwania w systemie



Czas oczekiwania w kolejce

Zadanie 1

Znając średnią liczbę samochodów
przybywających λ = 700 s/h oraz średnią
liczbę samochodów opuszczających μ = 800
s/h oblicz dlaczego kierowca zapłaci za
przejechanie odcinka na autostradzie A1
pomiędzy Rusocinem a Kopytkowiem 11,30
zł

Zadanie 1

Wiedząc, że średnią liczba samochodów
przybywających odcinek drogi to λ = 700
sam/h, a średnia liczba samochodów
opuszczających odcinek drogi μ = 800
sam/h, oblicz średni czas oczekiwania d w
kolejce oraz średnią długość kolejki l .

ρ=λ/μ l=



 

Rozwiązanie 1 -
rozwiązanie

ρ=0,875

d=
l



 

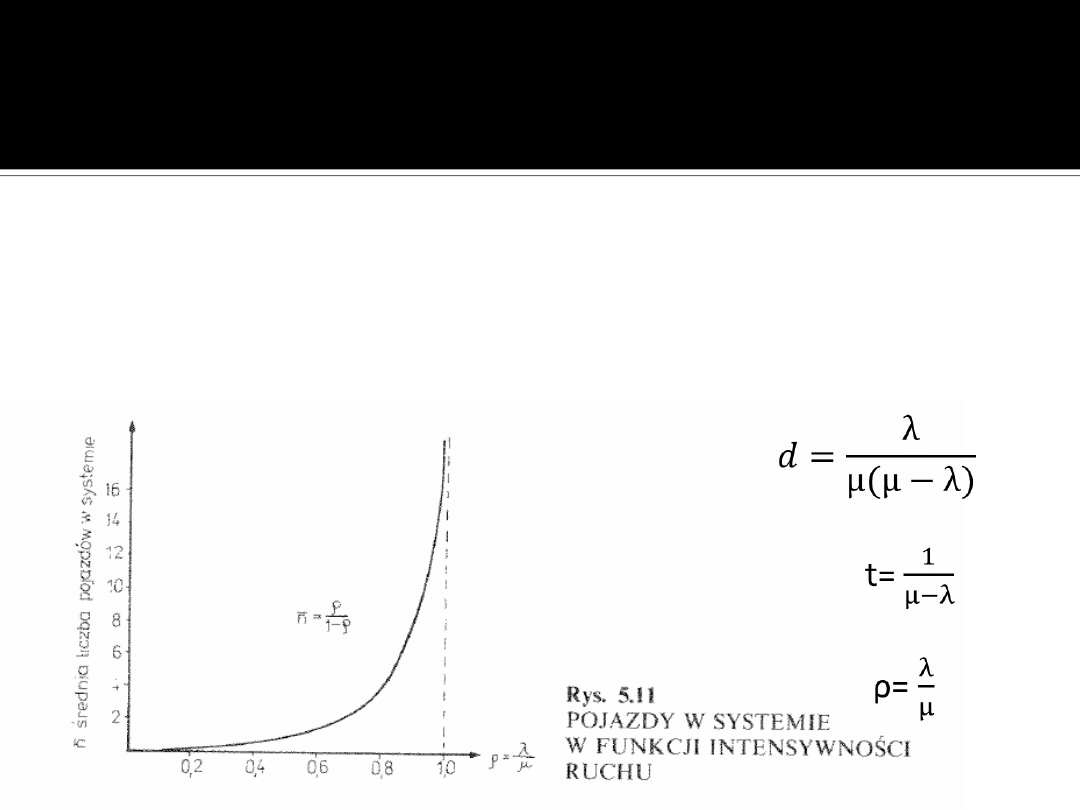
Zadanie 2

Na podstawie wykresu oraz wiedząc że średni czas
przebywania w systemie t= 15 sek , oblicz czas
oczekiwania w kolejce przy założeniu, że liczba
pojazdów wynosi n=4.

t=

ρ=

 

[3]

Zadanie 2 - rozwiązanie

Dla n=4 => ρ=0,8



 

Zadanie 3

Na odcinku drogi dwujezdniowej są dwa pasy
ruchu,

jeden

przeznaczony

dla

wszystkich

pojazdów, a drugi, mniejszy dla rowerów. Ruch
samochodowy w jest tak duży, że rozważa się
możliwość przebudowy pasa rowerowego na
kolejny pas ruchu dla pojazdów samochodowych i
tym samym przeniesienie drogi dla rowerów obok.
Sprawdzić, czy jest to słuszna decyzja. Podano
obserwacje poczynione w czasie godziny szczytu
dla pojedynczego pasa ruchu dla pojazdów,
przedstawione w tabeli. [4]

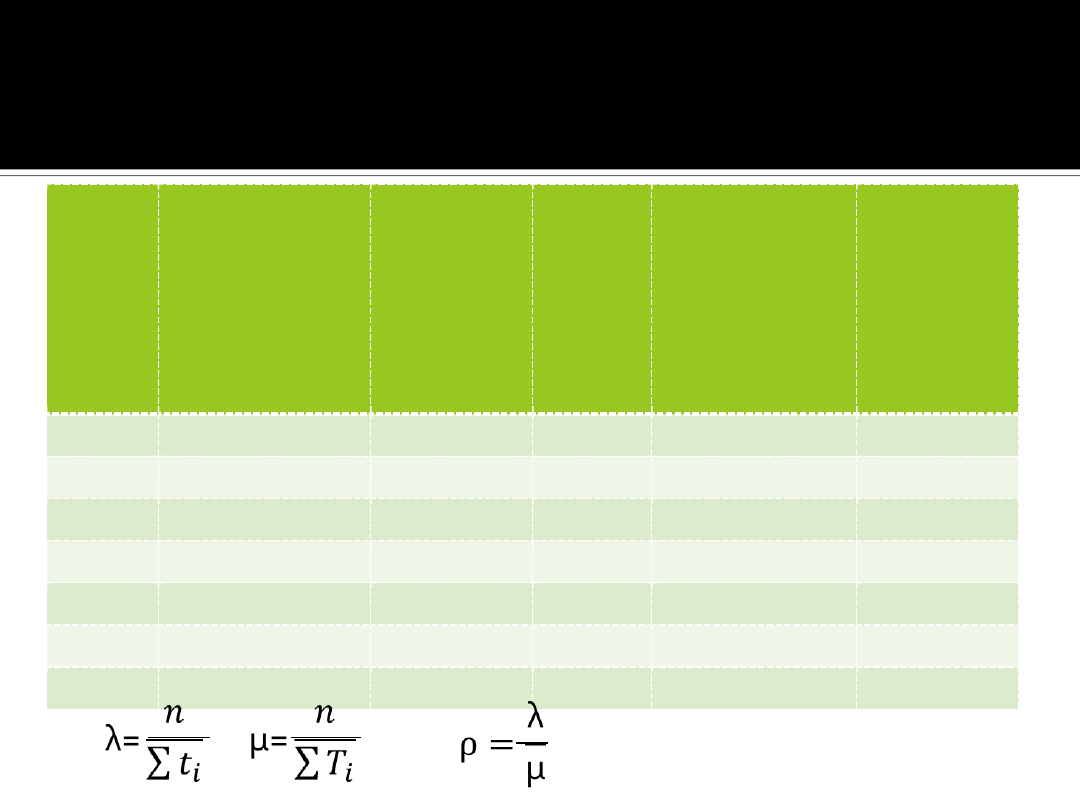
Zadanie 3 - dane

Pojaz

d nr

Czas

przybycia

liczony od

przybycia

poprzednieg

o pojazdu t

[s]

Czas

obsługi

pojazdu

T [s]

Pojaz

d nr

Czas

przybycia

liczony od

przybycia

poprzednie

go pojazdu

t [s]

Czas

obsługi

pojazdu

T [s]

1

0,0

1,5

7

1,0

3,0

2

0,8

1,0

8

1,2

2,5

3

1,5

0,8

9

1,8

1,2

4

2,0

0,6

10

2,0

0,8

5

0,8

1,0

11

0,6

1,5

6

0,7

1,5

12

1,4

2,2

SUMA

?

?

λ= �

∑

�

�

 

μ= �

∑

�

�

 

ρ=

λ
μ

 

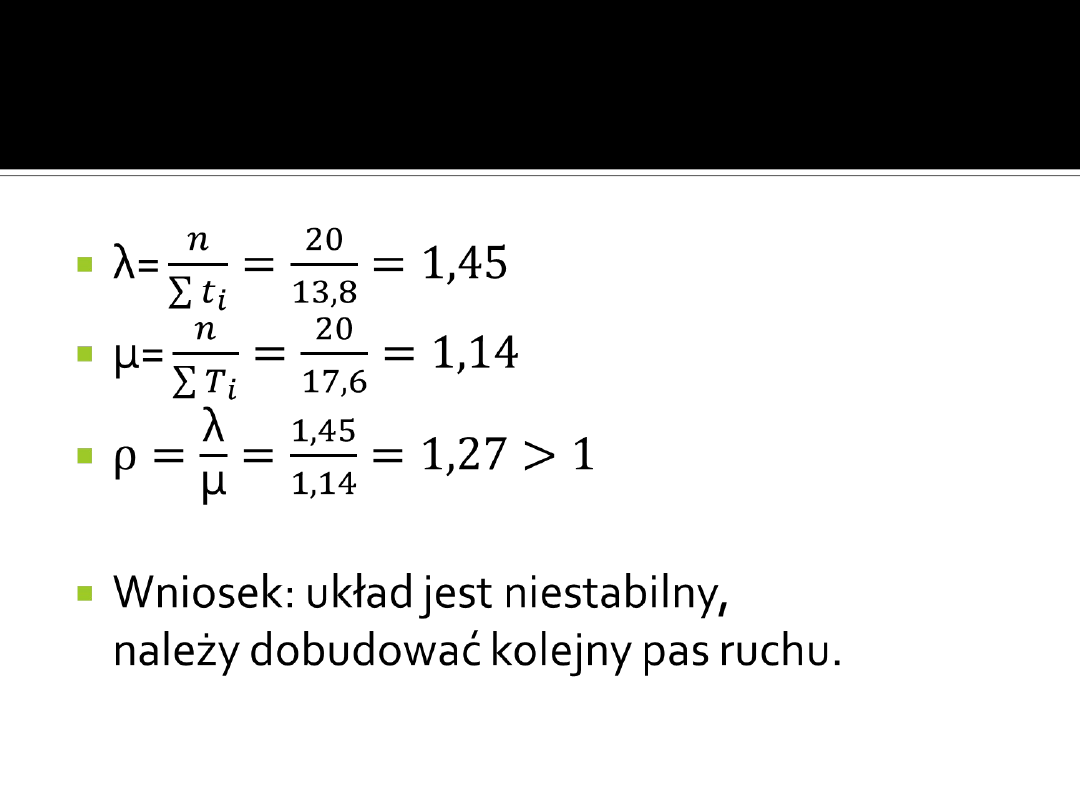
Zadanie 3 - rozwiązanie





Wniosek: układ jest
niestabilny, należy dobudować
kolejny pas ruchu.



 

Bibliografia



[1] Gaca Stanisław, Tracz Marian,
„Inżynieria Ruchu”



[2] youtube.com



[3]
oizet.p.lodz.pl/istan/dydaktyka/badan
ia/



[4] mfiles.pl