PRZEPŁYWY W SIECIACH.
TWIERDZENIE
MINIMAKSOWE.

Mateusz Chenc
14.10.2011r.

Plan prezentacji



Sieci przepływowe



Przepustowość



Przepływ



Ścieżka residualna



Przekrój

Sieć przepływowa

Przez sieć przepływową (ang. flow

network) będziemy rozumieli spójny graf
skierowany G=(V,E) (ang. connected
directed graph lub conected digraph), w
którego krawędziach odbywa
się przepływ (ang. flow) jakiegoś czynnika.
W sieci przepływowej wyróżnia się jeden
wierzchołek s, z którego wychodzą przepływy
- jest to tzw. źródło (ang. source), oraz jeden
wierzchołek t, do którego zbiegają się
przepływy - jest to tzw. ujście (ang. sink).

Przepustowość

Z każdą krawędzią grafu (w terminologii sieci

przepływowych krawędzie nazywamy kanałami -
ang. chanels) skojarzony jest parametr
określający tzw. przepustowość (ang.capacity),
która oznacza maksymalną ilość czynnika
mogącego przez tę krawędź przepływać.
Przepustowość jest nieujemną funkcją rzeczywistą
oznaczaną zwykle przez c(u,v), gdzie u i v ∈
V. Jeśli wierzchołki u i v są połączone kanałem,
czyli (u,v) ∈ E, to przepustowość tego kanału
spełnia warunek c(u,v) ≥ 0. Jeśli wierzchołki u i v
nie są połączone kanałem, czyli(u,v) ∉ E,
to c(u,v) = 0.

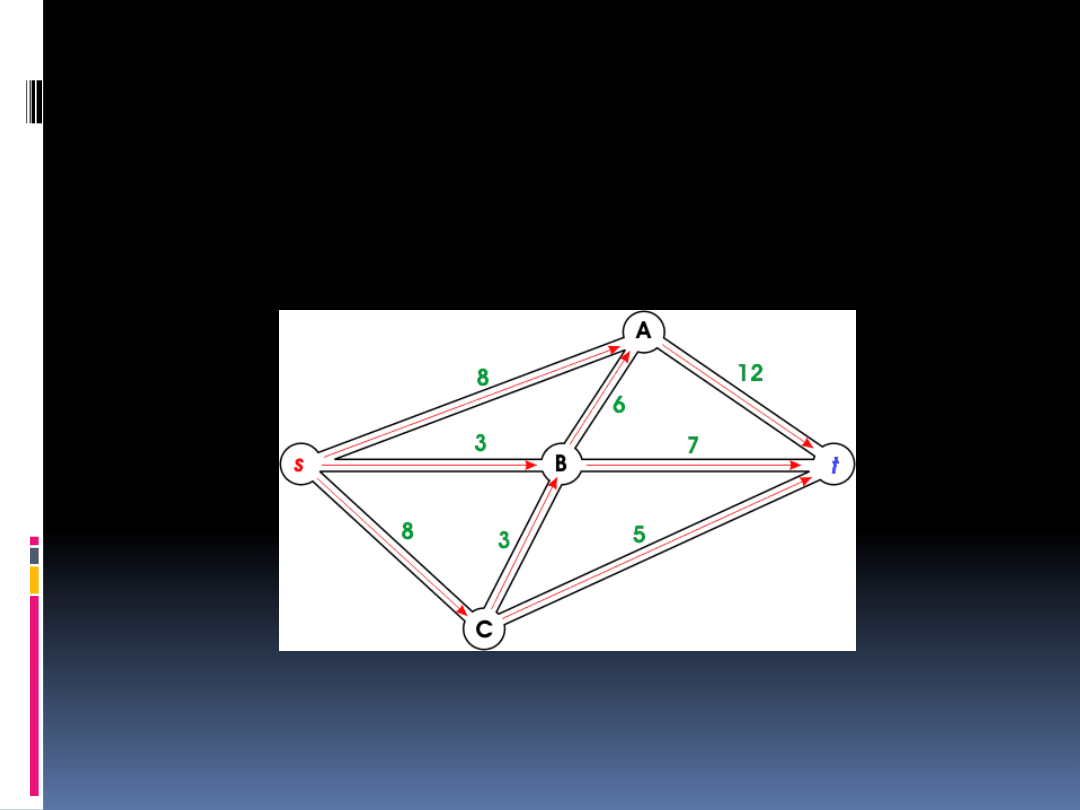
s-źródło,
t-ujście,
A,B,C- wierzchołki pośredniczące

Przepływ

Przepływ to funkcja rzeczywista o
argumentach będących parą
wierzchołków grafu, oznaczana
zwykle przez f(u,v). Funkcja
przepływu musi spełniać trzy
warunki.
Funkcję f(u,v)
nazywamy przepływem netto (ang.
net flow) od wierzchołka u do
wierzchołka v. Funkcja ta może
przyjmować wartości dodatnie i
ujemne.

Warunkek I
Ograniczenia przepustowości (ang. capacity constraints)



Dla każdej pary wierzchołków u i v ∈ V
zachodzi f(u,v) ≤ c(u,v).



Warunek ten mówi, iż przepływ w kanale
(u,v) ∈ E nie może przekroczyć jego
przepustowości. Zwróć uwagę, iż z
warunku tego i własności przepustowości
kanału wynika od razu, iż jeśli pomiędzy
wierzchołkami u i v nie ma kanału, to
przepływ f(u,v) = 0, ponieważ c(u,v) = 0.

Warunek II
Skośna symetria (ang. skew symmetry)



Dla każdej pary wierzchołków u i v ∈
V zachodzi f(u,v) = -f(v,u). Warunek
ten oznacza, iż przepływ w
odwrotnym kierunku jest ujemny. Z
warunku tego wynika od razu, iż
f(u,u) = -f(u,u) = 0 - przepływ
pomiędzy tym samym wierzchołkiem
grafu jest zawsze zerowy.

Warunek III
Zachowanie przepływu (ang. flow conservation)



Dla każdego wierzchołka u ∈ V - {s,t}
suma wszystkich przepływów f(u,v), v
∈ V, jest równa zero. Warunek ten
oznacza, iż suma wszystkich
przepływów wpływających do
wierzchołka jest równa sumie
przepływów wypływających z
wierzchołka.

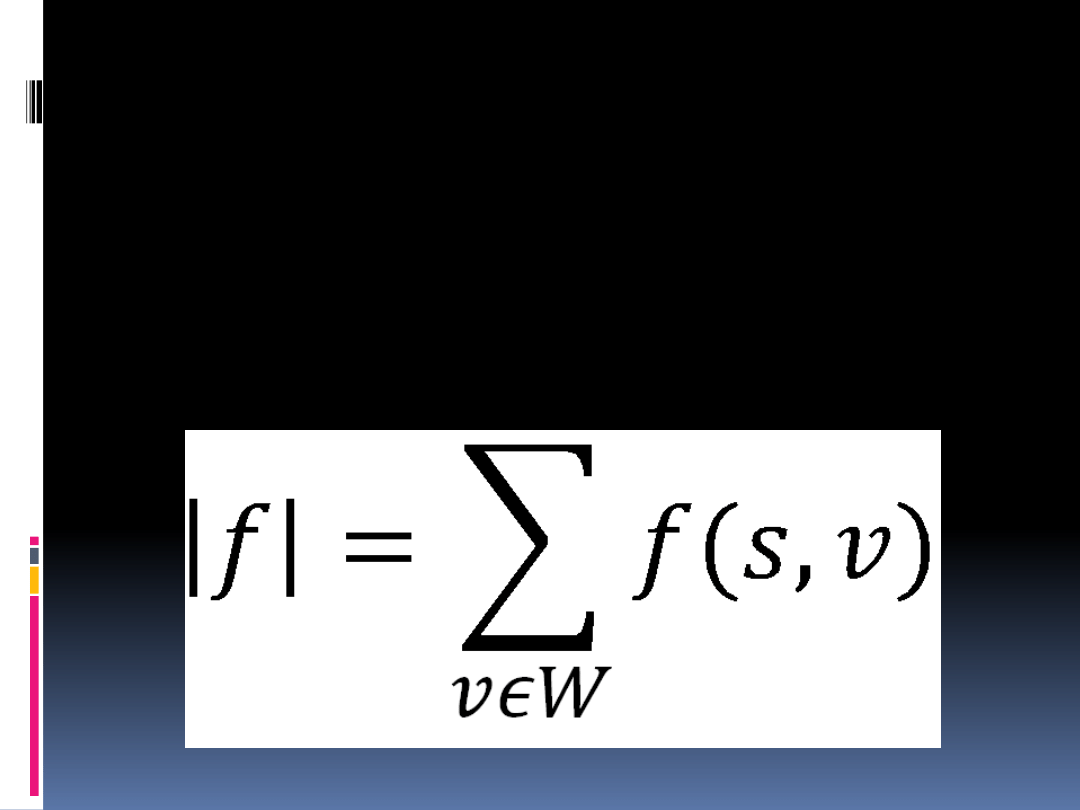
Przepływ sieci

Przepływ sieci jest definiowany jako

suma przepływów netto ze
źródła s do wszystkich pozostałych
wierzchołków sieci:

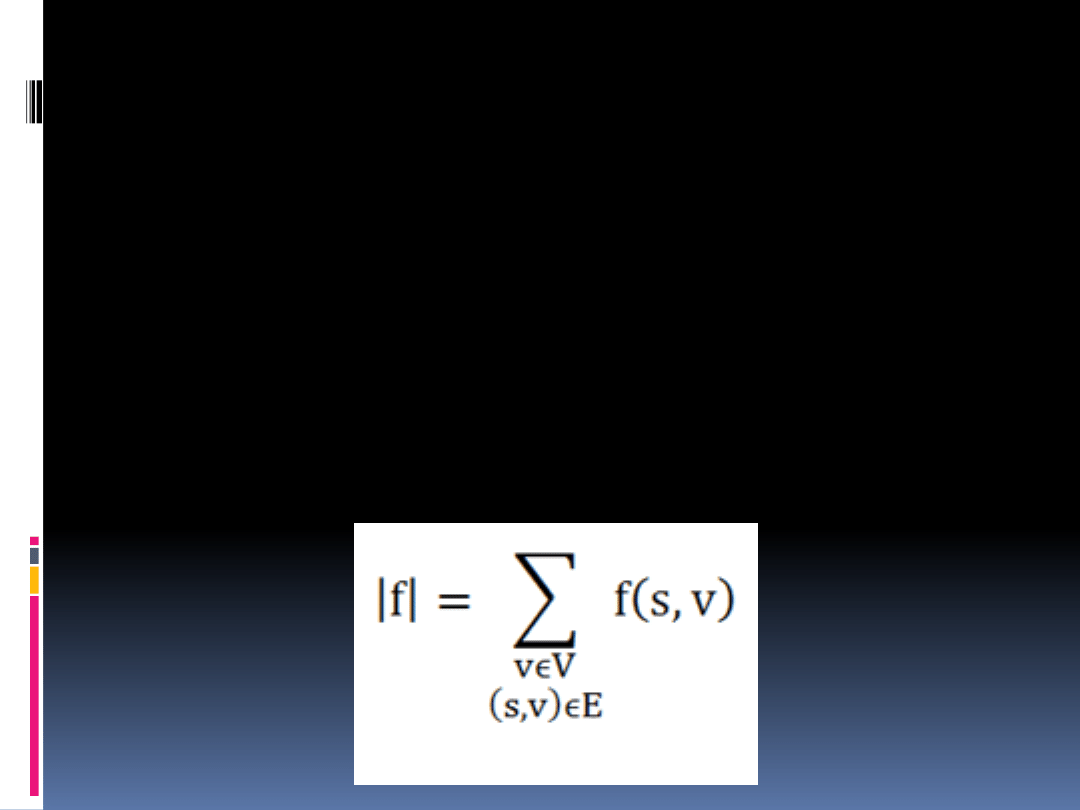
Przepływ netto

Ponieważ przepływ netto f(u,v) = 0,
jeśli pomiędzy wierzchołkami u i v
nie istnieje kanał, to przepływ sieci
można w prosty sposób określić
sumując przepływy netto z
wierzchołka s do wszystkich jego
sąsiadów, czyli:

Przykład



Niech N=(V,c) będzie siecią taką, że
V={u,v,w,x,y} oraz c(uy)=7,
c(vw)=1, c(vy)=1, c(wu)=3,
c(wx)=2, c(wy)=2, c(xu)=4, c(xv)=3,
c(xw)=3, a wszystkie pozostałe
przepustowości są zerami.

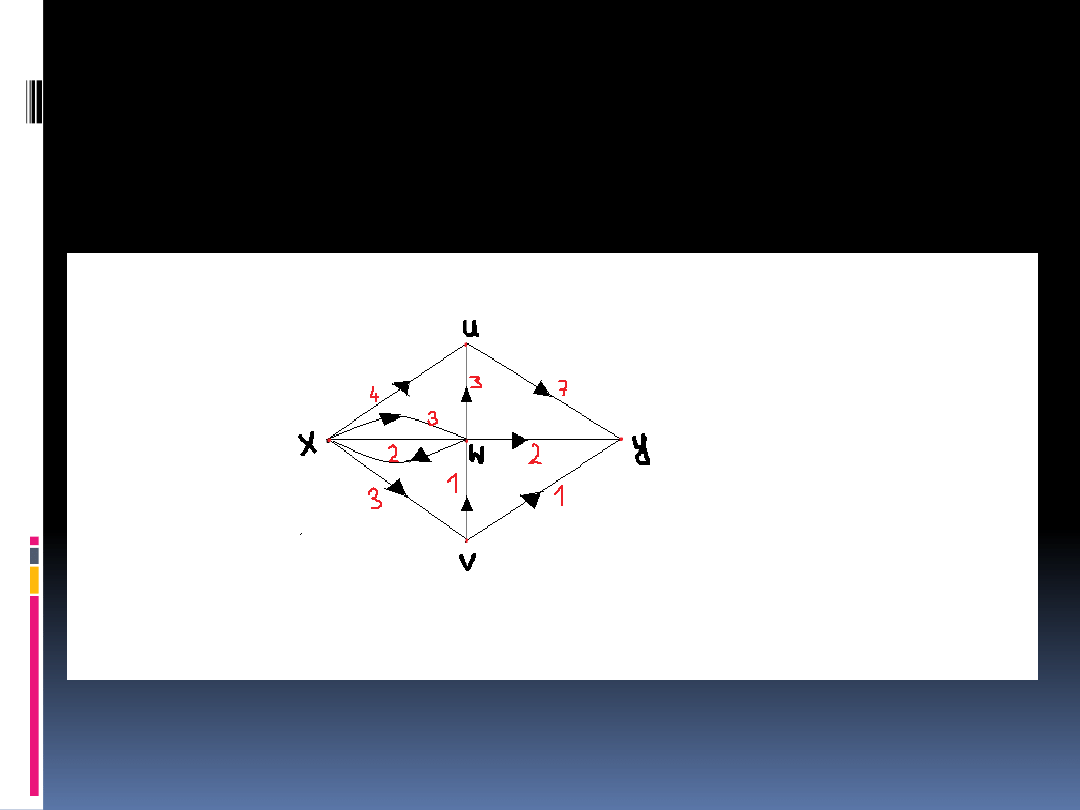
Przykład

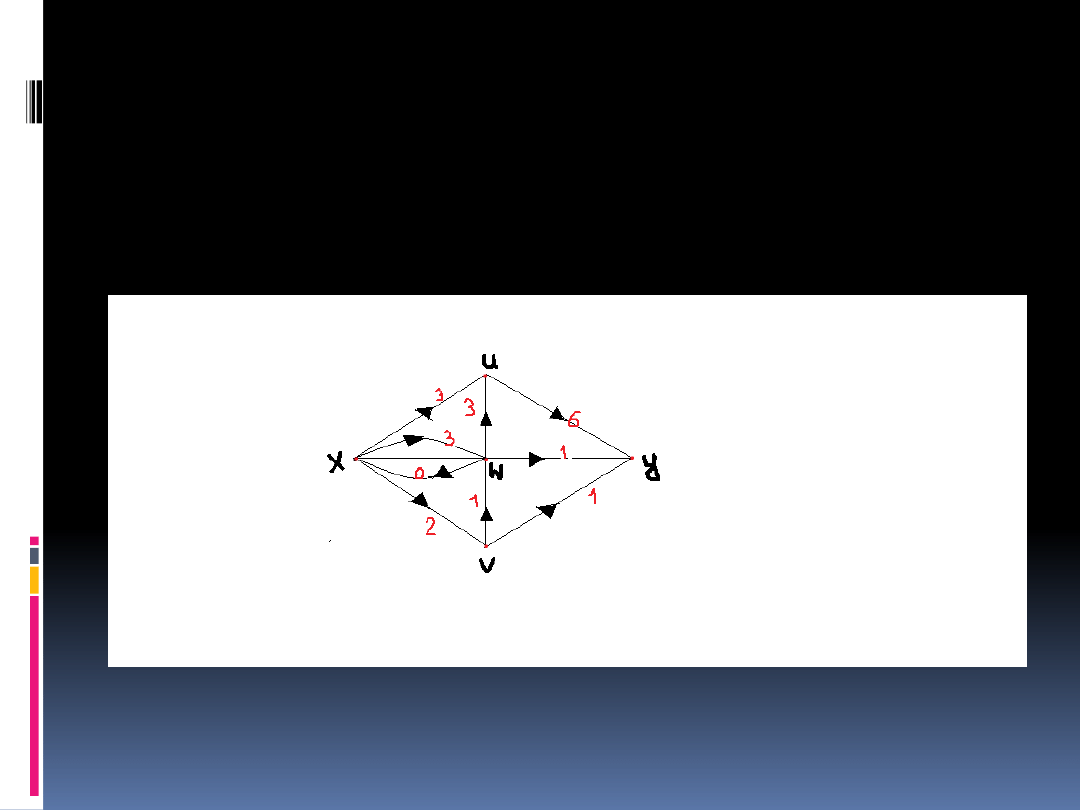
Pamiętając o tym, że „przepływ” nie może
być większy od zdefiniowanej
przepustowości, wyznaczamy przykładowe
„przepływy”:

Sieć residualna

Przepustowość residualna c

(u,v) (ang. residual

capacity) danego kanału (u,v) jest równa różnicy
przepustowości oraz przepływu w tym kanale:
c

(u,v) = c(u,v) - f(u,v)

Przepustowości residualne liczy się również w
kierunku przeciwnym - pomimo, że w sieci może nie
występować kanał zwrotny. W takim przypadku,
zgodnie z definicją przepustowości i własnością
skośnej symetrii przepływu, mamy:
c

(v,u) = c(v,u) - f(v,u)

Ponieważ c(v,u) = 0, f(v,u) = - f(u,v), to
c

(v,u) = 0 - (-f(u,v)) = f(u,v)

Sieć residualna

Przepustowości residualne indukują tzw. sieć
residualną (ang. residual network) , która
zawiera wszystkie wierzchołki oryginalnej
sieci przepływowej oraz krawędzie łączące
wierzchołki, dla których przepustowość
residualna jest większa od zera - oznacza to,
iż w sieci residualnej nie umieszczamy
krawędzi pomiędzy wierzchołkami u i v, jeśli
c

(u,v) = 0. Na poniższym rysunku

przedstawiamy sieć residualną dla
przykładowej sieci przepływowej:

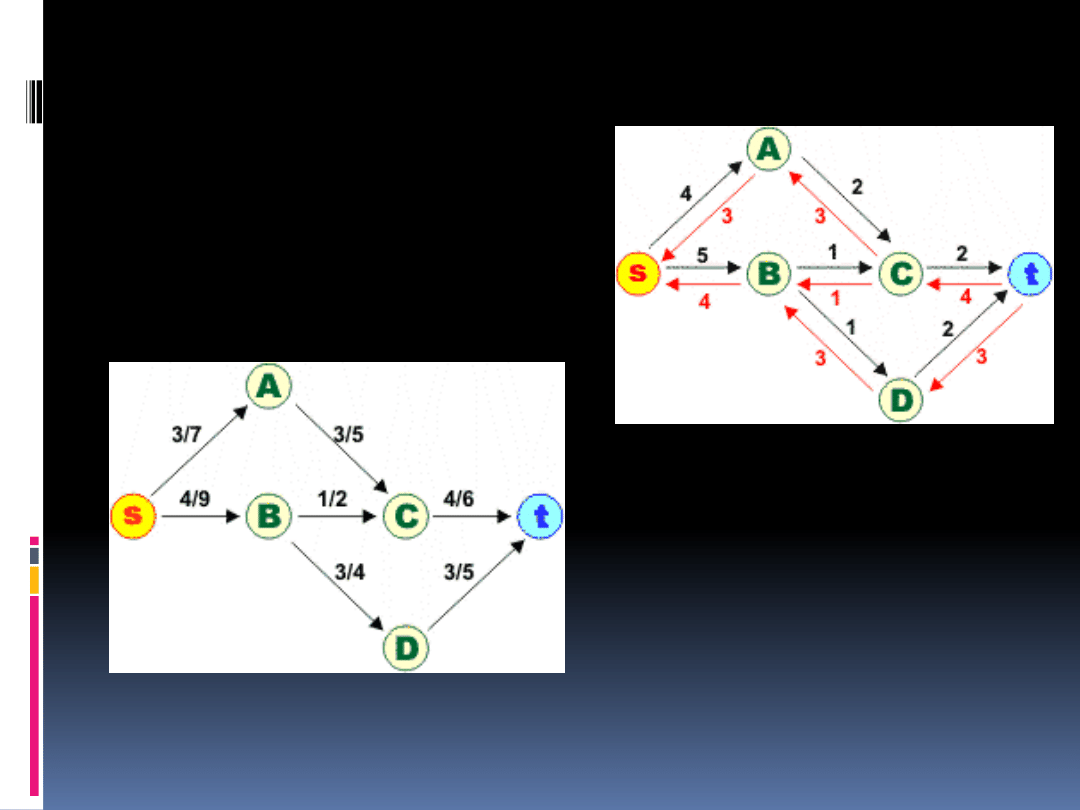
Sieć residualna

Ścieżka rozszerzająca

Ścieżka rozszerzająca jest ścieżką w sieci
residualnej (to ważne - w pierwotnej sieci takiej
ścieżki może nie być!!!) łączącą źródło s z
ujściem t. Wszystkie kanały leżące na ścieżce
rozszerzającej muszą posiadać niezerowe
przepustowości residualne. Przepustowość
residualna ścieżki rozszerzającej jest równa
najmniejszej przepustowości residualnej
kanałów należących do tej ścieżki. Fakt ten
zapisujemy następująco:
c

(p) = min{c

(u,v) | (u,v) ∈p}

Przekrój

Przekrój rozdzielający x od y jest to
zbiór krawędzi, których usunięcie
pozostawia sieć nie mającą
nietrywialnych przepływów z x do y.
Przepustowość przekroju jest sumą
przepustowości wszystkich krawędzi
należących do przekroju.