Mechanika
Mechanika
kwantowa
klasyczna
relatywistyczna
Mechanika kwantowa
Mechanika klasyczna lub
Mechanika
nie opisuje trajektorii
newtonowska –
relatywistyczna lub
mikrocząsteczek, a
mechanika wyprowadzona
einsteinowska –
jedynie
z zasad dynamiki
mechanika oparta
prawdopodobieństwo
Newtona; poprawnie
na szczególnej teorii
znalezienia się
opisuje zjawiska, jeżeli
względności;
cząstki w różnych
prędkości ciał są bardzo
prędkości ciał są
punktach przestrzeni
małe w porównaniu
porównywalne z c ≈
z c ≈ 300 000 km/s
300 000 km/s
R–nie Schrödingera
R–nie Newtona
Funkcja falowa ψ
Trajektoria r=r(t)
Mechanika klasyczna:
Kinematyka – opisuje ruch ciał bez analizowania jego przyczyn Dynamika – zajmuje się warunkami i przyczynami ruchu ciał
dy def
y
∆
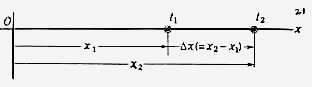
Ruch prostoliniowy wzdłuż osi X
f '(x) ≡
= lim
dx
x
∆ →0 ∆x
t
∆ = t − t
2
1
Ruch punktu materialnego
poruszającego
się w prawo wzdłuż osi X
∆x – droga przebyta w czasie ∆t Prędkość średnia:
Prędkość chwilowa:
∆x
∆
∆
∆
x
dx
v = lim =
v
=
x=x(t)
śr
t 0 ∆t
dt
t
∆
∆t 0
Przyspieszenie średnie:
Przyspieszenie chwilowe:
v
∆
∆v
dv
d2x
a
=
śr
a = lim = =
∆
v=v(t)
t
t 0 ∆t
dt
∆t 0
dt2
Druga pochodna to pochodna pierwszej pochodnej danej funkcji różniczkowanie
różniczkowanie
f(x) f’(x) f”(x)
2
dv
d dx
d x
a =
=
=
2
dt
dt dt
dt
Ruch prostoliniowy jednostajny: v=const Z definicji prędkości chwilowej:
dx
dx
v =
⇒ dx = vdt
∑ → ∫
{
dt
∆x
dx – nieskończenie mała droga
t
t
∆x – skończony kawałek drogi przebyty w czasie od
∆x = ∫ dx =∫ vdt
chwili początkowej 0 sek. do chwili t sek.
0
0
t
t
v= const
x
∆ = ∫ vdt = v∫ dt = vt t = vt − v⋅0 ⇒ x − x = vt 0
0
0
0
droga x:
x = x + vt
0
b
prędkość v:
v = const
∫f(x d
) x = F(b) − F(a)
dv
a
a =
= 0 bo v = const
W
n +
dt
x 1
zo
przyspieszenie a:
a = 0
∫ xndx =
ry
n + 1
x0+1
Z definicji prędkości chwilowej otrzymujemy, poprzez
∫dx =∫ x0dx =
= x
0 + 1
całkowanie, wzór na drogę x w ruchu jednostajnym
Ruch prostoliniowy jednostajnie zmienny: a=const b
∫f(x d
) x = F(b) − F(a)
t
t
a
Z definicji mamy:
= dv
a
⇒ dv = adt ⇒ ∆v = ∫ dv = ∫ adt W
n +
x 1
zo
dt
∫ xndx =
ry
0
0
n + 1
przyspieszenie a:
a = const
x0+1
∫dx =∫ x0dx =
= x
0 + 1
t
t
x1+1
x2
t
1
∫
=∫
=
=
a= const
∆v = ∫ adt = a∫ dt = at = at − a⋅0 = at xdx
x dx
0
1 + 1
2
0
0
∆v = v − v ⇒ v − v = at prędkość v:
=
+
0
0
v
v
at
0
t
t
dx
{
= dx
v
⇒ dx = vdt ⇒ ∆x = ∫ dx = ∫ vdt dt
0
0
∆x
t
t
t
t
t
t
t
t
1
2
∆x = ∫ vdt = ∫ (v + at d
) t = ∫ v dt + ∫ (at d
) t = v ∫ dt + a∫ tdt = v t + at
=
0
0
0
0
2
0
0
0
0
0
0
0
0
1
2
1
2
1
2
= (v t − v ⋅ 0) + ( at − a ⋅0 ) = v t + at 0
0
2
2
0
2
1
2
1
2
∆x = v t + at → x − x = v t + at 0
2
0
0
2
t2
=
+
+
droga x:
x
x
v t
a
0
0
2
Przyspieszenie w ruchu po okręgu
d
Przyspieszenie w ruchu po okręgu
ϕ
ω = dt
Równanie
x = r cos (
ϕ t)
{
parametryczne
=
ϕ
def dω
okręgu:
y
r sin (t)
α = dt
dx
dϕ
v =
= −r sin (
ϕ t)⋅
= −rωsin (
ϕ t)
x
dt
dt
dy
dϕ
v =
= r cos (
ϕ t)
= rωcos (
ϕ t)
y
r
dt
dt
ϕ
y
x
dv
dω
dϕ
a
x
=
= −r
⋅sin (
ϕ t) − rω⋅cos (
ϕ t)⋅
x
dt
dt
dt
Przyspieszenie normalne
r
r
α
a
2
= −ω r
n
= −rα ⋅sin ϕ − r 2
ω cos ϕ = v
2
− ω x
x
ω
skierowane do środka koła
dv
ω
ϕ
y
d
d
a =
= +r
⋅cos (
ϕ t) − rω⋅sin (
ϕ t)⋅
Przyspieszenie styczne
y
styczne
dt
dt
dt
r
α r
a =
v
t
α
ω
= rα ⋅cos ϕ − r 2
ω sin ϕ = v
2
− ω y
y
ω
równoległe lub antyrównoległe
do wektora prędkości v,
r
α r
r
2
zatem styczne do toru
a =
v − ω r
ω
Pochodna iloczynu dwóch lub kilku funkcji jest równa: ZO
(uv)’=u’v+uv’ gdzie u i v są dowolnymi funkcjami x RY
Stały czynnik można wynosić przed znak pochodnej: (cu)’ = cu’
dy
Pochodna funkcji złożonej: jeżeli y=f(u) i u=ϕ(x), to:
= f'(u) '
ϕ (x)
dx
x = r cos (
ϕ t)
x = r cos w i w = (
ϕ t)
x i y są złożonymi
def dϕ
ω =
y = r sin (
ϕ t)
funkcjami t
y = r sin z i z = (
ϕ t)
dt
dx
dϕ
dϕ
dϕ
v =
= (r cos w)' ⋅w' = r(cosw)' ⋅
= −r sin w ⋅
= −r
sin (
ϕ t) = −rωsin(ϕ) =
x
dt
dt
dt
dt
= −r ⋅ u
[ (t) ⋅ v(t)]
gdzie: u(t) =
(
ω t) oraz v(t) = sin (
ϕ t)
dv
du
dv
d
x
ω
d
dω
ax =
= −r
⋅ v + u ⋅
= −r
⋅sin ϕ + ω⋅
sin ϕ(t) = −r
⋅sin ϕ −
dt
dt
dt
dt
dt
dt
dϕ
dω
− rω⋅cosϕ⋅
= −r
⋅sin ϕ − rω2 cosϕ
dt
dt
dy
dϕ
dϕ
dϕ
v =
= (r sin z)' ⋅z' = r(sin z)' ⋅
= r cos z ⋅
= r
cos (
ϕ t) = rωcos (
ϕ t) =
y
dt
dt
dt
dt
= r ⋅ u
[ (t) ⋅ s(t)]
gdzie: u(t) = (
ω t) oraz (
s t) = cos (
ϕ t)
Podobnie obliczamy ay
Wyszukiwarka
Podobne podstrony:
Fizyka spr i ogólna sciaga RUCH
ściąga ruch prostoliniowy a obrotowy
ściąga ruch drogowy
Fizyka Ściąga Ruch
Inne materiały, Ściąga, REFORMACJA - ruch polityczno religijno społeczny w Europie XVI w
Fizyka ruch sciagawa
ruch - ściaga fiz, do szkoły, ściągi
Sciąga wzory(ruch płaski, energie, siły)
Ściąga z fizyk 2, Ruch jednostajny prostoliniowy
Sciągi socjologia, sciagasocjo, ZACHOWANIE-zewnętrznie obserwowalny ruch fizyczny przejawiany, wykon
TECHNOLOGIA WYTWARZANIA, Frezowanie - gotowa sciaga, Frezowanie - w procesie frezowania ruch górny w
prezentacja Ruch konsumencki
1 sciaga ppt
Wykł 05 Ruch drgający
ruch wektorowy
Ustalony ruch przez dyfuzje gazow wg Maxwella
Prezentacja klaryfikator ruch
więcej podobnych podstron