cwicz15

BARBARA SIEMEK

ZAKŁAD FIZYKI, AKADEMIA ROLNICZA

Do u ytku wewn trznego

wiczenie 15

WYZNACZANIE ZMIANY ENTROPII UKŁADU W PROCESIE

TOPNIENIA LODU

Kraków, 02.2007r.

SPIS TRE CI

TEORETYCZNA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

TERMODYNAMIKA - PODSTAWOWE POJ CIA................................................................................................. 2

STAN UKŁADU. PARAMETRY STANU ............................................................................................................... 2

CIEPLNY PRZEPŁYW ENERGII......................................................................................................................... 2

FUNKCJE STANU.............................................................................................................................................. 3

PROCESY TERMODYNAMICZNE ...................................................................................................................... 3

PIERWSZA ZASADA TERMODYNAMIKI............................................................................................................ 4

DRUGA ZASADA TERMODYNAMIKI. ENTROPIA.............................................................................................. 5

ENTROPIA W UJ CIU MIKROSKOPOWYM ....................................................................................................... 5

ENTROPIA W UJ CIU MAKROSKOPOWYM ...................................................................................................... 7

10. WYRÓWNYWANIE SI TEMPERATUR.............................................................................................................. 8

11. SPOSÓB OBLICZANIA ZMIANY ENTROPII ........................................................................................................ 9

II. CEL WICZENIA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

III.

WYKONANIE WICZENIA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

IV. OPRACOWANIE WYNIKÓW. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

V. LITERATURA UZUPEŁNIAJ CA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

VI. INDEKS. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

ZAKRES WYMAGANYCH WIADOMO CI:

Zasady termodynamiki, procesy odwracalne i nieodwracalne. Energia wewn trzna, energia

swobodna, entropia. Obowi zuje wyprowadzenie wzoru na zmian entropii w badanym procesie.

I. CZ

TEORETYCZNA

1. Termodynamika - podstawowe poj cia

Termodynamika to dział fizyki, w którym rozpatruje si procesy zachodz ce w układach

składaj cych si z du ej liczby cz stek. Układy takie zwane s układami makroskopowymi.

Poj cie układu fizycznego - wycinka materii, który został wyodr bniony w my lach z

otoczenia - jest jednym z kilku podstawowych poj stosowanych w termodynamice. W

omawianych poni ej zagadnieniach posługiwa si b dziemy poj ciami układu izolowanego,

zamkni tego i otwartego.

Układ izolowany to układ, który nie wymienia z otoczeniem ani energii ani masy. Układ

zamkni ty nie wymienia z otoczeniem masy natomiast mo e wymienia energi a układ otwarty

mo e wymienia z otoczeniem i energi i mas . Je eli badamy zachodz ce w układzie zjawiska

cieplne, to taki układ nazywamy termodynamicznym.

2. Stan układu. Parametry stanu

Opis termodynamiczny nie wymaga znajomo ci ogromnej liczby wielko ci

mikroskopowych opisuj cych układ, takich jak poło enia i pr dko ci poszczególnych atomów lub cz steczek ich energii. W celu opisu stanu układu makroskopowego posługujemy si jedynie

kilkoma wielko ciami. S nimi np. ci nienie (p), temperatura (T) lub obj to (V). Wielko ci te zwane s parametrami stanu lub parametrami makroskopowymi.

Wielko ci mikroskopowe i makroskopowe s ze sob zwi zane. Warto ci parametrów

stanu danego układu s wynikiem pewnego "u rednienia" wielko ci mikroskopowych.

3. Cieplny przepływ energii

W literaturze spotyka si dwa sposoby okre lenia „ciepła”. W pierwszej z tych definicji

poj cie "ciepła" nie wyst puje, lecz mówi si o "wymianie ciepła" lub o "cieplnym przepływie energii":

Wymiana ciepła jest sposobem przekazywania energii. Ciepło charakteryzuje wi c

pewien proces a nie układ termodynamiczny (Szczeniowski, Fizyka

do wiadczalna, T2. s.44).

W drugiej definicji poj cie "ciepła" uto samia si z pewn energi :

Ciepło to energia, która przepływa z jednego ciała do drugiego, np. w wyniku istnienia

ró nicy temperatur (Halliday D., Resnick R., Fizyka Tom 1, s.664).

Jednostk tak rozumianego "ciepła" jest 1 d ul (1J). Podobnie energi przekazan w formie cieplnego przepływu mierzymy w d ulach.

4. Funkcje stanu

Oprócz wymienionych wy ej parametrów p, V i T do opisu układu u ywa si bardziej

zło onych wielko ci fizycznych zale nych od warto ci parametrów stanu. Niektóre z nich

nazywamy funkcjami stanu. Funkcjami stanu s np. energia wewn trzna U, entalpia H, entropia S, energia swobodna F, entalpia swobodna G i inne. Zmiana warto ci funkcji stanu zale y jedynie od stanu pocz tkowego i ko cowego, a nie zale y od sposobu realizacji przej cia mi dzy tymi stanami.

Jedn z funkcji stanu jest energia wewn trzna U. Na energi wewn trzn składa si suma

energii kinetycznych ruchu post powego i obrotowego cz steczek, energii ruchu drgaj cego

cz steczek, energii potencjalnej oddziaływania cz steczek , energii chemicznej, j drowej i energii stanów elektronowych.

Dla gazu doskonałego, czyli nie oddziaływuj cych ze sob cz steczek energia wewn trzna

U jest sum energii kinetycznych tworz cych go cz steczek

U =

Ekin

Je li mamy do czynienia z okre lon ilo ci gazu doskonałego to mo na udowodni , e

zdefiniowana wy ej energia wewn trzna zale y (jest funkcj ) tylko jednego parametru stanu -

temperatury - i jest do niej proporcjonalna:

U ≈ T

5. Procesy termodynamiczne

Stan, w którym w układzie nie zachodz adne zmiany parametru stanu nazywamy stanem

równowagi termodynamicznej. Pod poj ciem procesu termodynamicznego rozumie si proces

przej cia układu z jednego stanu charakteryzowanego przez warto ci parametrów (p1, V1, T1) do innego o parametrach (p2, V2, T2). Procesy termodynamiczne mo na ilustrowa na wykresach.

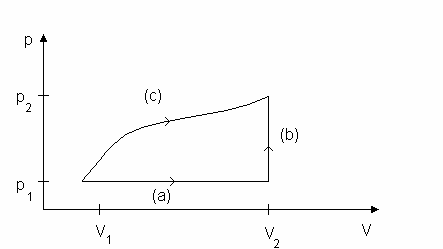
Rys. 1. Procesy termodynamiczne: (a) izobaryczny, (b) izochoryczny, (c) ze zmian ci nienia i obj to ci.

Rys.1 ilustruje trzy przykładowe procesy: pewien proces (a), w którym nie zachodzi zmiana

ci nienia (izobaryczny), proces (b) bez zmiany obj to ci (izochoryczny) oraz proces (c) ze zmian ci nienia i obj to ci

W ród procesów zachodz cych w układzie termodynamicznym mo na wyró ni procesy

odwracalne i nieodwracalne. W przyrodzie wyst puj procesy nieodwracalne, to znaczy takie, po zaj ciu których układ nie mo e samodzielnie wróci do stanu pocz tkowego, chyba e zajd

jakie zmiany w jego otoczeniu. Przykładem nieodwracalnego procesu jest upadek jakiego

przedmiotu; mo na go podnie ale nie znajdzie si on samorzutnie w poło eniu pocz tkowym.

Procesy odwracalne s u ytecznymi idealizacjami. Proces odwracalny jest to proces, w

którym układ przeszedł ze stanu pocz tkowego do stanu ko cowego, by nast pnie powróci ze

stanu ko cowego do stanu pocz tkowego przez te same stany po rednie a w jego otoczeniu nie

zaszły adne zmiany.

Nieco inn idealizacj rzeczywistych procesów s procesy quasistatyczne. Przez proces

quasistatyczny (prawie statyczny) rozumiemy proces odbywaj cy si z bardzo mał szybko ci , tak e (niesko czenie) mała zmiana warto ci parametrów, np. zewn trznego ci nienia, wystarcza do odwrócenia jego biegu.

6. Pierwsza zasada termodynamiki

Energia wewn trzna jest funkcj stanu i jej zmiana zale y jedynie od stanu ko cowego i

pocz tkowego.

Matematyczny zwi zek pomi dzy zmian energii wewn trznej ∆U przekazane na ciepło ∆Q i

prac ∆W wyra a równanie:

∆U = ∆Q + ∆W

Jest to pierwsza zasada termodynamiki, która stwierdza, i zmiana energii wewn trznej

układu mo e odbywa si poprzez wymian ciepła ∆Q oraz wykonanie pracy ∆W przez układ lub

nad układem. W szczególno ci całkowita energia wewn trzna układu izolowanego jest

wielko ci stał , niezale n od przebiegaj cych w tym układzie procesów.

7. Druga zasada termodynamiki. Entropia

Formalnie nie wszystkie procesy zgodne z pierwsz zasad termodynamiki zachodz w

przyrodzie. Obserwacje tych ogranicze doprowadziły do sformułowania drugiej zasady

termodynamiki.

Drug zasad termodynamiki sformułowa mo na w sposób nast puj cy: "wszystkie

procesy zachodz ce w przyrodzie maj charakter nieodwracalny" lub: niemo liwy jest proces, w którym ciepło przechodziłoby samorzutnie od ciał o ni szej temperaturze do ciał o temperaturze wy szej.

Ilo ciowo II zasad termodynamiki pozwala wyrazi funkcja stanu zwana entropi .

8. Entropia w uj ciu mikroskopowym

Rozwa my nast puj cy przykład. We my pod uwag cztery cz stki zamkni te w naczyniu

ponumerowane 1, 2, 3, 4, które mog znale si w stanie A lub B. Mo na wyró ni pi

mikrostanów w zale no ci od tego ile cz stek znajduje si w stanie A, a ile w B, przy czym ka dy z tych stanów mo e by zrealizowany na kilka sposobów co ilustruje tabelka

Stan

Stany mikroskopowe

Liczba

Prawdopodobie stwo

makroskopowy

mikrostanów

I A - 1 cz

1/16

B - 0 cz

II A - 3 cz

1,2,3

2,3,4 3,4,1 4,1,2

4/16

B - 1 cz

III A - 2 cz

1,2 2,3 3,4 4,1 1,3 2,4

B - 2 cz

3,4 4,1 1,2 2,3 2,4 3,1 6

6/16

IV A - 1 cz

4/16

B - 3 cz

1,2,3

2,3,4 3,4,1 4,1,2

V A - 0 cz

1/16

B - 4 cz

1 2 3 4

Jak wida w tabeli stany makroskopowe I i IV s najbardziej uporz dkowane, ka dy z

nich daje si realizowa na jeden sposób. (W = 1).

Stan III jest najbardziej nieuporz dkowany, miara nieporz dku W = 6.

Stan I i II w których w jednej cz ci naczynia byłoby wi cej cz stek ni w drugich jest najmniej prawdopodobny (ró nica ci nie doprowadziłaby do wyrównania g sto ci).

Liczba mikrostanów W realizuj cych ten sam stan makroskopowy nazywana jest

prawdopodobie stwem termodynamicznym. Jak zilustrowano na przykładzie, najbardziej

prawdopodobny (W=6) jest stan o najwi kszym „nieporz dku”. Stan jednoczesnego

przemieszczenia cz steczek do jednej połowy naczynia nazwa mo na „uporz dkowanym”.

Znalezienie wszystkich cz steczek w jednej cz ci naczynia jest mniej prawdopodobne (W=1).

Z prawdopodobie stwem termodynamicznym W zwi zana jest wielko S, zwan

entropi , która wi e si z W nast puj c definicj :

S = k ln W 1

gdzie k jest pewn stał , zwan stał Boltzmanna. Jednostk , w której wyra amy stał

Boltzmanna i entropi S jest w układzie SI [J/K].

Entropia precyzyjnie okre la stopie nieporz dku w układzie fizycznym i ułatwia

okre lenie w jakim kierunku mog zachodzi procesy w układzie izolowanym. Je eli entropia

układu w stanie pocz tkowym była równa S1 = k lnW1 a w stanie ko cowym S2 = k lnW2 to przy

przej ciu układu z tego pierwszego stanu do drugiego nast piła zmiana entropii równa:

∆S = S

(ln

)

2 − S1 = k

W2 − W1 = k • W 1

W układzie izolowanym procesy przebiegaj od stanów mniej prawdopodobnych do bardziej

prawdopodobnych, a wi c

W >

Poniewa logarytm liczby W2/W1 wi kszej od jedno ci jest dodatni, entropia w takim procesie ro nie

∆S > 0

Posługuj c si poj ciem entropii drug zasad termodynamiki mo na sformułowa nast puj co:

„w układach izolowanych mog zachodzi tylko takie procesy, w których całkowita entropia

wzrasta”.1)

9. Entropia w uj ciu makroskopowym

Doprowadzenie energii dQ do układu w formie ciepła w sposób quasistatyczny powoduje

wzrost dS entropii układu okre lony nast puj cym wyra eniem:

dS dQ

= T 3

gdzie T oznacza temperatur układu w skali Kelvina. Wzór 3 jest pewnym odpowiednikiem

definicji 1. Zbudowany jest w oparciu o poj cie parametru stanu (T)i procesu wymiany energii w formie ciepła (w ilo ci dQ). W przeciwie stwie do (1) wzór (3) definiuje jedynie zmian

(przyrost) entropii. Jest jednak wygodniejszy w zastosowaniach, poniewa temperatura i cieplny przepływ energii s stosunkowo łatwe do zmierzenia.

Do izotermicznych (T=const) procesów definicja (3) przyjmuje prost posta :

∆

S = S

2 − S

1 = T

gdzie: ∆Q - ciepło pobrane (∆Q>0) lub oddane (∆Q<0) przez układ, S1 i S2 - entropia w stanie pocz tkowym i ko cowym a ∆S - zmiana entropii. Wzór powy szy mo na zinterpretowa

nast puj co: izotermiczne dostarczenie do układu energii ∆Q w postaci ciepła powoduje wzrost nie uporz dkowania w układzie z czym wi e si wzrost entropii.

W procesach nie przebiegaj cych w stałej temperaturze zmian entropii obliczymy

równie korzystaj c z definicji (3):

∆S

= T 5

gdzie T1 - temperatura pocz tkowa układu, ™2 jego temperatura ko cowa. Obliczenie całki (5) jest mo liwe gdy znany jest przebieg zmian temperatury T zwi zany z przepływem energii dQ.

Definicja zmiany entropii (3) dotyczy procesów quasistatycznych, tzn. przebiegaj cych

przez stany bliskie stanom równowagi. Rozpatrywany w poni szym wiczeniu proces topnienia

lodu wrzuconego do kalorymetru zawieraj cego wod przebiega w sposób, który daleki jest od

spełnienia warunków quasistatyczno ci. Dla rozwi zania problemu znalezienia zmiany entropii w tym procesie wykorzystamy fakt, e entropia jest funkcj stanu. Ten sam przyrost entropii

odpowiada wi c procesowi quasistatycznemu i niequasistatycznemu o ile stany: pocz tkowy i

ko cowy w obu tych przemianach s te same. W my l tej idei proces ogrzewania wody, która

powstaje podczas topnienia lodu w zetkni ciu z wod w kalorymetrze potraktowa mo na jako

powolny proces ogrzewania wody o masie równej masie lodu i temperaturze rosn cej o 0°C do

temperatury ko cowej mieszaniny. Obliczona dla takiego procesu zmiana entropii b dzie

poprawnym rozwi zaniem postawionego zadania.

10. Wyrównywanie si temperatur

Jako przykład ustalenia kierunku, w którym proces mo e zachodzi zbadamy zmian

entropii DS dla procesu, w którym izolowany układ termodynamiczny tworz dwa podukłady o

ró nych temperaturach T1, T2, oraz T2>T1.

Dla ustalenia uwagi przyjmiemy, e układ stanowi dwie porcje wody o masach

m1=m2=100g, T1=200C, T2=400C. Z do wiadczenia wiemy, e po doprowadzeniu do kontaktu

cieplnego (zmieszaniu) temperatury obu cieczy wyrównaj si i otrzymamy ciecz o pewnej

po redniej temperaturze T. Posługuj c si zasad zachowania energii (bilansem cieplnym)

nietrudno sprawdzi , e temperatura ko cowa mieszaniny b dzie równa 300C (tzn. T=303K).

Woda o temperaturze T1=200C (293K) i o cieple wła ciwym c=4190J/kg·K ogrzewaj c si o

100C pochłania ciepło

Q = cm ∆

4190 01

. 10 4190

1 T =

•

• =

Zwi ksza przy tym swoj entropi o ∆S1

∆S

303

= 4190 • 01.• ln

=14 0

. 6

cm dT

293

Woda o temperaturze T2=400C (313K) oddaj c t sam ilo ciepła Q ochładza si o 100C.

Towarzyszy temu zmniejszenie entropii o ∆S2

∆S

303

= 4190 • 01.• ln

= 1

− 3 6

. 1

313

Całkowita zmiana entropii układu izolowanego

∆S = ∆S

1 + ∆S2

jest dodatnia i równa 14.06-13.61=+0.46J/kg. Ten wynik potwierdza przypuszczenie, e mamy do czynienia z procesem nieodwracalnym.

Dlaczego nie zachodzi proces wymiany ciepła w kierunku przeciwnym? Zasada

zachowania energii dopuszcza mo liwo takiego procesu o ile ciepło oddane Q jest równe ciepłu pobranemu. Załó my, e tak jak w powy szym przykładzie mamy do czynienia z wod o masie

m1=m2=0.1kg a przekaz ciepła Q=4190J nast puje w kierunku przeciwnym ni poprzednio.

Ró nica temperatur pomi dzy porcjami cieczy wi c wzrasta z 200C do 400C. Obliczaj c

całkowit zmian entropii w tym procesie przekonamy si , e jest ona ujemna i równa

∆S = ∆S

14 5

. 5 131

. 8

. 7 /

1 + ∆S2 = −

= −

J kg

Utwierdza to nas w przekonaniu, e proces taki jest nieprawdopodobny.

Stosuj c prawo wzrostu entropii nietrudno dowie , e w dowolnym izolowanym układzie

dwu ciał o ró nych temperaturach nie jest mo liwy samorzutny proces prowadz cy do wzrostu

ró nicy temperatur pomi dzy tymi ciałami. Wymiana ciepła musi prowadzi do wyrównania

temperatur.

11. Sposób obliczania zmiany entropii

Przedmiotem wiczenia jest wyznaczenie zmiany entropii izolowanego układu

termodynamicznego zło onego z lodu, wody i kalorymetru. Kalorymetr realizuje ide izolacji

układu od otoczenia. Zmiana entropii zwi zana jest z procesem topnienia lodu i procesami

wyrównywania si temperatur wody i kalorymetru. Do obliczenia warto ci liczbowej zmiany

entropii konieczny jest kilkakrotny pomiar temperatur i mas.

Całkowita zmiana entropii ∆S rozpatrywanego układu równa jest sumie zmian entropii: w

samym tylko procesie topnienia lodu (∆S1), podczas ogrzewania wody powstałej ze stopionego

lodu (∆S2) i podczas obni ania temperatury kalorymetru wraz z zawart w nim wod (∆S3)

∆S = ∆S1 + ∆S2 + ∆S3 6

Poszczególne przyczynki ∆S1, ∆S2 i ∆S3 s nast puj ce.

Zmiana entropii ∆S1 w procesie topnienia lodu, który zachodzi w stałej temperaturze T0=273K, jest równa:

∆S

gdzie Q - ciepło potrzebne do stopienia lodu. Poniewa Q = mL, (m oznacza mas lodu a L -

ciepło topnienia lodu) zmiana entropii ∆S1 jest równa

∆S

Zmiana entropii ∆S2 podczas ogrzewania wody powstałej ze stopionego lodu:

∆S = c

gdzie cw - ciepło wła ciwe wody, Tk - temperatura ko cowa układu, T0 - temperatura pocz tkowa równa temperaturze topnienia lodu.

Zmian entropii ∆S3 podczas obni ania temperatury wody i kalorymetru od temperatury

pocz tkowej Tp do temperatury ko cowej Tk, wspólnej dla całego układu, mo na obliczy

podobnie jak w poprzednim przypadku otrzymuj c:

∆S = (

) ln

wmw

ck mk

gdzie: mw - masa wody znajduj cej si w kalorymetrze przed stopieniem lodu, ck - ciepło

wła ciwe kalorymetru a mk jego masa.

Omówiony powy ej proces jest nieodwracalny, wi c entropia układu ro nie (∆S>O),

mimo e zmiana entropii ∆S3 jest ujemna.

II. CEL WICZENIA

Celem wiczenia jest wyznaczenie zmiany entropii układu termodynamicznego zło onego

z lodu, wody i kalorymetru towarzysz cej procesowi topnienia lodu i wyrównywania temperatur wody i kalorymetru.

III. WYKONANIE WICZENIA

1. Po dokładnym wysuszeniu wewn trznego naczynia kalorymetrycznego wyznaczy jego mas mk wraz z mieszadełkiem.

2. Napełni wewn trzne naczynie kalorymetru do połowy wod i wyznaczy mas cało ci m1.

Masa wody mw=m1-mk.

3. Umie ci naczynie z wod w osłonie termicznej kalorymetru i zmierzy temperatur

pocz tkow tp. Temperatura w skali Kelvina Tp=tp+273.

4. Osuszy bibułk kawałek lodu i wrzuci go do wody w kalorymetrze. Odczyta najni sz temperatur ko cow tk po stopieniu lodu. W skali Kelvina: Tk=tk+273.

5. Wyznaczy mas m2 kalorymetru z wod i stopionym lodem. Masa wrzuconego lodu

m = m2 - m1.

IV. OPRACOWANIE WYNIKÓW

Korzystaj c z równa (6)-(9) obliczy :

1. Zmian entropii ∆S1 w procesie topnienia lodu (ciepło topnienia lodu L=3.3·105 J/kg).

2. Zmian entropii ∆S2 wody powstałej ze stopionego lodu (ciepło wła ciwe wody

cw=4190 J/kg·K, temperatura topnienia lodu To=273K).

3. Zmian entropii kalorymetru z wod ∆S3.

4. Całkowit zmian entropii układu ∆S.

5. Oszacowa maksymalne warto ci bł dów wielko ci mierzonych bezpo rednio: mas i

temperatur (patrz "").

6. Obliczy bł d bezwzgl dny i wzgl dny całkowitej zmiany entropii ∆S. Bł d pomiaru

∆S1 mo na obliczy metod logarytmiczn a bł d ∆S2 i ∆S3 metod ró niczki zupełnej

("Obliczanie i prezentacja wyników pomiarów").

V. LITERATURA UZUPEŁNIAJ CA

Davies P., Strzałka czasu. Problemy n.4, kwiecie 1988, s.50-53

Chyla K., Fizyka dla ZSZ, Wydanie trzecie, WSziP, Warszawa 1991. s.96-103

Feynman R. P., Leighton R. B., Sands M., Feynmana wykłady z fizyki, Tom I cz

2, PWN,

Warszawa 1974

Gabrylewski E., Fizyka dla I klasy liceów ogólnokształc cych, techników i liceów zawodowych.

Wyd.VII. PZWS, Warszawa 1973, s.143-149

Halliday D., Resnick R., Fizyka Tom 1, PWN, Warszawa 1975, s.739-767

Hawking S.W., Krótka historia czasu. Strzałka czasu, PWN?, Warszawa 1990, s.135-143

Orear J., Fizyka Tom 1, WNT, Warszawa 1993, s.234-240

Piech T., Fizyka dla II klasy liceum ogólnokształc cego, technikum i liceum zawodowego.

Wyd.V. PZWS, Warszawa 1973, s.43-62

Pilawski A., Podstawy biofizyki, PZWL, Warszawa 1985, s.95-104

Reif F., Fizyka statystyczna, PWN, Warszawa 1973

Szczeniowski S., Fizyka Do wiadczalna, Tom II, PWN, Warszawa 1976, s.155-201

Zalewski K., Wykłady z termodynamiki fenomenologicznej i statystycznej, PWN, Warszawa

1978, s.49-99

VI. INDEKS

bilans cieplny (6)

ciepło (3)

energia wewn trzna (3)

funkcje stanu (3)

gaz doskonały (3)

parametry makroskopowe (2)

parametry stanu (2)

proces

izobaryczny (4)

izochoryczny (4)

procesy

nieodwracalne (4)

odwracalne (4)

quasistatycze (5)

termodynamiczne (4)

równowaga termodynamiczna (4)

termodynamika (2)

układ

izolowany (2)

makroskopowy (2)

otwarty (2)

termodynamiczny (2)

zamkni ty (2)

układ fizyczny (2)

wielko ci mikroskopowe (2)

wymiana ciepła (2)