ZADANIA DOMOWE - tekst IN_zaoczne

mechanika #

3.5. Znale!" czas przelotu samolotu mi#dzy dwoma punktami

odleg$ymi od siebie o L, je%eli pr#dko&" samolotu wzgl#dem powietrza

wynosi v , a pr#dko&" przeciwnego wiatru skierowanego pod k'tem !

1

wzgl#dem kierunku ruchu samolotu wynosi v

2.

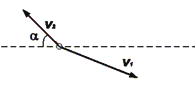
3.7. Na jakiej wysoko&ci wektor pr#dko&ci cia$a wyrzuconego z pr#dko&ci' pocz'tkow' v pod 0

k'tem ! do poziomu, utworzy k't " ((>)) ? Nie uwzgl#dnia" oporu powietrza. Napisa"

kinematyczne równania ruchu cia$a.

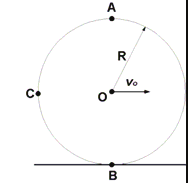
3.15. Obr#cz o promieniu R toczy si# bez po&lizgu po prostej. Pr#dko&"

&rodka O obr#czy jest sta$a i wynosi v . Oblicz warto&ci oraz wska%

0

kierunki i zwroty chwilowych pr#dko&ci i przyspiesze* tych punktów

tarcz, które w rozwa%anej chwili znajduj' si# w punktach oznaczonych

literami A, B i C.

3.19. Ko$o obraca si# wokó$ swojej osi. Znale!" jego przyspieszenie

k'towe je%eli wiadomo, %e po up$ywie czasu t od rozpocz#cia ruchu jednostajnie przyspieszonego,

wektor ca$kowitego przyspieszenia punktu po$o%onego na obwodzie tworzy k't ( z kierunkiem

pr#dko&ci liniowej tego punktu.

#

mechanika # #

5.1.7. Oblicz wysoko&", na jak' mo%e wjecha" samochód, który maj'c pocz'tkow' pr#dko&" 72

0

km/h, porusza si# w gór# z wy$'czonym silnikiem. Nachylenie zbocza wynosi 30 , a efektywny wspó$czynnik tarcia 0,1.

5.1.9. Dwa ci#%arki o masach m i m po$'czono

1

2

niewa%k' i nierozci'gliw' nici' przerzucon' przez

bloczek znajduj'cy si# na szczycie równi (rys. 5.1.9.).

mm

2 2

Wspó$czynnik tarcia mi#dzy ci#%arkiem m i równi'

2

wynosi f , a k't nachylenia równi (. Mas# bloczka

2

m1

(

mo%na pomin'". Wyznacz si$# napi#cia nici i przyspie-

szenie ci#%arków, przyjmuj'c, %e ci#%arek m porusza

1

si# w dó$.

5.1.10 Klocek o masie m = 3 kg po$o%ono na wózek o masie M = 15 kg. Wspó$czynnik tarcia mi#dzy tymi cia$ami wynosi f = 0,2. Na klocek dzia$a pozioma si$a F = 20 N, a wózek mo%e

porusza" si# swobodnie (bez tarcia) po szynach. Znajd! przyspieszenie klocka wzgl#dem

wózka.

5.1.14. Dany jest uk$ad jak na rysunku, przy czym: m1 + m2 + m3..

Tarcie i wp$yw kr'%ka pomijamy. Które z tych cia$ mo%na

zamieni" miejscami, aby si$a N napinaj'ca ni" $'cz'c' masy

m

nie uleg$a zmianie ?

1 i m2

# #

mechanika # # #

5.1.3. Winda mo%e porusza" si# w gór# i w dó$ z przyspieszeniem o takiej samej warto&ci. W

windzie tej na wadze spr#%ynowej stoi studentka. Ró%nica wskaza* wagi przy ruchu w gór# i

w dó$ wynosi 50 N. Jakie jest przyspieszenie windy, je%eli ci#%ar studentki wynosi 500 N?

5.1.4. W wagonie poruszaj'cym si# poziomo z pewnym przyspieszeniem wisi na nici

0

ci#%arek o masie 100 g. Ni" odchylona jest od pionu o k't 15 . Oblicz przyspieszenie wagonu i si$# napinaj'c' ni".

5.2.2. Ma$y ci#%arek o masie m = 100 g przywi'zano do nici o d$ugo&ci l = 50 cm i wprawiono w 0

ruch obrotowy po okr#gu w p$aszczy!nie poziomej. Ni" odchyla si# od pionu o k't ( = 45 .

Wyznacz pr#dko&" k'tow' ci#%arka, okres obiegu i si$# napi#cia nici.

5.2.5. Okres obiegu Ksi#%yca wokó$ Ziemi wynosi T = 27,32 dób ziemskich, a jego &rednia

-11

odleg$o&" od Ziemi r = 384 400 km. Oblicz mas# Ziemi. Sta$a grawitacji G = 6,67 x 10

2

2

Nm /kg .

# # #

mechanika # # # #

6.2. Kulka o masie m = 20 g wyrzucona pionowo w gór# z pr#dko&ci' vo = 200 m/s, spad$a na ziemi# z pr#dko&ci' v = 50 m/s. Obliczy" prac# si$ tarcia w powietrzu.

6.5. Na szczycie g$adkiej kuli o promieniu R po$o%ono monet#, której nadano pr#dko&"

pocz'tkow' w kierunku poziomym o warto&ci vq. W którym miejscu, licz'c od wierzcho$ka

kuli, moneta oderwie si# od niej (moneta zsuwa si# bez tarcia)? Przyspieszenie ziemskie jest

równe g.

6.18*. Na pod$odze le%y lina o masie m i d$ugo&ci l. Jeden z jej ko*ców podnosimy do góry dopóki lina nie oderwie si# od pod$ogi. Wyznaczy" minimaln' warto&" pracy jak' nale%y

wykona", aby podnie&" lin# z pod$ogi w polu grawitacyjnym Ziemi w przypadku, gdy:

a) lina jest jednorodna

b) lina jest niejednorodna i jej masa m zale%y od odleg$o&ci x od jednego z jej ko*ców 2

& x #

wed$ug wzoru m( x) ' m $ ! , gdzie x jest d$ugo&ci' podnoszonej cz#&ci sznura.

0 % l "

6.20. Cz$owiek o masie m1 = 60 kg, biegn'cy z pr#dko&ci' v1 = 8 km/h, dogania wózek o masie m2 = 90 kg, który jedzie z pr#dko&ci' v2 = 4 km/h i wskakuje na ten wózek. Z jak'

pr#dko&ci' b#dzie porusza$ si# wózek z cz$owiekiem? Jaka b#dzie pr#dko&" wózka z

cz$owiekiem w przypadku, gdy cz$owiek b#dzie bieg$ naprzeciwko wózka?

# # # #

ciep!o #

3

7

11.2. Butla gazowa o obj#to&ci V =0,3m wytrzymuje ci&nienie p =10 Pa. Znajduje si# w niej 1

kr

0

m=3369g azotu o temperaturze t =27 C. Obliczy" ci&nienie gazu w temperaturze t . Je&li w 1

1

wyniku po%aru butla ogrzeje si#, to w jakiej temperaturze nast'pi jej rozerwanie? Masa molowa

azotu: , =28g.

p

6

11.3. W procesie izobarycznym n=2mole wodoru o temperaturze T =300K i ci&nieniu p =10 Pa, 1

1

zmniejszy$o swoj' obj#to&" k=2 razy. Oblicz temperatur# ko*cow', prac# i ciep$o wyst#puj'ce w tym procesie. Przedstaw prac# na wykresie p(V).

11.7. W wyniku szybkiego rozpr#%eniu n=2 moli tlenu jego obj#to&" wzros$a s=4 razy. Obliczy"

6

przyrost energii wewn#trznej tego gazu je&li jego ci&nienie pocz'tkowe wynosi$o p =8,31x10 Pa a 1

temperatura T =300K.

1

11.10 . Mas# m = 160 g tlenu ogrzewa si# od t = 50°C do t = 60°C. Obliczy" ilo&" pobranego 1

2

ciep$a i zmian# energii wewn#trznej tlenu w przypadku, gdy ogrzewanie zachodzi$o:

a) izochorycznie,

b) izobarycznie.

#

ciep!o # #

10.5. Na jakiej wysoko&ci ci&nienie powietrza spada do po$owy swej warto&ci przy powierzchni morza? Za$o%y", %e przyspieszenie ziemskie i temperatura powietrza nie zale%' od wysoko&ci.

2

0

Dane: g=9.81m/s , t =10 C, ci&nienie p =1000hPa.

p

0

11.11. Dwa identyczne naczynia po$'czone s' zaworem. W jednym z nich znajduje si# azot pod

5

ci&nieniem p =2,64x10 Pa i w temperaturze t = 27°C a w drugim panuje pró%nia. Znale!"

1

1

ko*cow' temperatur# i ci&nienie gazu, je%eli po otwarciu zaworu cz#&" gazu przesz$a do pustego naczynia i ci&nienia w obu naczyniach wyrówna$y si#. Proces przej&cia azotu z jednego naczynia

do drugiego jest procesem adiabatycznym.

-4

2

13.2. Wspó$czynnik dyfuzji tlenu w warunkach normalnych jest równy 1,41 10 m /s. Znale!"

o

wspó$czynnik dyfuzji tego gazu w temperaturze 50 C, je%eli gaz ogrzewano przy sta$ej obj#to&ci.

-2

13.3. Wspó$czynnik przewodnictwa cieplnego gazu trójatomowego jest równy 1,45 10

-5

2

W/m K, a wspó$czynnik dyfuzji w tych samych warunkach wynosi 10 m /s. Znale!" liczb#

3

cz'steczek gazu w 1m w tych warunkach.

# #

elektrodynamika #

14.2. Dwie niewielkie, przewodz'ce kulki o jednakowych rozmiarach i ci#%arach: G = 0,05 N

zawieszono na równych niciach o d$ugo&ciach: l = 10 cm tak, %e powierzchnie styka$y si#. Jakim

$adunkiem q nale%y na$adowa" kulki aby napr#%enie nici N wynosi$o 0,1 N?

c

14.31. Metalow' kul# o promieniu R na$adowano $adunkiem q. (a) Oblicz i wykre&l zale%no&"

potencja$u i nat#%enia pola elektrycznego w funkcji odleg$o&ci od &rodka kuli. (b) Jak zmieni si#

rozk$ad pola elektrycznego, gdy zamiast metalowej, u%yjemy kuli z dielektryka na$adowanej

powierzchniowo $adunkiem q.

14.32. Niesko*czenie d$ug' prost' ni" znajduj'c' si# w pró%ni na$adowano ze sta$' g#sto&ci'

-6

liniow' $adunku - = 2 10 C/m. (a) Wyznacz modu$ nat#%enia pola E i potencja$ V jako funkcj#

odleg$o&ci r od nici. (b) Oblicz E i V dla r = 10m.

14.33. .adunki o przeciwnych znakach s' roz$o%one ze sta$ymi g#sto&ciami powierzchniowymi

+/ i –/ odpowiednio na dwóch metalowych p$aszczyznach niesko*czonych, równoleg$ych

wzgl#dem siebie i odleg$ych o d. (a) Oblicz i wykre&l zale%no&" potencja$u i nat#%enia pola

elektrycznego w funkcji odleg$o&ci mi#dzy p$ytami. (b) Jak zmieni si# rozk$ad pola, gdy jedn' z

p$yt po$'czymy z ziemi'?

#

elektrodynamika # #

A

C

16.2. Wyznaczy" indukcj# pola magnetycznego wyt-

(

worzonego przez pr'd o nat#%eniu i p$yn'cy przez

i

niesko*czenie d$ugi przewodnik zgi#ty pod k'tem

prostym: a) w punkcie A le%'cym w p$aszczy!nie

przewodnika odleg$ym od jego ko*ca o odleg$o&" h,

na przed$u%eniu jednego z ramion przewodnika (rys)

b) W punkcie C odleg$ym o h od osi przewodnika,

le%'cy pod k'tem ( do osi jednego z ramion przewodnika.

l, N

16.4. Wyznaczy" warto&" indukcji pola magnetycznego

I

wewn'trz niesko*czonego solenoidu, w którym na l jego

d$ugo&ci przypada N ciasno u$o%onych zwojów w których

p$ynie pr'd I.

B

16.7. Elektron porusza si# w jednorodnym polu magnetycznym

o indukcji B po linii &rubowej o promieniu R i skoku h,

wyznaczy" warto&" pr#dko&ci elektronu.

R

16.10. Wzd$u% osi cienko&ciennej rury biegnie prostoliniowy

h

przewód. Pr'd I p$yn'cy w rurze wraca przewodem do !ród$a.

Wyznaczy" wielko&" indukcji pola magnetycznego jako funkcj#

odleg$o&ci od &rodka rury.

# #

procesy falowe #

8.3. Cz'stka wykonuje drgania harmoniczne. W odleg$o&ciach x i x od po$o%enia równowagi jej

1

2

pr#dko&ci wynosz' v i v . Znale!" amplitud# i cz#sto&" drga* cz'stki.

1

2

8.26. W pewnym o&rodku wzd$u% osi y przemieszcza si# monochromatyczna harmoniczna fala p$aska o d$ugo&ci -. Znale!" ró%nic# faz drga* cz'stek o&rodka znajduj'cych si# na równoleg$ych p$aszczyznach A i B odleg$ych od siebie o 0y. P$aszczyzny te s' prostopad$e do osi y.

8.29. W zamocowanej na ko*cach strunie o d$ugo&ci b = 120 cm wytworzono fal# stoj'c'. W

punktach odleg$ych od siebie o d = 15 cm i d = 5 cm amplituda tej fali jest równa A = 3,5 mm.

1

2

1

Znale!" maksymaln' amplitud# tej fali. Której harmonicznej odpowiada ta fala?

8.30. W o&rodku o g#sto&ci 1 wytworzono mechaniczn' pod$u%n' fal# stoj'c'. Wychylenie cz'steczek o&rodka opisane jest równaniem: s = 2s cos(kx)cos(2t). Obliczy" &redni' g#sto&"

0

energii kinetycznej i &redni' g#sto&" energii potencjalnej ruchu falowego w w#z$ach i w strza$kach.

#

procesy falowe # #

18.5. Wi'zka promieniowania lasera o d$ugo&ci -=653 nm pada prostopadle na zapisan'

standartow' p$yt# CD. Po odbiciu na ekranie ustawionym w odleg$o&ci L=1,2m zaobserwowano

rz'd plamek. Odleg$o&" mi#dzy centraln' plamk' i s'siednimi wynosi x=0,5m.

Oblicz odleg$o&" mi#dzy &cie%kami zapisu.

18.6.

Wi'zka promieniowania lasera o d$ugo&ci -=653 nm pada prostopadle na jedwabn' tkanin#. Na

ekranie ustawionym w odleg$o&ci L=1,5m zaobserwowano sie" kwadratow' plamek Cztery

najbli%sze plamki tworz' kwadrat o boku x=3mm. Oblicz odleg$o&ci mi#dzy nitkami.

18.8.

Siatk# dyfrakcyjn' o m = 500 rys/mm o&wietlono &wiat$em o d$ugo&ci fali - = 546 nm. W jakiej

odleg$o&ci od siebie znajduj' si# maksima pierwszego oraz drugiego rz#du na ekranie odleg$ym o

L = 0,5 m od szczelin?

18.11.

Obserwator znajduje si# w odleg$o&ci L = 10 m od punktowego !ród$o &wiat$a o mocy

promieniowania P = 100 W. Obliczy" maksymalne warto&ci nat#%enia pola elektrycznego i

magnetycznego w miejscu, w którym stoi obserwator. Za$o%y", %e !ród$o jest monochromatyczne

i promieniuje w sposób jednorodny we wszystkich kierunkach

# #