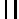3.5m
α
130 kN
V
β
A
HB
VB
Obliczenie reakcji:
RA = VB = HB = 130 kN
Równania sił przekrojowych: 0 < α < 180°
M(α) = RA 3.5 (1 - cosα)
Q(α) = RA sinα
N(α) = - RA cosα
0 < β < 90°
M(β) = VB 3.5 (sinβ - cosβ +1) Q(β) = -VB cosβ - HB sinβ
N(β) = VB sinβ - HB cosβ
Obliczenia zapisujemy w tabelce: α M kNm Q kN N kN
0
0.0
0.0 -130.0
45
133.3
91.9
-91.9
90
455.0 130.0
0.0
135
776.7
91.9
91.9
180
910
0.0 130.0
β
M
Q
N
0
0.0 -130.0 -130.0
45
455.0 -183.8
0.0
90
910.0 -130.0 130.0
Wykresy:
130
91.92
91.92
91.92
455
133.3
91.92
776.7
130
910
M
Q
130
N
130
183.8
455
130
130
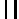
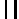
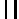
A. Zaborski, Łuk
Łuk paraboliczny
45 kN/m
y
15 kN/m
1.5 m
α
x
HA
HB
VA
VB
3 m
3 m
Obliczenie reakcji:
HA = HB = 52.5 kN, VA = 26.25 kN, VB = 63.75 kN
Równanie łuku:
y(x) = a x2 + b x +c, z warunakami: y(0) = 0, y(3) = 1.5 m, y(6) = 0, sk d: y(x) = -1/6 x2 + x
pochodna:
y’(x) = 1 – x/3 = tgα
Równania sił przekrojowych: 0 < x < 3 m
M(x) = 26.25 x – 52.5 y
Q(x) = 26.25 cosα - 52.5 sinα
N(x) = -26.25 sinα - 52.5 cosα
3 m < x < 6 m
M(x) = 26.25 x – 52.5 y – 45/2 (x – 3)2 + 30/3 1/6 (x – 3)3
Q(x) = 26.25 cosα - 52.5 sinα - 45 (x – 3) |cosα| + 30/3 ½ (x –3)2 |cosα|
N(x) = -26.25 sinα - 52.5 cosα - 45 (x – 3) |sinα| + 30/3 ½ (x –3)2 |sinα|
Obliczenia prowadzimy w tabelce: x [m] y [m]
α
cosα
sinα
M
Q
N
0 0.000
0.7854
0.7071
0.7071
0.00 -18.56 -18.56
1 0.833
0.5880
0.8321
0.5547 -17.50
-7.28 -29.12
2 1.333
0.3218
0.9487
0.3162 -17.50
8.30 -41.50
3 1.500
0.0000
1.0000
0.0000
0.00 26.25 -52.50
4 1.333 -0.3218
0.9487 -0.3162 14.17
3.56 -54.15
5 0.833 -0.5880
0.8322 -0.5547 10.83
-7.28 -67.95
6 0.000 -0.7854
0.7071 -0.7071
0.00
-7.95 -82.20
Sprawdzenie, czy pochodna momentu zginaj cego po współrz dnej zwi zanej z osi pr ta jest równa sile poprzecznej, np. w pierwszym przedziale: dM( s)
dM( x) d x
=
= 26.25 cos α − 52.5 tg α cos α = 26.25 cos α − 52.5sin α = Q( s) d s
d x
d s
17.5
17.5
M
14.17 10.83
41.5
52.5
ekstremum M
29.12
54.15 67.95
26.25
18.56
N
82.2
8.301
3.56
7.28
Q
7.28
7.95
18.56
A. Zaborski, Łuk Przykład osi racjonalnej łuku parabolicznego q
f
HA
HA
N
RA
l
Okre lamy równanie osi łuku w postaci paraboli 2. stopnia o strzałce równej f i rozpi to ci l oraz obliczamy reakcje jak dla układu 3-przegubowego: 4 f
2
y = −
−
=
=
.
2 ( x 2
lx)
ql
ql
, R
, H
l
A
A
2
8 f
Równanie momentów zginaj cych ma posta : 2
2
qx
ql
ql
4
2
f
qx
M ( x) = R x A − H y
A
−
=
x −
−
( 2 x − lx − = = .
2
)
0
2
2
8 f
l
2
Je li moment zginaj cy jest to samo ciowo równy zero, to i siła poprzeczna musi by to samo ciowo równa zero i łuk pracuje jedynie na ciskanie. Łuk o takiej osi nazywamy łukiem o osi racjonalnej.
Wyszukiwarka
Podobne podstrony:
105 Łuk swobodnie podparty obciążony prostopadle do swojej płaszczyzny
łuk kołowy
Łuk kołowy
Łuk odruchowy, Biologia
Łuk Konstantyna Wielkiego
28 Test „bolesny łuk”, test Lift off, test Yergasona, test “pustej puszki” – wykonanie i
Test luk
Kae Sa Luk, czyli o jedzeniu oczami
101 Łuk trójprzegubowy
łuk wypukly
1 Luk elektryczny (1)
luk poprawa(k)
łuk wklęsly
kretschmer lewinski luk
luk poz pdiu2
luk karakamby zawistowska P65AEI7KRRODA2NAPF76TT73PW6WJ2JOP6UN3GA
łuk triumfalny
Test luk
ŁUK TYTUSA
György Lukács Powstawanie i wartość utworów literackich [1923]
więcej podobnych podstron