Rozchodzenie się fal dźwiękowych
Aby mogła w danym ośrodku (np. powietrzu) mogła powstać fala dźwiękowa musi w nim istnieć jakieś źródło fal, np poruszać się jakiś obiekt, który zapoczątkuje zburzenia. JeŜeli ruch tego obiektu jest dostatecznie szybki, to powoduje spręŜanie powietrza. Gdy w pewnym miejscu gęstość cząsteczek jest większa niŜ w sąsiednim, cząsteczki poruszają się z obszaru o większej gęstości do obszaru o mniejszej gęstości, aŜ do wyrównania ciśnień. Aby mogła powstać fala dźwiękowa cząsteczki wybiegając z obszaru o większej gęstości i ciśnieniu muszą przekazywać pęd cząsteczkom znajdującym się w obszarze o mniejszej gęstości. Jest to moŜliwe jeŜeli odstęp między grzbietem i doliną ciśnienia jest znacznie większy od średniej drogi swobodnej cząsteczek, czyli od odległości jaką przebywają cząsteczki zanim zderzą się z innymi cząsteczkami.
Aby moŜliwie uprościć rozwaŜania będziemy zajmowali się falami w jednym wymiarze.
Opisujemy ruch powietrza przy pomocy funkcji χ (x,t) określającej przemieszczenie środka masy małego obszaru gazu ale nie dotyczącej zachowania pojedynczych cząsteczek.
Zjawiska fizyczne zachodzące w czasie propagacji fali dźwiękowej:
∆ χ
1. Ruch gazu wywołuje zmianę gęstości: ∆ ρ = − ρ
0 ∆ x
∂ χ
lub d ρ = − ρ
0 ∂ x
2. Zmianie gęstości odpowiada zmiana ciśnienia: ∆ P = Κ∆ ρ
∂2χ
P
∂
3. Nierównomierny rozkład ciśnienia wywołuje ruch gazu: ρ0
= −
t
∂ 2
x
∂
P
∂
∂
∂
=
( P + P
∆ ) =
( P
∆ )
0
x
∂
x
∂
x
∂
Po podstawieniu (1) do (2) a potem do (3) otrzymujemy:
2
2
∂ χ
∂
∂χ
∂ χ
ρ
= −
− K ⋅ ρ
= ρ Κ
0
0
0
2
2
t
∂
x
∂
x
∂
x
∂
2
2
∂ χ
∂
=
χ
Κ
Κ
dP
=
∂
gdzie
t 2
∂ x 2
d ρ
po podstawieniu K=v2 otrzymuje się równanie ruchu falowego dla fal dźwiękowych rozchodzących się w powietrzu:
2
2
∂ χ
1 ∂
=
χ
∂ x 2
v 2 ∂ t 2
gdzie χ opisuje przemieszczanie środka masy pewnego małego obszaru z jego normalnego połoŜenia równowagi. Takie samo równanie opisuje teŜ zmiany ciśnienia oraz zmiany gęstości gazu. Rozwiązaniem równania falowego jest dowolna, dwukrotnie róŜniczkowalna funkcja argumentu (x-vt)
13/ 1
χ = f ( x − vt ) lub χ = g (ω t − kx ) gdzie k=ω /v
2
2
2
2
∂ χ
∂ χ
∂ χ
1 ∂ χ
W trzech wymiarach równanie falowe ma postać:
+
+
=
2
2
∂ x
∂ y
∂ z 2
v 2 ∂ t 2
χ = g(ω t − kx)
O rozwiązaniu
gdzie k jest wektorem falowym ( kx, ky, kz) o kierunku i zwrocie zgodnym z kierunkiem i zwrotem propagacji fali i o wartości danej równaniem
1
2
2
2
ω
k = ( k + k + k
2
=
x
y
z )
gdzie
v
Zjawisko Dopplera
Efektem typowym dla ruchu falowego jest efekt Dopplera. Zjawisko to polega na zaleŜności częstości fal odbieranych przez odbiornik od prędkości źródła fal i odbiornika względem ośrodka w którym rozchodzi się fala. RozwaŜmy to zjawisko na przykładzie fal dźwiękowych. Niech dla uproszczenia źródło i obserwator poruszają się po tej samej prostej.
MoŜliwe są cztery przypadki:
• Gdy obserwator zbliŜa się od źródła:
JeŜeli
obserwator
porusza
się
w
stronę
nieruchomego źródła napotyka fale o nie
zmienionej długości.
λ = const.
które względem niego rozchodzą się z prędkością:
v' = c + v0 gdzie c-prędkość dźwięku
v′
c + v 0
Obserwowana częstość f’ wynosi więc: f ′ =
=
λ
λ
c
Podstawiając: λ =
f
c + v 0
′ =
otrzymujemy: f
f
c
• Gdy obserwator oddala się od źródła v’ = c – v, a obserwowana częstość wynosi c − v
f ′ = f
0
c
13/ 2

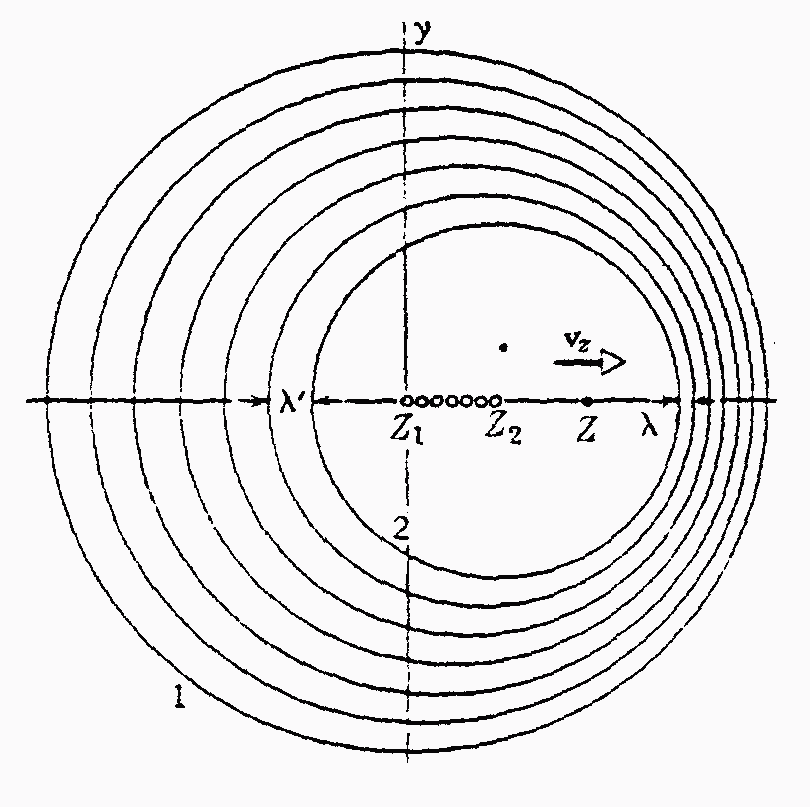
• Gdy źródło dźwięku się porusza to zmianie ulega długość fali a jej prędkość względem nieruchomego obserwatora pozostaje stała. JeŜeli źródło porusza się w kierunku obserwatora to kolejne fronty falowe wysyłane są z coraz mniejszej odległości. Zatem długość fal się zmniejsza.
λ ′ = λ − s z
v
s
= v T
z
=
z
z
f
v
c
c
v
z
λ ′ = λ −
z
=
−
f
f '
f
f
c
f ′ = f c − vz
c
•
′ =
Gdy źródło oddala się od obserwatora λ ' = λ + s
f
f
z i wówczas
c + v
z
Ogólnie
c + v cos
0
θ
f ′ = f
0
c + v cos θ
z
z
gdzie θ0 i θz są to kąty utworzone przez wektory prędkości odbiornika v0 i prędkości źródła vz z wektorem R łączącym odbiornik i źródło fal.
Elementy akustyki fizjologicznej
Słyszalne fale dźwiękowe są to fale o częstotliwościach od 16 do 20000 Hz. Fale te działają na organy słuchu człowieka powodując wraŜenia słuchowe. Fale o częstotliwościach f ≤ 16
Hz nazywają się infradźwiękami lub poddźwiękami. Fale o częstotliwościach f ≥ 2·10-4 Hz nazywają się ultradźwiękami lub naddźwiękami.
Charakter wraŜeń słuchowych zaleŜy od widma częstotliwości dźwięku. Szumy mają ciągłe widmo częstotliwości z jakiegoś przedziału. Dźwięki muzyczne mają dyskretne widmo częstotliwości: f, 2f, 3f ...
Sinusoidalna fala dźwiękowa nazywa się tonem, wysokość tonu zaleŜy od jego częstości, im większa częstość tym wyŜszy ton. Ton podstawowy złoŜonego dźwięku muzycznego to ton odpowiadający najmniejszej częstości f0. Barwa dźwięku zaleŜy od tonów harmonicznych o częstościach 2f0, 3f0, ... występujących razem z tonem podstawowym.
Miarą wielkości wraŜeń słuchowych jest poziom głośności. Poziom głośności zaleŜy od częstości i ciśnienia akustycznego, jest on wielkością subiektywną, zaleŜną od indywidualnych moŜliwości percepcji ucha ludzkiego. WyraŜa się go w skali decybelowej w odniesieniu do poziomu progu słyszalności
p
p0 – próg słyszalności
L
2 k lg
e
=
k = 1 daje wynik w belach [B]
p
k = 10 daje wynik w decybelach [dB]
0
13/ 3