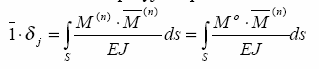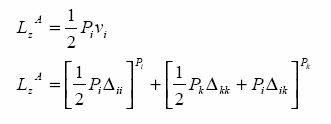
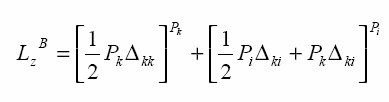
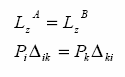
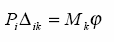
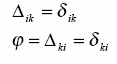
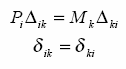
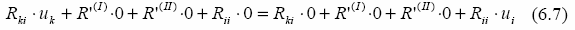
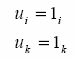
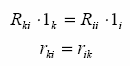
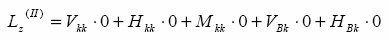
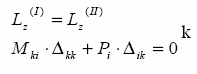
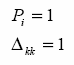
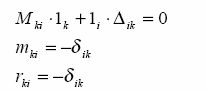
TWIERDZENIE BETTIEGO (o wzajemności prac)
TWIERDZENIE MAXWELLA (o wzajemności przemieszczeń)
TWIERDZENIE RAYLEIGHA (o wzajemności reakcji)
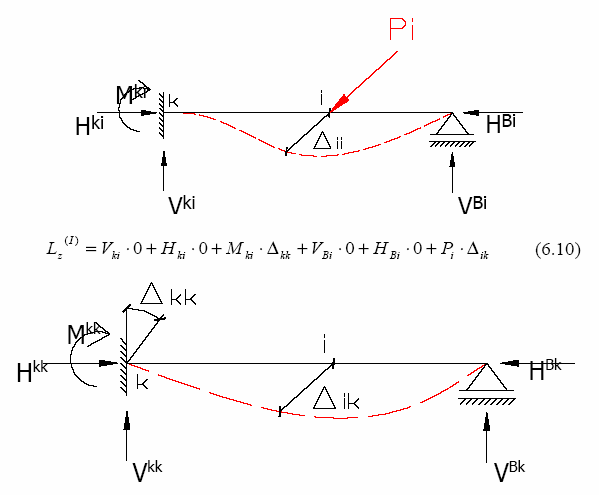
Niech na dowolny układ ramowy statycznie wyznaczalny lub
Rozpatrzmy dowolny układ statycznie wyznaczalny lub
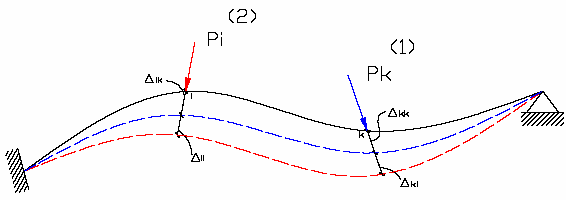
Ciało odkształcalne przedstawione na rysunku:
niewyznaczalny, ale o
niewyznaczalny. ZałóŜmy
niepodatnych podporach i przy braku napręŜeń termicznych,
obciąŜenia:
działa układ sił i
Pierwszy typ obciąŜenia: Niech na układ działa siła
momentów skupionych. ObciąŜenia te rozdzielić moŜna, w
jednostkowa Pk=1, skierowana w
sposób dowolny, na dwie
kierunku przesunięcia δki. Drugi typ obciąŜenia: Na układ grupy, z których jedną nazwiemy układem sił Pi a drugą
działa siła jednostkowa
układem sił Pk (przez „siły”
Pi=1, skierowana w kierunku przesunięcia δik.
rozumieć naleŜy zarówno siły uogólnione).
ZałóŜmy, Ŝe podpory nie osiadają, a temperatura nie zmienia
Sytuacja pierwsza A: Najpierw przykładamy siłę Pi, a
się, tak Ŝe mamy do
następnie siłę Pk.
czynienia wyłącznie z napręŜeniami wywołanymi obciąŜeniem
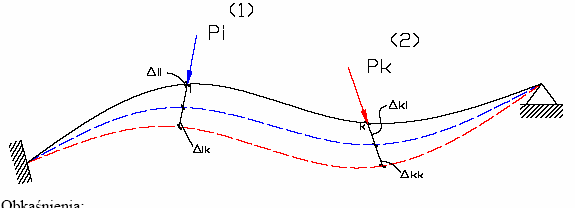
Obkaśnienia:
zewnętrznym. Między
Punkt i - zestaw punktów poddany obserwacjom,
przesunięciami δik i δki zachodzi szczególny związek.
Pi - układ sił (moment, siła skupiona itd.) działających na
Przykłąd 1:
punkt i,
∆jn - przemieszczenie punktu j wywołane przyczyną w pkt n,
Zakładamy
ogólny
przypadek
konstrukcji
statycznie
∆jn - przemieszczenie punktu j wywołane jednostkową
niewyznaczalnej. Przypuśćmy
przyczyną w pkt n,
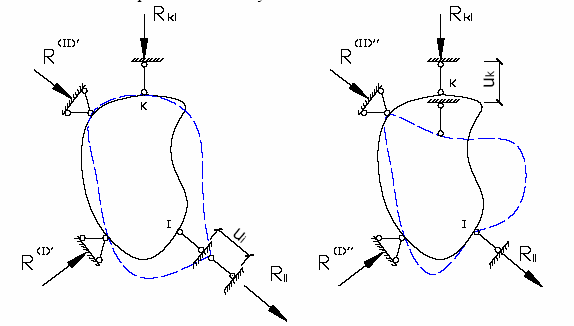
wymuszenie kinematyczne ui po kierunku podpory „i” (rys 1).
Następnie załoŜymy
wymuszenie kinematyczne uk po kierunku podpory k (rys 2).
Przemieszczenia podpór
przyjmijmy za jednostkowe. Zgodnie z twierdzeniem Bettiego moŜna
zapisać pracę
pierwszego układu :
Przemieszczenia moŜna przyjąć jako jednostowe:
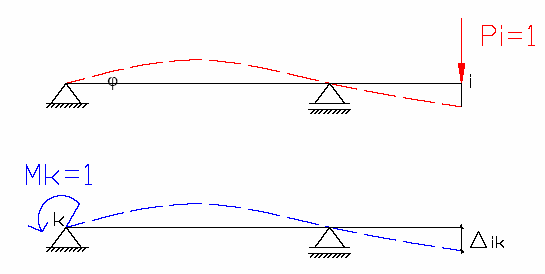
Do danej belki przykładamy jednostkowe obciąŜenia; w punkcie
„i” jednostkową siłę
Pi=1 a w punkcie „k” jednostkowy moment Mk=1. korzystając z
Obkaśnienia:
wyŜej przedstawionego
twierdzenia Bettiego moŜna zapisać zaleŜność:
Punkt i - zestaw punktów poddany obserwacjom,
Pi - układ sił (moment, siła skupiona itd.) działających na
Podstawiając przyjęte przemieszczenia do wzoru (6.7) otrzymamy:
punkt i,
∆jn - przemieszczenie punktu j wywołane przyczyną w pkt n,
∆jn - przemieszczenie punktu j wywołane jednostkową
przyczyną w pkt n,
Warto zauwaŜyć, Ŝe kąt obrotu na którym pracuje moment to
nic innego jak ∆ki.
Najpierw przykładamy grupę sił Pi a następnie do tego stanu
Przyjmując, Ŝe układy sił obciąŜających są jednostkowe,
wprowadzamy grupę sił Pk.
przemieszczenia zapisujemy
Zgodnie z przyjętą konwencją reakcje od jednostkowych
Praca sił zewnętrznych w sytuacji A:
następująco:
przemieszczeń zapisujemy
małą literą podobnie jak przemieszczenia od jednostkowych reakcji.
Twierdzenie:
Reakcja uogólniona rik odpowiadająca i-temu przemieszczeniu
uogólnionemu a wywołana jednostkowym przemieszczeniem uk=1
k-tego
Wykorzystując powyŜsze załoŜenia otrzymamy:
więzu, równa jest uogólnionej reakcji rki odpowiadającej u-temu
przemieszczeniu uogólnionemu w wywołanej jednostkowym
przemieszczeniem ui i-tego więzu.
TWIERDZENIE O WZAJEMNOŚCI PRZEMIESZCZEŃ REAKCJI
Niech na dowolny układ ramowy statycznie wyznaczalny lub
Sytuacja druga B: Najpierw przykładamy siłę Pk, a następnie
niewyznaczalny, przy
siłę Pi
braku napręŜeń termicznych, działa najpierw układ sił Pi. Zapiszemy
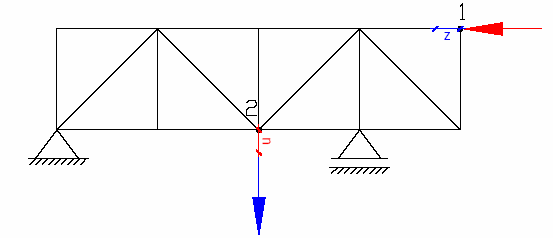
Przykład 2:
pracę tego układu
Do kratownicy przyłoŜono siłę jednostkową w puncie 1, która
jako L(z)1. Następnie załóŜmy podatność jednej podpór np. kąta
wywołała
obrotu i zapiszmy jego
przemieszczenie w punkcie 2. Następnie do tej samej
pracę jako L(z)2.
kratownicy przyłoŜono siłę
jednostkową w puncie 2, która wywołała przemieszczenie
punktu 1. Zgodnie z
powyŜszym twierdzeniem przemieszczenia punktu 1 i 2 są
sobie równe.
Siły przykładamy podobnie jak w poprzednim wypadku z tą
róŜnicą, Ŝe najpierw
przykładamy grupę sił Pk, a następnie do tego stanu
wprowadzamy grupę sił Pi. Praca sił
zewnętrznych od sytuacji B:
Twierdzenie:
Przemieszczenie uogólnione δik odpowiadające i-tej sile
linia A=linia B
uogólnionej i
Zgodnie z zasadą superpozycji oraz faktem, Ŝe wartość pracy
wywołane działaniem jednostkowej siły uogólnionej Pk=1 jest
Zgodnie z zasadą superpozycji oraz faktem, Ŝe wartość pracy nie
nie zaleŜy od historii
równe
zaleŜy od kolejności
(kolejności działania przyczyn) obciąŜeń moŜna zapisać:
przemieszczeniu δki odpowiadającemu k-tej sile uogólnionej i
działań przyczyn praca jednego układu i drugiego są sobie równe:
wywołanemu działaniem jednostkowej siły uogólnionej Pi.
Przyjmujemy, Ŝe siła i przemieszczenie są jednostkowe:
Twierdzenie:
JeŜeli na ustrój spręŜysty działają dwa niezaleŜne układy
obciąŜeń, spełniające
równania równowagi to: układ sił Pi wykonuje na
przemieszczeniach
wywołanych układem sił Pk taką samą pracę jak siły Pk na
Wykorzystując zaleŜności (6.11) i (6.12) otrzymujemy:
przemieszczeniach
spowodowanych układem sił Pi.
Twierdzenie:
JeŜeli na ustrój spręŜysty w punkcie i działa układ sił Pi=1 wywołuje
w
punkcie k reacje i niezaleŜnie od tego jeśli uogólnione
przemieszczenie
∆k podpory k-tej towarzyszy pojawienie się w punkcie i
przemieszczenia
δik to rzut reakcji rki na kierunek przemieszczenia ∆ik jest równy rzutowi
przemieszczenia ∆ik na kierunek uogólnionej siły Pi z przeciwnym
znakiem.
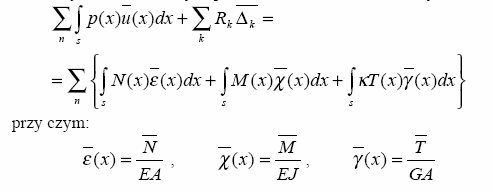
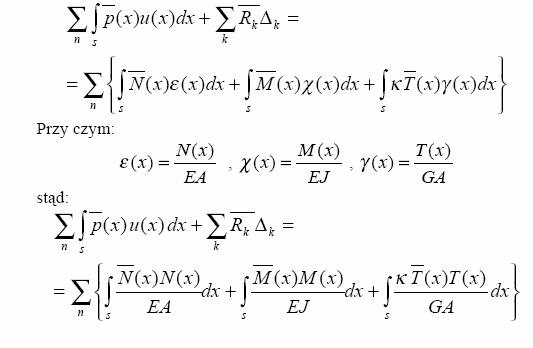
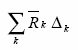
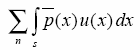
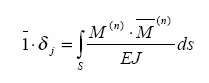
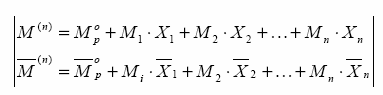
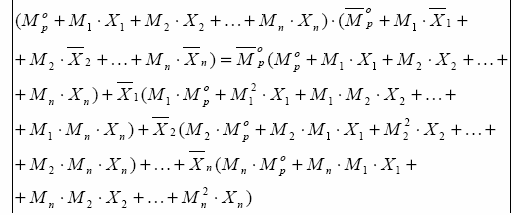
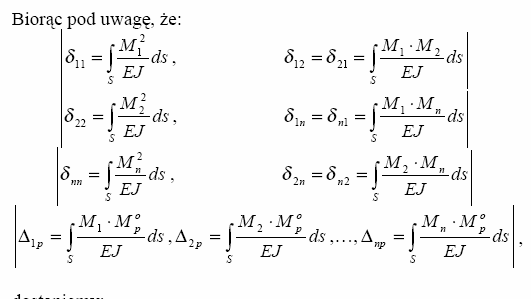
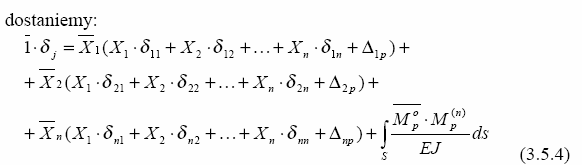
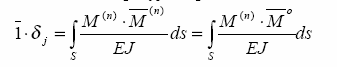
RÓWNANIE PRACY WIRTUALNEJ
2.2. Interpretacja
Pierwsze twierdzenie redukcyjne
1.1. Twierdzenie
Dotychczas korzystaliśmy z twierdzenia, Ŝe siły zewnętrzne
W celu obliczenia dowolnego przemieszczenia w układzie
JeŜeli na układ działa obciąŜenie rzeczywiste spełniające
wykonywały
statycznie
(warunki równowagi),
pracę na wirtualnych przemieszczeniach. Teraz zróbmy
niewyznaczalnym, wystarczy rozwiązać układ ten od obciąŜenia
to obciąŜenie zewnętrzne wykonuje na przemieszczeniu
odwrotnie tzn. stwórzmy
rzeczywistego, zaś wirtualny stan obciąŜeń określić dla dowolnego
wirtualnym pracę
rzeczywisty model układu (Rys.2.2.1.), a następnie obciąŜmy go
układu podstawowego statycznie wyznaczalnego.
równą pracy uogólnionych sił przekrojowych na wirtualnych
siłami wirtualnymi
Dowód tego twierdzenia jest następujący (przytoczymy go
odkształceniach
(pomyślanymi)
(Rys.2.2.2.)
i
obliczmy
rzeczywiste
uwzględniając
(na wirtualnych przemieszczeniach wewnętrznych).
przemieszczenia naszego
w
obliczeniach
przemieszczeń
jedynie
wpływ
momentów
1.2. Interpretacja
układu prętowego. Musimy przy tym zaznaczyć, Ŝe wirtualne
zginających):
Przyjmujemy dowolny układ pozostający w równowadze
obciąŜenie spełnia
warunki statycznej dopuszczalności, jest niezaleŜne od
obciąŜeń
zewnętrznych rzeczywistych i czasu, a zarazem jest
obciąŜeniem stosunkowo
małym oraz ciągłym (przynajmniej raz róŜniczkowalnym).
Zgodnie z zasadą superpozycji mamy:
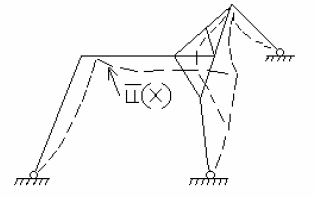
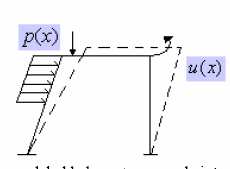
Rys.1.2.1. Rzeczywisty model układu prętowego, obciąŜony
rzeczywistymi siłami
p( x) pod wpływem, których doznaje przemieszczeń
Iloczyn w wyraŜeniu podcałkowym (dla uproszczenia zapisu
pominięto
mianownik EJ) moŜemy przedstawić jako:
Rys. 2.2.1. Rzeczywisty model układu prętowego, obciąŜony
rzeczywistymi siłami
p( x) pod wpływem, których doznaje przemieszczeń
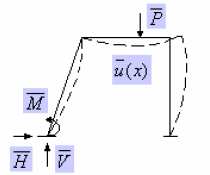
Rys.1.2.2.
Ten
sam
układ
ale
z
wymuszonym
przemieszczeniem wirtualnym ) ( x u
(kinematycznie dopuszczalnym)
Rys. 2.2.2. Ten sam układ, ale obciąŜony siłą wirtualną ) ( x P
pod wpływem, której
doznaje przemieszczeń wirtualnym ) ( x u
z L - praca wszystkich rzeczywistych sił czynnych
obciąŜających układ oraz
biernych pracujących na przemieszczeniach wirtualnych
(wymuszonych
kinematycznie)
W L - praca wszystkich sił wewnętrznych rzeczywistych na
L - praca sił wirtualnych pracujących na rzeczywistych
odkształceniach
przemieszczeniach
wirtualnych
(na
wirtualnych
przemieszczeniach
(tzn. wytworzonych przez rzeczywiste obciąŜenia zewnętrzne)
wewnętrznych)
W L - praca wszystkich wirtualnych sił wewnętrznych
pracujących na rzeczywistych
odkształceniach
2.1. Twierdzenie 2
JeŜeli na układ działa dowolne zewnętrzne obciąŜenie
wirtualne,
spełniające warunki równowagi to wykonuje ono pracę na
rzeczywistych
przemieszczeniach
(wywołanych
przez
rzeczywiste
obciąŜenie zewnętrzne)
równą pracy wirtualnych sił przekrojowych na rzeczywistych
gdzie:
odkształceniach
(na rzeczywistych przemieszczeniach wewnętrznych).
- całkowita praca wirtualnych sił biernych
(reakcji) na
przemieszczeniach (osiadaniach) rzeczywistych
Na mocy równań kanonicznych metody sił, wartości w nawiasach są
równe zeru.
Ostatecznie twierdzenie to przyjmie postać:
-
całkowita
praca
wirtualnych obciąŜeń na rzeczywistych
przemieszczeniach
N(x) - funkcja sił normalnych wywołana od obciąŜenia
zewnętrznego
(rzeczywistego)
N(x) - funkcja sił normalnych wywołana od obciąŜenia
Uogólnienie relacji (3.5.5) na przypadek, w którym uwzględnia się wirtualnego
wpływ
T(x) - funkcja sił poprzecznych wywołana od obciąŜenia
wszystkich przyczyn na przemieszczenia nie nastręcza Ŝadnych
zewnętrznego (rzeczywistego)
trudności.
T(x) - funkcja sił poprzecznych wywołana od obciąŜenia
wirtualnego
M(x)
-
funkcja
momentów
wywołana
od
obciąŜenia
zewnętrznego
(rzeczywistego)
M(x) - funkcja momentów wywołana od obciąŜenia wirtualnego
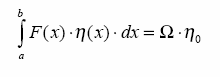
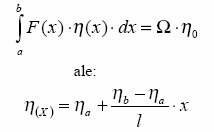
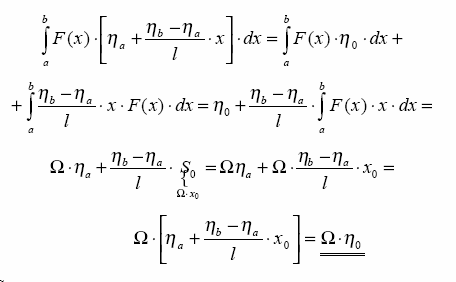
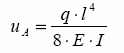
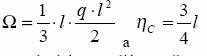
Drugie twierdzenie redukcyjne
W celu obliczenia dowolnego przemieszczenia w układzie
statycznie
niewyznaczalnym, wystarczy rozwiązać układ ten od obciąŜenia
wirtualnego, zaś rzeczywisty stan obciąŜeń określić dla dowolnego
układu podstawowego statycznie wyznaczalnego.
Dowód tego twierdzenia jest analogiczny jak przy twierdzeniu
pierwszym
z tym, Ŝe w grupowaniu wyraŜeń przed nawiasami występują
czynniki
Xk.
Ostatecznie twierdzenie to przyjmie postać:
Warto zaznaczyć, Ŝe sprawdzeń kinematycznych jest bardzo
duŜo, gdyŜ
moŜemy
przyjąć
wiele
róŜnych
układów
podstawowych.
Reasumując,
kontrole kinematyczną najlepiej przeprowadzać na innym układzie
podstawowym niŜ przy liczeniu niewiadomych, poniewaŜ efektem
tego
sprawdzenia
byłoby
wykazanie
poprawności
równania
kanonicznego.
SPOSÓB WERESZCZEGINA-MOHRA OBLICZANIA CAŁEK
ZauwaŜmy, Ŝe w równaniu (1.16) występują całki z iloczynu dwóch
funkcji
(np. M M p). W przypadku, gdy obie są ciągłe, a jedna z nich jest liniowa w
określonym przedziale, to całkę z ich iloczynu moŜna obliczyć w
prosty sposób,
korzystając z wykresów tych funkcji.
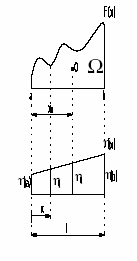
Słuszne jest twierdzenie:
Jeśli w pewnym przedziale określone są dwie róŜne funkcje
ciągłe, z których co najmniej jedna jest liniowa, to całka z ich iloczynu równa jest iloczynowi pola wykresu funkcji krzywoliniowej
przez rzędną wykresu liniowego występującą pod środkiem
cięŜkości wykresu krzywoliniowego. Niech F(x) jest funkcją krzywoliniową, zaś (x) liniową. Wówczas:
Dowód: zgodnie z tw.(2.1) moŜemy zapisać:
stąd po podstawieniu do wzoru (2.2) otrzymujemy:
So - to moment statyczny pola Ωwzględem punkty 0.
Wróćmy do przykładu z wcześniejszego wykładu, gdzie
obliczaliśmy
przemieszczenie pionowe punktu A belki jak na poniŜszym
rysunku (rys.2.2a).
Otrzymaliśmy, Ŝe uA (przemieszczenie) wynosi:
MoŜna je wyznaczyć w znacznie prostszy
sposób!
Wykreślmy wykresy momentów dla naszej
belki przy obciąŜeniu równym q (rys.2.2a)oraz przy
obciąŜeniu siłą wirtualną równą 1(rys.2.2b). JeŜeli
Cto rzędna funkcji liniowej odpowiadająca
połoŜeniu środka cięŜkości C pola wykresu
gdzie:
Otrzymany wynik jest identyczny z wynikiem całkowania.