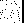Fala pada prostopadle z próżni (długość fali λ ) do ośrodka o o
względnej przenikalności elektrycznej ε w4 = 16 przez dwie ćwierćfalowe warstwy pośredniczące o względnych przenikalnościach elektrycznych ε w2, ε w3, 1 < ε w2 < ε w3 < 16.
Wiedząc, że ε
oraz grubość tej warstwy
w3 = 8, dobrać ε w2
d 2
tak, aby w próżni nie było fali odbitej.
Narysować względny rozkład amplitud fal E( z) i H( z).
ośrodek 1
ośrodek 2
ośrodek 3
ośrodek 4
ε =1
ε = ?
1
w
w 2
ε = 8
ε =16
w 3
w 4
z
– d
– d
0
23=– d 2– d 3
3
K 06
1
ZADANIE 1 (2)
• Fala rozchodzi się w kierunku +0z
• Struktura: ośrodek 1: próżnia dla z < - d przy czym 23
d 23 = d 2 + d 3
ośrodek 2: dielektryk o εw2 dla - d 23 < z < - d 3
ośrodek 3: dielektryk o εw3 dla - d 3 < z < 0
ośrodek 4: dielektryk o εw4 dla z > 0
• Dane:2π
λ
λ
π
2
0
λ =
0
Γ = Γ (− d ) = 0
d =
=
=
2
we
1
23
β
4
4 ε
2 ε β
0
w 2
w 2
0
λ
λ
λ
π
ε = 8
3
0
0
d =
=
=
=
w 3
3
4
4 ε
8 2
4 2β
w 3
0
ε =16
w 4
• Obliczyć: ε
= ?
d = ?
w 2
2
Współczynniki fazy w ośrodkach:
β = β
β = ε β
β = ε β =
β
β = ε β = 4β
1
0
2 2
2
w 2
0
w 3
w 3
0
0
4
w 4
0
0
K 06
2
1
Impedancje właściwe ośrodków:
Z
Z
Z
Z
Z
Z = Z
0
Z =
0
0
Z =
=
0
0
Z =
=
1
0
2
ε
3
ε
2 2
4
ε
4
w 2
w 3
w 4
Impedancja widziana w z = – d :
=
−
3
Z
Z ( d )
we 3
3
3
2
Z
Z + jZ tg(β d ) 0
4
3
3 3
Z
= Z
2
Z
8
Z
we 3
3 Z + jZ tg(β d ) 3
0
Z
=
=
=
we 3
3
4
3 3
π
π
Z
Z 0
2
β
4
d = 4 2β
=
3 3
0
4
4 2β
2
0
Impedancja widziana w z = – d :
=
−
23
Z
Z ( d )
we 2
2
23
2
Z 0
Z
+ jZ tg(β d )
2
we 3
2
2 2
Z
= Z
Z
ε
2 Z
2
w 2
0
we 2
2
=
=
=
Z + jZ tg(β d ) Zwe 2
2
we 3
2 2
Z
Z
ε
we 3
0
w 2
π
2
β d =
2 2
2
K 06
3
ZADANIE 1 (4)
W ośrodku 1dla z = – d : 23
Z − Z
we
0
Γ = Γ (− d ) =
= 0
⇒ Z = Z
= Z
⇒ ε = 2
we
1
23
Z + Z
we
we 2
0
w 2
we
0
λ
λ
λ
Grubość ośrodka 2 ( d
2
d =
=
=
2):
0
0
2
4
4 ε
4 2
w 2
Współczynnik odbicia w ośrodku 3 dla z = 0: Z
Z
0
0
−
Z − Z
4
2 2
2 − 2
4
3
Γ = Γ (0) =
=
=
= 3
− + 2 2 = −0.172
34
3
Z + Z
Z
Z
0
0
+
4
3
2 2
+
4
2 2
Współczynnik fali stojącej w ośrodku 3: 1
2
2
34
ρ
+ Γ
−
=
=
= 2 = 1.414
3
1− Γ
− +
34
1
2
K 06
4
2
Współczynnik odbicia w ośrodku 3 dla z = – d : 3
− j 2β
− π
3 d 3
Γ (− )
j
d = Γ e
= Γ e
= −Γ = 3− 2 2 = 0.172
3
3
34
34
34
Współczynnik odbicia w ośrodku 2 dla z = – d : 3
Z
Z
0
0
−
Z
− Z
−
we
2
2
2 2
3
2
Γ = Γ (− d ) =
=
=
= −3+ 2 2 = −0.172
23
2
3
Z
+ Z
Z
Z
0
0
+
we 3
2
2 2
+
2
2
Współczynnik fali stojącej w ośrodku 2: 1+ Γ
2 − 2
23
ρ =
=
= 2 = 1.414
2
1− Γ
− +
23
1
2
Współczynnik odbicia w ośrodku 2 dla z = – d : 23
− j 2β
− π
2 d 2
Γ (−
)
j
d
= Γ e
= Γ e
= 3− 2 2 = 0.172
2
23
23
23
K 06
5
ZADANIE 1 (6)
W ośrodków 4 dla z = 0:
E+ (0) = E
4
0
E (0)
Na granicy ośrodków 3 i 4 ( z = 0): E (0) = E
3
3
0
= 1
E 0
W ośrodku 3 dla z = 0 :
E (0) E+ (0) E− (0) E+ (0) E+ (0) E+
=
+
=
+ Γ
=
(0) 1+ Γ
= E
3
3
3
3
34
3
3
(
34 )
0
+
1
E (0) =
E
−
Γ34
E (0) =
E
3
0
1+ Γ
3
0
1+ Γ
34
34
W ośrodku 3 dla z = – d : 3
π
j
+
+
− jβ −
+
3 ( d
E
3 )
2
0
E (− d ) = E (0) e
= E (0) e = j 3
3
3
3
1+ Γ34
−
+
−Γ34
E (− d ) = Γ (− d ) E (− d ) = j E
3
3
3
3
3
3
0
1+ Γ34
+
−
1− Γ34
E (− d ) = E (− d ) + E (− d ) = j E
E (− d )
1− Γ
3
3
34
3
3
3
3
3
3
0
=
= 2
1+ Γ34
E
1+ Γ
0
34
K 06
6
3
1− Γ
Na granicy ośrodków 2 i 3 ( z = – d ): 34
−
=
−
=
3
E ( d ) E ( d ) j
E
2
3
3
3
0
1+ Γ
W ośrodku 2 dla z = – d : 34
3
E ( d ) E+ ( d ) E− ( d ) E+
−
=
−
+
−
=
(− d ) 1+ Γ
2
3
2
3
2
3
2
3 (
23 )
+
1
1
1− Γ34
E (− d ) =
E (− d ) = j
E
2
3
2
3
0
1+ Γ
1+ Γ 1+ Γ
23
23
34
−
Γ
Γ
1− Γ
23
23
34
E (− d ) =
E (− d ) = j
E
2
3
2
3
0
1+ Γ
1+ Γ 1+ Γ
23
23
34
W ośrodku 2 dla z = – d : 23
π
j
+
+
−
− Γ
jβ − d
+
1
1
2 (
2 )
2
34
E (− d ) = E (− d ) e
= E (− d ) e = −
E
2
23
2
3
2
3
0
1+ Γ 1+ Γ
23
34
E− ( d )
( d ) E+ ( d ) E+
−
= Γ −
−
= −Γ
(− d )
2
23
3
23
3
23
23
3
23
+
−
1− Γ 1− Γ
23
34
E (− d ) = E (− d ) + E (− d ) = −
E
2
23
2
23
2
23
0
1+ Γ 1+ Γ
23
34
E (− d )
1− Γ 1− Γ
2
23
23
34
=
= 2
E
1+ Γ 1+ Γ
K 06
0
23
34
7
ZADANIE 1 (9)
Na granicy ośrodków 1 i 2 ( z = – d ): 23
1− Γ 1− Γ
23
34
E (− d ) = E (− d ) = −
E
1
23
2
23
0
1+ Γ 1+ Γ
23
34
W ośrodku 1 dla z = – d :
+ −
=
−
3
E ( d ) E ( d ) 1
23
1
23
Normalizacja pola elektrycznego względem E+ (− d ): 1
23
E (− d )
E (− d )
1
23
2
23
=
= 1
E+ (− d )
E+ (− d )
1
23
1
23
E (− d )
E (− d )
1+ Γ
1
2
3
3
3
23
=
=
=
E+ (− d )
E+ (− d )
1− Γ
2
1
23
1
23
23
E (0)
E (0)
1+ Γ 1+ Γ
1
3
4
34
23
=
=
=
E+ (− d )
E+ (− d )
1− Γ 1− Γ
2
1
23
1
23
34
23
K 06
8
4
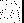

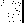







ZADANIE 1 (10)
ε =1
ε = 2 ε = 8 ε =16
1
w
w 2
w 3
w 4
f = 3 GHz
1
2
3
4
1
0.8
0.6
0.4
)| 3 0.2
-d 2
(-d
0
10
|E -0.2
E/ -0.4
-0.6
-0.8
-1
-70
-60
-50
-40
-30
-20
-10
0
10
20
z [mm]
K 06
9
5
Wyszukiwarka
Podobne podstrony:
K06 pf08L zadania rozwiazanie zad1
K06 pf08L zadania rozwiazanie zad2
K05 pf08L zadania rozwiazania
K03 pf08L zadania rozwiazania Nieznany
K04 pf08L zadania rozwiazania
K02 pf08L zadania rozwiazania
K05 pf08L zadania rozwiazania
zadania i rozwiazania z przekrojów 2
,projektowanie materiałów inżynierskich, zadania i rozwiązania Umocnienie roztworowe
Zadania z rozwiazaniami ZaiP zadanie 3
belki proste zadania z rozwiaza Nieznany (2)
Obliczanie pochodnych Zadanie Rozwiazanie zadania domowego id
ARYT ZADANIA i rozwiazania
Matematyka finansowa zadania z rozwiązaniami 2
Zadania z rozwiązaniami 1 8
Zadania z rozwiazaniami ZaiP, zadanie 1 rozwiazanie
więcej podobnych podstron