WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

POLITECHNIKI WARSZAWSKIEJ

Zakład Teorii Maszyn i Robotów

Laboratorium Podstaw Automatyki i Sterowania IV

Instrukcja do ćwiczenie nr 7A

Wyznaczanie transmitancji widmowej na podstawie danej

charakterystyki skokowej

Wstęp

Właściwości dynamiczne liniowych układów o stałych skupionych można określić m.in. na podstawie odpowiednich charakterystyk zarówno w dziedzinie czasu jak też dziedzinie częstotliwości. W pierwszym przypadku często wykorzystuje się charakterystyki impulsową i skokową natomiast w drugim, charakterystyki częstotliwościowe (np. wykresy Nyquista lub Bodego). Znajomość transmitancji operatorowej układu a co za tym idzie transmitancji widmowej pozwala na wyznaczenie obu typów charakterystyk. W związku z tym zachodzą również możliwości:

• wyznaczania transmitancji widmowej układu na podstawie charakterystyki skokowej;

• wyznaczania charakterystyki skokowej na podstawie transmitancji widmowej układu.

Celem ćwiczenia jest zapoznanie studentów z metodą wyznaczania transmitancji widmowej układu na podstawie zdjętej doświadczalnie charakterystyki skokowej.

Podstawy teoretyczne

Jeżeli znana jest charakterystyka impulsowa g( t) układu, będąca odpowiedzią na impuls Diraca δ( t), to na jej podstawie można wyznaczyć transmitancję widmową układu G( jω) =P( ω) +jQ( ω) z zależności:

∞

G( jω) = g t

( ) ⋅ e− jω t dt

∫

(7A.1)

0

Związek (7A.1) wynika z faktu, że charakterystyka impulsowa układu liniowego jest oryginałem transmitancji operatorowej tego układu.

Z uwagi na to, że w praktyce nie można ściśle zrealizować wymuszenia δ( t), często stosuje się odpowiedź skokową h( t) układu do oceny jego właściwości dynamicznych.

Charakterystyka skokowa jest łatwa w realizacji doświadczalnej a jej pochodna pierwszego rzędu względem czasu jest równa charakterystyce impulsowej:

d

g( t) =

h( t)

dla h(0) = 0

(7A.2)

dt

W związku z tym równanie (7A.1) można zapisać w postaci:

∞  d



G( jω) =

h t

( ) ⋅ e− jω t dt

∫



(7A.3)

0  dt



Jeśli charakterystyka h(t) nie jest podana w postaci analitycznej, lecz graficznej (np.

została zdjęta doświadczalnie), wtedy transmitancję widmową układu można wyznaczyć w 2

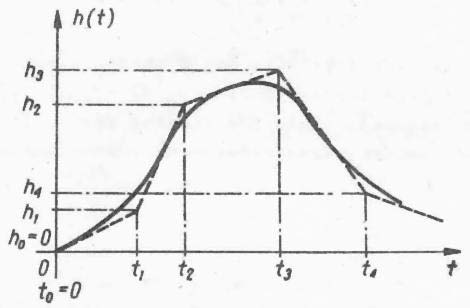
sposób uproszczony. W tym celu dokonuje się aproksymacji uzyskanej krzywej za pomocą linii łamanej (Rys. 7A.1).

Rys. 7A.1. Zasada aproksymacji charakterystyki skokowej h(t)

Przybliżoną wartość pochodnej funkcji h( t) dla każdego przedziału aproksymacji określa iloraz różnicowy w przód:

h − h

k

k 1

−

B =

;

dla k=1,2,…, n ,

(7A.4)

k

t − t

k

k 1

−

(gdzie wielkości hk i tk oznaczają współrzędne k-tego punktu załamania, natomiast n jest liczbą odcinków linii łamanej).

Zależność 7A.4 ma również zastosowanie w przypadku ćwiczenia, gdy

charakterystykę skokową rejestruje się przy użyciu przetwornika analogowo-cyfrowego (A/C). Wielkości hk i tk oznaczają wtedy współrzędne k-tego punktu pomiarowego a interwały ( tk- tk-1) są równe okresowi próbkowania przetwornika ∆ t.

Po uwzględnieniu (7A.4) wyrażenie na transmitancję widmową przyjmie postać: t

n

k

n

− ω

jB

j t

k

− jω t

− ω

G( jω) = ∑ B

e

dt =

e

e

k ∫

∑

(

k

j tk 1

−

−

)

ω

(7A.5)

k 1

=

k 1

=

tk 1

−

Po przekształceniach szukaną transmitancję widmową można zapisać w dogodnej formie do wykreślenia charakterystyki amplitudowo-fazowej (A-F):

n

1

P(ω) =

∑ B (sinω t −sinω t )

k

k

k −1

ω k=1

(7A.6)

n

1

Q(ω) =

∑ B (cosω t − cosω t )

k

k

k −1

ω k=1

3

Przebieg ćwiczenia

Ćwiczenie laboratoryjne nr 7A stanowi uzupełnienie i kontynuację ćwiczenia nr 7

„Badanie charakterystyk częstotliwościowych i przebiegów nieustalonych podstawowych członów automatyki”. Zakłada się, że studenci wykonali wcześniej ćwiczenie nr 7 i znają sposób pomiaru charakterystyk A-F czwórników RLC przy użyciu analizatora transmitancji.

Część pomiarowa ćwiczenia obejmuje:

• Pomiary (analizatorem transmitancji) charakterystyk A-F wskazanych przez asystenta czwórników;

• Zarejestrowanie odpowiedzi skokowych badanych elementów przy użyciu

przetwornika A/C (karta: PCL-812 lub PCL18) obsługiwanego przez program

SCOPE.

Rejestracja charakterystyk skokowych przy użyciu programu SCOPE:

1. Uruchomić mikrokomputer PC w trybie DOS, (Boot Partition 4);

2. Uruchomić program SCOPE z dysku C, (C:\cd scope);

3. Ustawić parametry przetwornika A/C wg wskazań asystenta;

4. Zadeklarować nazwę pliku, do którego zostanie zapisana odpowiedź na sygnał

wymuszenia (opcja File Save, przykładowa nazwa pomiar1) 5. Połączyć wejście badanego czwórnika z generatorem sygnału fali prostokątnej; 6. Połączyć wyjście badanego czwórnika z wejściem przetwornika A/C;

7. Zarejestrować przebieg odpowiedzi na sygnał wymuszenia (opcja RUN). W tym celu należy tak dobrać amplitudę i częstotliwość sygnału fali prostokątnej oraz nastawy programu SCOPE, aby uzyskany na monitorze wykres zawierał fragment

odpowiadający poszukiwanej charakterystyce skokowej.

Na rysunku 7A.2 pokazano przykładowy przebieg zarejestrowanego sygnału wyjściowego z elementu oscylacyjnego.

10

8

6

4

2

0

-2

-4

-6

Ts

-8

-100

50

100

150

200

250

300

350

400

450

500

Rys. 7A.2. Odpowiedź elementu oscylacyjnego na wymuszenie sygnałem fali prostokątnej.

4

8. Zapisać do pliku uzyskany przebieg, wciskając klawisz funkcyjny F2. Jeżeli nie zadeklarowano inaczej, to plik zostanie zapisany w katalogu C:\SCOPE (pod

wprowadzoną w pkt. 4. nazwą z dodanym automatyczne rozszerzeniem dat) 9. Skonwertować zapisany plik ( pomiar1.dat) do formatu ASCII real - opcja File Convert ascii Real. Po udanej operacji zostaje wyświetlona nazwa skonwertowanego pliku z nowym rozszerzeniem ( pomiar1.rel). Plik ten należy skopiować na dyskietkę używając komendy DOS, copy pomiary1.rel A:\

Opracowanie wyników pomiarów

Zapisana w skonwertowanym pliku odpowiedź badanego elementu na wymuszenie sygnałem fali prostokątnej zawiera nagłówek oraz kolumnę liczb odpowiadających wartościom przebiegu w równoodległych odstępach czasu ∆ t.

W przykładowym nagłówku (patrz ramka poniżej) znajdują się informacje o parametrach zarejestrowanego przebiegu i użytego przetwornika A/C. Wartość częstotliwości próbkowania fp ("SAMPLING RATE PER CHANNEL: 25KHz") określa potrzebny do obliczeń okres próbkowania ∆ t=1/ fp.

"======THIS DATA FILE IS CREATED BY PC-SCOPE ======"

"FILE NAME : INER1.REL "

"DATA FORMAT : ASCII FILE "

"CARD TYPE : PCL-812 "

"START CHANNEL : 0 "

"STOP CHANNEL : 0 "

"TOTAL CHANNELS : 1 "

"VOLTAGE RANGE : -10 V ---> +10 V "

"SAMPLING RATE PER CHANNEL : 25KHz "

"DATE : 20 DEC. 2005"

"TIME : 21:36:39.59"

"DATA"

"CH. 1"

"================================================"

W celu obliczenia poszukiwanej charakterystyki A-F należy wcześniej wyznaczyć znormalizowaną odpowiedź skokową, rozważając tylko fragment zapisanego przebiegu, ograniczonego czasem osiągnięcia wartości ustalonej Ts (Rys. 7A.2).

Kolejność postępowania:

1. Określić okres próbkowania ∆ t na podstawie nagłówka;

2. Korzystając z dowolnego edytora tekstu należy usunąć z pliku nagłówek oraz liczby z kolumny danych niedotyczące przedziału czasu T . Zapisać plik pod nową nazwą.

s

5

3. Unormować (przeskalować) przebieg w ten sposób, aby wartość ustalona h( t) była równa jeden, natomiast h(0)=0

4. Wykonać wykres unormowanej charakterystyki skokowej w celu sprawdzenia poprawności wykonania powyższych operacji;

5. Korzystając z zależności (7A.4) oraz (7A.6) obliczyć składowe transmitancji widmowej P( ω) oraz Q( ω) w zakresie pulsacji ω∈(0, 2π104); Uwaga:

Przedstawiony powyżej schemat obliczeń wymaga zautomatyzowania. W tym celu zaleca się zastosowanie programu Matlab lub MS Excel.

Sprawozdanie

Sprawozdanie powinno zawierać:

• opis przebiegu ćwiczenia;

• wyniki pomiarów i obliczeń;

• wykresy zmierzonych charakterystyk;

• porównanie na jednym rysunku dwóch charakterystyk amplitudowo-fazowych badanego elementu: zmierzonej miernikiem transmitancji oraz uzyskanej z obliczeń;

• dyskusję wpływu częstotliwości próbkowania sygnału odpowiedzi skokowej na dokładność odtworzenia charakterystyki A-F;

• wnioski.

6