27.

ZASTOSOWANIE I. ZASADY TERMODYNAMIKI DO OPISU

PRZEMIAN GAZU DOSKONAŁEGO

Gaz doskonały

Gaz doskonały — nazywany również gazem idealnym — jest to gaz spełniający następujące warunki:

1. cząsteczki gazu poruszają się chaotycznie we wszystkich kierunkach, z których żaden nie jest uprzywilejowany

2. między cząsteczkami nie działają żadne siły, poza krótką chwilą, w której następuje zderzenie

3. zderzenia cząsteczek są doskonale sprężyste

4. cząsteczki od zderzenia do zderzenia poruszają sie ruchem jednostajnym 5. suma objętości cząsteczek gazu jest dużo mniejsza niż objętość naczynia, wktórym znajduje się gaz

W fizyce klasycznej gas doskonały opisuje równanie Clapeyrona (równanie gazu doskonałego): pV = nRT

(27.1)

gdzie: p — ciśnienie gazu; V — objętość gazu; n — liczba moli; R — stała gazowa; T — temperatura.

Równanie ( 27.1) można również zapisać w postaci: pV = Nk T

B

(27.2)

gdzie: N — ilość cząsteczek gazu; kB — stała Boltzmanna.

Równanie gazu doskonałego można stosować dla gazów rzeczywistych znajdujących się pod odpowiednio małym ciśnieniem. Pewne gazy, takie jak powietrze, azot, tlen, nawet w warunkach normalnych niewiele różnią się od gazu doskonałego Pierwsza zasada termodynamiki

Zmiana energii wewnętrznej układu jest równa sumie pracy, wykonanej przez lub nad układem i ciepła dostarczonego lub oddanego przez układ.

d U = Q− W

(27.3)

gdzie: U — energia wewnętrzna układu; W — praca wykonana przez układ(znak „+”) lub nad układem(znak „–”); Q — ciepło dostarczone lub oddane przez układ Przemiany gazu doskonałego

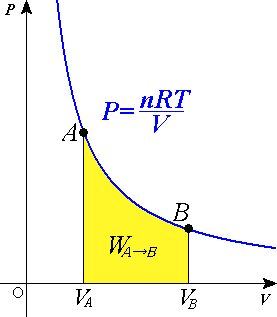
Przemiana izotermiczna ( Rys.1) jest to proces zachodzący w stałej temperaturze. Warunek T = const równoważny jest warunkowi pV = const lub pAVA = pBVB (prawo Boyle'a-Mariottte'a).

W przemianie izotermicznej zmiana energii wewnętrznej jest równa zero, gdyż temperatura gazu nie zmienia się, pierwsza zasada termodynamiki dla przemiany izotermicznej pryzmuje postać: d U =0= Q− W

(27.6)

stąd

 Q= W

(27.5)

co oznacza, że całe ciepło pobierane przez gaz jest zużywane na wykonanie pracy.

1

Pracę wykonaną przez gaz w przemianie izotermicznej obliczamy ze wzoru: V B

W =∫ p d V

(27.6)

V A

Podstawiając ciśnienie p= nRT otrzymujemy V

V B d V

V

W = nRT ∫

= nRT ln B

(27.7)

V

V

V

A

A

T= const

P= const

Rys.1 Przemiana izotermiczna

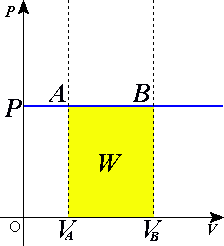
Rys. 2 Przemiana izobaryczna

Przemiana izobaryczna ( Rys. 2) jest to proces zachodzący w stałym ciśnieniu p = const.

Z równania gazu doskonałego wynika zależność V/T = const lub VA/TA=VB/TB (prawo GayLussaca) W czasie przemiany izobarycznej gaz pobiera ciepło i wykonuje i wykonuje pracę. Ilość ciepła potrzebna do ogrzania n moli gazu od temperatury T do temperatury temperatury T + d T, w przemianie izobarycznej wyraża się wzorem:

 Q= n C p dT

(28.9)

T B

Q=∫ nC d T= nC  T − T = nC  T

(27.9)

p

p

B

A

p

T A

gdzie CP — ciepło molowe przy stałym ciśnieniu.

Praca wykonana przez gaz w przemianie wyraża się wzorem: V

V

B

B

W =∫ p d V = p∫ d V = p V − V = p V

(27.10)

B

A

V

V

B

B

Pierwsza zasada termodynamiki dla przemiany izobarycznej pryzmuje postać: d U = Q− W

(27.11)

2

po scałkowaniu:

 U = nC P  T − p  V

(27.12)

Przemiana izochoryczna ( Rys. 3) jest to proces zachodzący w stałej objętości ( V = const).

Z równania gazu doskonałego otrzymujemy p/T= const lub pA/TA=pB/TB (prawo Charlesa).

W przemianie izochorycznej objętość gazu pozostaje stała, czyli nie wykonuje on pracy:

 W = p d V =0

(27.13)

Ilość ciepła potrzebna do ogrzania n moli gazu od temperatury T do temperatury T+ d T wyrażona się wzorem:

T B

Q=∫ nC d T= nC  T − T = nC  T

(27.14)

V

V

B

A

V

T A

gdzie CV — ciepło molowe przy stałym ciśnieniu.

Pierwsza zasada termodynamiki dla przemiany izochorycznej przyjmuje postać: d U = Q−0

(27.15)

po scałkowaniu otrzymujemy:

 U = n CV  T

(27.16)

W przemianie izochorycznej gaz nie wykonuje pracy, czyli całe ciepło dostarczone do gazu zużywane jest na zwiększenie energii wewnętrznej gazu.

Rys. 3 Przemiana izochoryczna

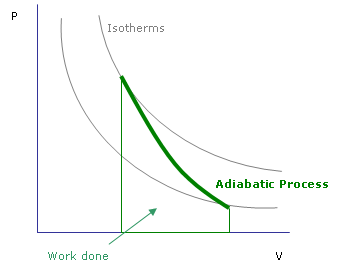
Rys. 4 Przemiana adiabatyczna

Przemiana adiabatyczna ( Rys. 4) jest to proces, podczas którego nie zachodzi wymiana ciepła z otoczeniem (  Q=0 ). Można to uzyskać poprzez oddzielenie układu od otoczenia dobrymi izolatorami cieplnymi lub jeżeli proces przeprowadzamy dostatecznie szybko.

Pierwsza zasada termodynamiki dla procesu adiabatycznego opisana jest równaniem: d U =0− W

Czyli w przemianie adiabatycznej praca wykonana przez układ równa jest ubytkowi energii wewnętrznej układu.

3