ROZCIĄGANIE PRĘTA PROSTEGO
NAPRĘŻENIA DOPUSZCZALNE
1. Analiza pręta statycznie wyznaczalnego
Przy osiowym rozciąganiu i ściskaniu w przekrojach poprzecznych pręta występu-ją tylko naprężenia normalne σ. Badania doświadczalne wykazują, że przy ściskaniu większość materiałów podlega tym samym zależnościom, co przy rozciąganiu.
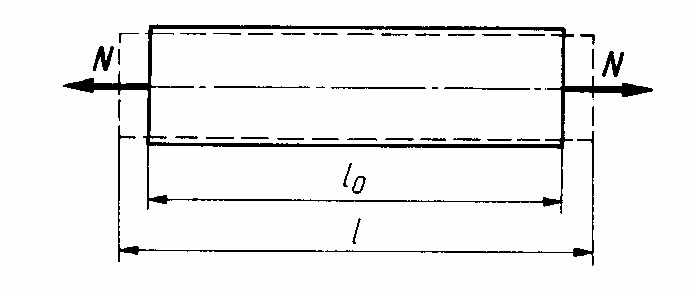
Zatem, rozpatrzymy przypadek pręta rozciąganego siłą N (rys. 1).
Rys. 1. Pręt rozciągany siłą N
Na podstawie zasady de Saint-Venanta przyjmuje się, że niezależnie od sposobu przyłożenia obciążenia w poszczególnych przekrojach poprzecznych pręta naprę-
żenia normalne są rozłożone równomiernie (σ = const). Stąd
N = ∫ σ dA = σ ∫ dA = σ A
σ = N
A
(1)
A
A
Podczas rozciągania długość początkowa pręta lo zwiększa się, a wymiary po-przeczne ulegają zmniejszeniu.
Bezwzględne wydłużenie pręta jest równe σ
∆
Nl
l =
0 =
l
EA
E 0
(2)
W celu obliczenia naprężeń i odkształceń w poszczególnych przekrojach pręta należy wyznaczyć rozkład sił wzdłużnych N. Wartość siły wzdłużnej w do-wolnym przekroju poprzecznym jest równa sumie algebraicznej rzutów na oś pręta wszystkich sił zewnętrznych po jednej stronie rozpatrywanego przekroju n
N = ∑ Pi
(3)
i=1
1
W przypadku, gdy rozpatrywany pręt składa się z kilku odcinków o różnych przekrojach, wydłużenie bezwzględne pręta oblicza się sumując algebraiczne zmiany odległości poszczególnych jego odcinków
n
∆
N l
l
i i
= ∑ E A (4)
i =1
i
i
2. Naprężenia dopuszczalne. Obliczenia wytrzymałościowe
Wzrost naprężeń i związanych z nimi odkształceń ciała powoduje zmiany w je-go stanie fizycznym, które prowadzą w rezultacie do odkształceń trwałych, a nawet zniszczenia spójności materiału. Zmiany te określa się jako wytężenie mate-
riału. Wzrost wytężenia mówi nam "o wyczerpywaniu wytrzymałości materiału".
Miarą wytężenia w przypadku osiowego działania siły w pręcie jest naprężenie normalne σ w jego przekroju. Próba rozciągania lub ściskania pozwala na wyzna-czenie naprężenia niebezpiecznego σnieb, za które w zależności od warunków można uznać Rm, R lub wytrzymałość na zmęczenie. W poprawnie zaprojektowa-e
nej konstrukcji wytężenie nie powinno nigdzie osiągnąć stanu niebezpiecznego.
W przypadku prętów rozciąganych (ściskanych) naprężenia σ powinny mieć wartość mniejszą niż naprężenia niebezpieczne. Tę dopuszczalną wartość naprężenia nazywa się naprężeniem dopuszczalnym σ
< σ
dop (σ dop
nieb).
σ
σ
nieb
=
dop
n
(5)
gdzie n > 1 - współczynnik bezpieczeństwa (pewności).
Współczynnik ten powinien uwzględniać prawdopodobieństwo zupełnie przypad-kowych odstępstw od warunków przyjętych za podstawę obliczeń. Można by się spodziewać, że współczynnik ten będzie niewiele większy od 1. W praktyce jed-nak współczynnik ten, odnoszący się do wytrzymałości Rm nierzadko osiąga wartość 6, a nawet 10. Właściwy dobór współczynnika bezpieczeństwa jest jednym z podstawowych zagadnień w nauce konstrukcji maszyn i wymaga dokładnej zna-jomości całokształtu problemów konstrukcyjnych, technologicznych i eksploata-cyjnych.
Podstawą do obliczeń wytrzymałościowych prętów poddanych działaniu siły osiowej jest równanie (1)
σ = N
σ ≤ σ
A i warunek
dop
2
Zależnie od tego, która z wielkości równania σ = N jest nieznana, rozróżnia się A
trzy typy obliczeń wytrzymałościowych.
2.1. Obliczenie sprawdzające
Dane są: siła podłużna N, kształt oraz wymiary przekroju pręta, a tym samym wielkość A i σ dop lub σ nieb. Wyznacza się wartość naprężeń normalnych σ i sprawdza, czy spełniony jest warunek σ ≤ σ dop
lub oblicza wartość współczynnika bezpieczeństwa
σ
n
nieb
= σ
2.2. Wyznaczenie obciążenia dopuszczalnego
Dane są: pole powierzchni przekroju pręta A i σ dop. Wyznacza się dopuszczalną wartość siły osiowej
N
= Aσ
dop
dop
a stąd w zależności od związków między obciążeniem P a siłą podłużną N - wartość obciążenia dopuszczalnego Pdop.
2.3. Wyznaczenie wymiarów
Dane są: siła podłużna N i naprężenie dopuszczalne σ dop. Wyznacza się konieczną wielkość przekroju.
N
A = σ
dop
Znając zaś A, oblicza się dla danego kształtu przekroju jego wymiary charaktery-styczne.
3
Wyszukiwarka
Podobne podstrony:
2 Rozc statycz wyznacz nap dop
2 Rozc statycz wyznacz nap dop
Linie wplywowe w ukladach statycznie wyznaczalnych belka3
Linie wplywowe w ukladach statycznie wyznaczalnych belka
8?danie przemieszczen ukladow statycznie wyznaczalnych a
Statyczna Wyznaczalność i Geometryczna Niezmienność to dwa podstawowe warunki
RAMA STATYCZNIE WYZNACZALNA
Linie wplywowe w ukladach statycznie wyznaczalnych belka2
linie wplywu w ukladach statycznie wyznaczalnych kratownica
Linie wpływowe sił w układach statycznie wyznaczalnych
kratownic statycznie wyznaczalnych
Belka statycznie wyznaczalna, labrysb2
Linie wplywowe w ukladach statycznie wyznaczalnych belka obwiednia
Linie wplywowe w ukladach statycznie wyznaczalnych kratownica3
więcej podobnych podstron