VI MODELE INWESTYCYJNE

___________________________________________________________________________

MODEL MARKOWITZA

1. Wstęp

Proces wyboru portfela inwestycyjnego można podzielić na trzy etapy: a) szacowanie rozkładu prawdopodobieństwa przyszłych stóp zwrotu, b) analizowanie oszacowanych rozkładów prawdopodobieństwa w celu określenia zbioru portfeli efektywnych,

c) dokonanie wyboru spośród portfeli efektywnych takiego, który jest najlepiej do-pasowany do preferencji inwestora.

Model stworzony przez Harry’ego Markowitza w 1952 r. odnosi się przede wszystkim do punktu b), tj. poszukiwania zbioru portfeli efektywnych. Markowitz zwrócił uwagę, że portfelem efektywnym nie jest portfel maksymalizujący oczekiwaną stopę zwrotu, bowiem kryterium maksymalizacji oczekiwanej stopy zwrotu nie uwzględnia pono-szonego ryzyka.

Portfel efektywny – portfel, który:

a) maksymalizuje oczekiwaną stopę zwrotu przy danym poziomie ryzyka, oraz b) minimalizuje ryzyko przy danym poziomie oczekiwanej stopy zwrotu.

Za miarę ryzyka w modelu Markowitza przyjęto odchylenie standardowe (wariancję) stopy zwrotu.

2. Opis modelu dwuskładnikowego

oznaczenia

R1 – oczekiwana stopa zwrotu z akcji pierwszej spółki R2 – oczekiwana stopa zwrotu z akcji drugiej spółki

σ1 – odchylenie standardowe stopy zwrotu z akcji pierwszej spółki σ2 – odchylenie standardowe stopy zwrotu z akcji drugiej spółki ρ1,2 – współczynnik korelacji między stopami zwrotu z akcji pierwszej i drugiej spółki w1 – wartościowy udział pierwszej akcji w portfelu

w2 – wartościowy udział drugiej akcji w portfelu

w1 + w2 = 1

charakterystyki portfela

R – oczekiwana stopa zwrotu z portfela

σ2 – wariancja stopy zwrotu z portfela

R = w R + w R

1

1

2

2

2

2

2

2

2

σ = w σ + w σ + 2 w w σ σ ρ

1

1

2

2

1

2

1

2

,

1 2

Na ogół rozważamy przypadek gdy R1 > R2 oraz σ1 > σ2.

- 1 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

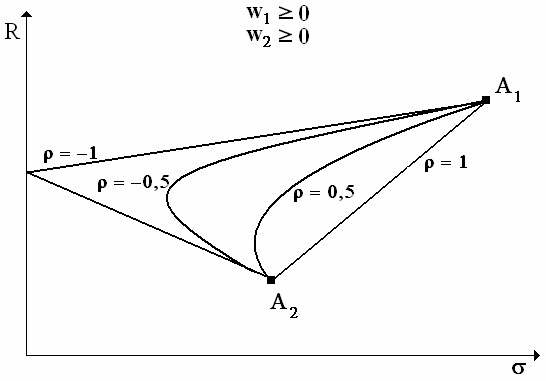
Zbiory możliwości (tj. zbiory wszystkich portfeli możliwych do utworzenia z danych dwóch akcji) dla różnych współczynników korelacji są przedstawione na poniższym wykresie (przy braku możliwości dokonywania krótkiej sprzedaży).

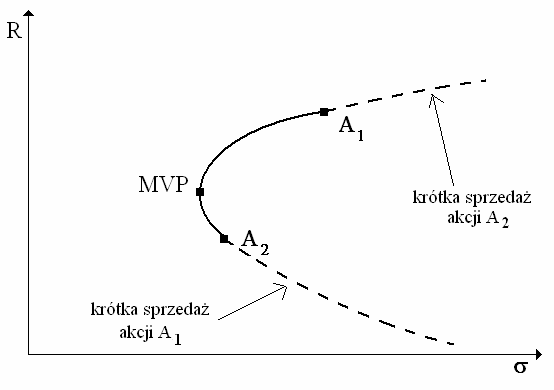
W przypadku, gdy dozwolona jest krótka sprzedaż wykres ten wygląda jak poniżej (dla współczynnika korelacji równego 0,5).

Dalej przyjmujemy, że krótka sprzedaż jest niedozwolona.

Jako MVP oznaczono portfel o minimalnej wariancji ( Minimum Variance Portfolio) –

jest to portfel złożony wyłącznie z akcji danych spółek (A1, A2), który cechuje się minimalną wariancją. Portfel taki można wyznaczyć ze wzorów: 2

σ −σ σ ρ

∗

2

1

2

,

1 2

w =

1

2

2

σ + σ − 2σ σ ρ

1

2

1

2

,

1 2

2

σ −σ σ ρ

∗

1

1

2

,

1 2

w =

2

2

2

σ +σ − 2σ σ ρ

1

2

1

2

,

1 2

- 2 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

przypadki szczególne – krótka sprzedaż niedozwolona ( w ≥ 0 , w ≥ 0 ) 1

2

(1) ρ1,2 = 1

2

σ

= ( w σ + w σ

1

1

2

)2

2

σ = w σ + w σ

1

1

2

2

∗

w = 0

1

⇒

σ

= σ

MVP

2

∗

w = 1

2

(2) ρ1,2 = 0

2

2

2

2

2

σ

= w σ + w σ

1

1

2

2

2

2

2

2

σ =

w σ + w σ

1

1

2

2

2

∗

σ 2

w =

1

2

2

σ +σ

1

2

σ σ

1

2

⇒

σ

=

MVP

2

2

σ + σ

1

2

2

∗

σ1

w =

2

2

2

σ + σ

1

2

(3) ρ1,2 = −1

2

σ

= ( w σ − w σ

1

1

2

)2

2

σ = w σ − w σ

1

1

2

2

∗

σ 2

w =

1

σ +σ

1

2

⇒

σ

= 0

MVP

∗

σ1

w =

2

σ + σ

1

2

- 3 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

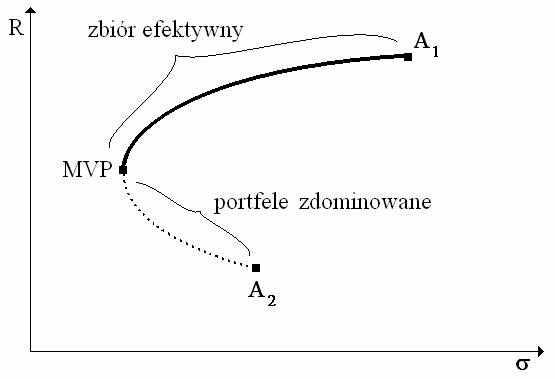
zbiór efektywny

Zbiór efektywny to zbiór portfeli efektywnych (niezdominowanych), czyli takich, któ-

re:

a) maksymalizują oczekiwaną stopę zwrotu przy danym poziomie ryzyka, oraz b) minimalizują ryzyko przy danym poziomie oczekiwanej stopy zwrotu.

portfele wieloskładnikowe

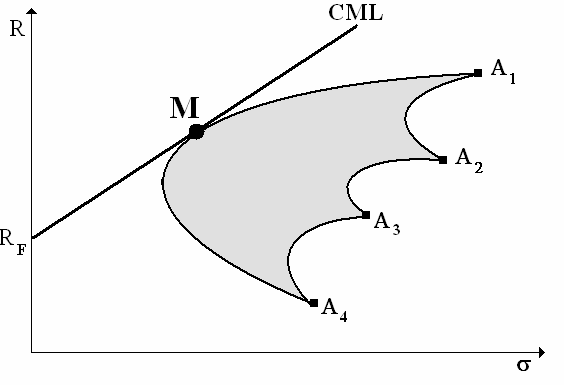
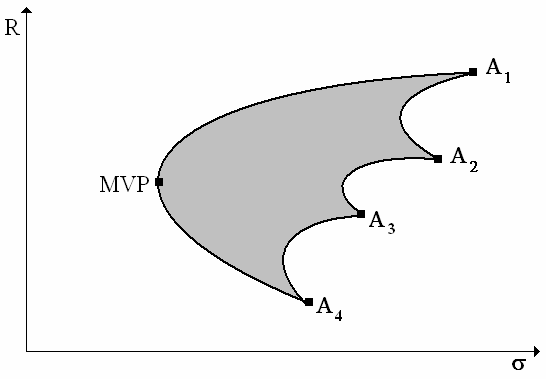
Dotychczas rozważano portfele złożone wyłącznie z dwóch akcji. Analizuje się także przypadek kiedy do portfela można włączyć więcej akcji. Wtedy zbiór możliwości in-westycyjnych przedstawia poniższy wykres.

Zbiór efektywny reprezentuje krzywa łącząca punkty MVP oraz A1. Można także wyznaczyć MVP analitycznie, jest to jednak zdecydowanie bardziej skomplikowane niż

w przypadku portfeli dwuskładnikowych.

- 4 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

portfele wieloskładnikowe złożone z aktywów ryzykownych oraz pozbawionych ryzyka Dotychczas rozważano portfele złożone wyłącznie z aktywów obarczonych ryzykiem.

Teraz zakładamy, że inwestorzy mogą także włączać do portfeli aktywa pozbawione ryzyka, np. bony skarbowe, bądź zaciągać kredyt. Przyjmujemy, że oprocentowanie bonów skarbowych i kredytu opisuje stopa procentowa wolna od ryzyka. Wtedy: R = α R + 1

( − α R

)

F

A

σ = 1

( − α σ

) A

gdzie:

R – oczekiwana stopa zwrotu z portfela

α - wartościowy udział instrumentów pozbawionych ryzyka w portfelu RF – stopa procentowa wolna od ryzyka

RA – oczekiwana stopa zwrotu z portfela akcji

σA – odchylenie standardowe stopy zwrotu z portfela akcji Zbiór efektywny jest półprostą oznaczoną jako CML (M oznacza portfel rynkowy).

Capital Market Line (CML) – linia przedstawiająca zbiór portfeli efektywnych w sytu-acji, gdy dopuszczalne jest inwestowanie (pożyczanie) w instrumenty pozbawione ryzyka; część prostej o równaniu:

R − R

m

F

R = R +

σ

F

σ m

gdzie:

R – oczekiwana stopa zwrotu z portfela efektywnego

RF – stopa procentowa wolna od ryzyka

Rm – oczekiwana stopa zwrotu z portfela rynkowego

σm – odchylenie standardowe stopy zwrotu z portfela rynkowego σ – odchylenie standardowe stopy zwrotu z portfela efektywnego Jedynym portfelem efektywnym złożonym wyłącznie z aktywów ryzykownych jest portfel rynkowy (M).

- 5 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

MODEL MARKOWITZA - ZADANIA

Zad.1.

Oblicz oczekiwaną stopę zwrotu oraz odchylenie standardowe portfela o poniższych parame-trach:

Spółka

Ilość akcji

Cena akcji

PKO BP

100

30 zł

Lotos

400

17,50 zł

Charakterystyki akcji:

Oczekiwana

Odchylenie

Współczynnik

Spółka

stopa zwrotu

standardowe

korelacji

PKO BP

5%

10%

0,6

Lotos

12%

18%

Zad.2.

Wykonaj polecenia dysponując danymi z poniższej tabeli: General

Miara \ Spółka

Apple

AT&T

Motors

Oczekiwana stopa zwrotu

14%

5%

9%

Odchylenie standardowe

25%

15%

20%

Spółka

Współczynniki korelacji

Apple

-

0,4

0

AT&T

-

-

0,6

General Motors

-

-

-

a) oblicz oczekiwaną stopę zwrotu i odchylenie standardowe portfela złożonego w 40% z akcji Apple oraz w 60% z akcji AT&T,

b) oblicz oczekiwaną stopę zwrotu i odchylenie standardowe portfela złożonego w 20% z akcji Apple oraz w 80% z akcji General Motors,

c) oblicz oczekiwaną stopę zwrotu i odchylenie standardowe portfela złożonego w 55% z akcji AT&T oraz w 45% z akcji General Motors,

d) wyznacz portfel o minimalnej wariancji złożony z akcji Apple i AT&T, e) wyznacz portfel o minimalnej wariancji złożony z akcji Apple i General Motors, f) wyznacz portfel o minimalnej wariancji złożony z akcji AT&T i General Motors.

Zad.3.

Dane są akcje dwóch spółek: A i B. Ich parametry przedstawiono w tabeli: Oczekiwana

Odchylenie

Spółka

stopa zwrotu

standardowe

A

9%

21%

B

17%

29%

- 6 -

 by Rafał Buła

VI MODELE INWESTYCYJNE

___________________________________________________________________________

Wiedząc, że krótka sprzedaż jest niedopuszczalna, wyznacz portfel o minimalnej wariancji, jeżeli współczynnik korelacji wynosi:

a) 1,

b) 0,5,

c) 0,

d) -1,

Oblicz ich oczekiwaną stopę zwrotu i odchylenie standardowe.

Zad.4.

Wiedząc, że:

a) stopa zwrotu z bonów skarbowych wynosi 4%,

b) oczekiwana stopa zwrotu z portfela rynkowego wynosi 12%, c) oczekiwana stopa zwrotu z portfela efektywnego o odchyleniu standardowym równym 18% wynosi 13%,

oblicz wariancję stopy zwrotu z indeksu rynkowego. Podaj równanie linii CML. Sprawdź, czy portfel o odchyleniu standardowym równym 14% i oczekiwanej stopie zwrotu wynoszą-

cej 9% jest efektywny.

- 7 -

 by Rafał Buła