1.
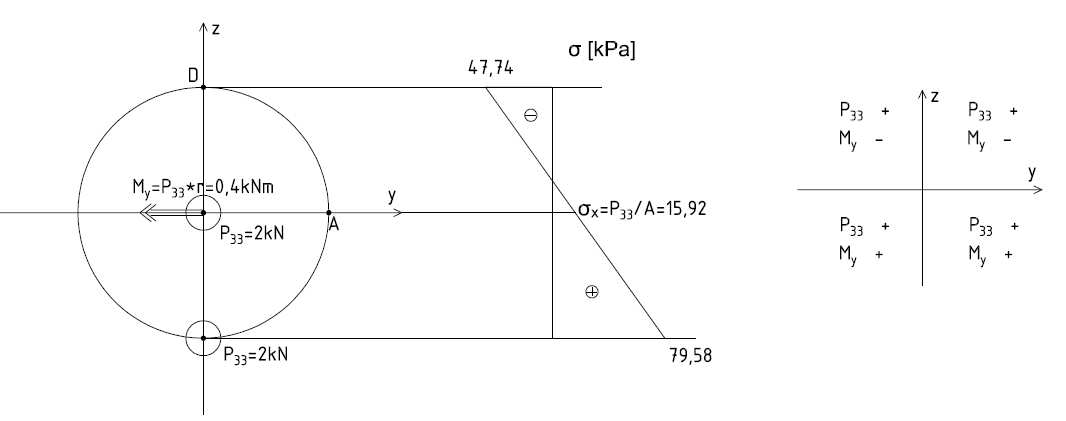
a) naprężenia od siły p 33
P
M
σ
= 33
y⋅ Z
x min
A
I y
A=π⋅ r 2=3,14⋅(0,2)2=0,1256 m 2
π⋅ r 4
I = I =
=3,14⋅(0,2)4=1,256⋅10 3 m 4
y
z
4
4
σ
=
2
0,4
⋅0,2= 47,74 kPa
x min
0,1256
1,256⋅10 3
P
M
σ
= 33+
y⋅ Z
x max
A
I y
σ
=
2
+
0,4
⋅0,2=79,58 kPa
x max
0,1256
1,256⋅10 3
Q=0 →τ =0
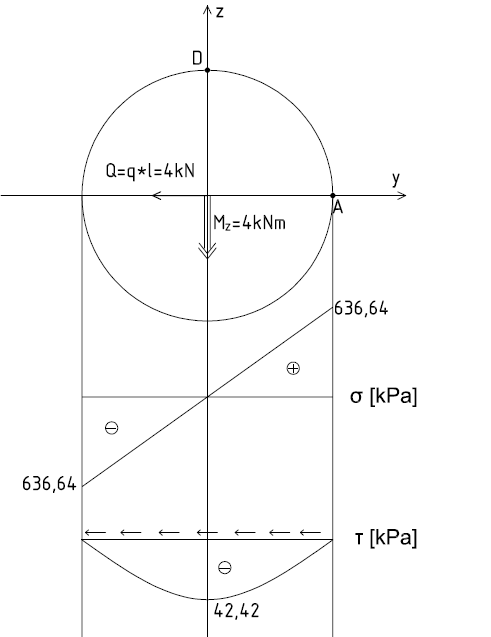
b) naprężenia od obciążenia q π⋅ r 2
S =
⋅4⋅ r = 3,14⋅(0,2)2⋅ 4⋅0,2 =5,33⋅10 3 m 3
z
2
3⋅π
2
3⋅3,14
M
σ
=
z⋅ y=
4
⋅0,2=636,64 kPa
x max
I z
1,256⋅10 3
M
σ
=
z⋅ y=
4
⋅0,2= 636,64 kPa
x max
I z
1,256⋅10 3
Q⋅ S
τ
=
z
= 4⋅5,33⋅10 3 =42,42 kPa max
I ⋅ h( z ) z
1,256⋅10 3⋅0,4
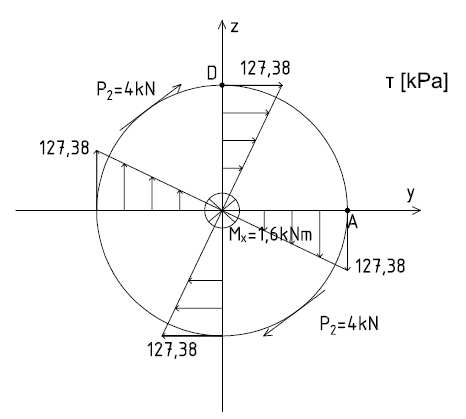
c) naprężenia od siły p 2 (momentu skręcającego) σ =0
x
M
τ =
x⋅ρ
I 0
ρ= r =0,2 m I = I + I =2,512⋅10 3 m 4
0
y
z
τ =
1,6
⋅0,2=127,38 kPa
2,512⋅10 3
d) naprężenia a punktach A i D
-w punkcie A
σ =σ ( p )+σ ( q)=15,91+636,64=652,55 kPa x
33
τ =τ ( p )= 127,38 kPa 2
σ =σ ( p )= 47,74 kPa x
33
τ =τ ( p )+τ ( q)= 42,42+127,38=84,96 kPa 2
Wyszukiwarka
Podobne podstrony:
projekt 81
projekt 81 życzenia DMR 1807
Zdrowie z przekazow EN-KI Sesje 81-100, Projekt Cheops -Lucyna Lobos
projekt o narkomanii(1)
!!! ETAPY CYKLU PROJEKTU !!!id 455 ppt
Wykład 3 Dokumentacja projektowa i STWiOR
Projekt nr 1piątek
Projet metoda projektu
34 Zasady projektowania strefy wjazdowej do wsi
PROJEKTOWANIE ERGONOMICZNE
Wykorzystanie modelu procesow w projektowaniu systemow informatycznych
Narzedzia wspomagajace zarzadzanie projektem
Zarządzanie projektami 3
Metody Projektowania 2
więcej podobnych podstron