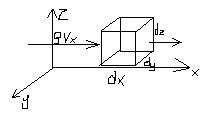
12 równanie ciągłości – ruch nieustalony płynu ściśliwego Przy przepływie przestrzennym, gdzie wyznaczamy składowe prędkości Vx,Vy,Vz ciśnienie p i ρ jako funkcję współrzędnych x, y, z równania ciągłości wyprowadza się z równania masy płynu, która wypływa z elementarnego sześcianu o krawędziach dx, dy, dz .
∂(ρ V )
- ρ V
x
+
dx
x
x
∂
Nieustawny przepływ płynu ściśliwego gdzie gęstość ρ(x, y, z, t)=0. W czasie dt w kierunku osi x wpływa do elementu przez lewą ścianę o powierzchni dydz masa płynu ρ Vxdzdydt.
Przez przeciwległą ściankę w tym samym czasie wypływa masa płynu.
∂(ρ V )
ρ V
x
+
dx dydzdt
x
x
∂
przyrost masy w czasie dt w kierunku osi x
∂( V
ρ
∂ ρ
x )
( Vx)
ρ V dydzdt − V
ρ +
dx dydzdt = −
dxdydzdt
x
x
x
∂
x
∂
Analogicznie przyrost masy przy przepływie w kierunku y i z wynoszą:
∂( V
ρ
∂
y )
( Vz )
−
ρ
dxdydzdt
;
−
dxdydzdt
y
∂
z
∂
Suma przyrostów mas w elemencie płynu w kierunku wszystkich osi:
∂( V
ρ ) ∂(ρ V
∂ ρ
y
x
) ( Vz)
−
+
+
+ dxdydzdt
x
∂
y
∂
z
∂
Równocześnie jednak mamy gęstość ρ która w czasie t wynosiła ρ(x,y,z,t), więc w czasie t+dt gęstość ρ(x,y,z,t+dt)= ρ+(ل ρ/لt)*dt W czasie dt masa płynu wewnątrz elementu zmieni się od wartości ρ(dxdydz) do
[ ρ(ل ρ/لt)*dt]dxdydz. Stąd przyrost masy - ρ dxdydz+[ ρ+(ل ρ/لt)*dt]dxdydz = (ل ρ/لt)dxdydzdt.
Porównując przyrosty otrzymujemy:
∂(ρ V ) ∂(ρ V
ρ
ρ
ρ
ρ
ρ
ρ
y
x
) ∂( Vz)
∂
∂
∂( V ) ∂( Vy x
) ∂( Vz)
−
+
+
+ dxdydzdt =
dxdydzdt ⇒
+
+
+
= 0
∂ x
∂ y
∂ z
∂ t
∂ t
∂ x
∂ y
∂ z
{różnicowe równanie ciągłości ruchu nieustalonego płynu ściśliwego.
∂( V
ρ
∂
∂ρ
∂
∂ρ
x )
V
V
dx
x
= ∫
+
V
x
= ∫
+
x
∂
∂
∂
∂
∂
∂( x
x
x
x
x dt
ρ V
∂
∂ρ
∂
∂ρ
y )
lub :
V
V
y
y
dy
= ∫
+
V = ∫
+
y
∂
y
∂
y y
∂
y
∂
y
∂ dt
∂( V
ρ
∂
∂ρ
∂
∂ρ
z )
V
V
dz
z
= ∫
+
V
z
= ∫
+
z
∂
z
∂
z z
∂
z
∂
z
∂ dt
Podstawiając do równania ciągłości :
∂ρ ∂ρ dx ∂ρ dy ∂ρ dz
∂ V
∂ Vy
x
∂ V
+
+
+
+ ρ
+
+
z
= 0
∂ t
∂ x dt ∂ y dt ∂ z dt
∂ x
∂ y
∂ z
dp
r
+ ρ di V
v
= 0 → równanie ciągłości ruchu nieustalonego płynu ściśliwego.
dt
Wyszukiwarka
Podobne podstrony:
12 równanie ci1g3osciid 13586
12 równanie ciągłości, mechanika plynów
Zestaw 12 Macierz odwrotna, układy równań liniowych
12 ELEMENTY RÓWNAŃ RÓŻNICZKOWYCH ZWYCZAJNYCH
METODA 3 RÓWNAŃ- wzorki, NAUKA, budownictwo nowe 4.12.2011, Materiały budowlane
uklady rownan nieliniowych 0.12
12 Uklady rownan
LISTA 12 Zwyczajne, liniowe równania różniczkowe II go rzędu o stałych współczynnikach
Zestaw 12 Macierz odwrotna, układy równań liniowych
Edytor rownan 2003 12
Macierze,wyznaczniki, układy równań AK, 2011 12
wykład 12 pamięć
Rozwiązywanie układów równań
więcej podobnych podstron