12 równanie ciągłości - ruch nieustalony płynu ściśliwego

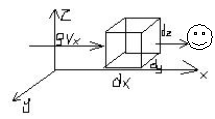
Przy przepływie przestrzennym, gdzie wyznaczamy składowe prędkości V_x,V_y,V_z ciśnienie p i ρ jako funkcję współrzędnych x, y, z równania ciągłości wyprowadza się z równania masy płynu, która wypływa z elementarnego sześcianu o krawędziach dx, dy, dz .

☺-

Nieustawny przepływ płynu ściśliwego gdzie gęstość ρ(x, y, z, t)=0. W czasie dt w kierunku osi x wpływa do elementu przez lewą ścianę o powierzchni dydz masa płynu ρV_xdzdydt. Przez przeciwległą ściankę w tym samym czasie wypływa masa płynu.

przyrost masy w czasie dt w kierunku osi x

Analogicznie przyrost masy przy przepływie w kierunku y i z wynoszą:

Suma przyrostów mas w elemencie płynu w kierunku wszystkich osi:

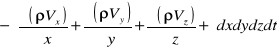
Równocześnie jednak mamy gęstość ρ która w czasie t wynosiła ρ(x,y,z,t), więc w czasie t+dt gęstość ρ(x,y,z,t+dt)=ρ+(لρ/لt)_*dt

W czasie dt masa płynu wewnątrz elementu zmieni się od wartości ρ(dxdydz) do [ρ(لρ/لt)_*dt]dxdydz. Stąd przyrost masy -ρdxdydz+[ρ+(لρ/لt)_*dt]dxdydz = (لρ/لt)dxdydzdt. Porównując przyrosty otrzymujemy:

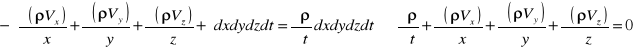
{różnicowe równanie ciągłości ruchu nieustalonego płynu ściśliwego.

lub :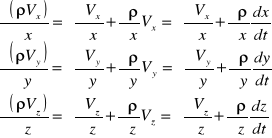

Podstawiając do równania ciągłości :

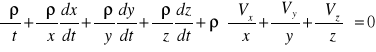
→ równanie ciągłości ruchu nieustalonego płynu ściśliwego.

---