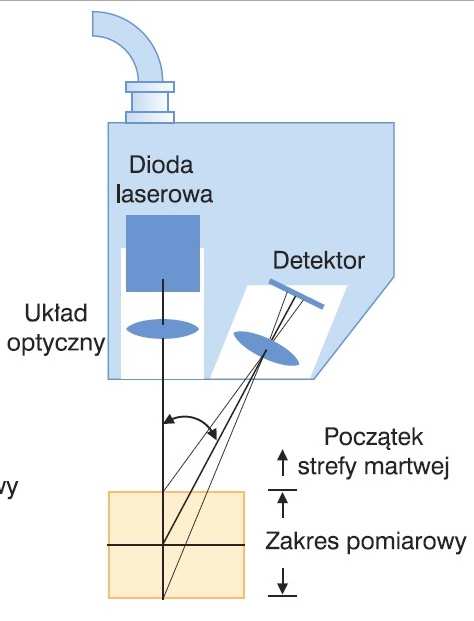
1. Budowa i zasada działania czujnika laserowego używanego do pomiarów wielkości kinetycznych.

Promień lasera odbijając się od ruchomego przedmiotu, po przejściu przez układ optyczny przyrządu, trafia na różne punkty elementu światłoczułego, zależne od odległości czujnika od przedmiotu.

Pozycja promienia padającego na element światłoczuły zostaje zidentyfikowana przez układ elektroniczny i przekazana na wyjście napięciowe przyrządu. Zaletą omawianego typu czujnika jest duża rozdzielczość, stosunkowo niska cena porównywalna do ceny zestawu akcelerometr – prosty wibrometr.

2. W jaki sposób, krok po kroku, dokonuje się pomiarów za pomocą szybkiej kamery.

Zasada tych pomiarów jest dla wszystkich technik wspólna: rejestrowana jest sekwencja kolejnych położeń badanych punktów ruchomego ciała, a później analizowany jest zarejestrowany materiał

i obliczane wielkości kinematyczne interesujących punktów.

Wykonanie ćwiczenia

Ćwiczenie jest wykonywane na stanowiskach komputerowych. Podstawą ćwiczenia są dwa filmy zarejestrowane szybką kamerą Kodak z częstotliwością 1000 klatek na sekundę. Filmy przedstawiają rękę człowieka poddaną wibracjom miejscowym podczas wiercenia wiertarką. Zadaniem uczestników ćwiczenia jest komputerowa analiza zarejestrowanych filmów w celu:

-

otrzymania przebiegów czasowych przyspieszenia punktów na ręce i wiertarce,

-

obliczenia wartości skutecznej i wartości szczytowej przyspieszenia punktów na wiertarce i ręce operatora,

-

obliczenia współczynnika szczytu,

-

porównanie uzyskanych wielkości z wartościami dopuszczalnymi,

-

wykonanie analizy częstotliwościowej otrzymanych przebiegów czasowych,

-

wnioski

Podczas analizy zastosuj podaną niżej procedurę:

-

otwórz program Image Express Vision

-

zamknij okno z wiertarką w pozycji poziomej,

-

włącz odtwarzanie filmu i zaobserwuj wibracje ręki i rękojeści,

-

wyłącz odtwarzanie,

-

włącz rysowanie wykresu i skonfiguruj go jako wykres przyspieszenia składowej x w funkcji czasu,

-

zaznacz punkty 1, 2, 3 i 4,

-

kliknij dwukrotnie wykres i zapisz dane w formie macierzy,

-

zapisaną macierz skonfiguruj tak by uzyskać równe odstepy w kolumnie czasu

-

skonfigurowaną macierz załaduj do programu LabView Signal Express,

-

wykorzystując kolejne kroki programu uzyskaj przebiegi czasowe przyspieszenia odpowiednich punktów, zmień jednostki na SI, oblicz wartości skuteczne i szczytowe uzyskanych przebiegów,

-

wykonaj analizę widmową uzyskanych przebiegów

-

wykonaj te same czynności dla składowej y przyspieszenia.

3. Co otrzymuje się podczas analizy modalnej

Analiza modalna jest często stosowaną w praktyce techniką badania własności dynamicznych obiektów mechanicznych. W wyniku analizy modalnej otrzymuje się model modalny w postaci zbioru częstotliwości własnych, postaci drgań oraz współczynników tłumienia. Znajomość tych parametrów pozwala na przewidywanie zachowania się obiektu na skutek dowolnych zaburzeń równowagi. Jest ona stosowana dla celów modyfikacji konstrukcji, diagnostyki stanu konstrukcji, weryfikacji i dostrajania modeli numerycznych, do syntezy układów sterowania oraz diagnostyki maszyn opartej o śledzenie zmian parametrów modeli wraz ze zmianą stanu badanego obiektu.

W klasycznym sformułowaniu wykonuje się eksperyment, w którym wymusza się ruch obiektu za pomocą znanych sił oraz mierzy odpowiedź układu w sieci punktów pomiarowych rozłożonych na obiekcie. Na podstawie zmierzonych sygnałów wymuszających i odpowiedzi układu wyznacza się model funkcjonalny w postaci charakterystyk czasowych lub częstotliwościowych i na ich podstawie dokonuje się estymacji parametrów modelu modalnego.

Analiza modalna wymaga spełnienia założeń:

- układ jest liniowy opisany równaniami różniczkowymi liniowymi

o stałych współczynnikach

-

układ jest obserwowalny i istnieje możliwość pomiaru wszystkich charakterystyk niezbędnych do identyfikacji

-

układ spełnia zasadę wzajemności Maxwella

-

tłumienie w układzie jest małe

4. Do czego w analizie modalnej służy koherencja.

Dzięki koherencji możemy sprawdzić czy i w jakim stopniu sygnał zadany i odebrany są zgodne w fazie.

2

G ( f )

2

xy

γ ( f ) =

xy

G ( f ) G ( f )

x

y

Funkcja koherencji:

2

- γ xy ≤ 1

2

-gdy dla pewnej częstotliwości

γ xy = 0

wówczas x(t) i y(t) są niekoherenntne

- gdy dla pewne j czestotliwości

2

γ xy =1

Wówczas sygnały te są koherentne

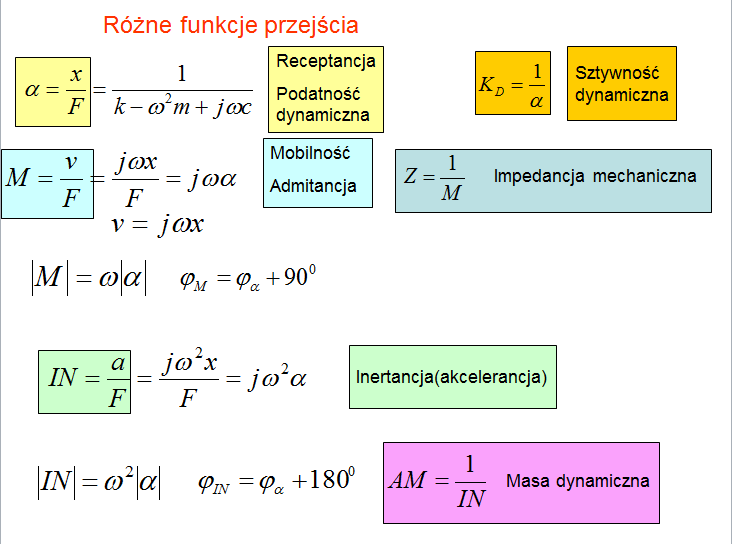
5. Wymienić funkcje przejścia w analizie modalnej

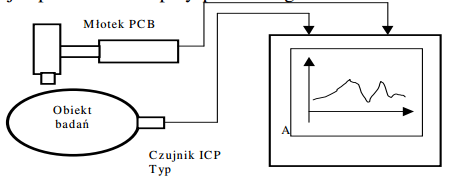
6. Jak wykonuje się kalibracje przy pomiarach szybka kamera

Kalibracja polega na przedstawieniu na jednej z klatek znacznika przedstawiając znany nam wymiar przedmiotu program sczyta ilość pikseli a my podamy mu wielkość w mm. Dzięki temu dostaniemy wyniki w jednostkach Si.

7. Budowa młotka modalnego

Młotek modalny wizualnie nie różni się od klasycznego młotka, posiada natomiast wbudowany w części głowy akcelerometr do pomiaru siły uderzenia z wyprowadzeniami sygnału w dolnej części trzonka.