Czy politycy kłamią,

czyli początki

przekształcenia

Fouriera

Dla przypomnienia:

(bajka)

Pewnego dnia Luke Skywalker zaczął się tak mocno
jąkać, że udusił się i umarł. Trafił do nieba i w
poczekalni widzi mnóstwo zegarów, z których każdy
pokazuje inną godzinę. A cóż to? Pyta Świętego Piotra.
Ano każdy człowiek przy urodzeniu dostaje zegar
ustawiony na godzinę 12. Za każdym razem gdy
człowiek skłamie wskazówka przesuwa się o minutę. O
tu jest zegar Matki Teresy z Kalkuty, cały czas wskazuje
12:00. No dobra, o gdzie są zegary Lorda Vadera,
komandora Tarkina i Dartha Maula? pyta Luke. A, tych
używamy jako wentylatorów w świetlicy.

Matka Teresa – sygnał stały.

Wskazówka pozostaje w

miejscu

Lord Vader –

sygnał zmienny

(narodziny)

1 kłamstwo

(wskazówka

nieco się

obróciła)

drugie,

i tak

dalej ...

kąt 

W miarę upływu czasu (kolejnych kłamstw

Lorda) kąt  ulega zmianie

Z – położenie końca

wskazówki

Zauważmy, że taki eksperyment myślowy od
razu narzuca dyskretną dziedzinę sygnału (nie
wyróżniamy czegoś takiego jak pół kłamstwa).
Zatem

kolejne

kłamstwa

Vadera

można

ponumerować

(indeksować

liczbami

naturalnymi)



1



2



3

(kąt) zmienia się z kolejnymi

kłamstwami...

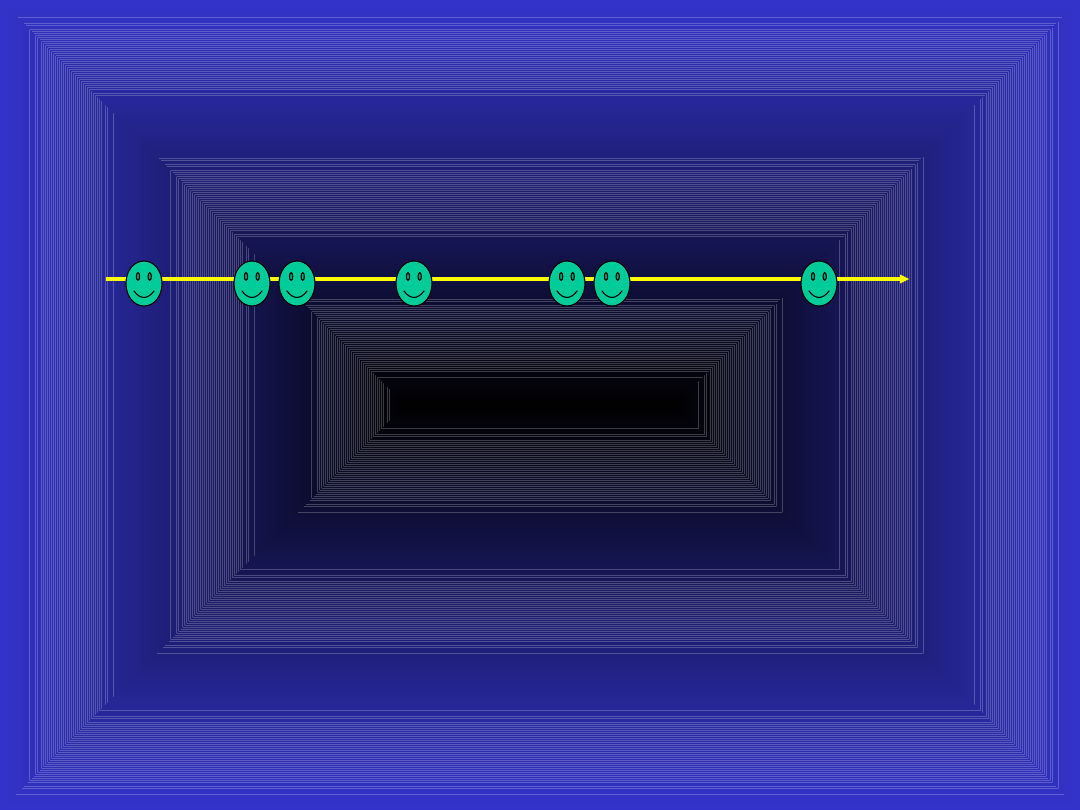
Jest pewien problem: otóż indeksujemy sygnał
kolejnymi kłamstwami:

Brakuje

relacji

czasowej

między

kolejnymi

kłamstwami.

k=0

k=1

k=2

k=3...

czas

Opisywany

w

doświadczeniu

zegar

w

rzeczywistości zegarem nie jest ponieważ nie
tyka równo...

Vader kłamie pierwszy raz w życiu:
„zegar” przeskakuje o minutę...

...z tym że przez dwadzieścia lat
jest superszlachetnym rycerzem
Anakinem i nie kłamie. W pewnym
momencie przechodzi na Ciemną
stronę i zaczyna łgać jak bura
suka.

Wskazówka przeskakuje o

jedną

minutę

po

dwudziestu

latach...

Potem jest już z górki i Lord pogrąża się całkowicie
w szerzeniu intryg imperium zła. Wskazówka
zaczyna tykać z ogromną, nieprzewidywalną
częstością (na przykład 5 razy na sekundę)

Wprowadzając dodatkowe założenie synchronizujemy
„zegar”. Tyka on z częstotliwością np. 5 Hz. Innymi
słowy

częstotliwość

generowania

sygnału

wynosi 5 Hz. „k” służy teraz do indeksowania
równych odstępów czasu wynoszących 1/5 s. Kąt
zależy od czasu wprost:

k

k

60

2

)

(







g

kf

t

k

t

60

2

/

60

2

)

(













Z1

Z1

Z3

Z4

Dodatkowo

kłamstwo

kłamstwu

nierówne. Kolejne wypowiedzi Lorda
mogą mieć różny „ciężar gatunkowy”.
Niech długość wskazówki czyli moduł
określa tę właśnie wielkość.

Zatem sygnał zespolony określają
dwie wielkości zależne od indeksu k
(numeru kłamstwa): kąt oraz moduł

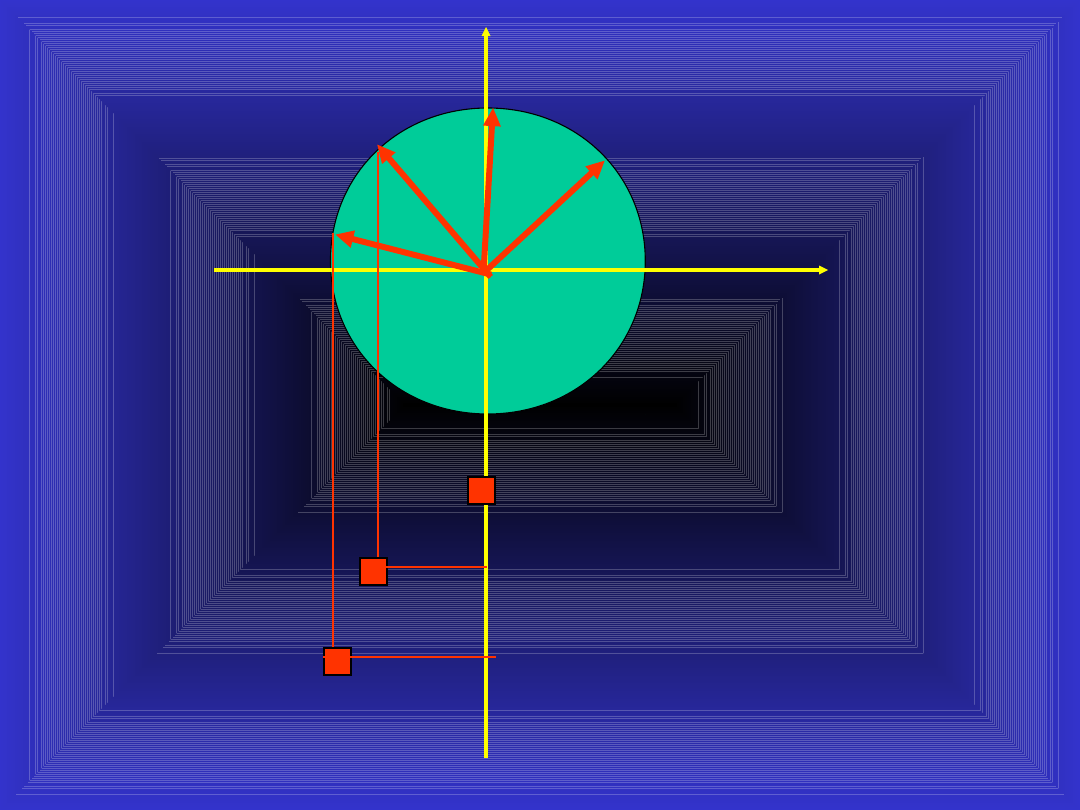
stosunek Imperatora do Vadera
(część rzeczywista Z)

urojenia Vadera

zakładamy,

że

wszystkie kłamstwa są
równie wstrętne

ponieważ

założyliśmy

stałość

odcinków

czasowych

dzielących

kolejne próbki sygnału, możemy
dokonać projekcji Z na oś rzeczywistą
otrzymując

biorytm

humoru

Imperatora

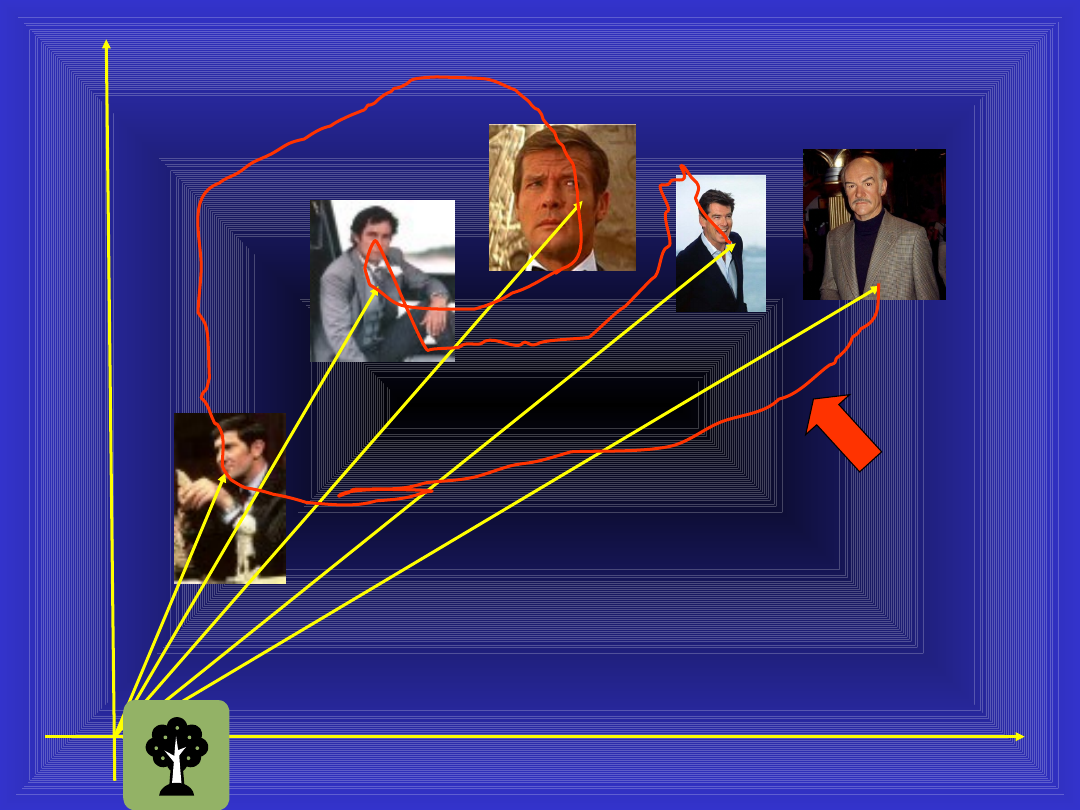
17 listopada

przystojność

talent

B.M.

sygnał
„Bond,
James
Bond”

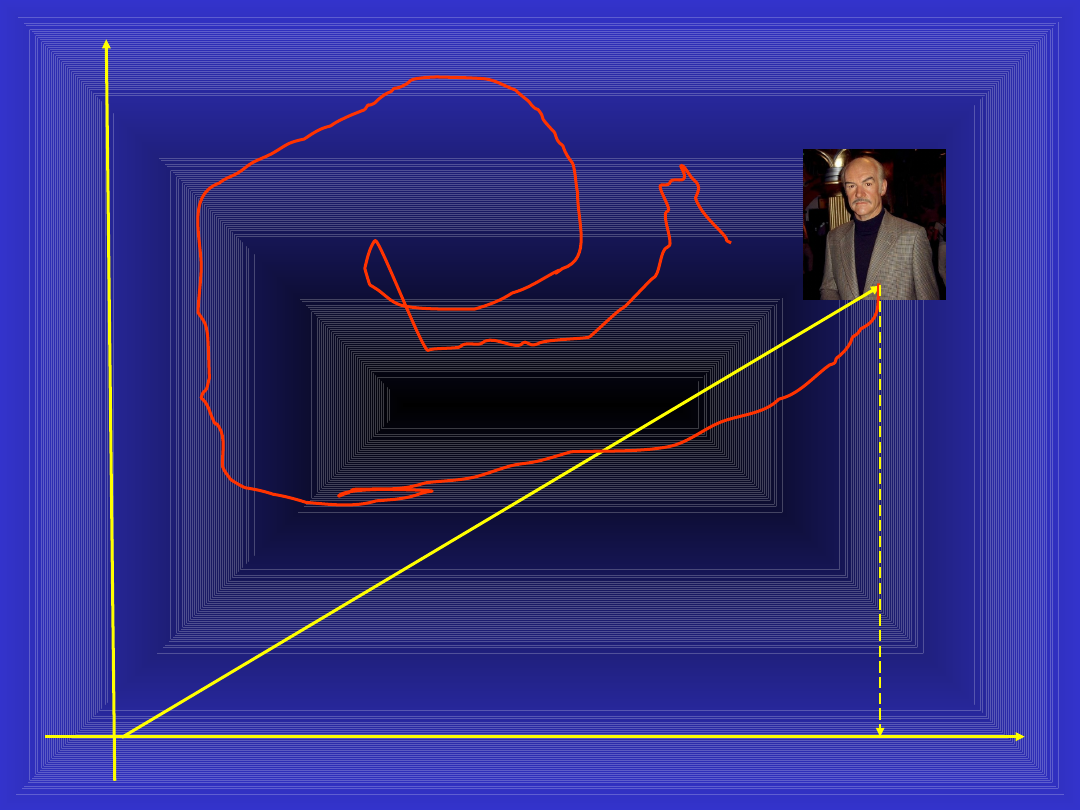
przystojność

talent

rzut

projekcja

Fourier

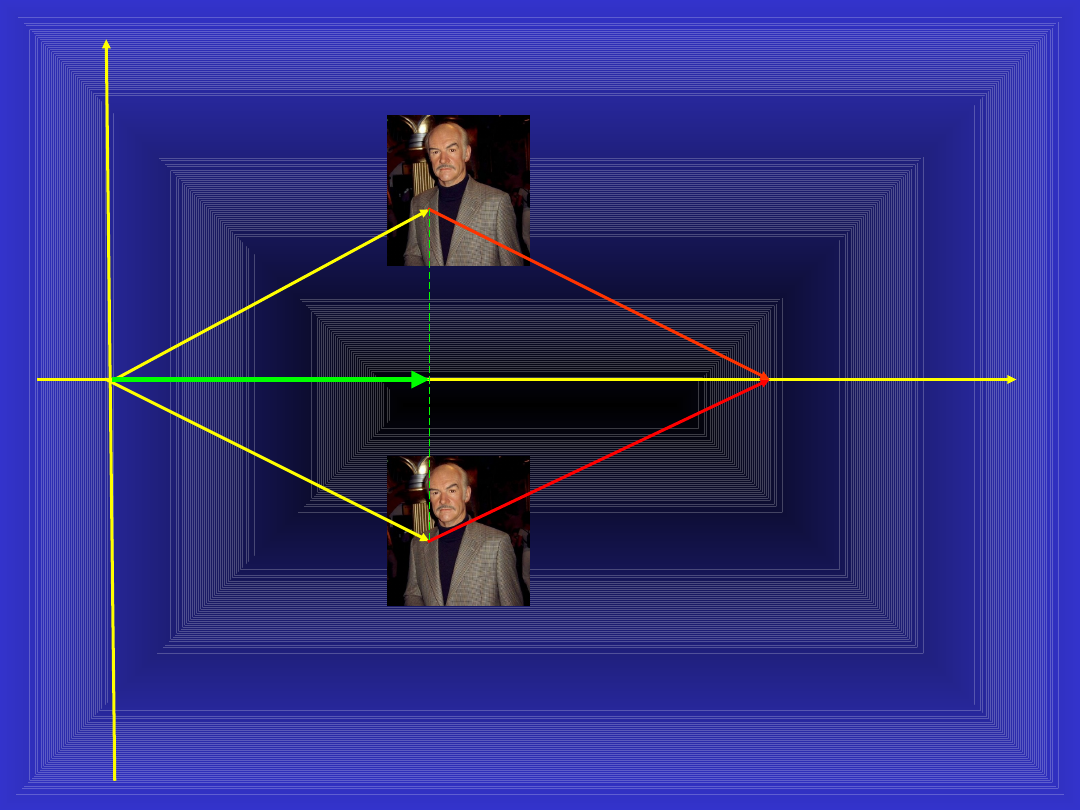
przystojność

talent

minus Sean

dwa Seany / 2

Wnioski

Sygnał może być reprezentowany przez ruch punktu
„Z” na płaszczyźnie zespolonej.

Odległość punktu od początku układu współrzędnych
to moduł liczby zespolonej. Kąt pomiędzy osią x
(rzeczywistą) to kąt fazowy (faza).

Obie wielkości opisane powyżej są funkcjami czasu
(dyskretnego lub ciągłego).

Elementarnym sygnałem jest krążenie punktu „Z” po
okręgu ze stałą prędkością.

Co ma do tego Fourier?*

Jan Baptysta Józef Fourier urodził się 21 marca 1768
w Auxerre. Zainteresowania matematyczne łączył z
działalnością

polityczną.

Dwukrotnie

uniknął

gilotyny

w

czasie

Rewolucji

Francuskiej.

Współpracował z Napoleonem Bonaparte, który w
1802 mianował go prefektem dzielnicy Francji z
siedzibą w Grenoble. Kluczowa praca Fouriera
powstała w 1807. Inne ważne nazwiska związane z
tematem to Lagrange, Laplace, Bernoulli i Euler.