Cegły i pustaki

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Przedstawiony algorytm dyskretnego przekształcenia Fouriera
umożliwia wydzielanie składowych częstotliwościowych czyli
materiału budulcowego przebiegów. Jednak przebiegi dyskretne
zawierają „puste przestrzenie” pomiędzy kolejnymi próbkami.
Prześledzimy w jaki sposób wykonywana jest analiza takich
sygnałów.

Poprawny sygnał

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

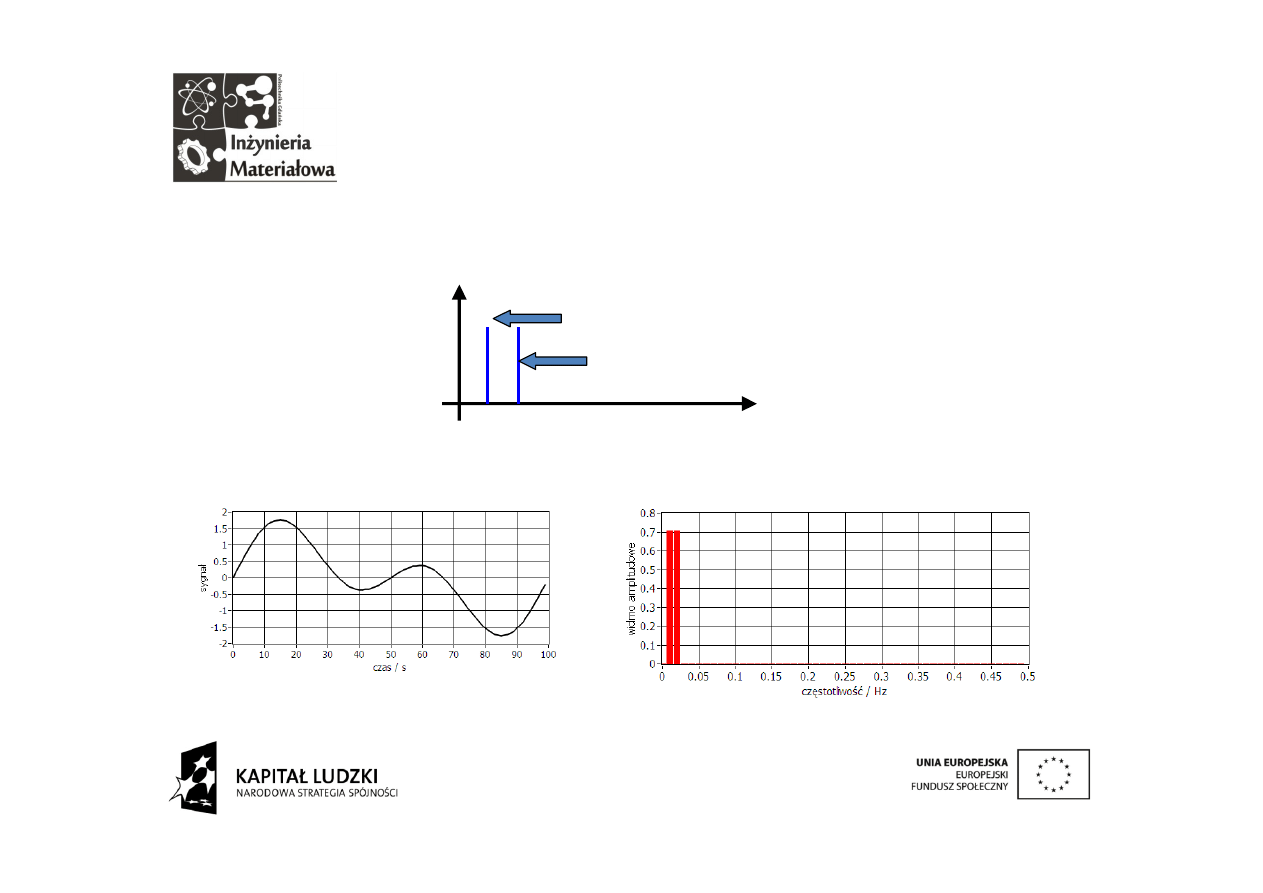
Na początku próbkowaniu poddamy sygnał zawierający dwie składowe
f

1

=

0,01 Hz i f

2

=

0,02 Hz. Postać widma amplitudowego takiego sygnału nie

jest niczym nowym:

częstotliwość

f

1

=0,01

f

2

=0,01

Sygnał spróbkowany i jego widmo również nie jest podejrzany:

Widmo jest automatycznie ograniczane do zakresu

0

÷f

p

/2

Sabotaż

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Sygnał analogowy jest sygnałem okresowym. Częstotliwość podstawowa
wynosi w tym przypadku 0,01 Hz a częstotliwość drugiej składowej to jej
pierwsza wielokrotność, lub jak się czasem mawia pierwsza harmoniczna.
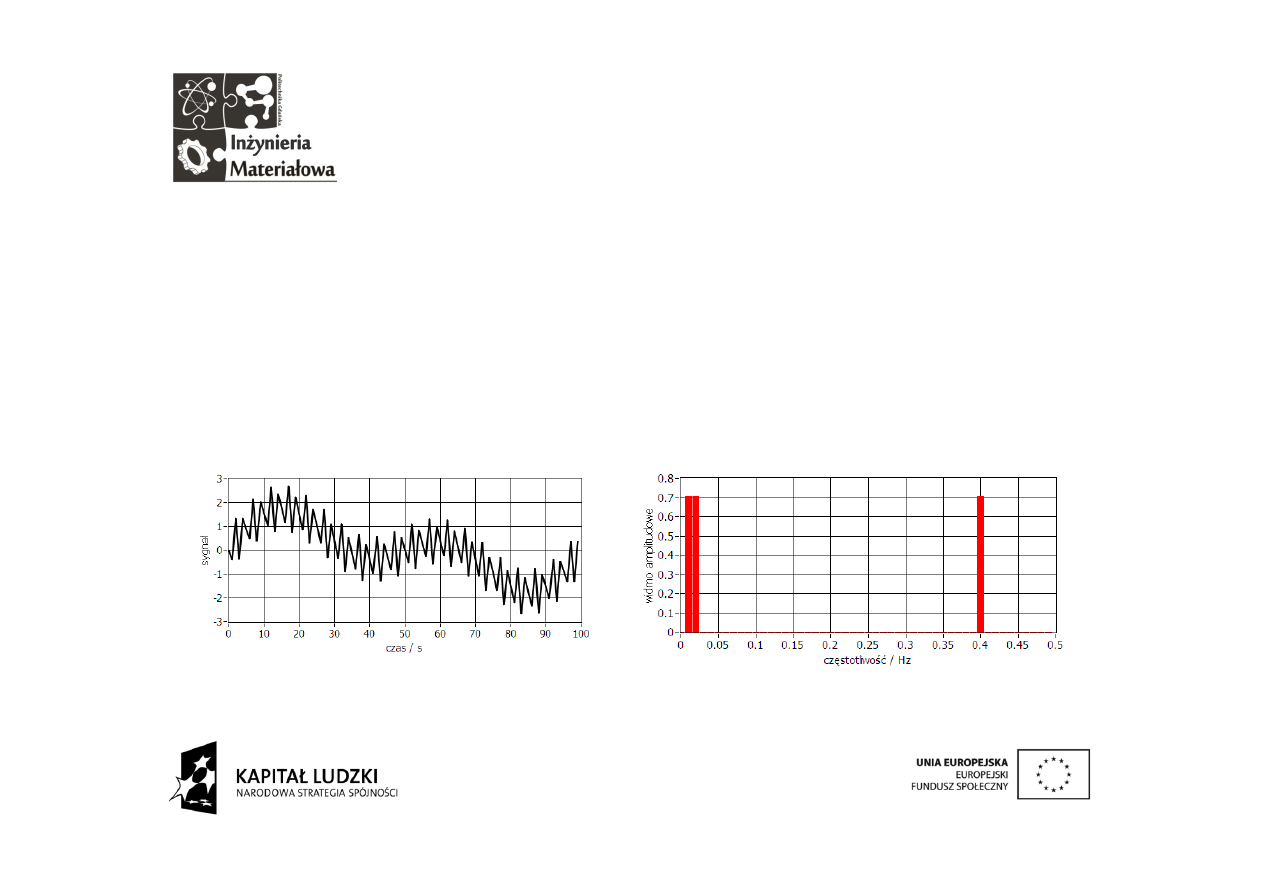
Dokonamy sabotażu wprowadzając do sygnału składową o częstotliwości
0,6 Hz czyli powyżej połowy częstotliwości próbkowania. Jest to 60
wielokrotność. Skoro występują wymierne wielokrotności częstotliwości
podstawowej to sygnał nadal jest okresowy.

Prążek 0,4 Hz to znany nam już alias będący efektem powielenia widma.

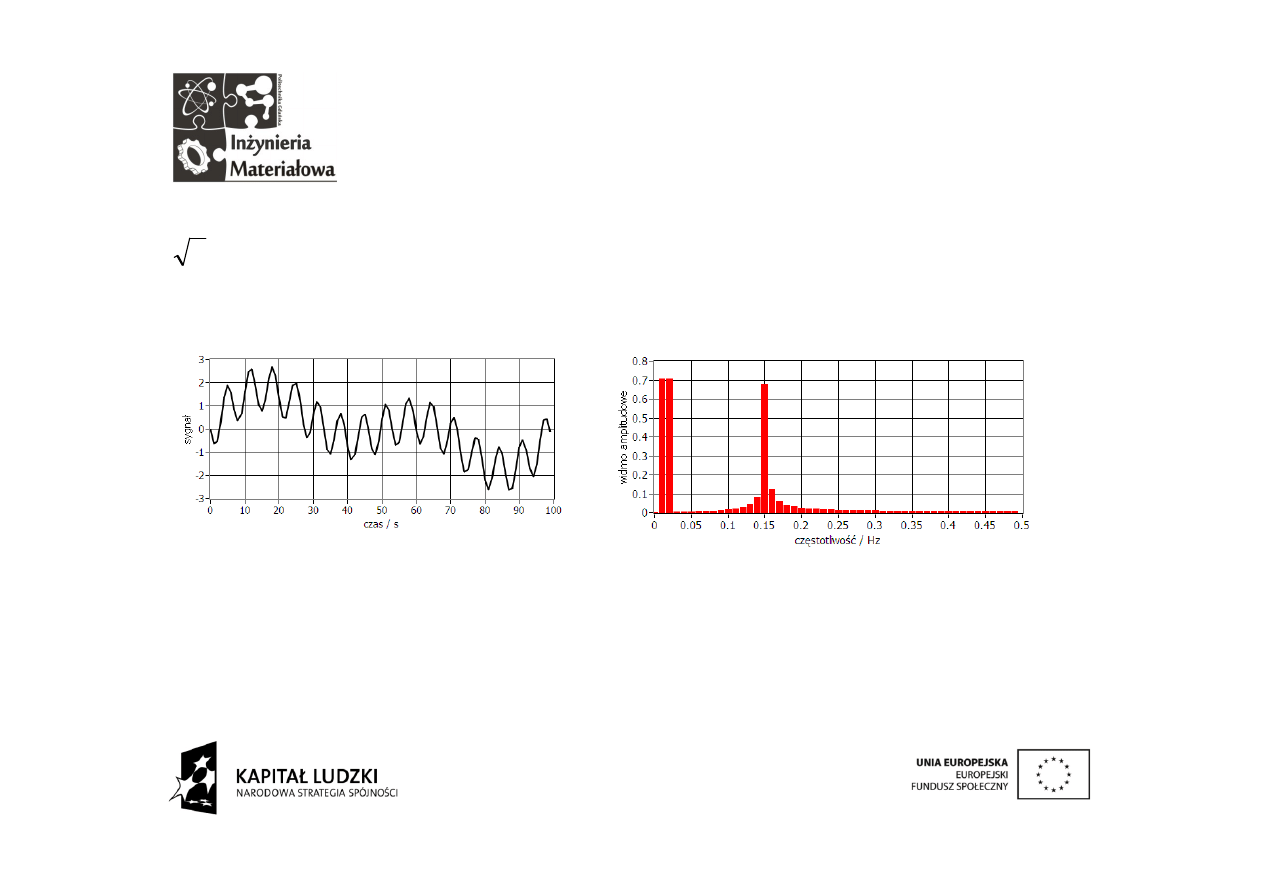
Teraz w miejsce składowej 0,6 Hz wprowadzamy składową o częstotliwości

. Zgodnie z założeniem podanym przy okazji omawiania budowy

szeregów trygonometrycznych taki sygnał

nie jest już okresowy. Po procesie

próbkowania sygnał i jego widmo wyglądają tak:

Jeszcze większy sabotaż

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Hz

2

6

,

0 ⋅

Niekiedy twierdzenie o próbkowaniu formułowane jest w sposób „przynajmniej
dwie próbki na okres sygnału”. Nie zawsze jednak można określić jaki jest okres.
Z tego względu lepiej jest mówić, że

częstotliwość próbkowania powinna być

dwa razy większa niż najwyższa częstotliwość składowej w widmie sygnału.

Dlaczego większa?

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

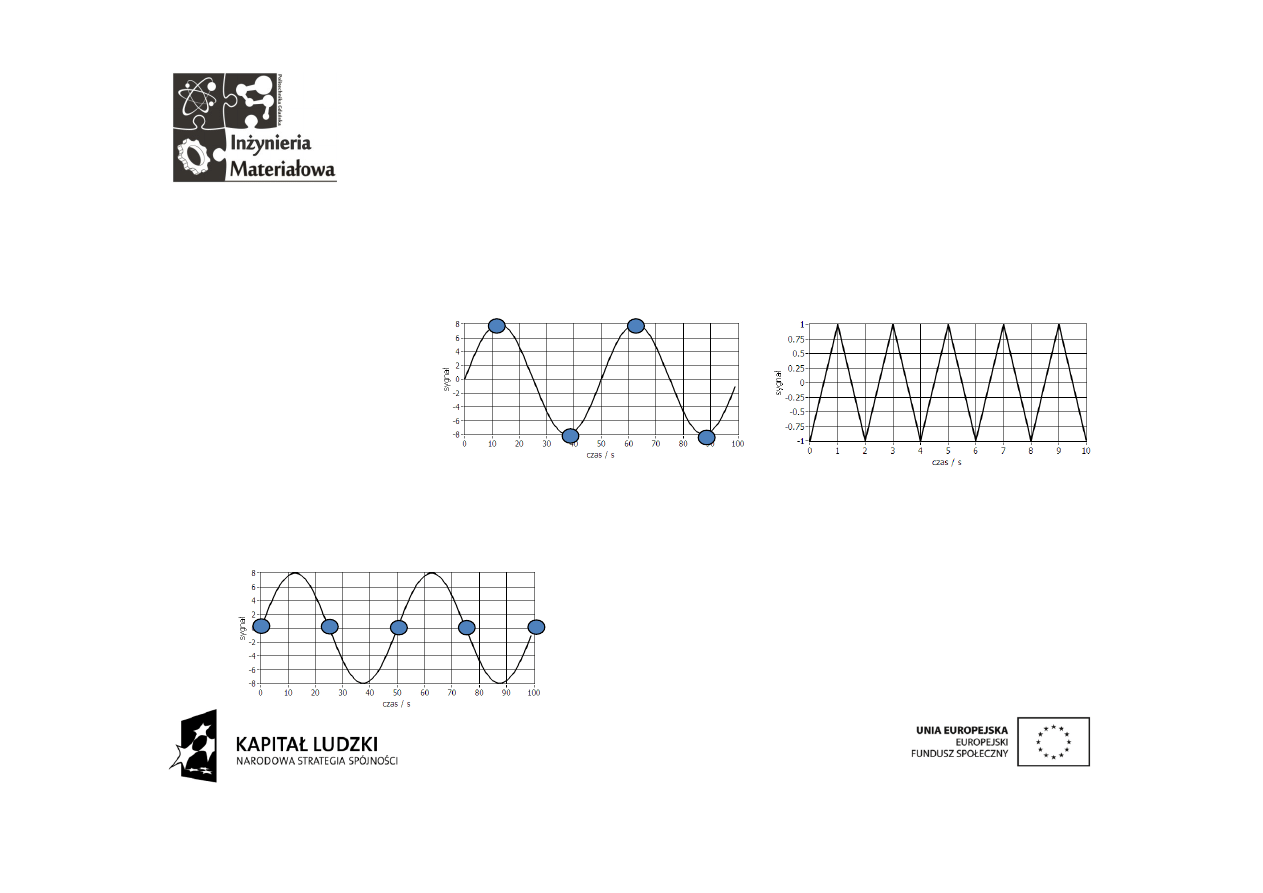
Dlaczego większa a nie większa bądź równa? Jeśli próbkujemy sygnał
okresowy z szybkością równą dwukrotności jego częstotliwości wszystko
powinno być w porządku:

Próbki zachowują strukturę częstotliwościową sygnału. Jeśli jednak
pechowo trafimy tak:

Otrzymamy same zera.

Różne widma

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

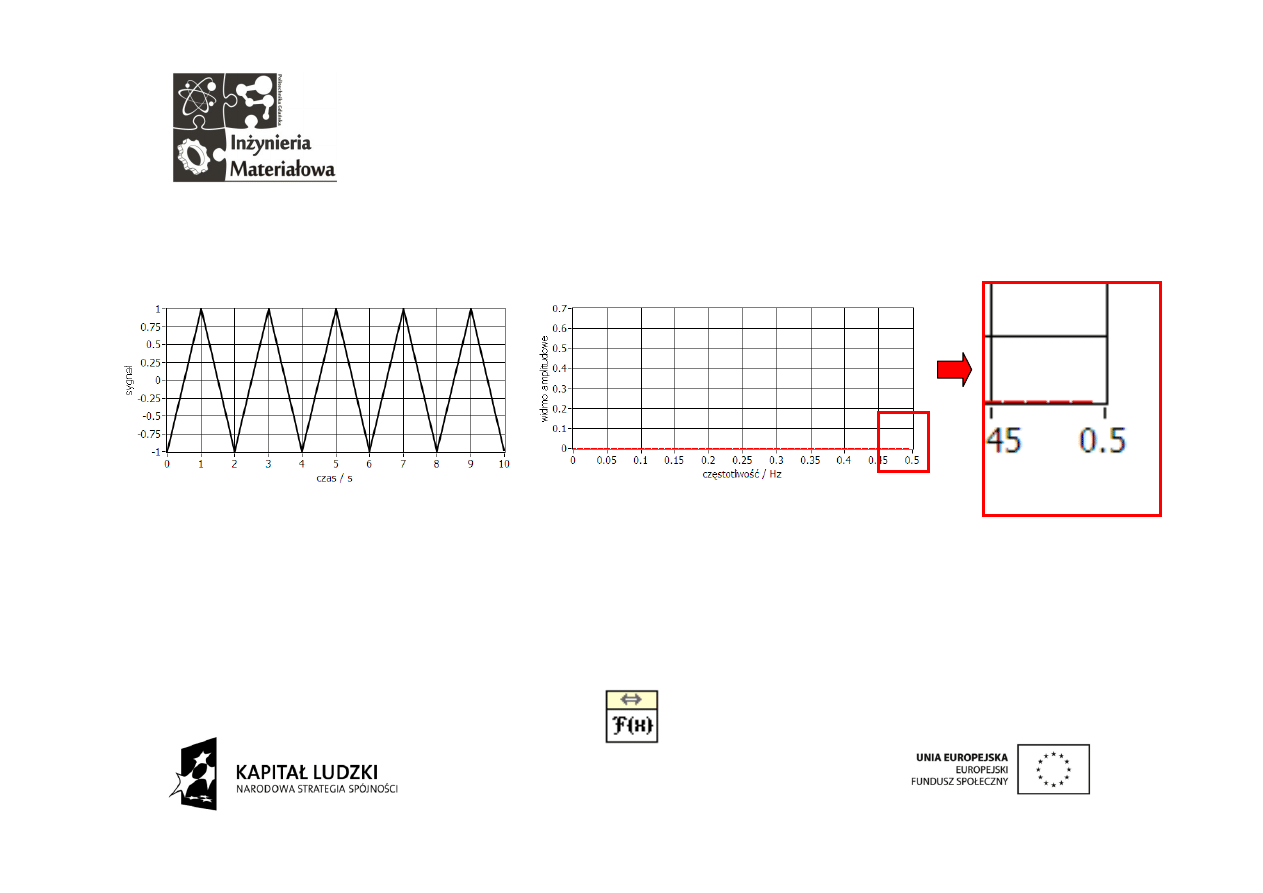
Procedura z LabVIEW znowu chroni nas przed tym ukrywając informację o
składowej widma przy połowie częstotliwości próbkowania:

Aby zobaczyć tę składową i obszary ukrywane przez procedurę należy
posłużyć się innym narzędziem, również dostępnym w LabVIEW ale
trudniejszym w obsłudze. Na palecie

„Signal Processing/Transforms”

znajduje się ikona oznaczona

„FFT”:

DFT i sinusoida

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

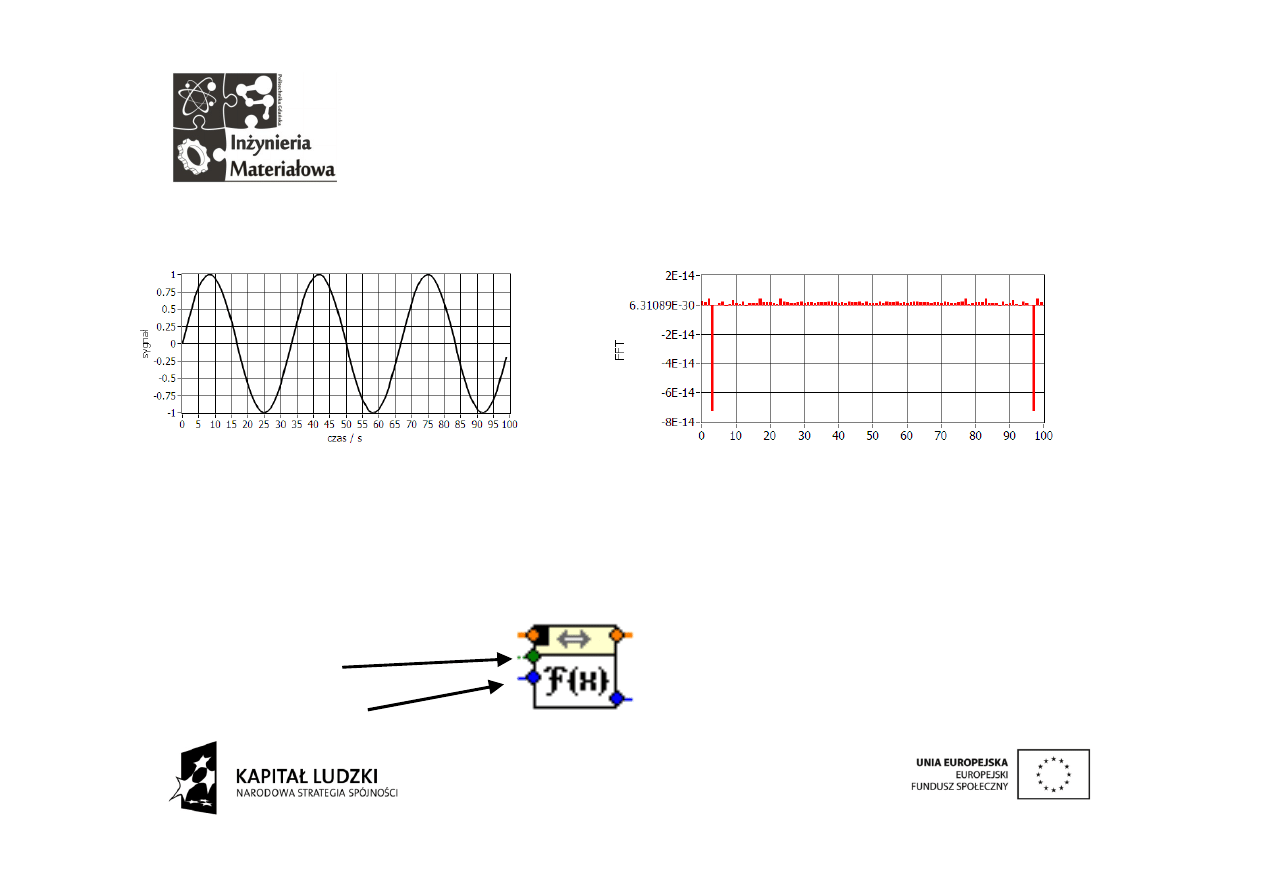
Zastosujmy DFT do analizy sygnału o poznanej strukturze widmowej aby
zobaczyć co właściwie robi nowo wprowadzona procedura

.

Otrzymujemy widmo zawierające prążki ale są one bardzo małe.
Dodatkowo skala widma jest zupełnie nieprzystająca do założeń. Struktura
połączeń

na schemacie pokazuje, że DFT nie produkuje skali

częstotliwościowej automatycznie.

sygnał wejściowy (x)

shift?

FFT size

FFT(x)

error

DFT to „ona”

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

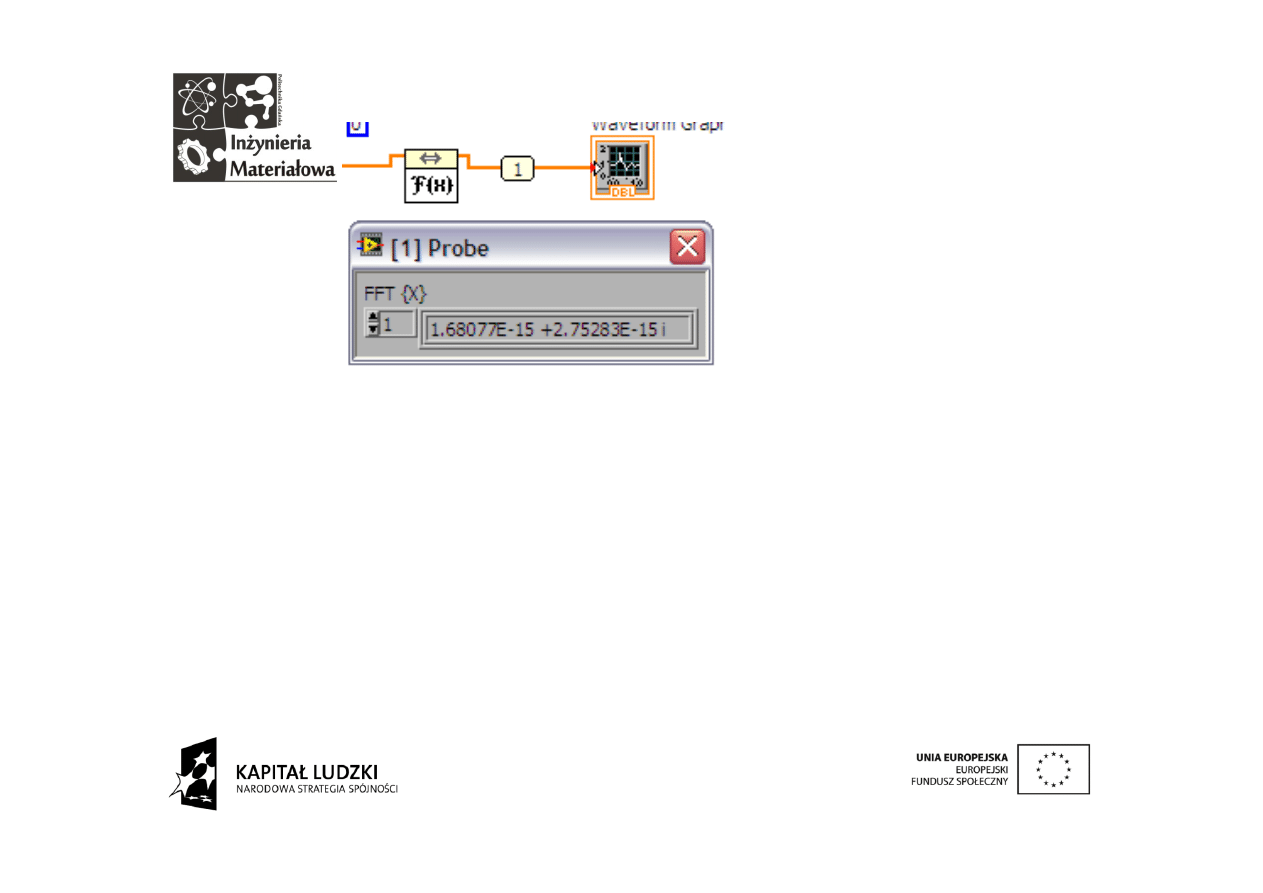
Zastosowanie próbnika na
przewodzie,

którym

przesyłana

jest

DFT

pozwala

zobaczyć,

ż

e

składa się ona z wartości
zespolonych.

Mówimy „ta” DFT ponieważ jak się wkrótce przekonamy jest to wynik działania
poznanego przez nas ostatnio dyskretnego przekształcenia Fouriera. Operacja
matematyczna nazywa się przekształceniem lub

transformacją natomiast jej wynik

to

transformata.

Widoczne jest, że transformata jest zespolona natomiast LabVIEW ma tą brzydką
cechę, że gdy próbuje się

narysować

wartości zespolone na wykresie

uwzględniana jest jedynie ich część rzeczywista. Rysunek z poprzedniego slajdu
jest zatem nieprawidłowy.
Na slajdach używane jest określenie DFT podczas gdy w LabVIEW nazwa FFT.
FFT to rozwinięcie od Fast Fourier Transformation, która stosuje bardziej wydajne
algorytmy.

Poprawny wykres DFT

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

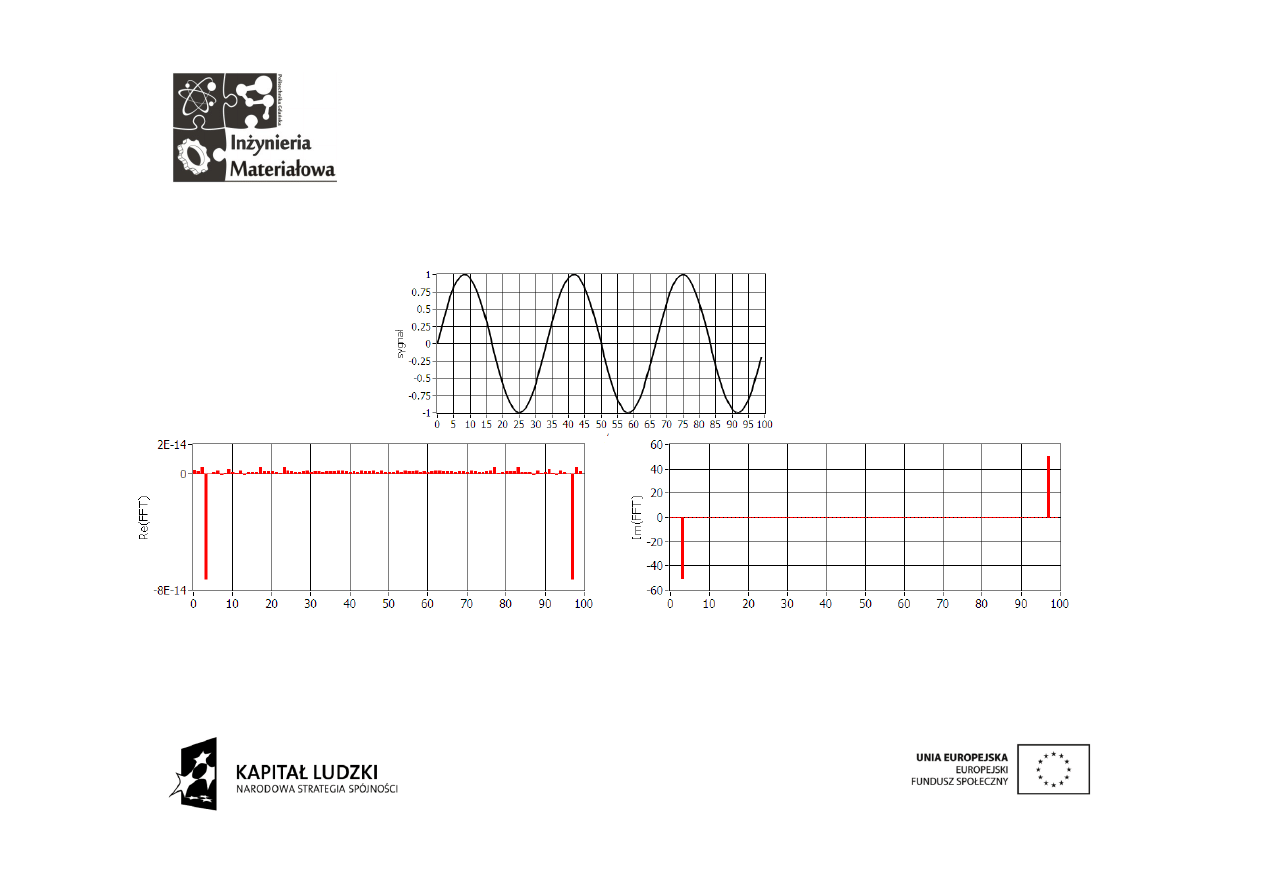
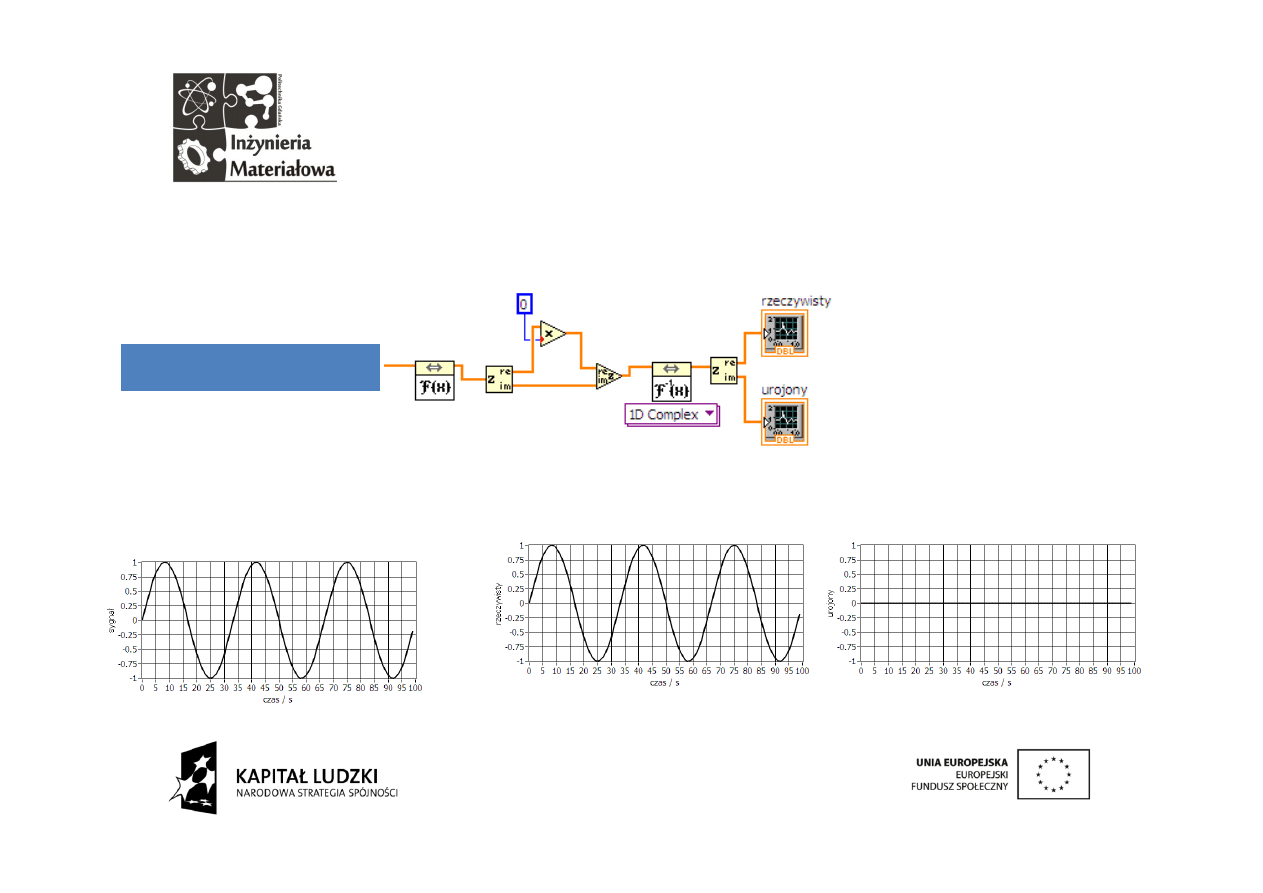
Na wykresach przedstawiona została część rzeczywista i urojona
analizowanego sygnału.

Część

rzeczywista

tej

transformaty

jest

pomijalnie mała.

Zasadnicza

informacja

zawarta jest w części
urojonej.

Odwracalność

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

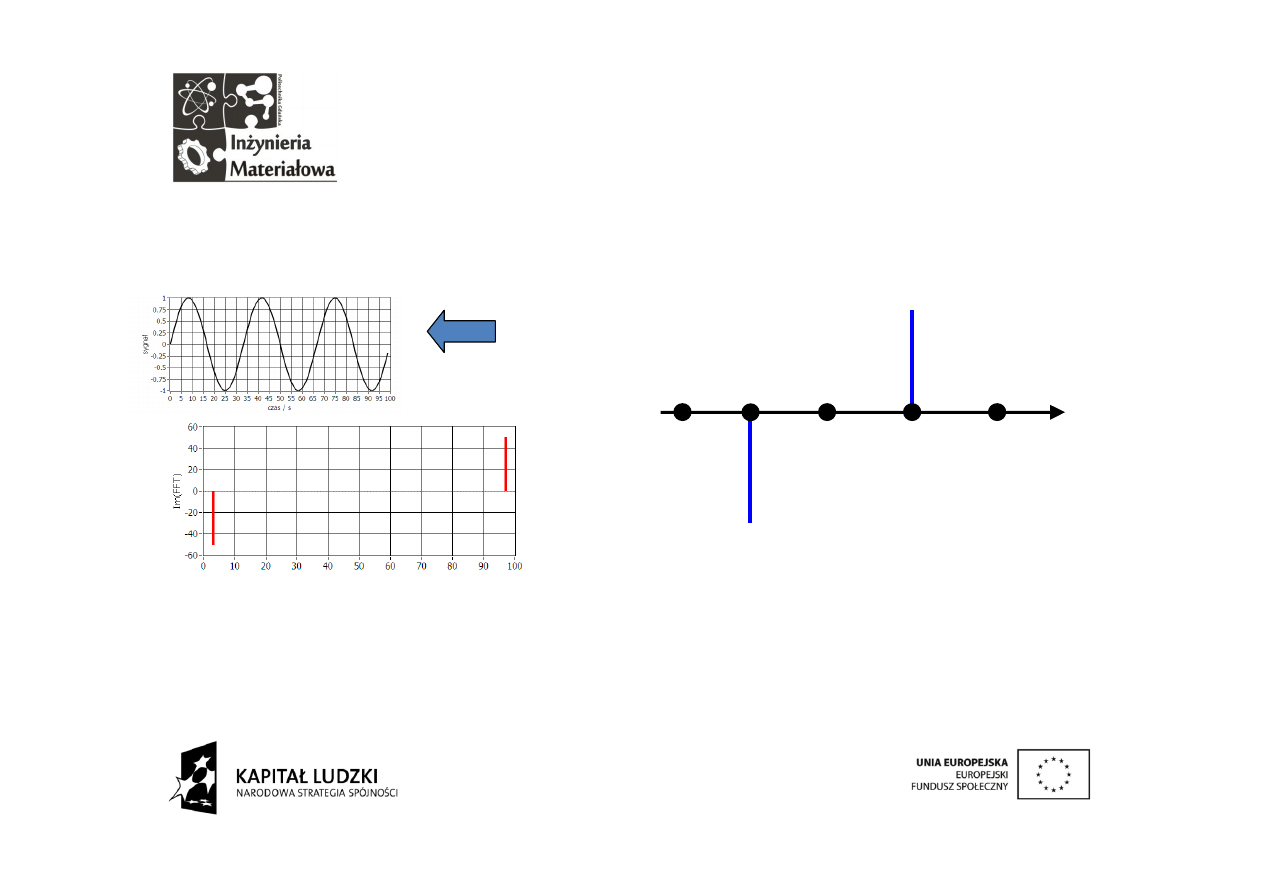
Operacja DFT jest odwracalna. Z zespolonych prążków można otrzymać sygnał
czasowy. Wykorzystamy to aby sprawdzić, że istotnie część rzeczywista ma w
omawianym przypadku znikome znaczenie.

Na przedstawionym schemacie dokonujemy całkowitego wyzerowania części
rzeczywistą

a następnie dokonujemy rekonstrukcji sygnału za pomocą

przekształcenia odwrotnego. Oto rezultat:

Sygnał wejściowy

Sygnał odtworzony

Sygnał wejściowy

Prążki DFT i krążenia

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

sygnał to sinus

Porównajmy postać wykresu prążkowego z wynikami graficznego
wyznaczania DFT z poprzedniego wykładu:

Widmo to dwa prążki jeden ma
ujemną wartość urojoną drugi
dodatnią ale również urojoną.

f

p

/4

f

p

3/4f

p

0

-2Ai

2Ai

Poprzednio dla sinusa również
wyszedł taki obraz. Ustaliliśmy,
ż

e do analizy 4 punktów

sygnału potrzebne były 4
wektory analizujące.

Rozdzielczość częstotliwościowa

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

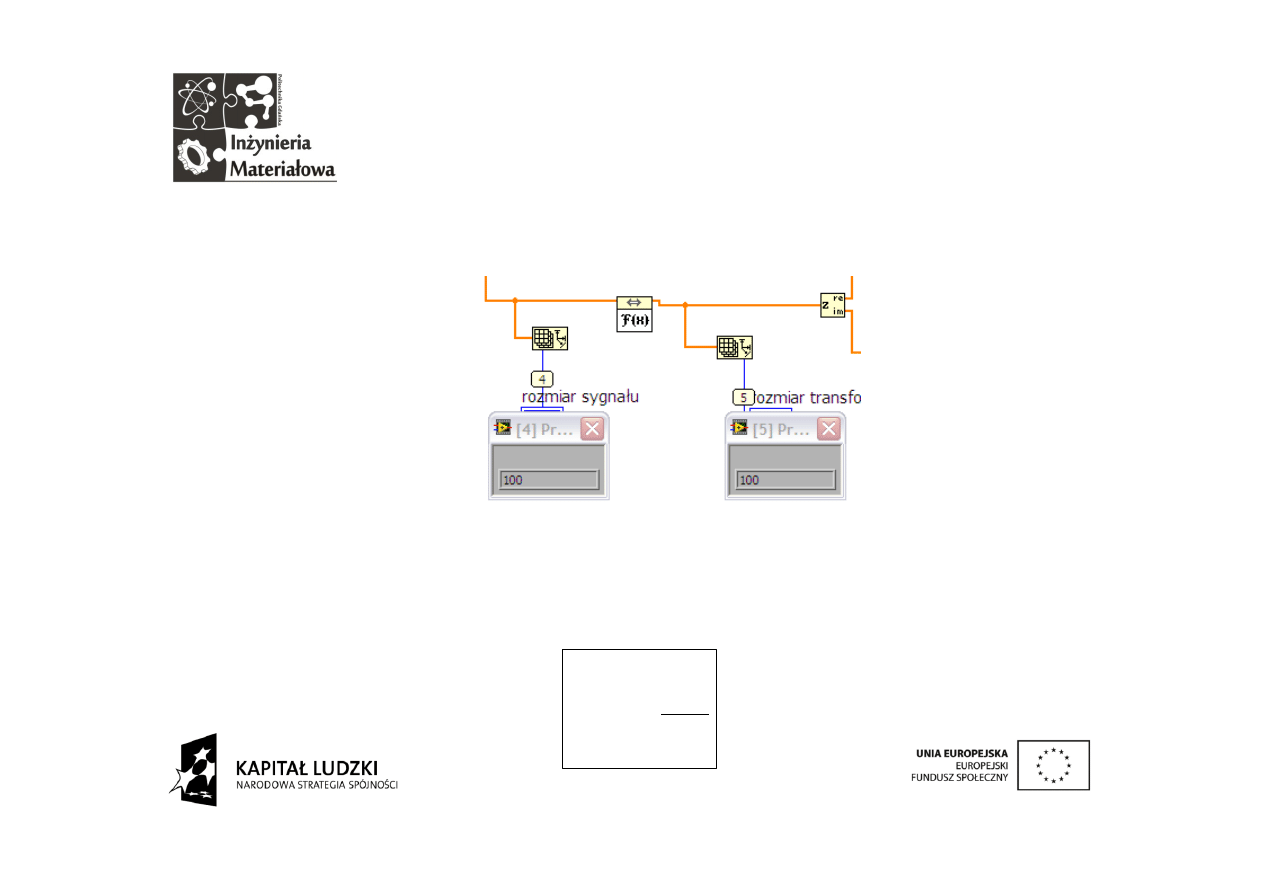
Sprawdzenie za pomocą próbnika pozwala przekonać się, że
procedura DFT wytwarza taką samą ilość próbek jaką miał
analizowany sygnał.

Przekonaliśmy się również że widmo sygnału cyfrowego posiada
okres równy f

p

zatem jeżeli transformata opisuje widmo sygnału

przy użyciu N próbek rozdzielczość częstotliwościowa (odstęp
między prążkami) wynosi

N

f

f

p

=

∆

Oś częstotliwości

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

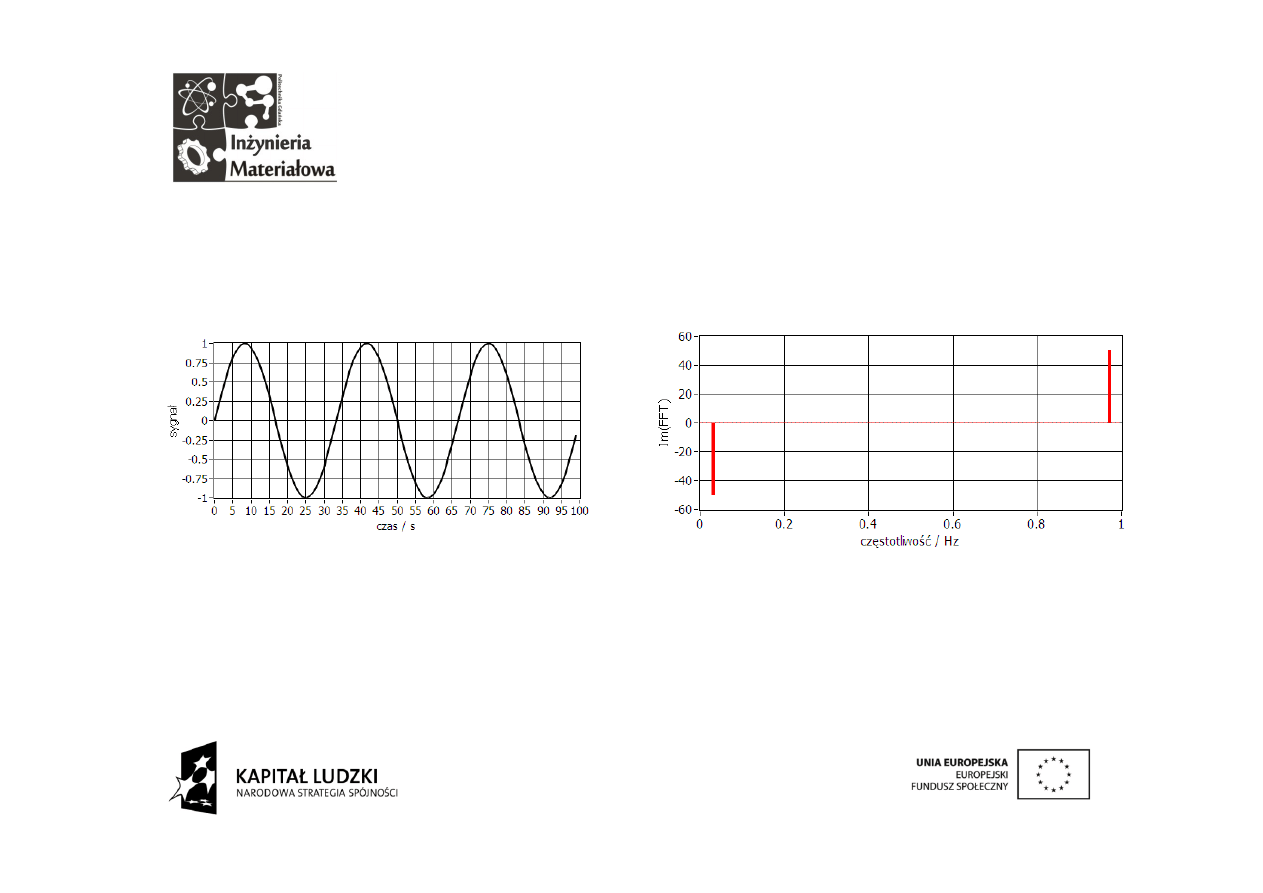
Przedstawiony wzór został wzięty w ramkę ponieważ jego
znaczenie jest ważne dla poprawnego wyskalowania osi odciętych
uzyskanej transformaty DFT.

Teraz można z czystym sumieniem podpisać oś odciętych
ponieważ pozwala ona odczytać prawdziwą częstotliwość sygnału.
Tak naprawdę na osi tej przedstawione są częstotliwości wektorów
analizujących.

Wektory analizujące…

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

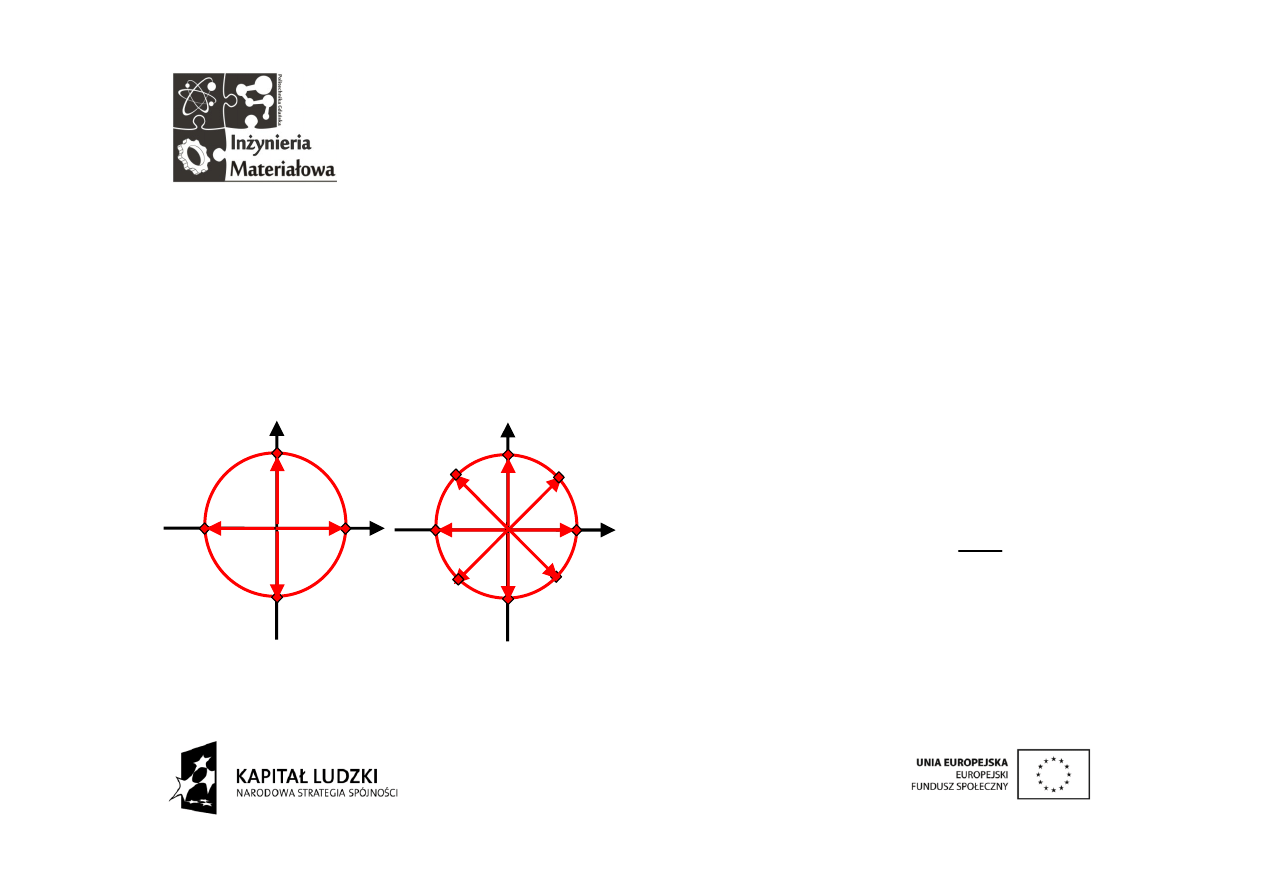
W przykładzie graficznym wykorzystaliśmy zbiór wektorów
analizujących w postaci zespolonej rozmieszczonych równomiernie
w zakresie od zera do częstotliwości próbkowania. Używaliśmy 4
wektorów a odległość między wektorami wynosiła fp/4. Była to
czteropunktowa dyskretna transformacja Fouriera. W ogólnym
przypadku używanych jest N wektorów.

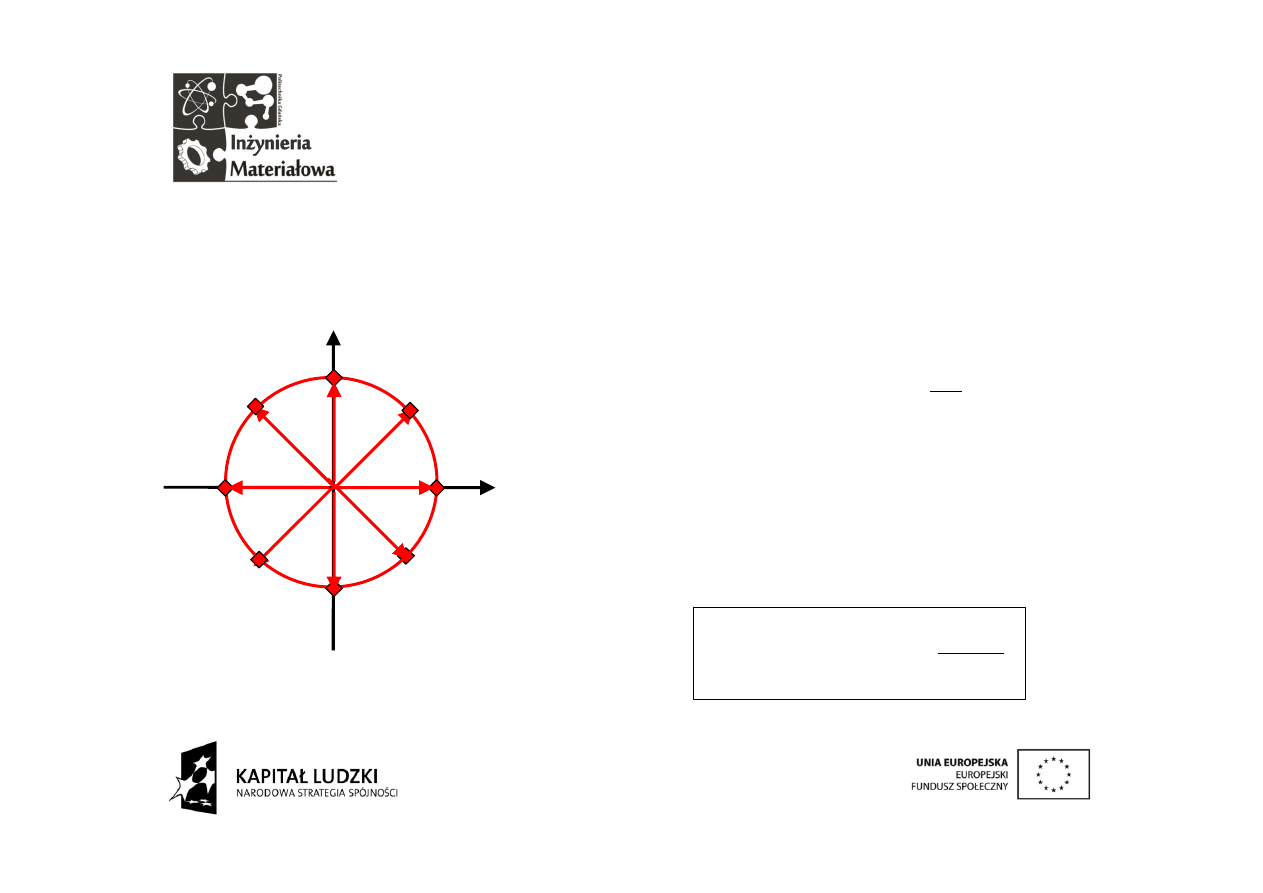
transformacja
4 punktowa

transformacja
8 punktowa

częstotliwości wektorów
określone są zależnością:

N

f

n

f

s

n

=

…i wzór na DFT

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

W rozważaniach rysunkowych kolejne prążki widma uzyskiwane
były poprzez sumowania iloczynów próbek sygnału z kolejnymi
położeniami sprzężonych wektorów analizujących.

pojedynczy wektor
analizujący

(

)

N

t

n

f

j

t

s

s

/

2

exp

)

(

∆

−

∆

π

(

)

N

n

f

j

s

s

/

0

2

exp

)

0

(

π

−

[

]

(

)

N

t

n

f

j

t

s

s

/

2

2

exp

2

∆

−

∆

π

biorąc pod uwagę, że:

s

f

t

1

=

∆

transformata stanowi n
próbek

w

dziedzinie

częstotliwości

o

wartościach:

[ ]

∑

=













−

=

N

k

n

N

kn

k

s

S

0

2

exp

π

Przekształcenie odwrotne

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

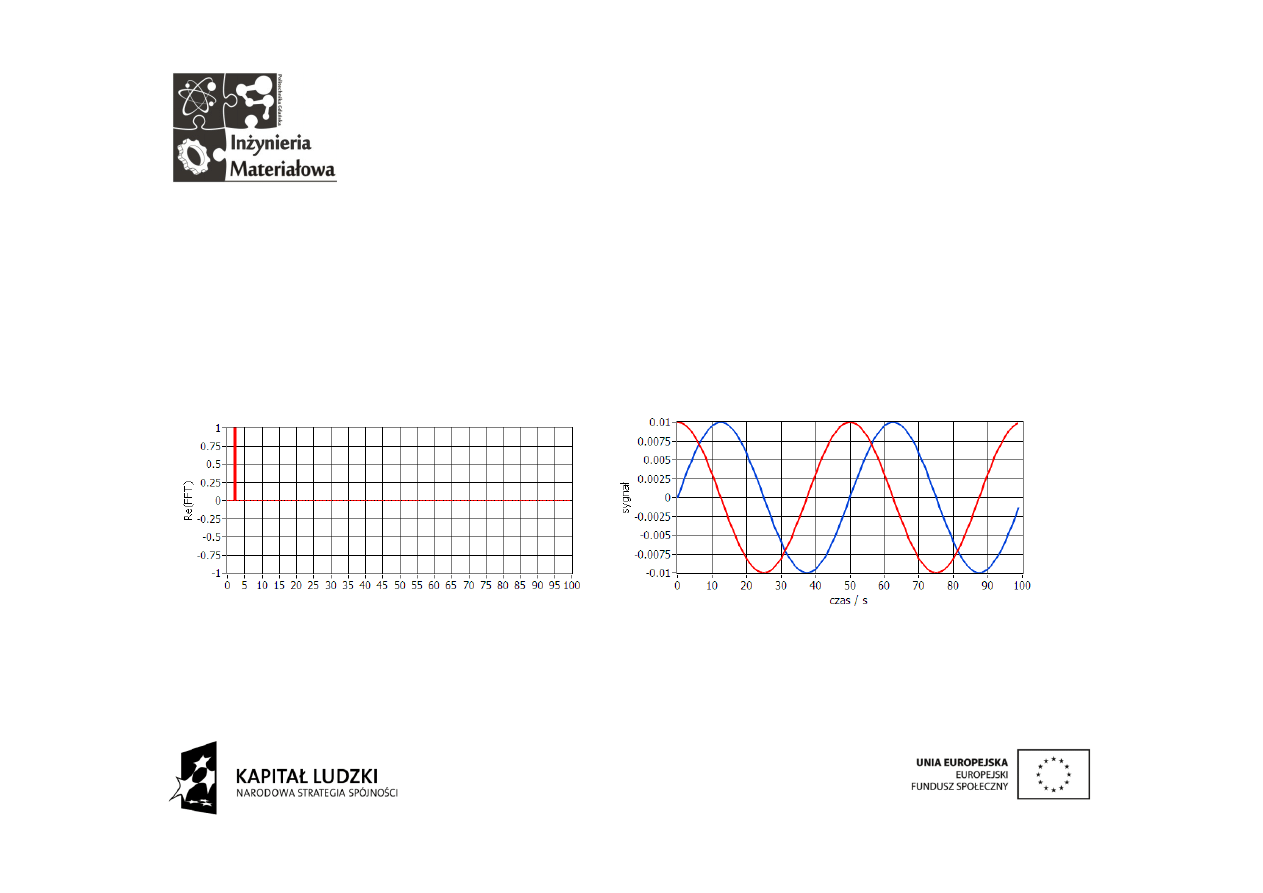
Skoro każdy prążek częstotliwościowy reprezentuje jedno krążenie
w przestrzeni zespolonej możliwe jest poustawianie odpowiednich
wartości prążków tak aby po transformacji odwrotnej otrzymać
żą

dany sygnał. Ustawiamy jednostkową wartość prążka składowej

rzeczywistej transformaty:

Otrzymujemy przebieg czasowy o charakterze zespolonym. Zgadza
się to z zależnością Eulera.

( )

( )

( )

x

x

i

ix

cos

sin

exp

+

=

Synteza sygnału rzeczywistego

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

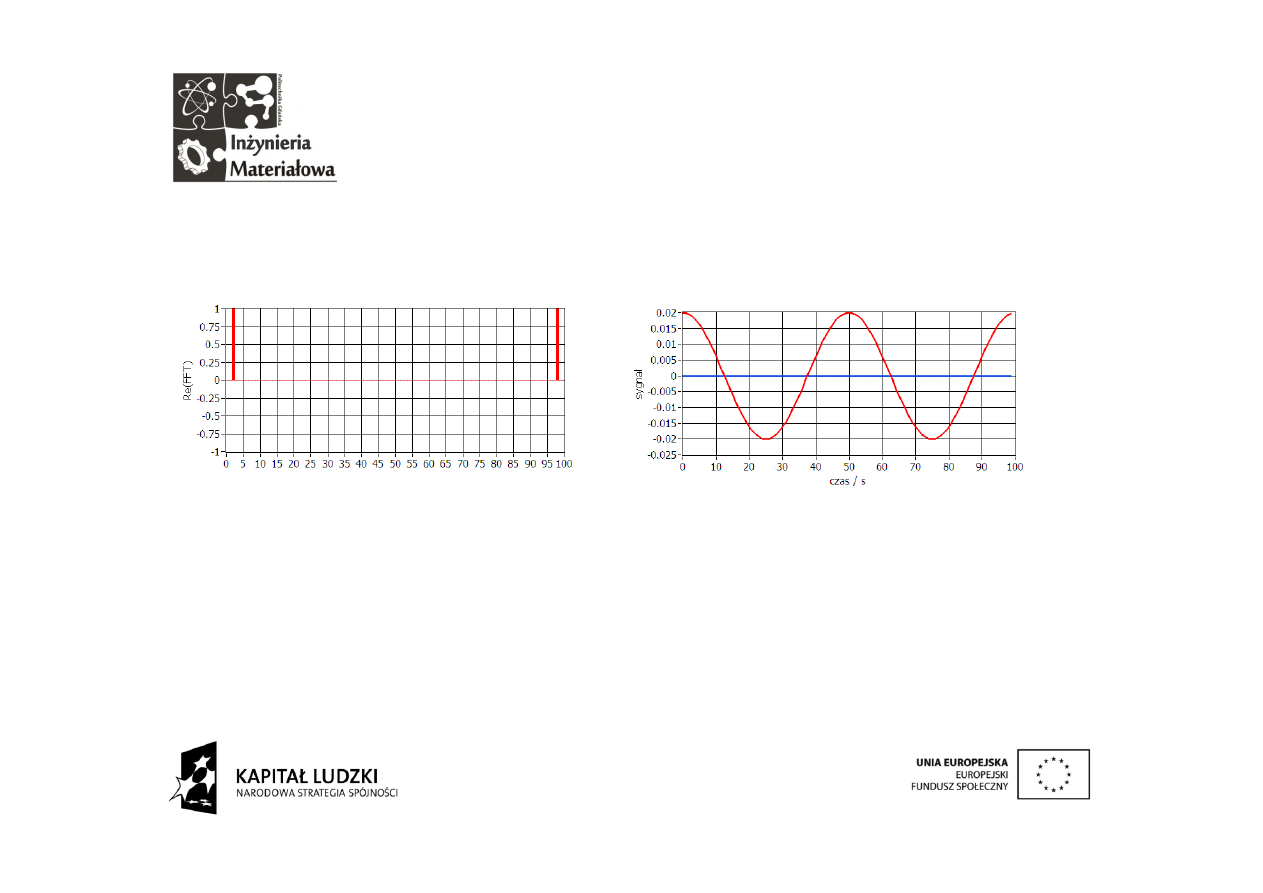
Aby stworzyć sygnał rzeczywisty należy dodatkowo ustawić
symetrycznie prążek o częstotliwości ujemnej.

W wyniku tej operacji otrzymujemy sygnał rzeczywisty będący
funkcją kosinus. W 100 punktowej transformacie ustawiony został
prążek numer 3 odpowiadający częstotliwości 0,02 Hz ponieważ
pierwszy prążek to częstotliwość

zero. Drugi odpowiada

częstotliwości 0,98 Hz. Jako że obowiązuje schemat powieleń
widma odpowiada to 0,02 Hz po ujemnej stronie częstotliwości.

Od DFT do widma

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

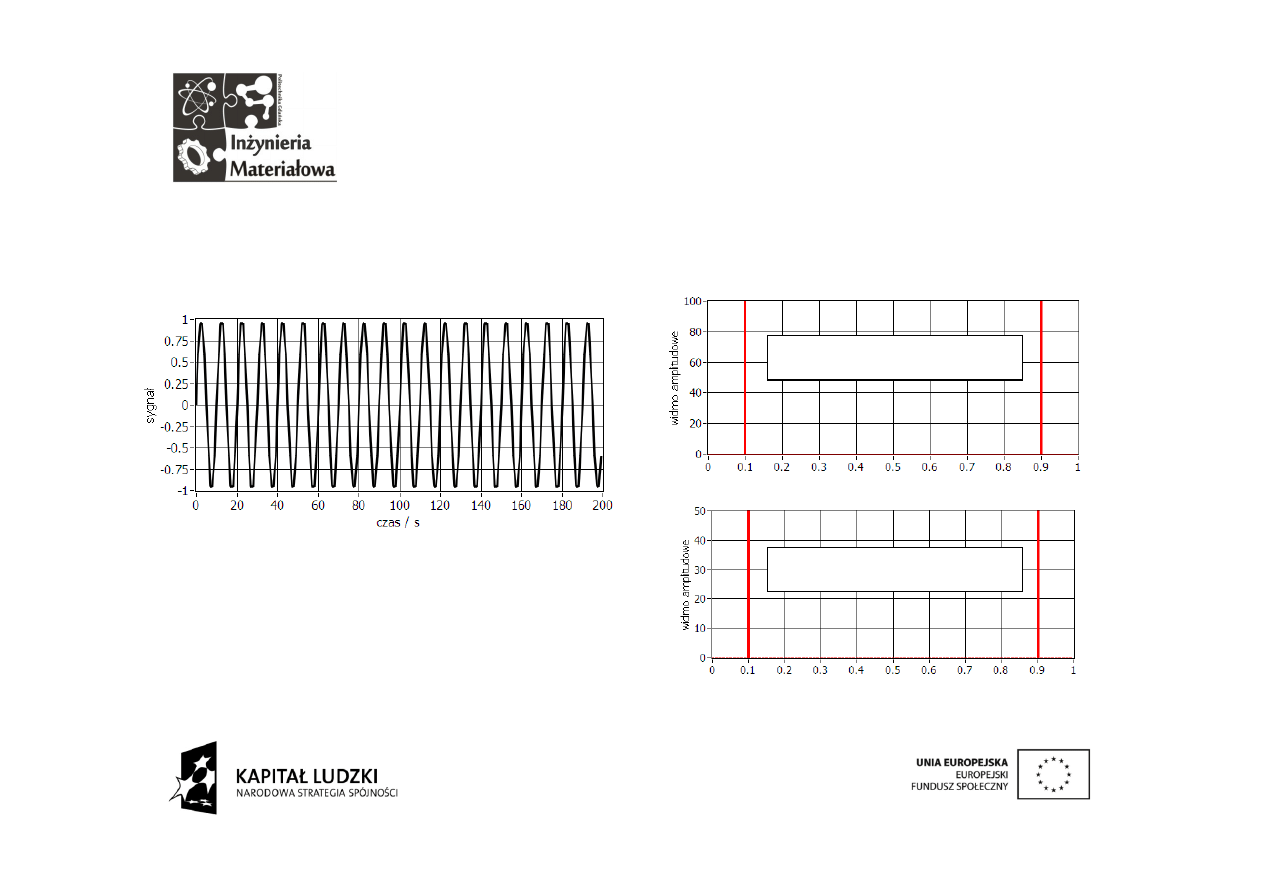
Transformata ma postać zespoloną. Często wygodnie posługiwać
się wartością jej modułu i fazy zamiast części rzeczywistej i
urojonej.

Otrzymany wynik jest zależny od
liczby próbek N. Z tego względu
stosuje się skalowanie przez 2/N
aby z widma odczytywać od razu
amplitudy

składowych

sinusoidalnych.

100 punktowa DFT

200 punktowa DFT

Podsumowanie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Przedstawione zostało powiązanie pomiędzy rozważaniami
teoretycznymi dotyczącymi strukturą

widma a rezultatami

otrzymywanymi za pomocą oprogramowania do analizy cyfrowej.
Algorytm DFT może być z powodzeniem użyty do dekompozycji
częstotliwościowej sygnałów dyskretnych.
Istnieje procedura odwrotna umożliwiająca syntezę sygnału w
oparciu o jego transformatę.

Kolejne zagadnienie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Warsztatem pracy, w którym wykonywane były wszystkie
dotychczasowe operacje związane z przetwarzaniem sygnałów
było LabVIEW. Pomimo niewątpliwych zalet takich jak relatywnie
duża intuicyjność, czy łatwość tworzenia interfejsu użytkownika
pakiet ten posiada niewątpliwą wadę. Jest drogi. Z tego powodu
następny

wykład

przybliży

możliwości

wykorzystania

oprogramowania dostępnego legalnie i za darmo w sieci.