Dużo rysunków mało

rachunków

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Podobnie jak przedstawione uprzednio wzory całkowe służą do
rozkładania budowli złożonych z funkcji ciągłych na elementarne
cegły funkcji trygonometrycznych tak samo możliwe jest rozbijanie
przebiegów dyskretnych. Operatory całkowe posiadały czynniki o
zmieniającej się częstotliwości. Wykorzystując technikę przestrzeni
zespolonej zobaczymy, że wektory o różnej szybkości wirowania
pełnią taką samą funkcję. Zrobimy to wykorzystując prawie
wyłącznie obrazki.

Sygnał ciągły…

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Sygnał ciągły reprezentowany przez obieg w przestrzeni zespolonej
wiedzie swój wyjątkowo monotonny żywot, który składa się z kolejnych
okresów.

Każdemu przyrostowi czasu

∆

t

odpowiada

stały przyrost kąta

∆ ϕ

. W czasie równym

okresowi sygnał przebywa 2π. Szybkość
wirowania jest stała.

0

2

)

(

ϕ

π

ϕ

+

=

t

T

t

1

1

,

ϕ

t

2

2

,

ϕ

t

Sygnał

podglądany jest w określonych chwilach czasu

wyznaczanych przez częstotliwość próbkowania.

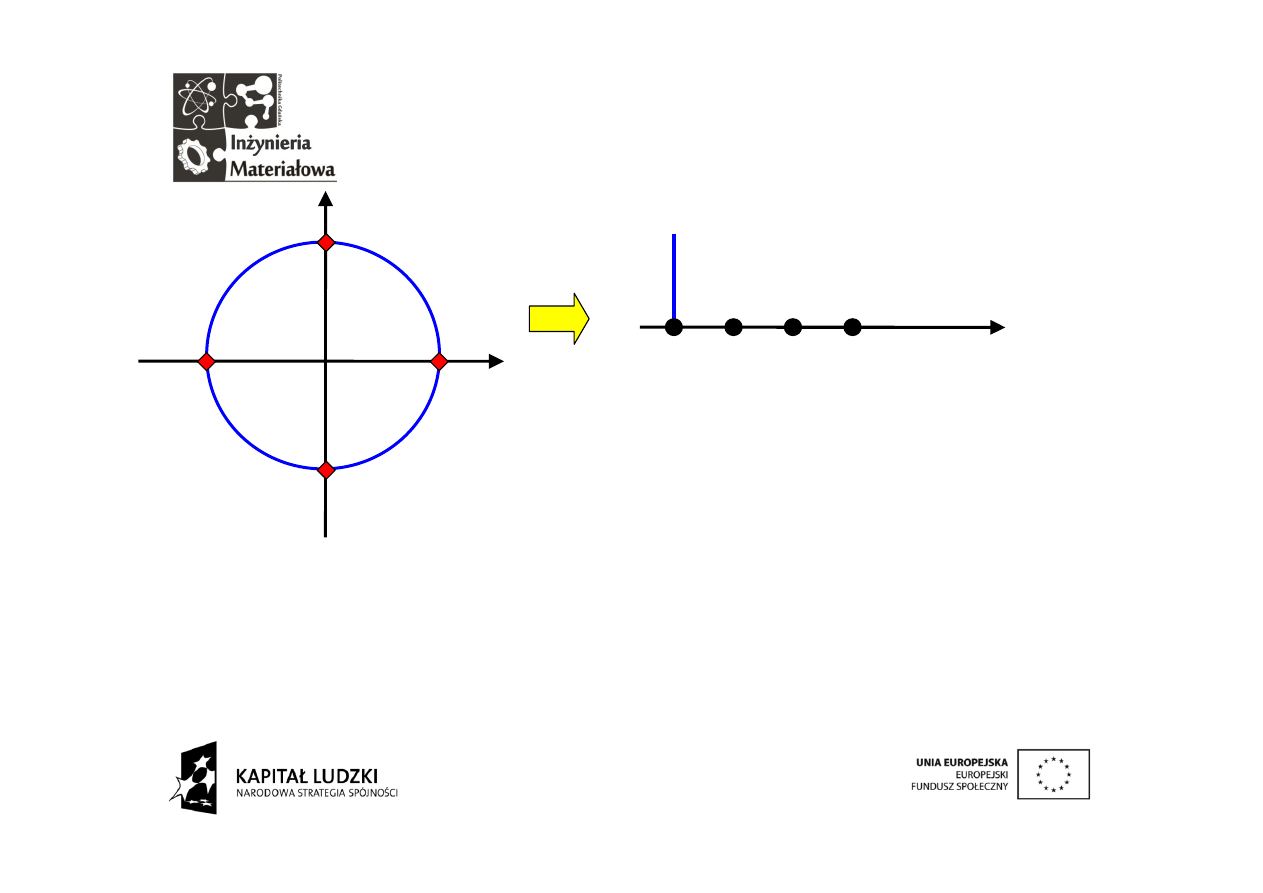
… i cyfrowy paparazzi

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

W

tym

przypadku

sygnał

„fotografowany” jest cztery razy w
ciągu swojego okresu. Częstotliwość
przebiegu analogowego może być
wyrażona względem częstotliwości
próbkowania.

f

p

/4

częstotliwość

Na

osi

częstotliwości

można

oznaczyć

częstotliwość próbkowania i
częstotliwość sygnału, która
jest 4 razy mniejsza.

f

p

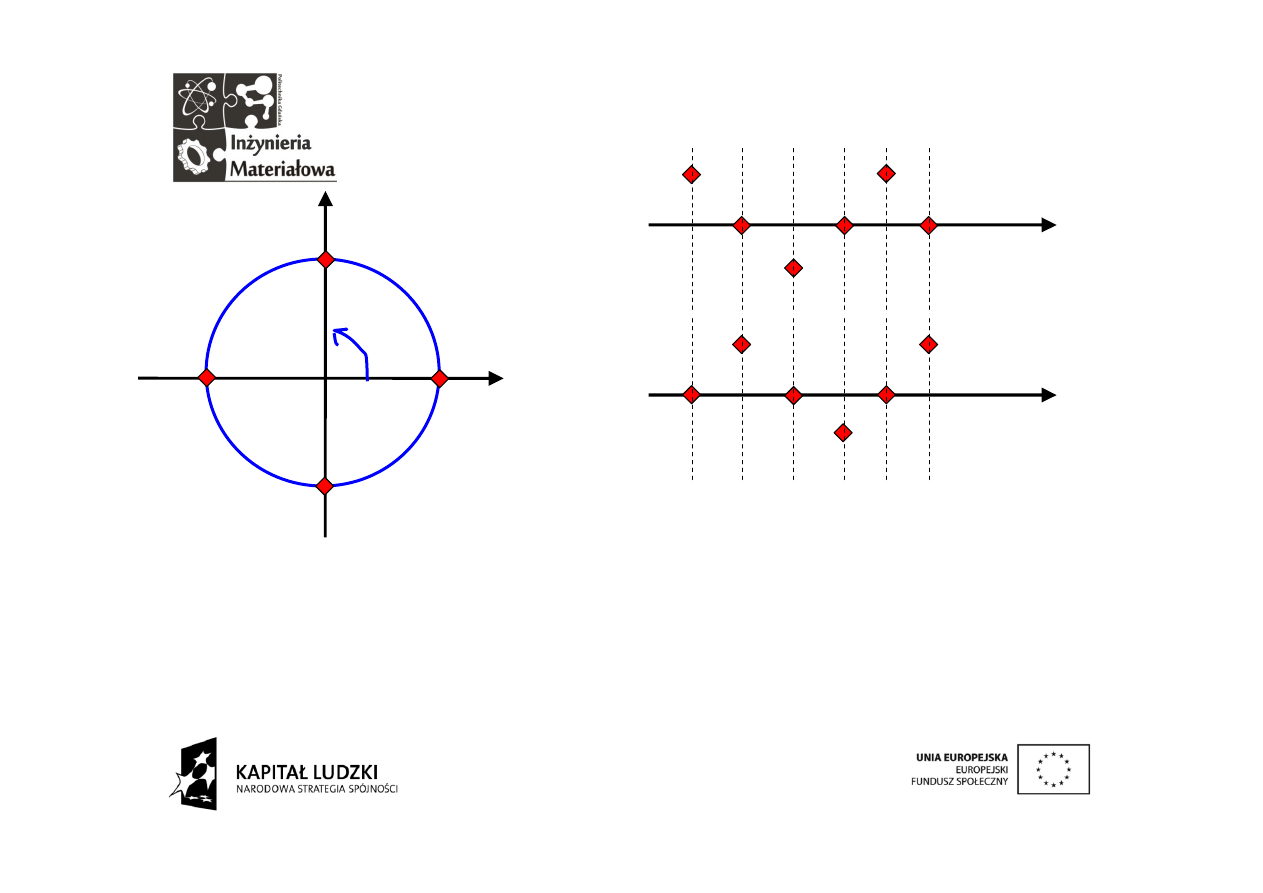
Widok na osi czasu

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

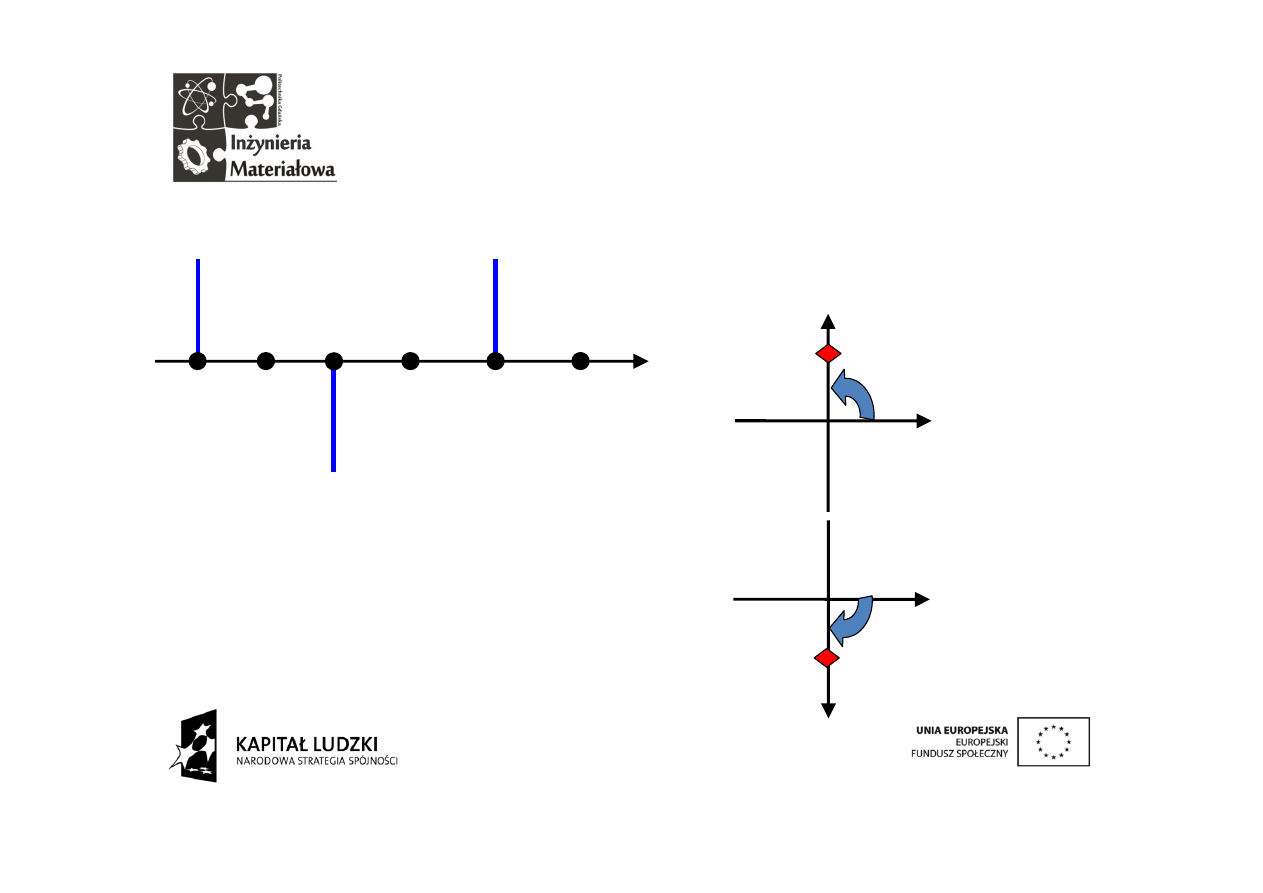
W

czasie

ć

wierci

okresu

próbkowania sygnał obraca się
o π/2. „A” to amplituda sygnału
a czerwone punkty oznaczają
jego chwilowe wartości.

Wzajemna

relacja

częstotliwości

próbkowania i częstotliwości sygnału
próbkowanego w tym przykładzie zostały
tendencyjnie dobrane w taki sposób aby
łatwo było określić wartości próbek i
narysować je na osi czasu.

czas

czas

c

z

ę

ś

ć

rz

e

c

z

y

w

is

ta

c

z

ę

ś

ć

u

ro

jo

n

a

A

Ai

-A

-Ai

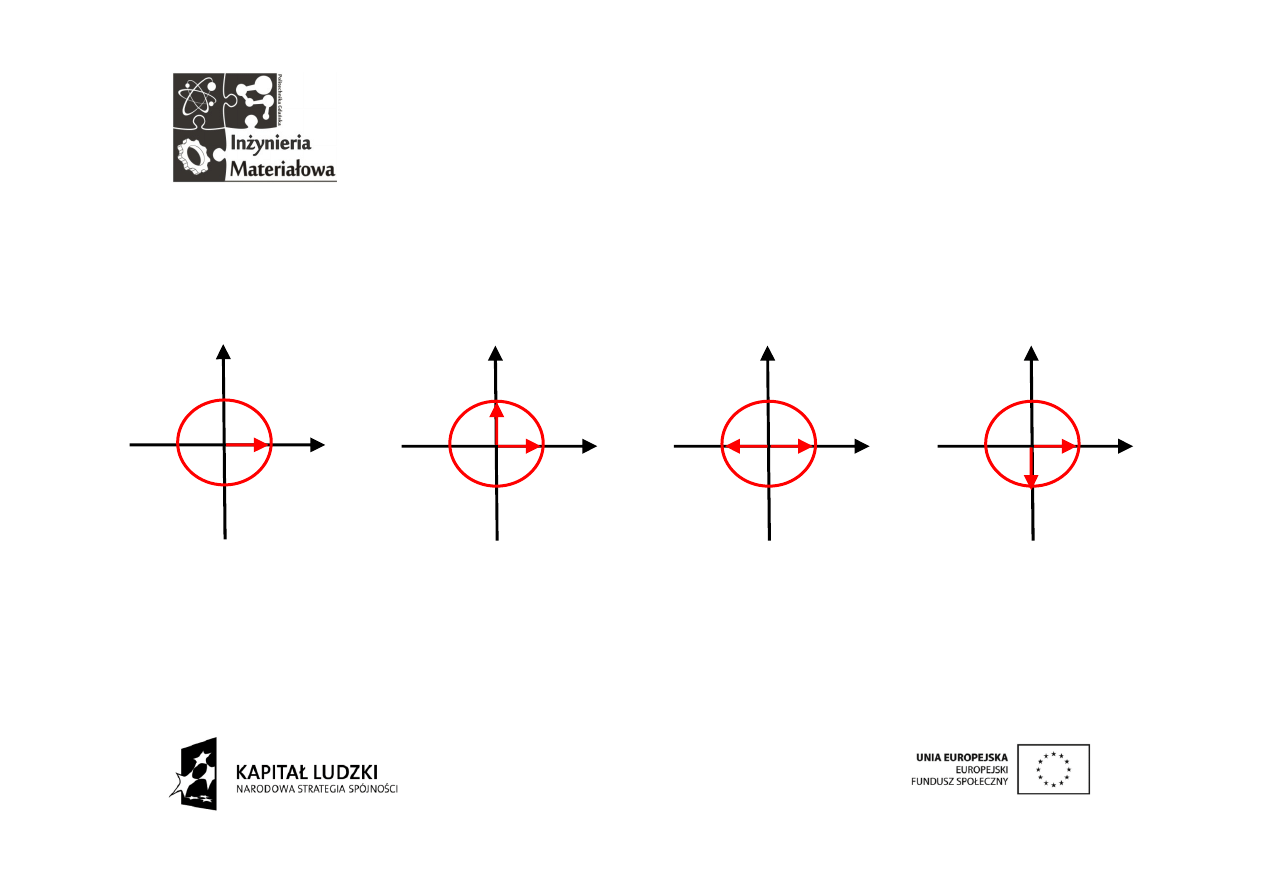
Zamiast całek wektory

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Przedstawiony sygnał poddany zostanie analizie podobnej do analizy
dotyczącej szeregu Fouriera. Podobnie jak poprzednio rozważania
dotyczyć będą jednego okresu. Tu jednak nie ma miejsca na całki. W ich
zastępstwie wystąpią wektory analizujące. Są one dyskretne zatem
przeskakują w różnym tempie między punktami próbkowania.

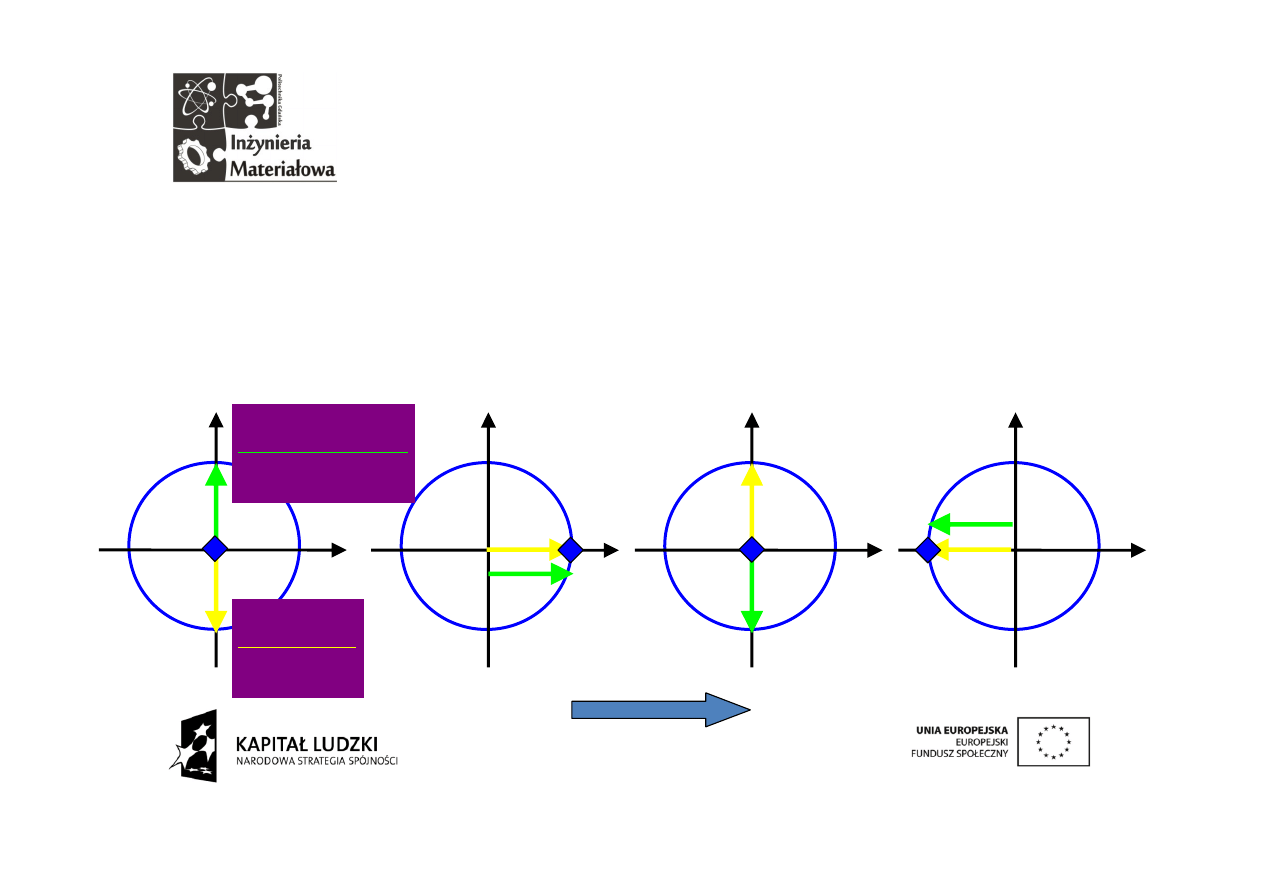
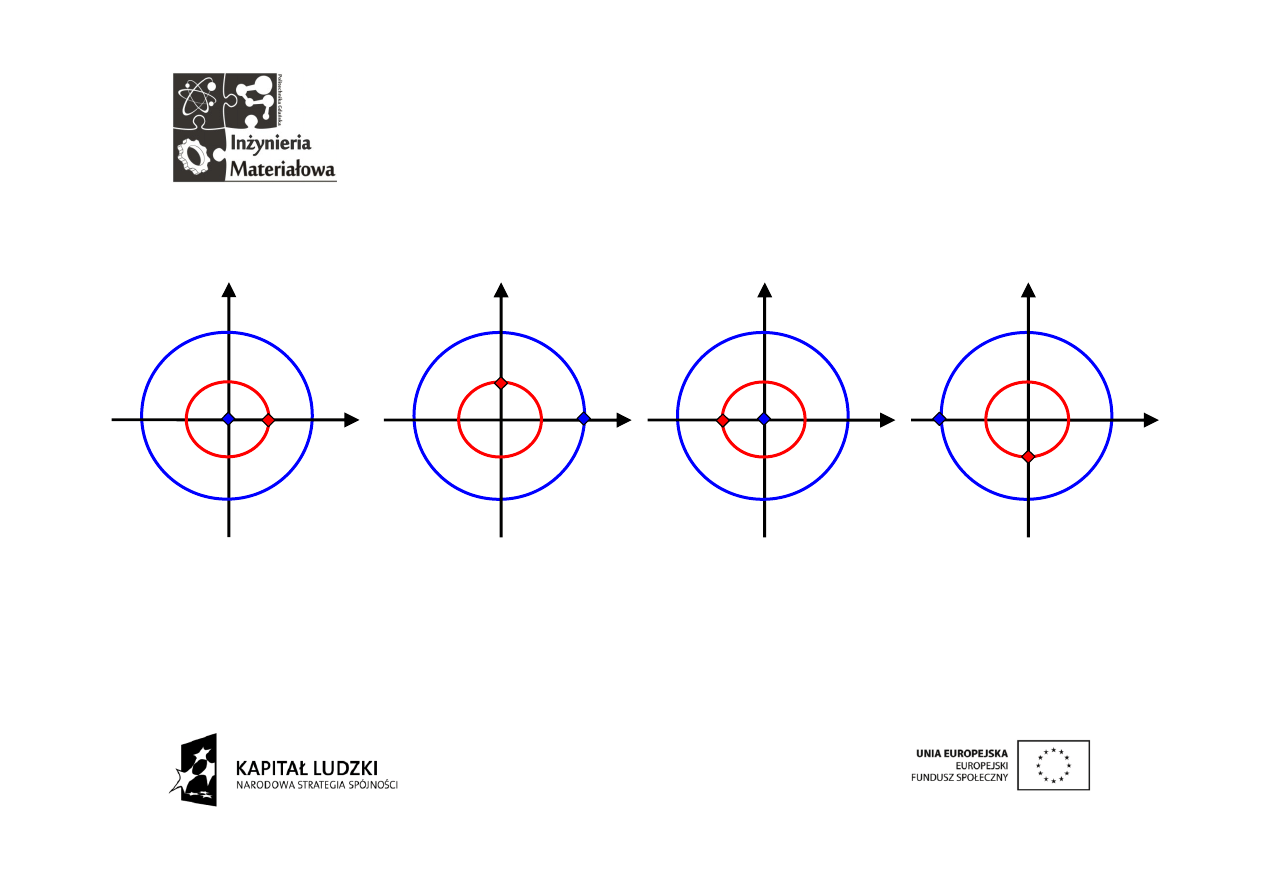
Drugi

wektor

w

ciągu

okresu

przeskakuje o π/2.

Konsekwentnie,
trzeci przeskoczy o
π,

a czwarty o 3/2 π.

Pierwszy wektor jest
nieruchomy.

Nie ma sensu wprowadzania piątego wektora bo jest on tym samym co
pierwszy. Wszystkie wektory mają taką samą długość równą 1.

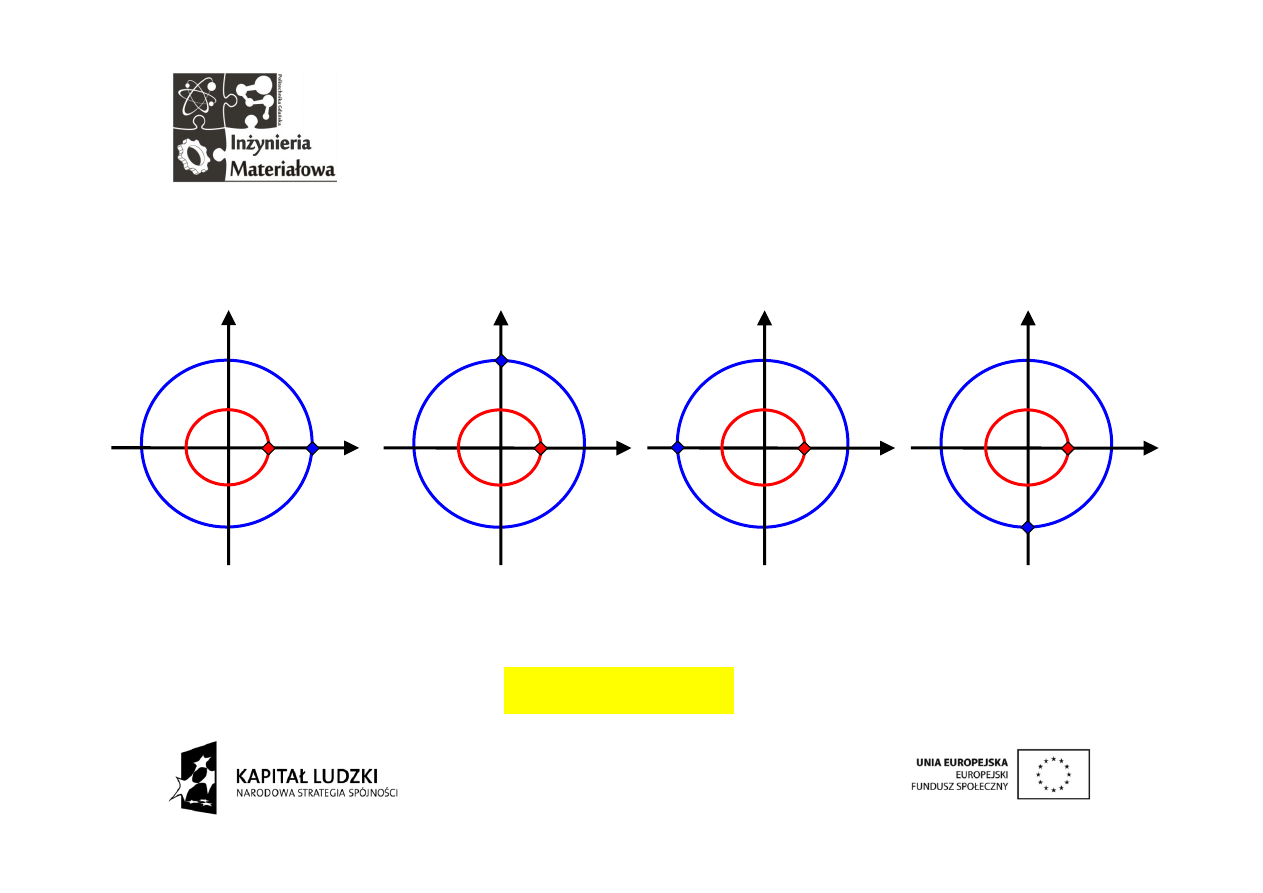
Cztery wektory i starcie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

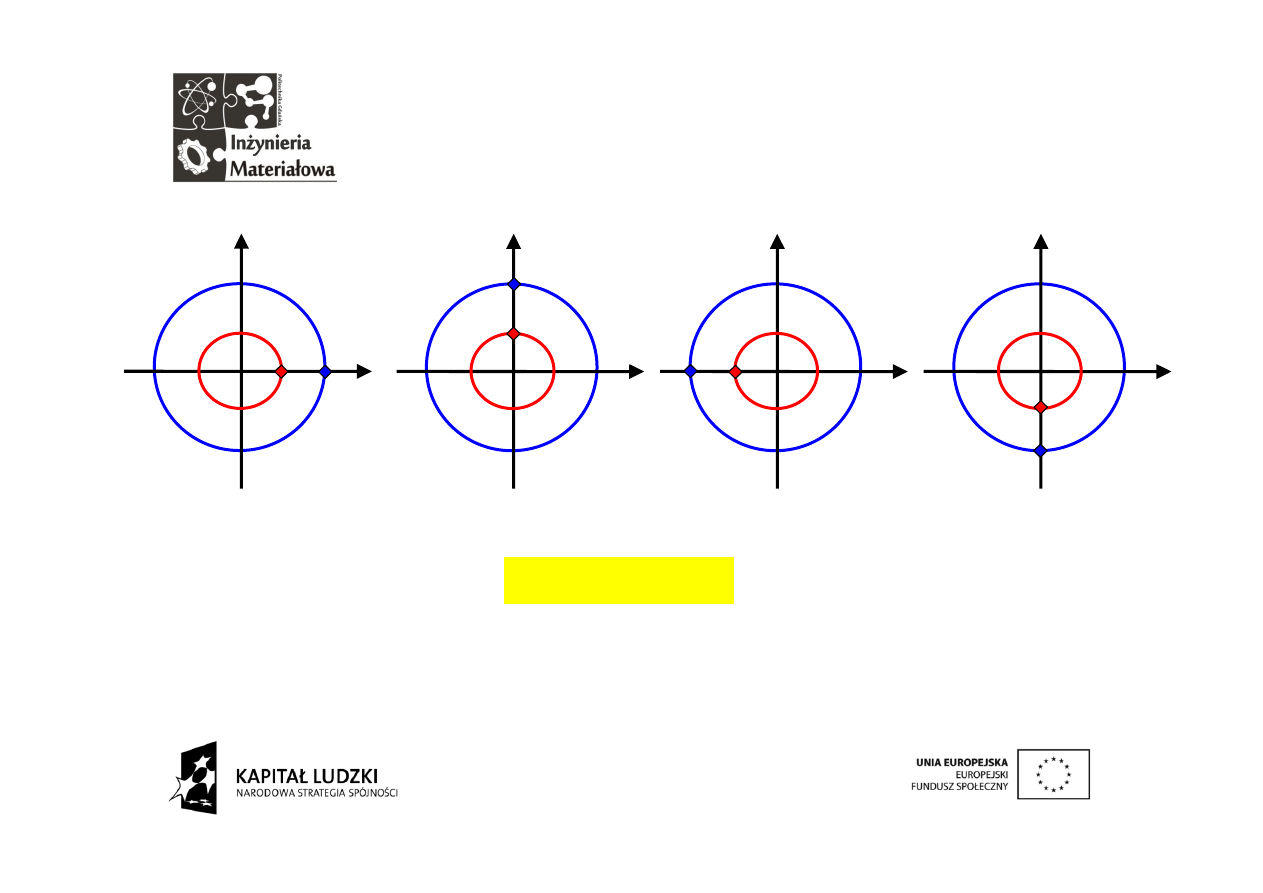
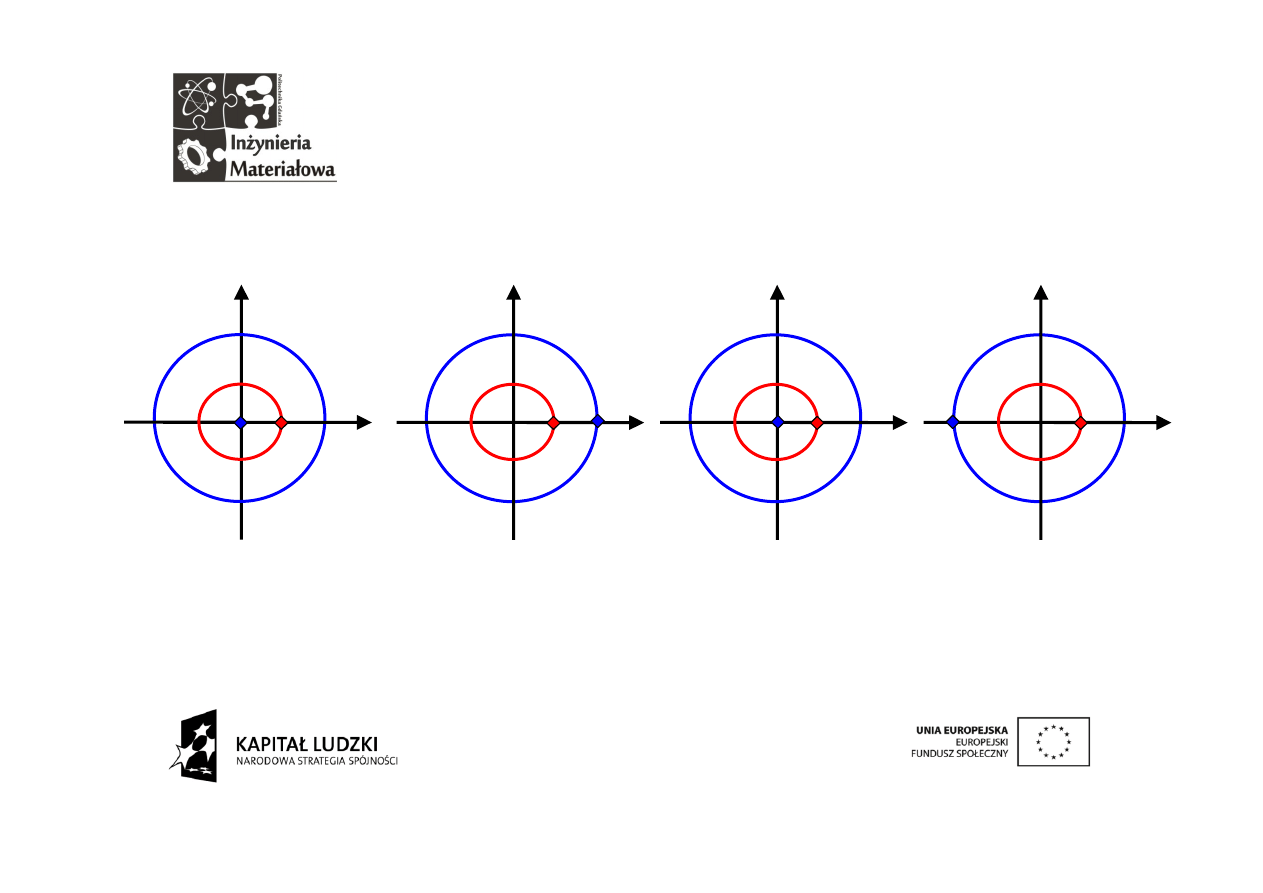
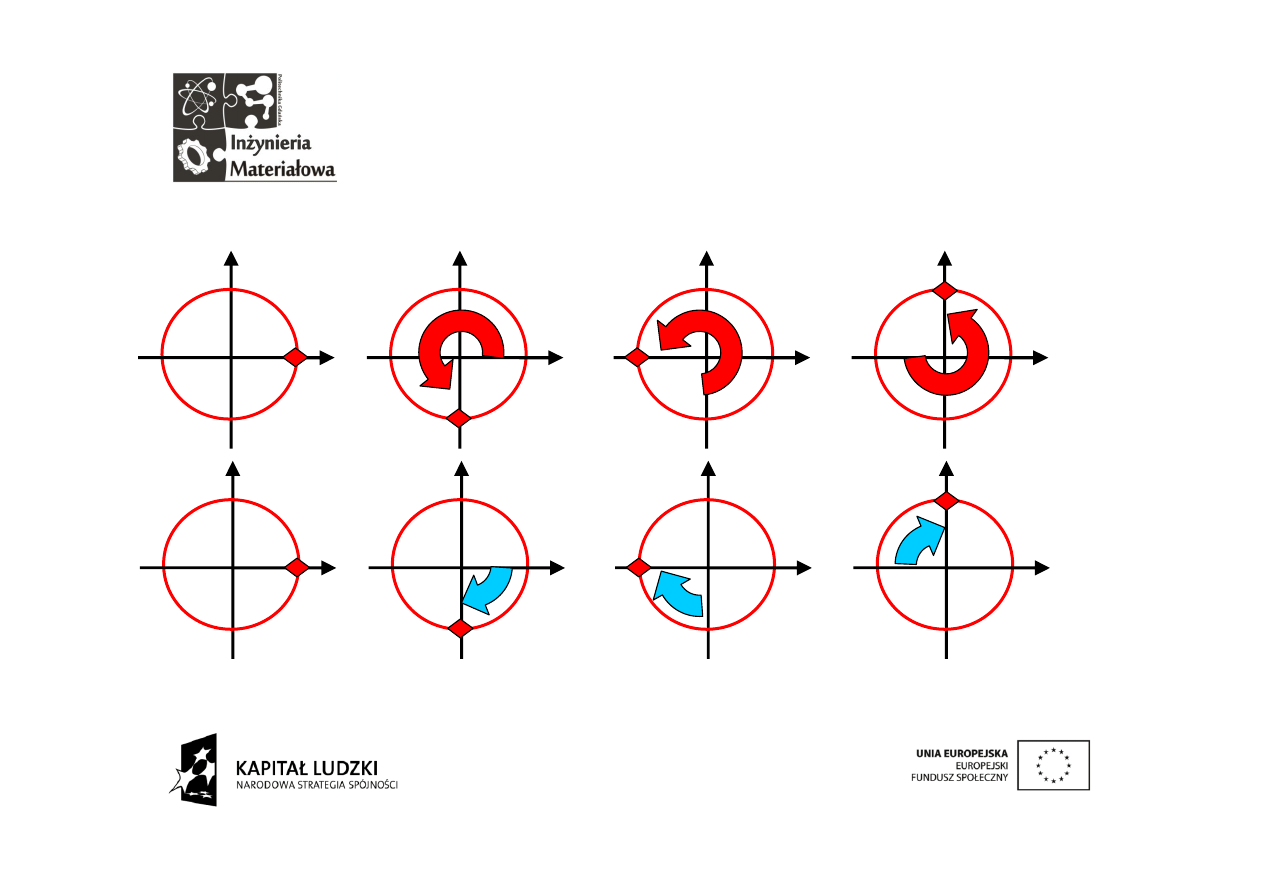
Teraz będziemy fotografować wzajemne położenia sygnału dyskretnego i
kolejnych wektorów. Najpierw wektor nieruchomy. Mnożymy położenia
sygnału (niebieskie) i wektora analizującego (czerwone).

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

iloczyn = A

iloczyn = Ai

iloczyn = -A

iloczyn = -Ai

Na koniec sumujemy otrzymane iloczyny:

suma = 0

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

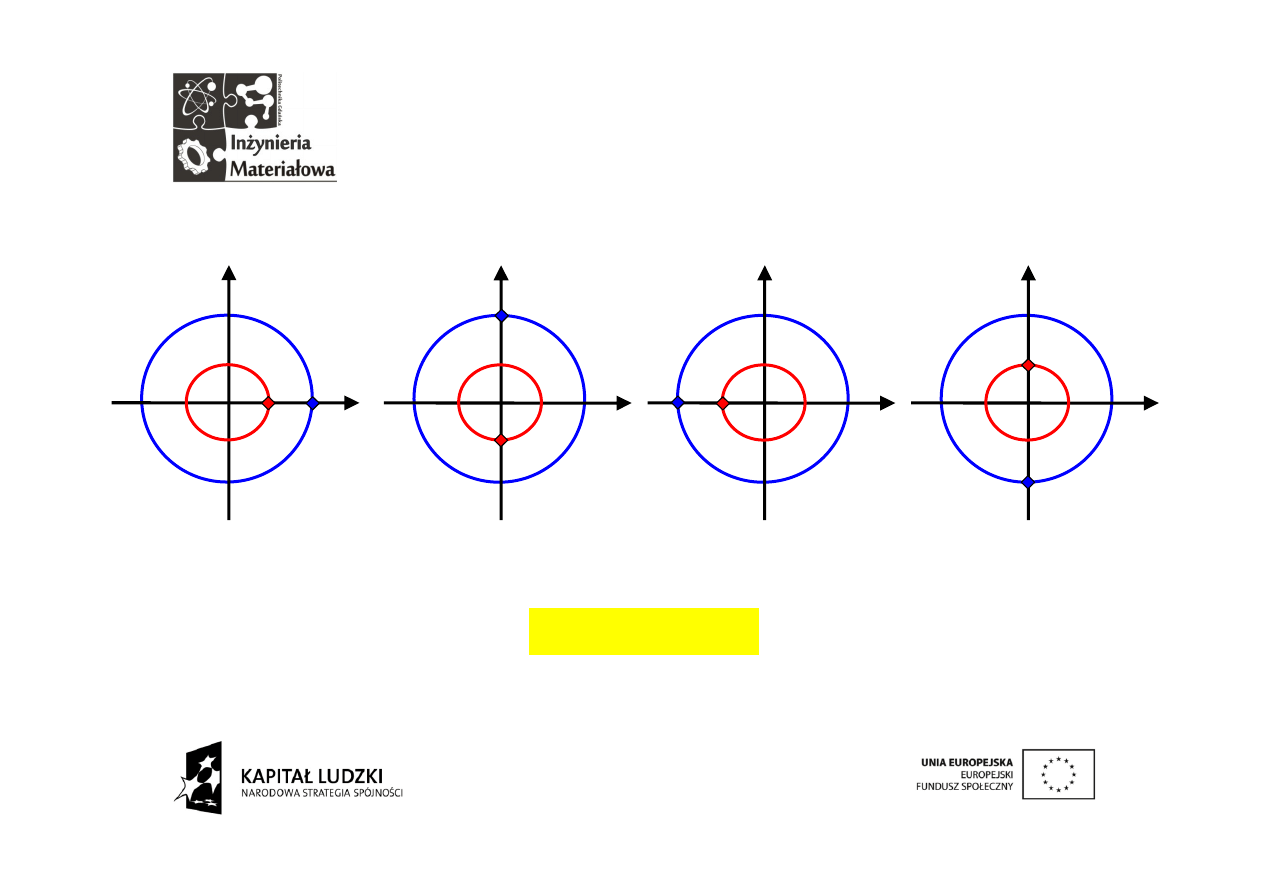
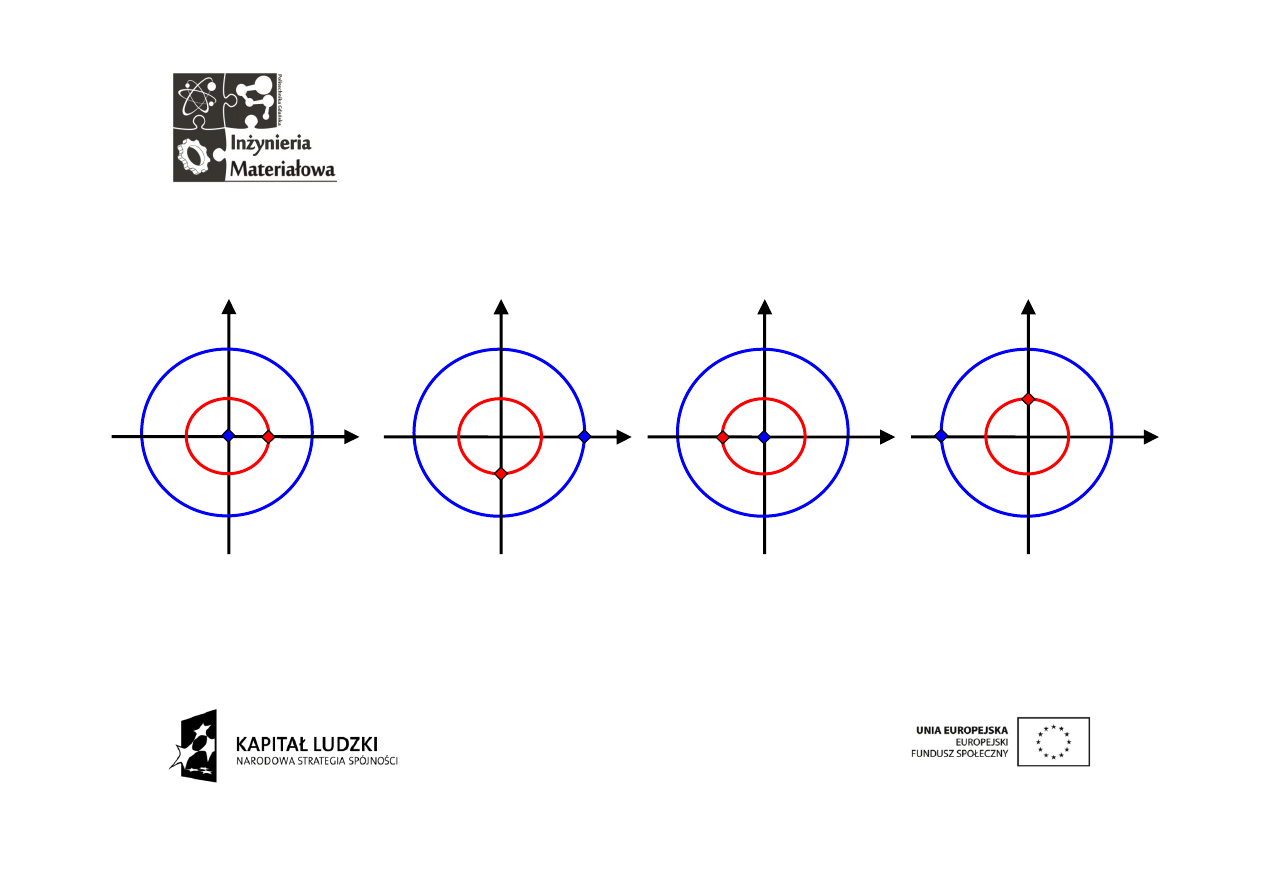
Drugi wektor

Drugi z wektorów obraca się tak samo szybko jak sygnał:

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

iloczyn = A

iloczyn = Aii=-A

iloczyn = -A(-1)=A iloczyn = -Ai(-i)=-A

Dwa podobne wektory dały zero. Wprowadźmy pewną modyfikację
polegającą na zastąpieniu czerwonego wektora analizującego wektorem
sprzężonym. Poprzedniego rysunku nie musimy modyfikować gdyż
pierwszy wektor analizujący był wskazywał zawsze liczbę rzeczywistą.

suma = 0

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

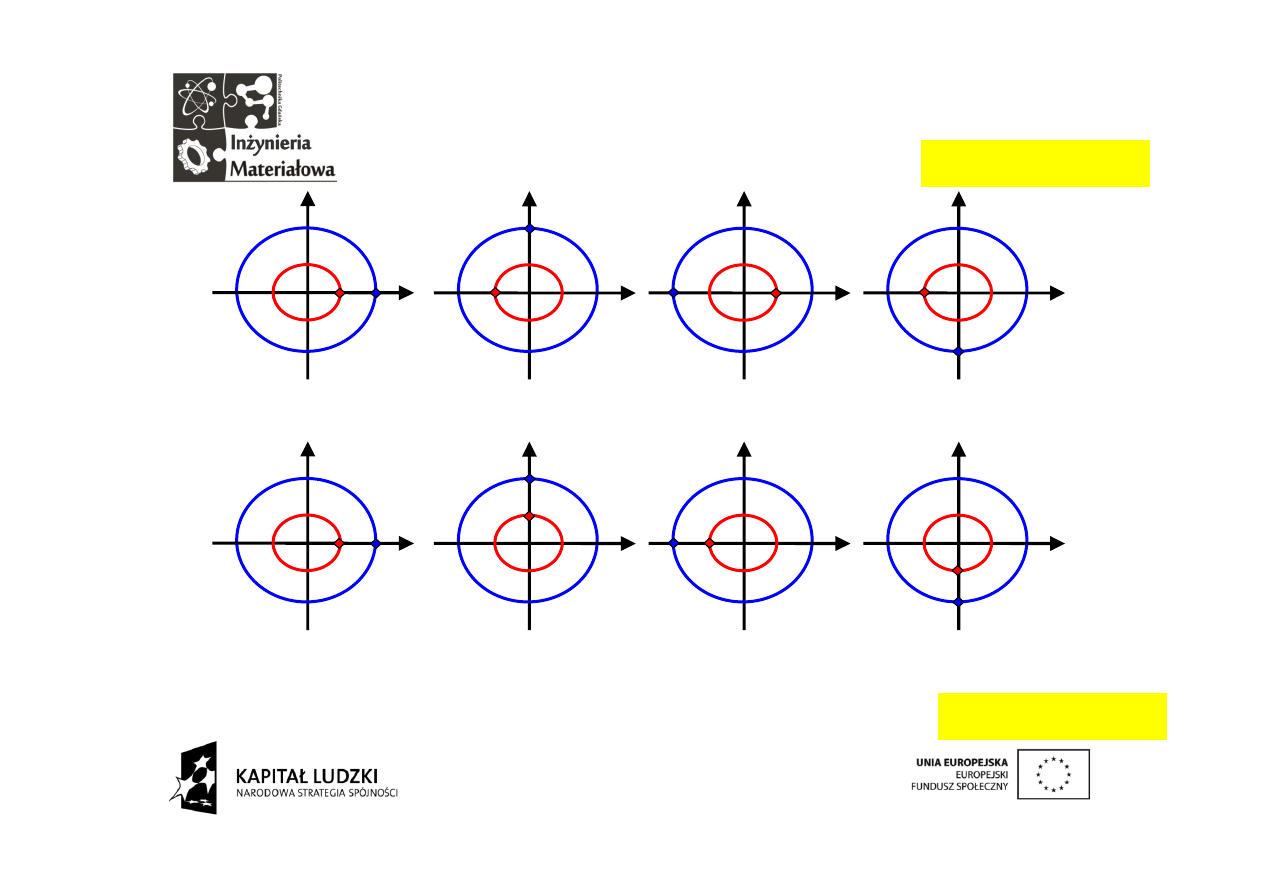
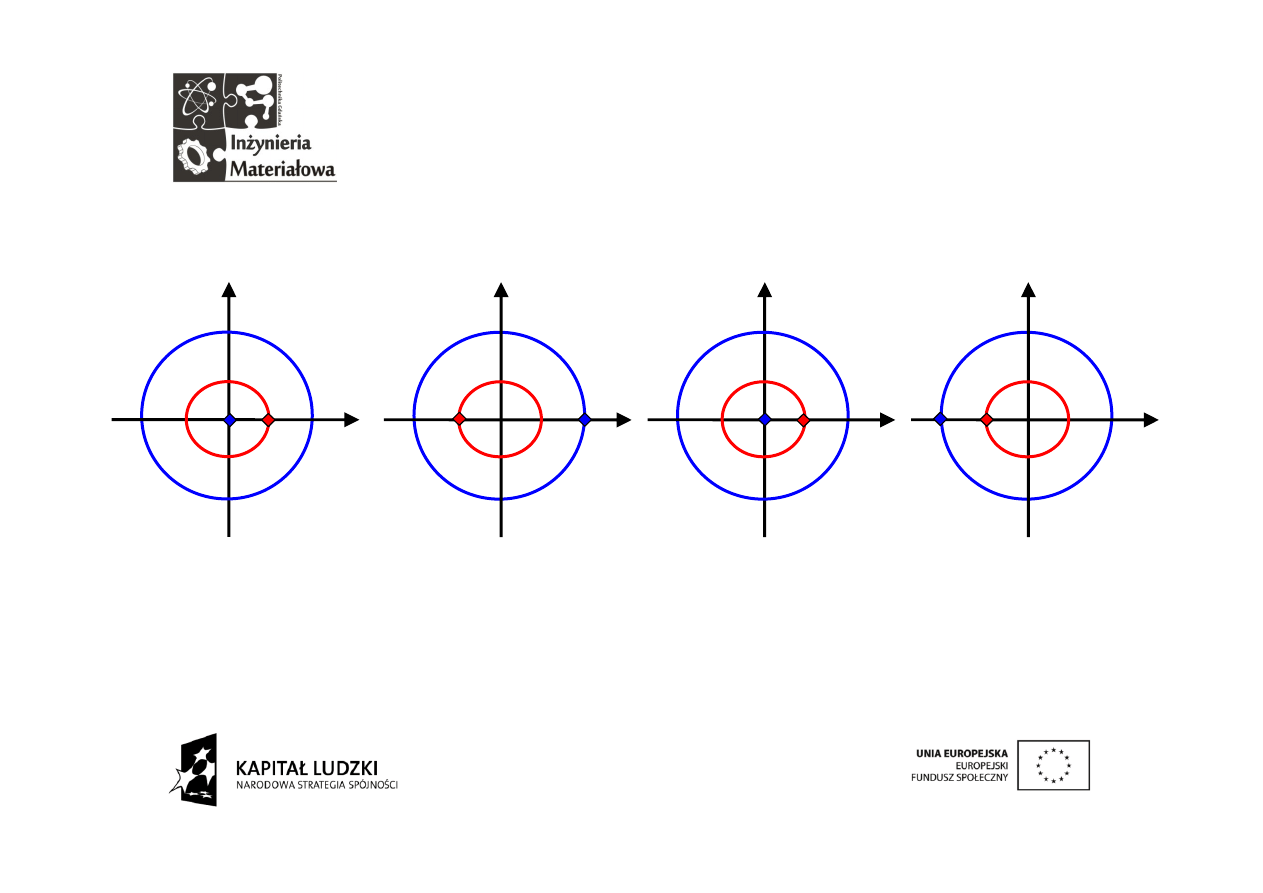
Drugi wektor po raz drugi

Zmodyfikowana sytuacja wygląda tak:

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai(-i)=A

-A(-1)=A

-Aii=A

W wyniku sumowania otrzymujemy wartość niezerową.

suma = 4A

suma = 0

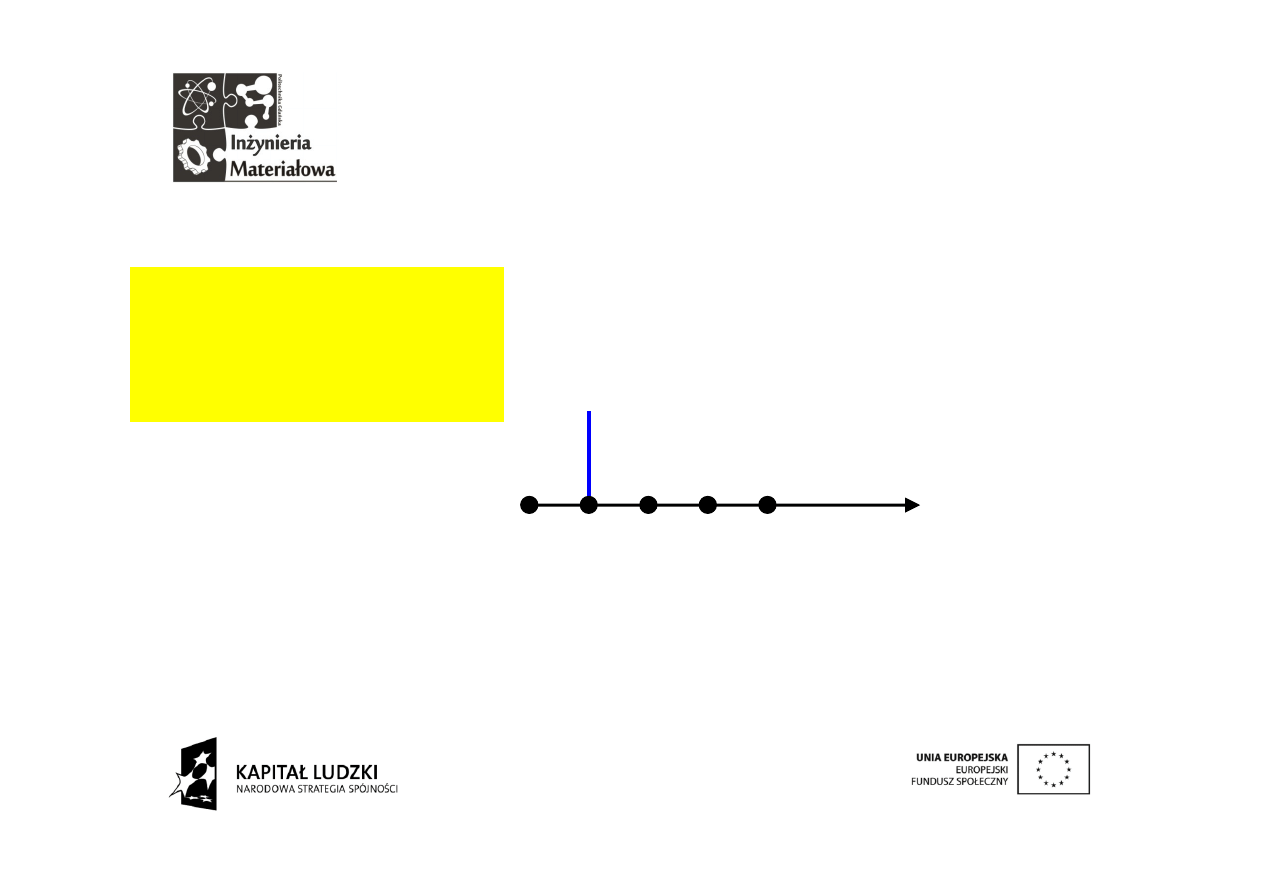
Trzeci i czwarty

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

-Ai

-A

(-1)-Ai=Ai

suma = 0

Dla dwóch ostatnich wektorów znowu otrzymujemy zero.

A

Aii=-A

A

-Ai(-i)=-A

Podsumowanie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Uzyskane rezultaty przedstawiają się następująco:

wektor 0

suma 0

wektor ¼ f

p

suma 4A

wektor 2/4 f

p

suma 0

wektor ¾ f

p

suma 0

Można to narysować otrzymując
widmo częstotliwościowe badanego
sygnału:

f

p

/4

częstotliwość

3/4f

p

Otrzymaliśmy wynik zgodny z intuicją, ponieważ jeden z wektorów o
szybkości zgodnej z szybkością sygnału dał niezerową odpowiedź.
Rzeczywista wartość prążka widmowego wskazuje na fakt, że faza
początkowa sygnału wynosi zero czyli startuje on z osi rzeczywistej.

Trudniejszy przykład

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Poprzedni przykład pokazał nam algorytm ekstrakcji informacji z obiegu
zespolonego. Teraz przyjrzymy się jak będzie wyglądało to w przypadku
funkcji o wartościach rzeczywistych. Będzie to funkcja sinus, która jak
wiemy jest złożeniem dwóch wektorów wirujących w przestrzeni
zespolonej. Najpierw rysunek kolejnych zdjęć powstających w wyniku
próbkowania sinusa.

( )

j

j

ϕ

exp

(

)

j

j

ϕ

−

− exp

czas

Znów wektory

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Ponownie wykonamy korelację, tym razem sygnału sinusoidalnego
z tym samym zbiorem wektorów analizujących:

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

0

A

0

-A

Częstotliwość

sinusoidy

również

wynosi

¼

częstotliwości

próbkowania.

Dla

pierwszego

(nieruchomego)

wektora

otrzymujemy zerową sumę iloczynów.

Wektor synchroniczny

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Teraz znowu wektor o częstotliwości równej częstotliwości funkcji
próbkowanej…

0

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

-iA

0

-iA

Suma podobnie jak w poprzednim przypadku jest niezerowa, ale w
przeciwieństwie do niego jest urojona.

Trzeci wektor

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Iloczyny znoszą się wskazując, że wektory analizujące nie obracają
się w zgodzie z wektorem sygnału analizowanego.

Korelacja z wektorem poruszającym się co

π/2

nie wnosi nic

zaskakującego do naszego obrazu:

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

0

-A

0

A

Czwarty wektor…

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Tutaj spotyka nas niespodzianka. Trzeci wektor o innej szybkości w
wyniku korelacji dał wartość niezerową. Wydaje się to być ciosem w
zaprezentowaną metodykę, jednakże…

Podobnie jak poprzednio na końcu wykonujemy korelację z
czwartym wektorem…

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

A

Ai

-A

-Ai

0

iA

0

-i(-A)=iA

…i jego drugie oblicze

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

wektor przeskakuje o 3/2 π:

0

3/2

π

0

-1/2

π

ale w takich samych miejscach znajdzie się skacząc o minus

π/2

.

DFT…

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Procedura prześledzona przez nas na obrazkach wektorów w przestrzeni
zespolonej jest to dyskretne przekształcenie Fouriera. Ostatni wynik jest
potwierdzeniem postawionej dużo wcześniej tezy mówiącej, że przekształcenie
sygnału prowadzące do jego reprezentacji częstotliwościowej widzi wektory
wirujące w przestrzeni zespolonej a nie rzeczywisty sygnał w dziedzinie czasu.
Przekształcenie zsynchronizowało się (dało niezerowy wynik) w dwóch
przypadkach.

f

p

/4

częstotliwość

f

p

3/4f

p

Jeden z prążków to wirowanie składowej z częstotliwością dodatnią. Drugi to wirowanie
składowej sprzężonej z taką samą co od wartości częstotliwością ujemną.

0

f

p

/4

f

p

3/4f

p

0

-f

p

/4

…widzi funkcje zespolone

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Kolejny dowód to wartości otrzymanych prążków widmowych.

f

p

/4

f

p

3/4f

p

0

-f

p

/4

częstotliwość

-2Ai

2Ai

2Ai

Są to wartości urojone, z których
można wyznaczyć ich kąt fazowy:

0

Kąt fazowy

i

wynosi

90º

0

Kąt fazowy -

i

wynosi

-90º

Wektory startują od kąta zero. Jednak
aby sinus był rzeczywisty oba zostały
podzielone

przez

i.

Podzielenie/pomnożenie

przez

jednostkę urojoną to właśnie obrót o 90

º.

Zatem faza początkowa sinusa

wynosi zero ale wektorów zespolonych
nie.

Podsumowanie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Zespolona

reprezentacja

sygnału

dyskretnego

umożliwiła

pokazanie jak działa algorytm dyskretnego przekształcenia
Fouriera.
DFT wytwarza widmo sygnału informujące o amplitudach i fazach
początkowych jego składowych zespolonych.
Widmo sygnału dyskretnego jest również dyskretne.

Następne zagadnienie

Publikacja współfinansowana

ze środków Unii Europejskiej

w ramach Europejskiego Funduszu Społecznego

Dyskretne przekształcenie Fouriera to potężne narzędzie w analizie
cyfrowej i nie jest ono oczywiście wykonywane w sposób graficzny.
Z tego względu wypada zapisać

matematycznie algorytm

zrealizowany językiem obrazkowym. Jak się okaże zależność
będzie miała wiele wspólnego z wyrażeniem obowiązującym dla
poznanych uprzednio ciągłych sygnałów periodycznych. Należy
jeszcze sprawdzić jak zareaguje DFT na jawne pogwałcenie
twierdzenia o próbkowaniu.