
Całkowa arena
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Zależności opisujące współczynniki szeregu trygonometrycznego
pozostawione zostały bez wytłumaczenia co zostanie nadrobione w
obecnej prezentacji. Podejście stosowane przy wyznaczaniu
współczynników szeregu Fouriera wykorzystywane jest w
algorytmie łączącym czasową i częstotliwościową reprezentację
sygnałów cyfrowych.
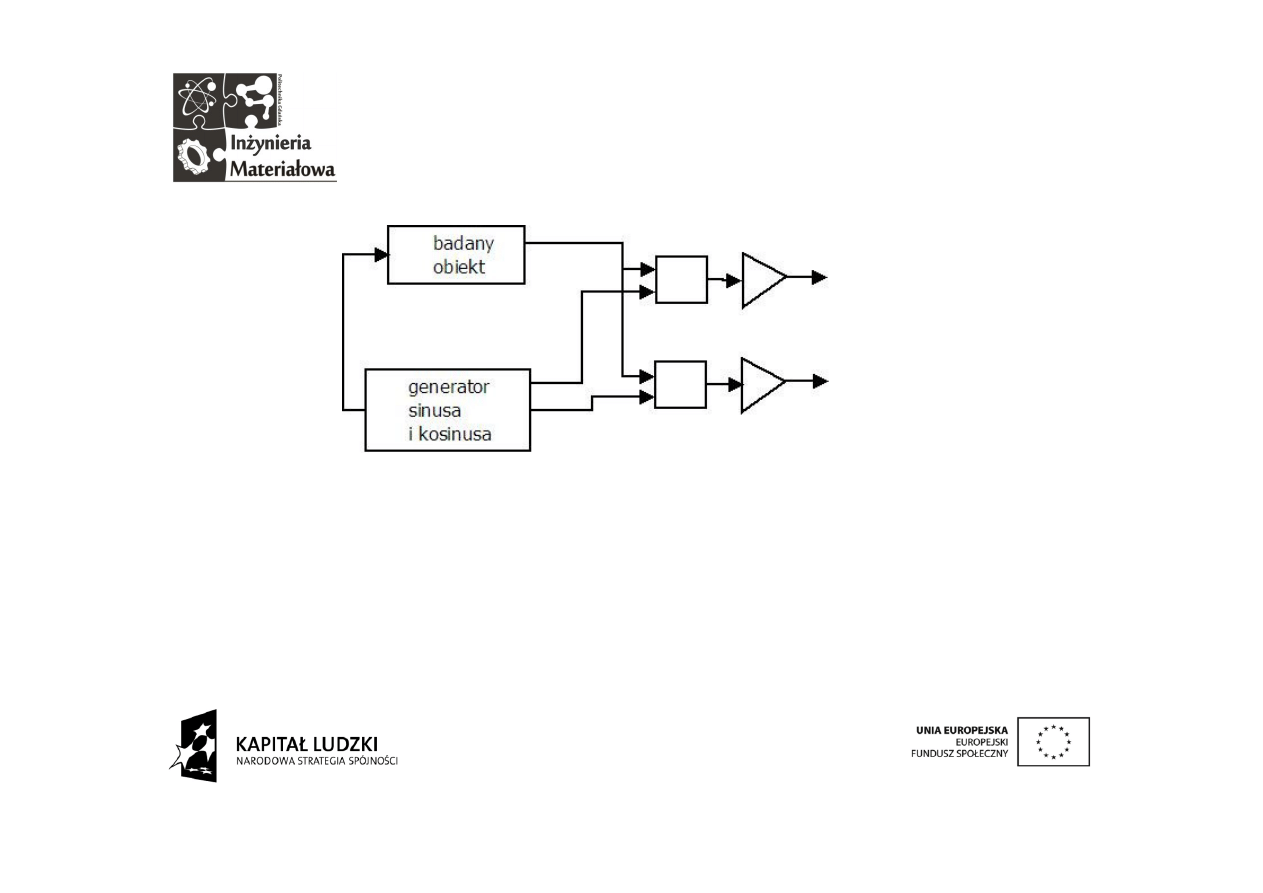
Analizator odpowiedzi
częstotliwościowej
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
FRA to cenne urządzenie w analizie częstotliwościowej układów elektrycznych. Z
powodzeniem jest również stosowany w elektrochemii (w analizie impedancyjnej)
ponieważ zachowanie składników układu elektrochemicznego modelowane jest za
pomocą elektrycznych układów zastępczych. FRA jest systemem analogowym.
( )
t
ω
sin
(
)
ϕ
ω
+
t
sin
( )
t
ω
sin
( )
t
ω
cos
×
×
∫
∫
współczynnik
sinusowy
współczynnik
kosinusowy
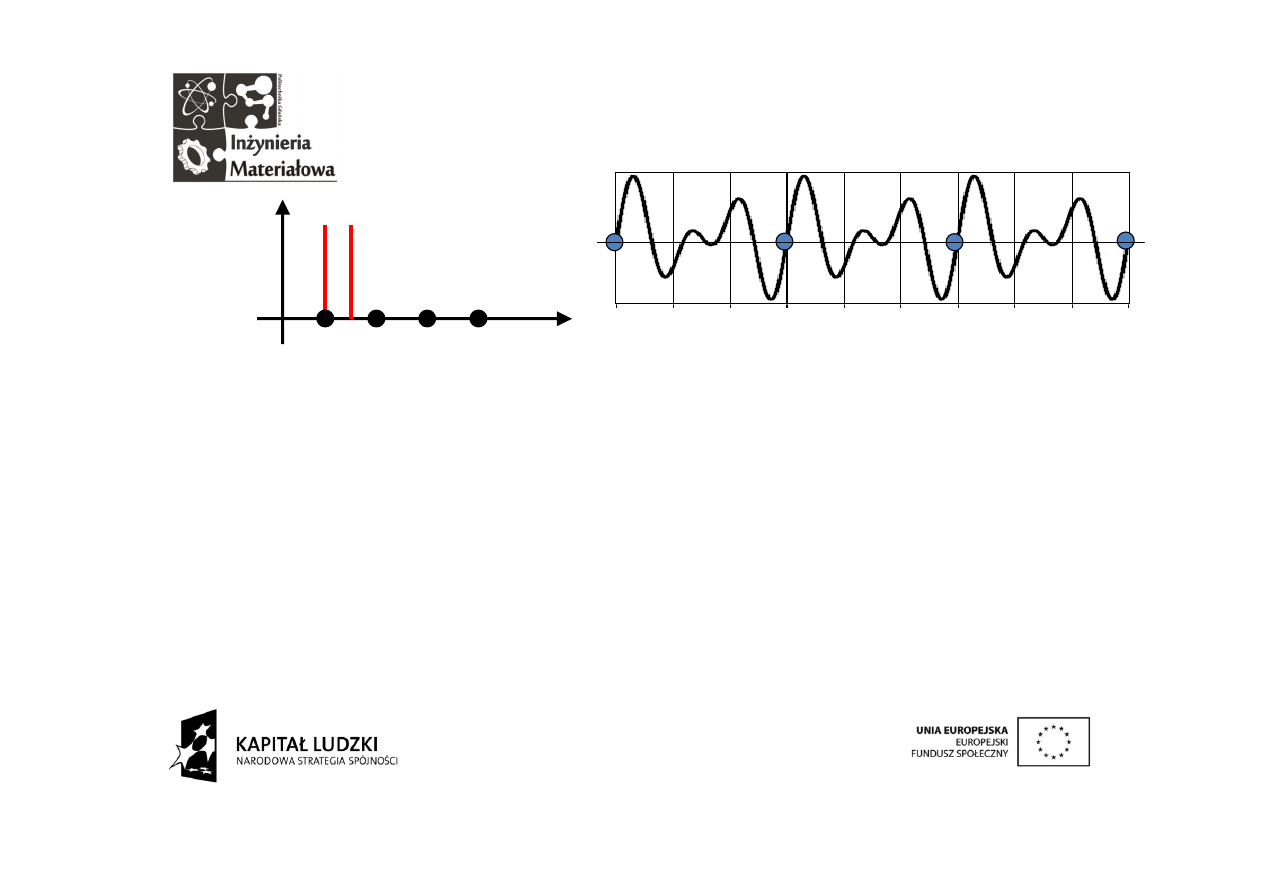
Okresy raz jeszcze
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Dzięki
założeniu
o
wymierności
wzajemnych
stosunków
częstotliwości jesteśmy w stanie określić wspólną wielokrotność
wyznaczającą okres podstawowy. W przedstawionym przykładzie
częstotliwości mają się do siebie jak 3 do 2. Okres podstawowy
wynosi 3 przebieg szybszy mieści się w nim 2 razy, wolniejszy 3.
Częstotliwość podstawowa wynosi 0,5 Hz, f to 2 składowa, a 1,5 f
trzecia.
częstotliwość
f
f
5
,
1

Znowu szereg
trygonometryczny
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Teraz skorzystamy ze wzoru Eulera:
(
)
∑
∞
=
+
+
=
1
0
0
sin
)
(
n
n
n
t
n
A
A
t
s
ϕ
ω
(
)
(
)
∑
∞
=
−
−
−
+
+
=
1
0
0
0
2
exp
exp
)
(
n
n
n
n
i
i
t
in
i
t
in
A
A
t
s
ϕ
ω
ϕ
ω
Własności funkcji wykładniczej pozwalają nam zapisać to w
postaci:
(
)
(
)
(
)
(
)
∑
∞
=
−
−
−
+
=
1
0
0
0
2
exp
exp
exp
exp
)
(
n
n
n
n
i
i
t
in
i
t
in
A
A
t
s
ϕ
ω
ϕ
ω
Nadchodzą wzory
potwory…
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Rozbijamy sumę:
(
)
(
)
(
)
(
)
∑
∑
∞
=
∞
=
−
−
−
+
=
1
0
1
0
0
2
exp
exp
2
exp
exp
)
(
n
n
n
n
n
n
i
i
t
in
A
i
i
t
in
A
A
t
s
ϕ
ω
ϕ
ω
a
to
co
nie
zawiera
wielokrotności
częstotliwości
podstawowej wrzucamy do stałej. Minus wędruje pod drugi
znak sumy
(
)
(
)
(
)
(
)
∑
∑
∞
=
∞
=
−
−
−
+
+
=
1
0
1
0
0
exp
2
exp
exp
2
exp
)
(
n
n
n
n
n
n
t
in
i
i
A
t
in
i
i
A
A
t
s
ω
ϕ
ω
ϕ
ujednolicamy nasz zapis przez wprowadzenie ujemnych n

…niedługo wyjdą za
slajd…
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
stałe oznaczamy jednym symbolem
(
)
(
)
(
)
(
)
∑
∑
∞
−
−
=
∞
=
−
−
+
+
=
1
0
1
0
0
exp
2
exp
exp
2
exp
)
(
n
n
n
n
n
n
t
in
i
i
A
t
in
i
i
A
A
t
s
ω
ϕ
ω
ϕ
(
)
(
)
∑
∑
−∞
−
=
−
∞
=
+
+
=
1
0
1
0
0
exp
exp
)
(
n
n
n
n
t
in
c
t
in
c
A
t
s
ω
ω
Dotychczasowe przekształcenia doprowadziły nas do zapisania
sygnału w dziwacznej formie podczas gdy naszym celem jest
określenie nieznanych współczynników wyrazów sinusoidalnych
(amplitud i faz) oraz wyrazu stałego. Teraz te wielkości pochowały
się w stałych zespolonych ale cały czas mamy wzory pozwalające
je odtworzyć.

Atak całki…
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Teraz uderzamy we wzór całką po jednym okresie podstawowym:
∫
T
dt
t
s
0
)
(
i rozpada się on na trzy części. Rozpracowujemy je po kolei
zaczynając od stałej A
0
:
∫
=
T
T
A
dt
A
0
0
0
to po prostu pole prostokąta o podstawie równej okresowi i
wysokości równej A
0
.
Następne wyrażenie jest gorsze:
(
)
∫∑
∞
=
=
T
n
n
dt
t
in
c
t
s
0
1
0
exp
)
(
ω
…której nie liczymy
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Szereg chcemy scałkować wyraz po wyrazie. Najpierw n=1:
(
)
(
)
(
)
[
]
dt
t
t
i
c
dt
t
i
c
T
T
∫
∫
+
=
0
0
0
1
0
0
1
cos
sin
exp
ω
ω
ω
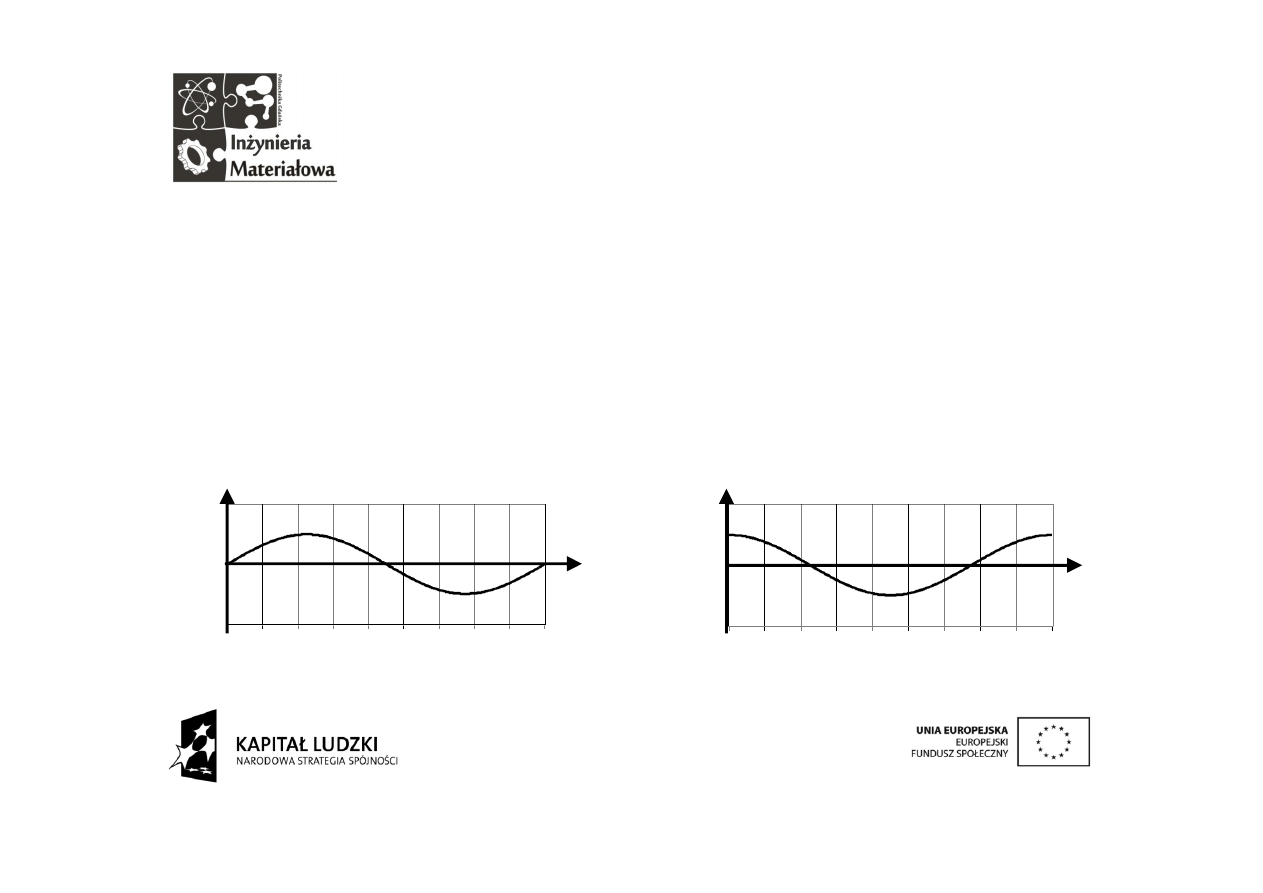
Fala sinusoidalna o częstotliwości
ω
0
mieści
się
w
okresie
podstawowym dokładnie jeden
raz w taki sposób:
0
T
Kosinusoidalna układa się tak:
0
T
u
ro
jo
n
a
rz
e
c
z
y
w
is
ta
Plusy znoszą się z minusami, nie ma szans, żeby któraś ocalała.
Taki sam los spotyka zresztą wyrażenie z –n .
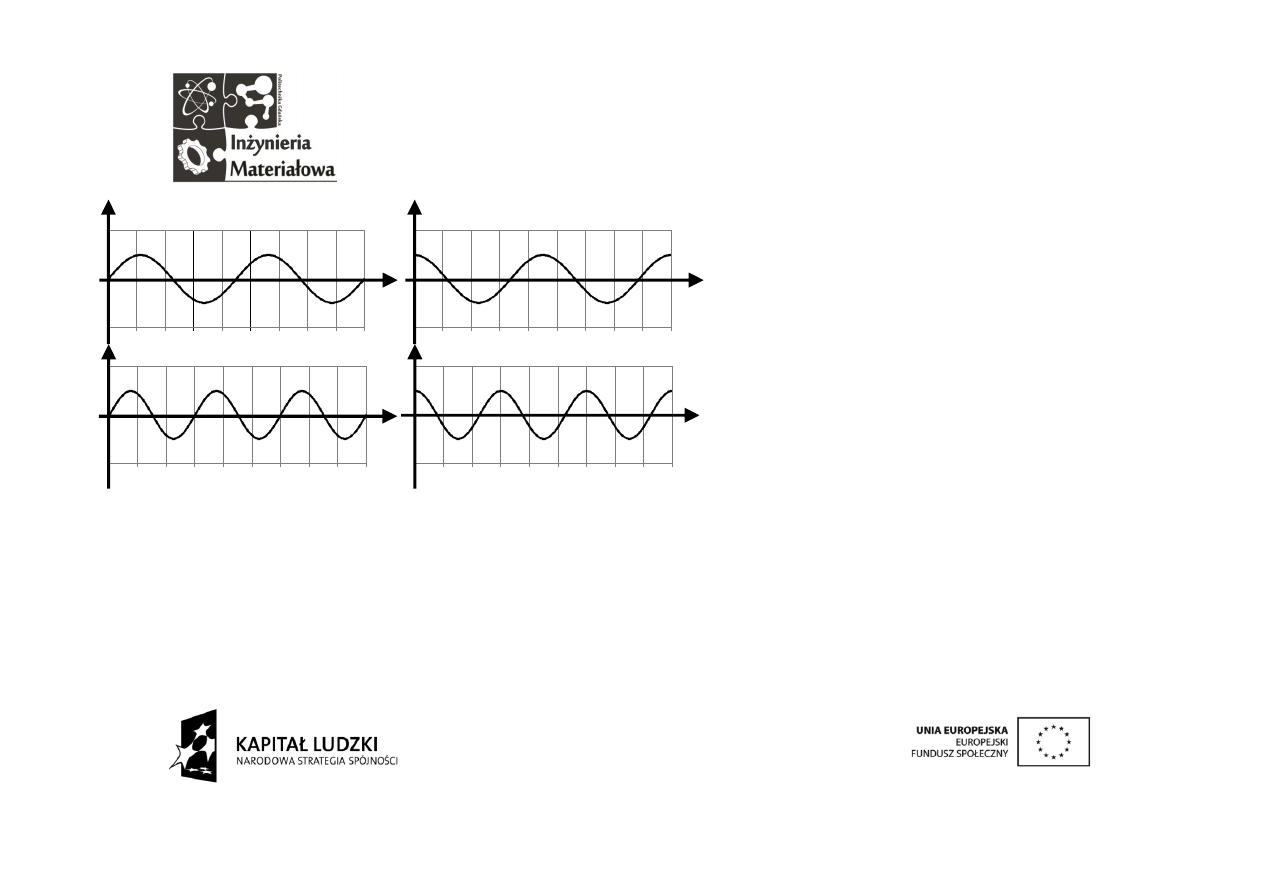
Los składowych harmonicznych
jest przesądzony…
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Ponieważ każda harmoniczna mieści się w okresie podstawowym
całkowitą ilość razy, żadna nie ma szans na przetrwanie. Z
całkowego pogromu wychodzi tylko składowa stała. Dla wygody
można morderczą całkę podzielić przez okres T i wtedy dostarczy
ona od razu wartości poszukiwanej stałej A
0
.
(
)
(
)
[
]
dt
t
t
i
c
T
∫
+
0
0
0
2
2
cos
2
sin
ω
ω
(
)
(
)
[
]
dt
t
t
i
c
T
∫
+
−
0
0
0
2
2
cos
2
sin
ω
ω
(
)
(
)
[
]
dt
t
t
i
c
T
∫
+
0
0
0
3
3
cos
3
sin
ω
ω
(
)
(
)
[
]
dt
t
t
i
c
T
∫
+
−
0
0
0
3
3
cos
3
sin
ω
ω
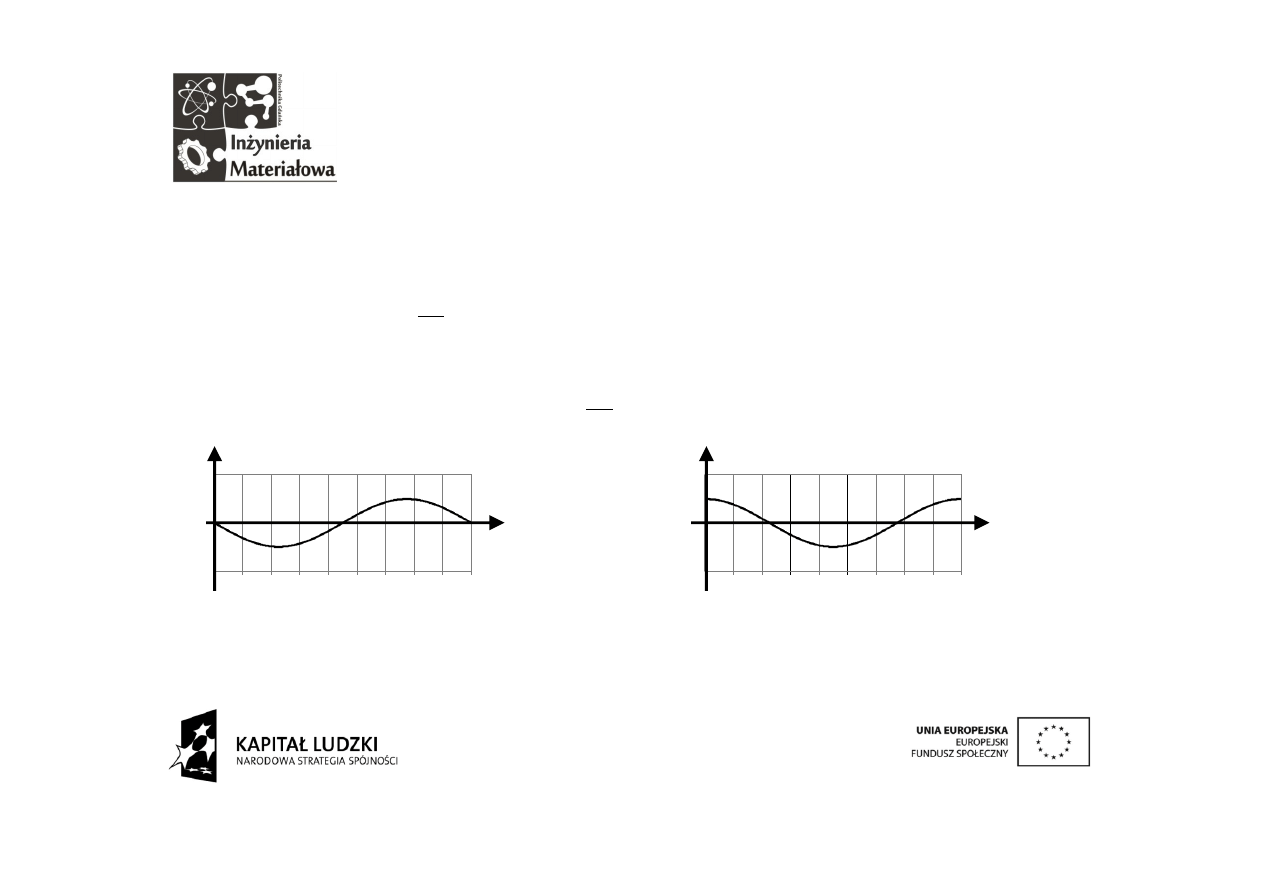
Inwazja całek
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
To oczywiście nie koniec, ponieważ teraz na arenę wkracza całka
uzbrojona w dodatkowe wyrażenie:
(
)
∫
−
T
dt
t
j
t
s
T
0
0
exp
)
(
1
ω
Najpierw składowa stała:
(
)
∫
−
T
dt
t
j
A
T
0
0
0
exp
1
ω
Sinus jest nieparzysty, kosinus parzysty ale to już widzieliśmy.
Całka niszczy samą siebie przy okazji pociągając wyrażenie stałe.

Równi wojownicy
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Po ataku samobójczym przychodzi czas na main event czyli
spotkanie wyrażeń o takich samych częstościach…
(
)
(
)
∫
−
T
dt
t
j
t
j
c
T
0
0
0
1
exp
exp
1
ω
ω
…i szumnie zapowiadane starcie szybko się kończy:
(
)
(
)
1
0
0
0
1
exp
exp
1
c
dt
t
j
t
j
c
T
T
=
∫
ω
ω
Pozostawiając w rezultacie wyznaczoną wartość współczynnika c
1
.
Wprowadzenie czynnika 1/T ułatwia obliczenia.
Wyrażenie symetryczne w
szeregu…
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Opisujące człon z –n w tym przypadku zachowuje się inaczej:
(
)
(
)
∫
−
−
−
T
dt
t
j
t
j
c
T
0
0
0
1
exp
exp
1
ω
ω
(
)
∫
−
−
T
dt
t
j
c
T
0
0
1
2
exp
1
ω
Czyli:
W wyniku całkowania powstaje wyrażenie o dwa razy większej
częstotliwości.
Nietrudno zgadnąć co się
stanie…
…i symetryczna całka
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Skoro była całka z ujemnym argumentem funkcji wykładniczej to
jest też jej „siostra” z dodatnim. Tutaj jednak nie dzieje się nic
nowego:
(
)
(
)
(
)
∫
∫
=
T
T
dt
t
j
T
dt
t
j
t
j
c
T
0
0
0
0
0
1
2
exp
1
exp
exp
1
ω
ω
ω
(
)
(
)
∫
−
−
=
−
T
c
dt
t
j
t
j
c
T
0
1
0
0
1
exp
exp
1
ω
ω
Otrzymaliśmy przepis na współczynnik c
-1

Mniejszy vs większy
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
To starcie nie skończyło się zwycięstwem całek. Wzywają więc
szybszego przeciwnika…
(
)
(
)
(
)
∫
∫
=
T
T
dt
t
j
T
dt
t
j
t
j
c
T
0
0
0
0
0
1
3
exp
1
2
exp
exp
1
ω
ω
ω
Widoczne jest, że spotkania stają się rutynowe i nudne. W ich
wyniku
zawsze
otrzymujemy
przebiegi
trygonometryczne
mieszczące się w okresie całkowitym a więc całkowanie powoduje
zerowanie zarówno dla wyrażeń dodatnich jak i ujemnych.
(
)
(
)
(
)
[
]
∫
∫
+
=
T
T
dt
t
j
n
T
dt
t
nj
t
j
c
T
0
0
0
0
0
1
1
exp
1
exp
exp
1
ω
ω
ω
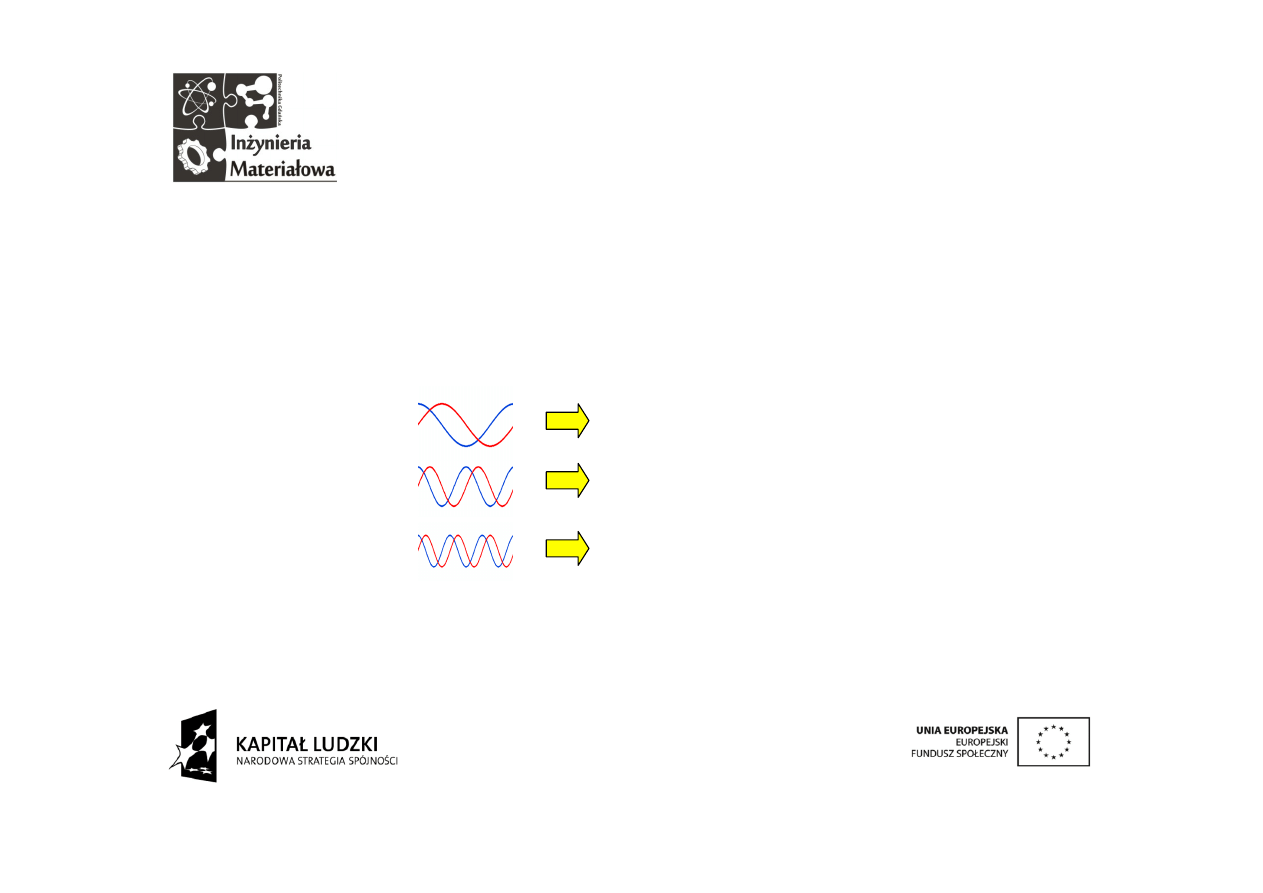
Próba uogólnienia
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Łatwo
wydedukować
czy
nawet
wyliczyć
powtarzając
przedstawiony, nużący tok rozumowania, że zastosowanie rodziny
całek zawierających wyrażenia z rosnącymi częstotliwościami
pozwoli wyodrębnić współczynniki kolejnych wyrazów szeregu.
( )
∫
( )
∫
( )
∫
0
1
ω
0
2
ω
0
3
ω
1
1
,
−
c
c
2
2
,
−
c
c
3
3
,
−
c
c
Otrzymujemy metodę ekstrakcji informacji o każdej składowej
szeregu Fouriera.

Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Możemy pozbyć się innej postaci całki dla wyrazu stałego
przyjmując, że:
Próba uogólnienia II
( )
(
)
∫
∫
=
T
T
dt
t
j
t
s
T
dt
t
s
T
0
0
0
0
exp
1
)
(
1
ω
wówczas wrażenie na kolejne współczynniki c
n
przyjmie postać:
( )
(
)
dt
t
jn
t
s
T
c
T
n
∫
−
=
0
0
exp
1
ω
c
n
można podzielić na część rzeczywistą i urojoną:
( )
(
)
(
)
∫
∫
−
=
+
=
T
T
n
n
n
dt
t
n
t
is
T
dt
t
n
t
s
T
ib
a
c
0
0
0
0
sin
)
(
1
cos
1
ω
ω
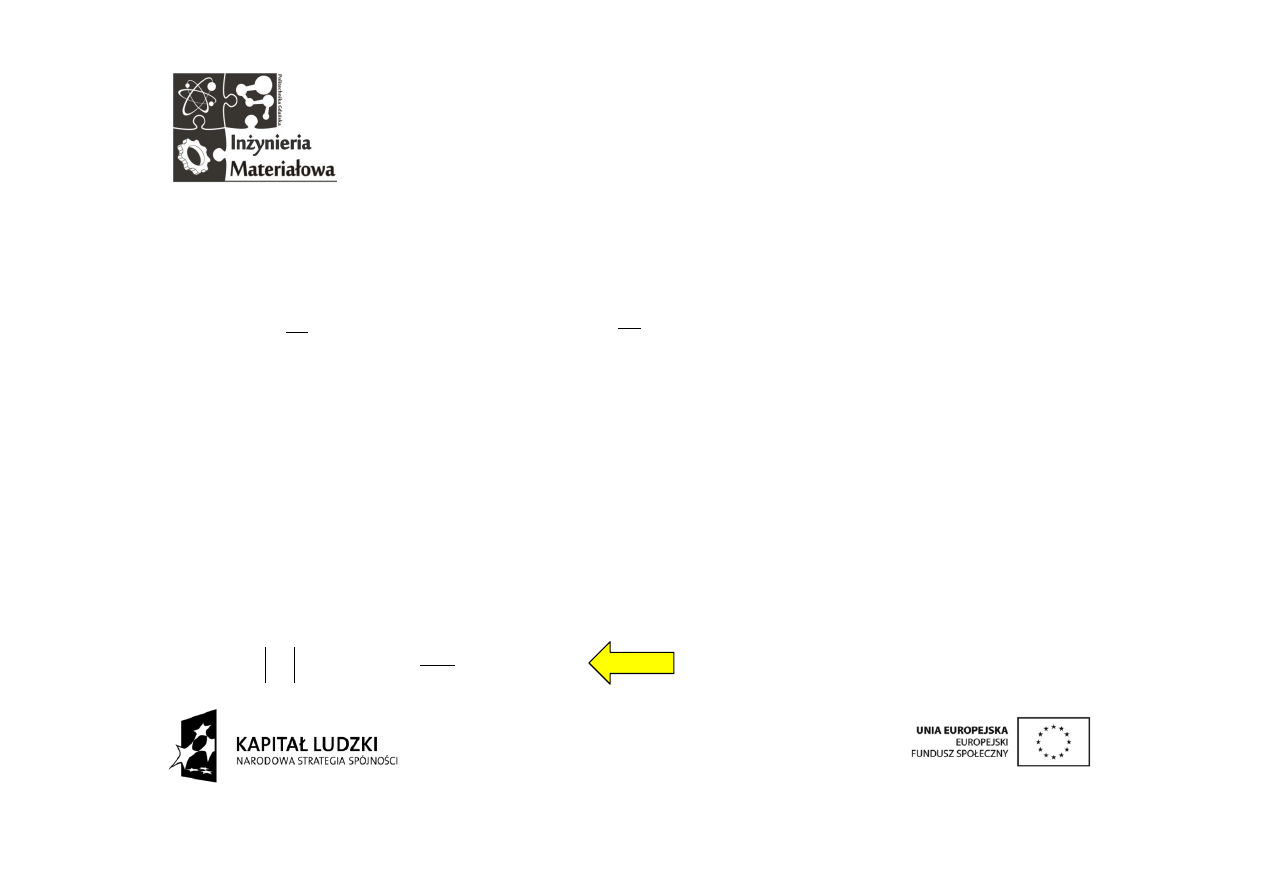
Tajemniczy wzór z
poprzedniego wykładu
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Po separacji części rzeczywistej i urojonej otrzymujemy:
( )
(
)
dt
t
n
t
s
T
a
T
n
∫
=
0
0
cos
1
ω
( )
(
)
dt
t
n
t
s
T
b
T
n
∫
=
0
0
sin
1
ω
Musimy jeszcze uwzględnić, że para sinus i kosinus to para
prążków c
n
i c
-n
. Skoro rozpisany został tylko jeden to jest o połowę
za mały. Pomnożenie całek przez 2 kompensuje ten efekt. W taki
sposób wyjaśniają się podane uprzednio wzory na współczynniki
szeregu Fouriera. Wyrażenia na c możemy również rozpisać na
składową amplitudową (moduł) i fazową:
( )
( )
ϕ
ϕ
i
A
i
c
c
n
n
n
exp
2
exp
=
=
Współczynnik reprezentacji
wykładniczej jest 2 razy
mniejszy niż sinusoidalnej.
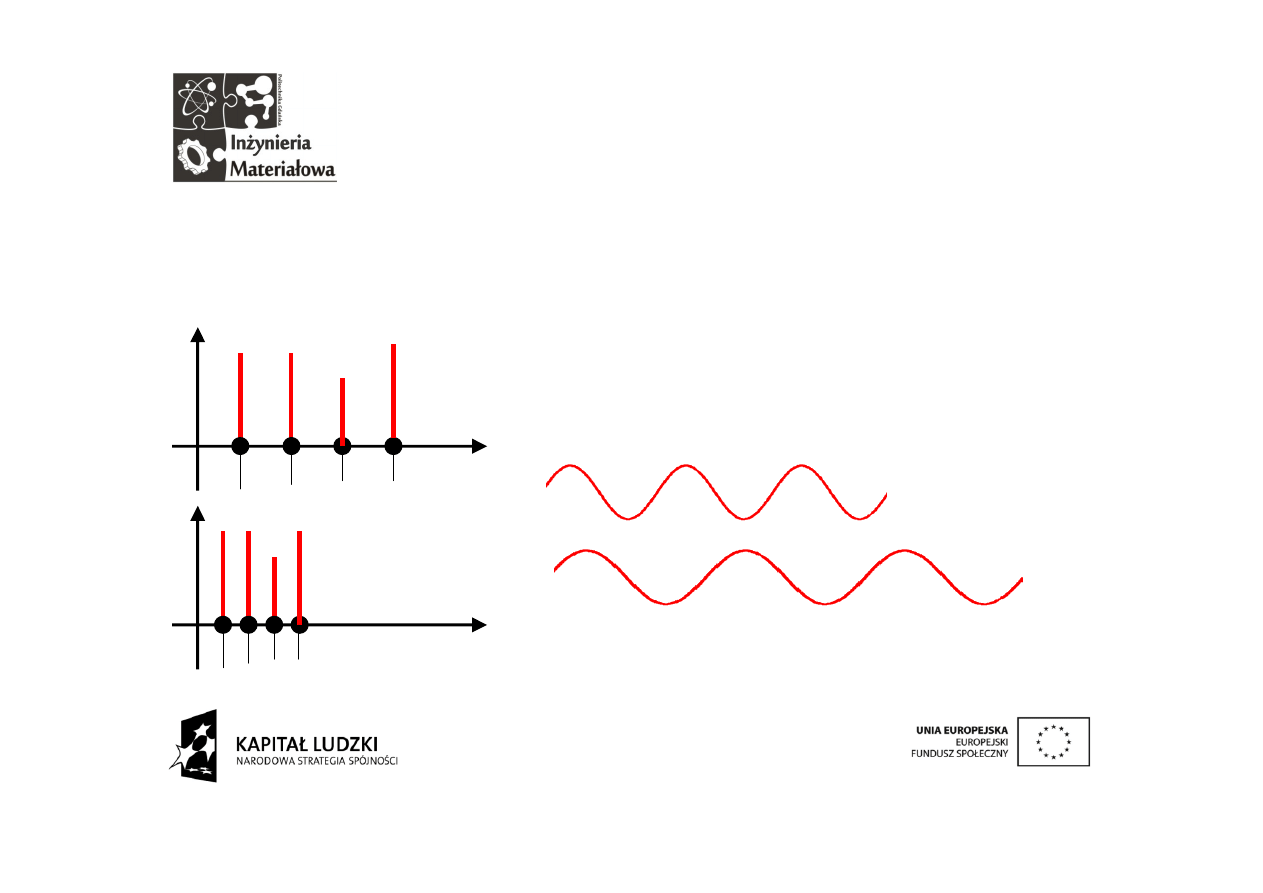
Niedyskretny szereg
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Szereg Fouriera jest dyskretny w dziedzinie częstotliwości. Składa
się z prążków, które utożsamiamy ze współczynnikami rozwinięcia.
Prążki opisują składową amplitudową i fazową.
Pierwszy prążek to f
0
drugi 2f
0
,
odległość
między kolejnymi prążkami jest stała i
wynosi f
0
.
0
f
0
f
0
f
0
f
zwiększamy
okres…
0
f
0
f
0
f
0
f
…tym samym zmniejszając częstotliwość
podstawową i odległość między prążkami.
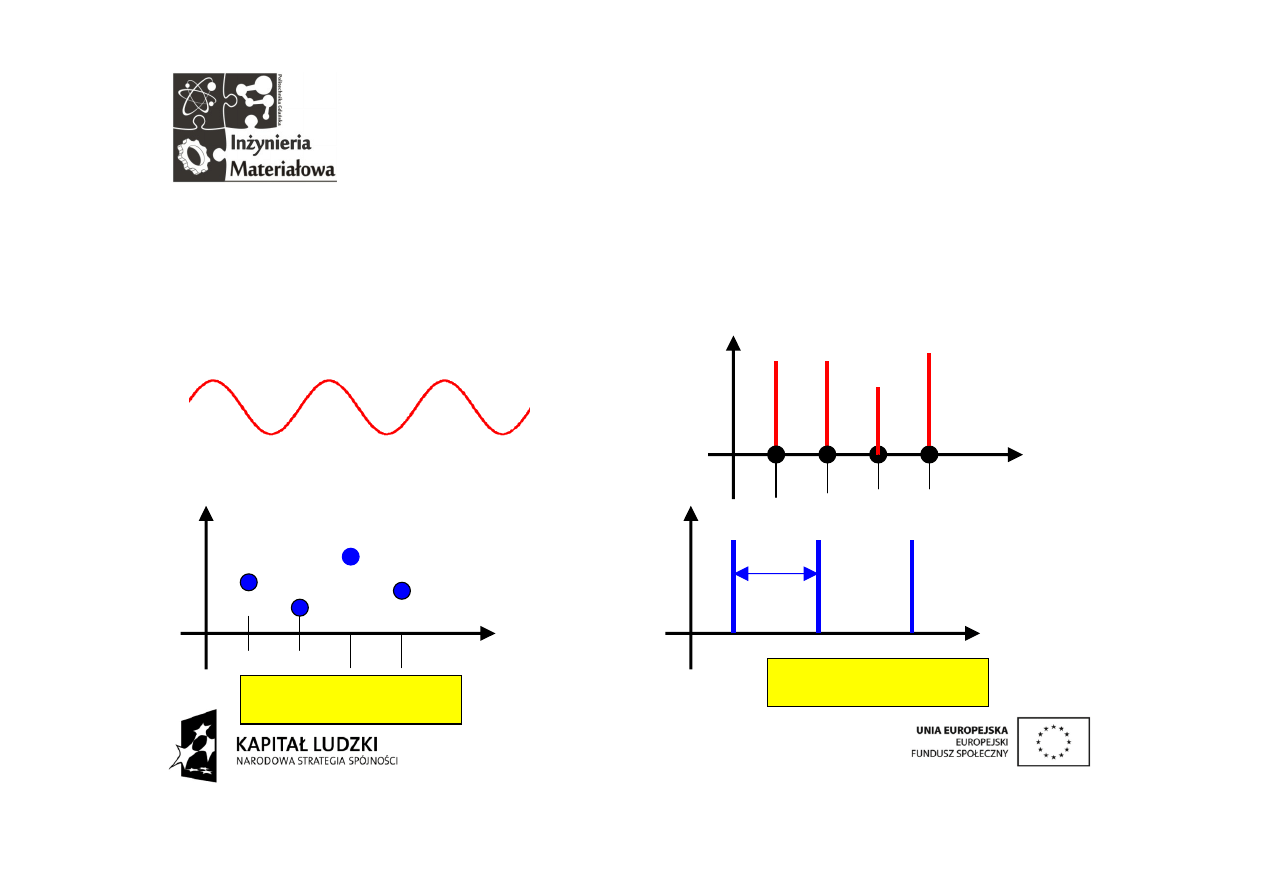
Granica
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Wydłużając okres podstawowy w granicy doprowadzamy do zlania
się
prążków w ciągłą
funkcję
częstotliwości. Funkcja o
nieskończonym okresie to funkcja nieokresowa a szereg ją
opisujący to już nie szereg tylko funkcja.
czas
częstotliwość
okresowy
dyskretny
p
f

Podsumowanie
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Szereg Fouriera opisuje periodyczny przebieg ciągły za pomocą
złożenia funkcji sinus i kosinus, które mogą zostać zamienione na
swoje odpowiedniki wykładnicze.
Operacja mnożenia i całkowania prowadzi do wyselekcjonowania
pojedynczych składowych częstotliwościowych. Operacja tego typu
to iloczyn skalarny.

Kolejne zagadnienie
Publikacja współfinansowana
ze środków Unii Europejskiej
w ramach Europejskiego Funduszu Społecznego
Obecność całek wciąż więzi nas w królestwie przebiegów ciągłych
(analogowych). Jest to sytuacja nieprzystająca do przetwarzania
cyfrowego
dlatego
zależności
powinny
zostać
poddane
dyskretyzacji.
Sens wyrażeń na współczynniki rozwinięcia łatwiej jest zobaczyć
przy wykorzystaniu obrazków z obrotami w przestrzeni zespolonej.
Jak się okaże selektywność wyrażenia całkowego „filtrującego”
składowe o określonych częstotliwościach obowiązywać będzie
także w przypadku dyskretnym choć same całki znikną.
Wyszukiwarka
Podobne podstrony:
miernictwo1 wyklad4
miernictwo wyklad 09, INNE MATERIAŁY
miernictwo wyklad 05, INNE MATERIAŁY
miernictwo1 wyklad 3 id 776866 Nieznany
miernictwo1 wyklad3
miernictwo1 wyklad7
miernictwo wyklad 01, INNE MATERIAŁY
miernictwo1 wyklad10
miernictwo wyklad 11, INNE MATERIAŁY
Geodezja i miernictwo wyklad 1, GEODEZJA(1)(1)
miernictwo wyklad 04, INNE MATERIAŁY
miernictwo wyklad 10, INNE MATERIAŁY
miernictwo wyklad 03, INNE MATERIAŁY
miernictwo wyklad 06, INNE MATERIAŁY
miernictwo1 wyklad9
miernictwo1 wyklad5
miernictwo1 wyklad3
miernictwo wyklad 08, INNE MATERIAŁY
więcej podobnych podstron