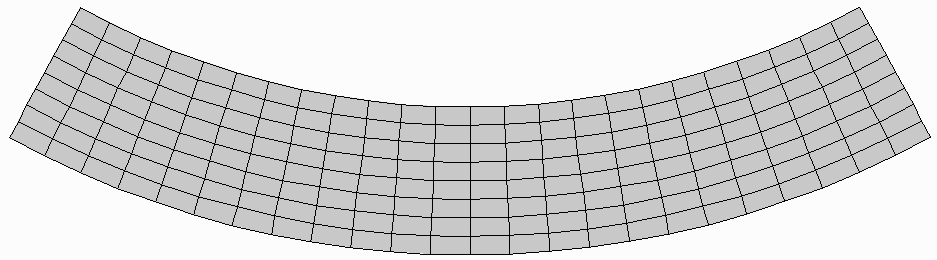
Naprężenia i odkształcenia w pręcie równomiernie zginanym Czyste zginanie – bez działania siły poprzecznej.

W każdy przekroju pręt obciążony momentem gnącym o stałej wartości.

Linie prostopadłe do osi pręta, np. bb i cc, pozostają proste, a kontur nadal płaski. Całe przekroje zachowują swoją płaskość. Dzieląc w myśli belkę na podłużne elementy, zwane włóknami – po stronie wklęsłej ulegają skróceniu i odległości między przekrojami prostopadłymi do osi zmniejszyły się.

W pręcie istnieje warstwa, w której włókna nie zmieniły swojej długości.

Warstwa – warstwa obojętna, a ślad w płaszczyźnie przekroju pręta – linią ( osią) oboję tną. W przekroju występują napręż enia normalne.

b

c

M

M

g

g

x z

M

b

c

x

y

dx

y

x

y

dx

Mg

Mg

x

b’

c’

b’

c’

a)

b

c

M

M

g

g

x z

M

b

c

x

y

dx

y

x

y

dx

b)

dϕ

ρ

y

dA

-

M

σ

g

σ

z

ds=dx

y

y

ds(1+ε)

y +

ds(1 + ε) = ds

− ρ +

y

− ρ

M

ρ

g

Mg

x

y

Po odkształceniu wszystkie linie siatki są do siebie prostopadłe 1. Warunki geometryczne

Rys. a) – pręt przed odkształceniem i po zgięciu (rys. b).

y – włókno odległe od osi obojętnej – długość pierwotna dx = ds , po odkształceniu wynosi ds 1

( + ε ) , ε − wydłużenie właściwe. Z zależności geometrycznych ds(1 + ε) = ds

− ρ +

a stąd

y

− ρ

ε = − y (1) ρ

ρ − promień krzywizny warstwy obojętnej.

Siły zewnętrzne działające po jednej stronie przekroju belki redukują się do momentu Mg.

Uwzględniając wewnętrzne siły elementarne σ dA tworząc przestrzenny układ sił

równoległych, można dla odciętej części belki napisać równania równowagi.

2. Warunki równowagi

∑P = ,0

∫ σ dA = 0 (2) x

A

∑M = ,0

∫ z σ dA = 0 (3) y

A

∑M

(4)

z =

,

0

∫ y σ dA − Mg = 0

A

3. Warunki fizyczne (prawo Hooke’a):

σ = E ε.

Wykorzystując warunki geometryczne otrzymujemy: y

σ = −E (5) ρ

Rozkład naprężeń w przekroju – wartość proporcjonalna do odległości od osi obojętnej przekroju.

− E ∫ y dA = ,0

A

ρ

− E ∫ y z dA = ,0 (6) A

ρ

− E ∫ y 2 dA = Mg A

ρ

Uwzględniając ∫ y 2 dA = I osiowy moment bezwładności, można zapisać z

A

1

M g

= −

ρ

, EIz – sztywność na zginanie.

EI z

σ

Wstawiając − 1 =

ρ

Ey

M y

g

σ =

Iz

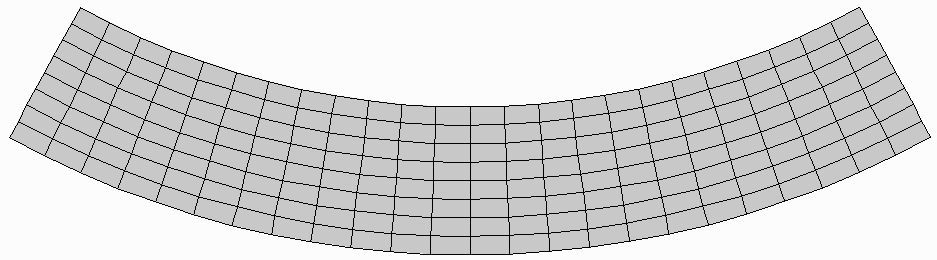
Wytrzymałość na zginanie

Naprężenia w przekrojach poprzecznych belki. Zauważalne różnice promienia krzywizny włókien poprzecznych ρ’.

Wytrzymałość na zginanie.

σ1

e1

Oś obojętna

σ

e2

σ2

y

y

e

σ = M 1 ,

1

g Iz

e

σ = M 2 .

2

g Iz

I

I

M

M

Przyjmuj

g

g

ąc

z

z

W =

,

W =

, otrzymujemy σ =

,

σ =

, gdzie W

1

2

1, W2

e

e

1

2

W

W

1

2

1

2

są to wskaźniki wytrzymałości na zginanie. Jeżeli e1=e2, W1=W2 = W i wtedy warunek wytrzymałości belki zginanej będzie miał postać: M

g = σ

≤ σ .

max

dop

W