ZADANIE 1

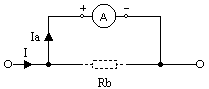
Amperomierz o oporze wewnętrznym Ra = 10Ω i prądzie przy pełnym wychyleniu Ia = 15mA chcemy przystosować do pomiarów prądu I w zakresie 0 ÷ 1,5A. Obliczyć wartość opornika bocznikującego Rd i opór wewnętrzny Ra’ nowego przyrządu.

Rozwiązanie

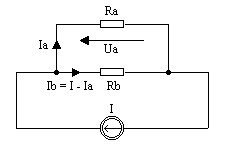
Zastępując amperomierz jego oporem wewnętrznym otrzymamy dla I = 1,5A schemat równoważny obwodowi tematowemu

Z prawa Ohma i I prawa Kirchhoffa

Ua = Ia ⋅ Ra = ( I − Ia)⋅ Rb

stąd

Ia

1

Rb = Ra ⋅

= Ra ⋅

I − Ia

I −1

Ia

Po podstawieniu wartości liczbowych 1

10

Rb = 10

=

Ω ≅ 0,101Ω

100 −1 99

a opór wewnętrzny nowego przyrządu

Ra ⋅ Rb

Ra' =

= 0,1Ω

Ra + Rb

ZADANIE 2

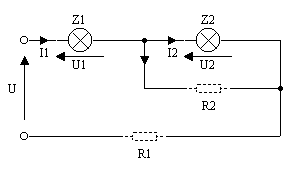
Dwie żarówki chcemy załączyć na napięcie U = 220V. Dobrać wartości oporników dodatkowych R1 i R2 tak, by żarówki te pracowały w warunkach znamionowych.

Parametry znamionowe żarówek:

Z1: U1 = 12V, I1 = 50mA

Z2: U2 = 48V, I2 = 20mA.

Rozwiązanie

Zastępując żarówki Z1 i Z2 ich oporami w punktach pracy otrzymamy Ponieważ

U − U1 − U2 − Ur1 = 0

więc

U − U1 − U2

R1 =

= 3,2kΩ

I1

natomiast

U2 = ( I1 − I2) ⋅ R2

zatem

U2

R2 =

= 1,6kΩ

I1 − I2

ZADANIE 3

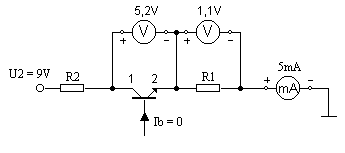
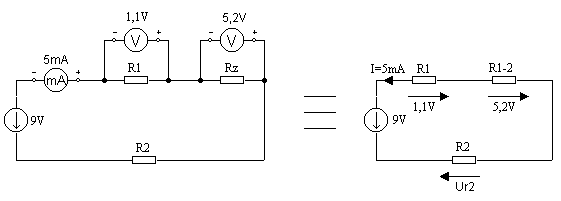
W podanym obwodzie (fragment obwodu tranzystorowego na rysunku) obliczyć, na podstawie wskazań przyrządów, wartości oporników R1, R2 oraz oporność zastępczą Rz między punktami 1 i 2.

Rozwiązanie

Rozpatrywany fragment układu można przedstawić jak na rysunkach poniżej.

Z prawa Ohma:

1,1

R1 =

= 220Ω

5 ⋅ 10−3

Ur2

9 − 1,1 − 5,2

R2 =

=

= 540Ω

I

5 ⋅ 10−3

5,2

Rz =

= 1040Ω

5 ⋅10−3

ZADANIE 4

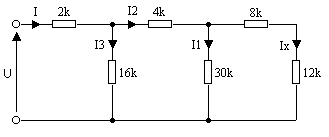
Obliczyć wartość prądu Ix w obwodzie przedstawionym na rysunku, jeśli wiadomo, że prąd I wydawany przez źródło ma wartość 10mA.

Rozwiązanie

Proponujemy, spośród metod które można zastosować do obliczenia prądu Ix, metodę następującą:

1. przyjmujemy dowolną wartośc prądu Ix np. Ix’ = 1mA, 2. obliczamy prądy I1’, I2’, I3’, I’, 3. obliczamy (korzystając z liniowości obwodu) prąd Ix z zależności

I

Ix = Ix' ⋅

= k ⋅ Ix'

I'

Metoda ta nosi nazwę „metody od końca” i jest analogiczna do znanych metod rozwiązywania układów łańcuchowych.

Podstawiając wartości (w obliczeniach stosujemy jenostki mA, kΩ, V) otrzymujemy

Ix' = 1mA

20V

2

I1' =

= mA

30kΩ

3

2

5

I2' = 1 + = mA 3

3

a

5

I3' ⋅16 = ⋅ 4 + 1 ⋅ 20

3

czyli

5

I3' = mA

3

oraz

10

I' = I3' + I2' =

mA

3

więc

I

k =

= 3

I'

stąd wynik

Ix = k ⋅ Ix' = 3mA