STEEL RAILWAY BRIDGE DESIGN
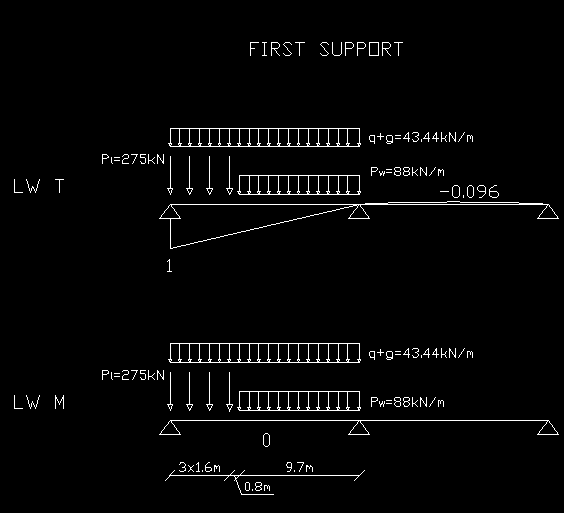
1.2 Influence lines and internal forces kN
q := 1.689
P :=
L := 15.3m
m
l
275kN
kN
kN
P
:=
w
88
g := 41.75
m
m
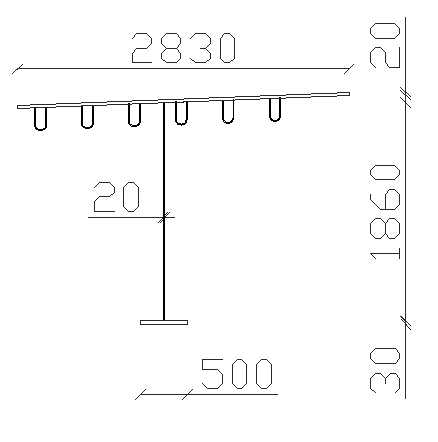
CROSS SECTION A - A 1
9.7 × 0.555
15.3⋅ 1
V :=
⋅ ⋅( +
+
+
+
⋅
⋅ + ( + ⋅
⋅
1
P
0.741
0.616)
P
L
q
g)
L
2
l 1
0.869
w
2
2
V =
⋅
1
4797.82 kN
M :=
⋅
1
0kN m
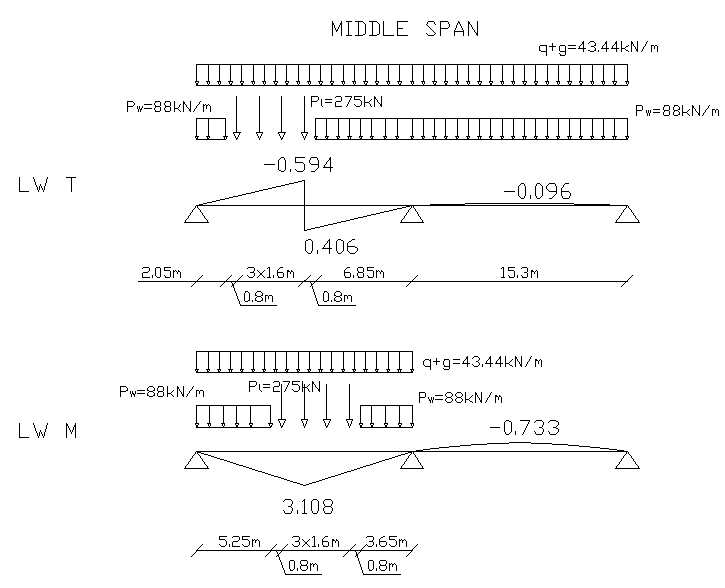
STEEL RAILWAY BRIDGE DESIGN
CROSS SECTION B - B
1
6.85 × 0.348
2.05⋅ 0.162
(−0.594 + 0.406)⋅15.3
V :=
⋅ −
⋅(
+
+
+
+
⋅
−
−
⋅ + ( + ⋅
−
⋅
2
P
0.276
0.381
0.485
0.594)
P
0.001 L
q
g)
0.001 L
2
l
w
2
2
4
V =
⋅
2
211.93 kN
1
5.25⋅2.029
3.65⋅ 1.224
2
15.3⋅ 3.108
2
M :=
⋅ ⋅(
+
+
+
⋅ +
⋅
+
⋅
+ ( + ⋅
⋅
2
P
2.295
1.557) L
P
L
q
g)
L
2
l 2.389
3.108
w
2
2
2
M =
⋅
⋅
2
48.42 MN m
1
5.25⋅2.029
3.65⋅ 1.224
2
M
:= ⋅ ⋅(
+
+
+
⋅ +
⋅
+
⋅
2uż
P
2.295
1.557) L
P
L
2
l 2.389
3.108
w
2
2
M
=
⋅
2uż
22.53 MN m
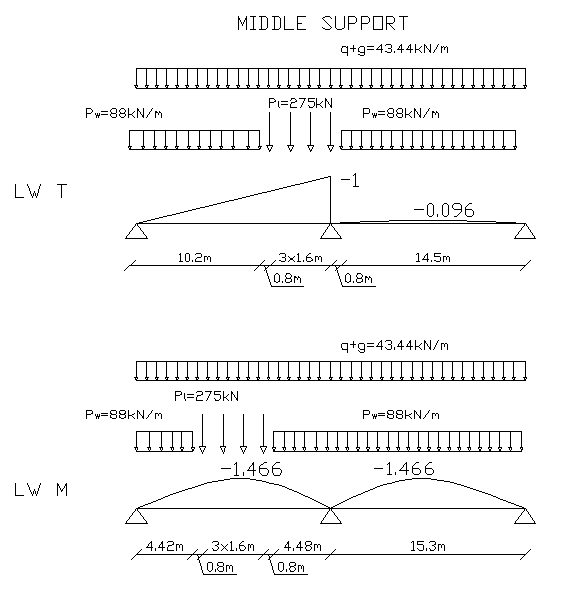
STEEL RAILWAY BRIDGE DESIGN
CROSS SECTION C - C
1
10.2 × 0.759
15.3⋅1
V :=
⋅ −
⋅(
+
+
+
−
⋅
+
⋅ − ( + ⋅
+
⋅
3
P
0.616
0.741
0.869
1)
P
0.001 L
q
g)
0.001 L
2
l
w
2
2
V = −
⋅
3
5592.629 kN
1
2
2
M :=
⋅ − ⋅(
+
+
+
⋅ −
⋅(
+
⋅
− ( + ⋅
⋅
3
P
1.147
1.363
1.466
1.42) L
P
) L
q
g) ( 0.03) L
2
l
w 0.003
0.015
M = −
⋅
⋅
3
11.69 MN m
STEEL RAILWAY BRIDGE DESIGN
2. Calculations 2.1. Steel parameters:
- Type: 18G2A
- Bending strength (in chords) R := 280MPa
- Shear strength (in web) R :=
t
170MPa
f :=
d
285MPa
h := 1.91m
E := 205GPa
h
:=
:=
:=
w
1.860m
bf
0.5m
bftop
2.830m
t
:=
:=
⋅
:=
⋅
w
0.02m
hf
0.03 m
hftop
0.02 m
2.2. Geometrical parameters of the profile Moment of inertia: 4
I :=
x
0.2m
First moment of inertia: 3
S := 0.022m
Ix
Bending indicator: 3
W :=
=
⋅
x
0.209 m
h
2.3. Stresses
2
2.3.1. Cross section A-A V ⋅
1 S
τ
:=
=
⋅
<
=
⋅
A
26.39 MPa
R
I ⋅
t
170 MPa
x tw
2.3.2. Cross section B-B
- shear stresses V ⋅
2 S
τ
:=
=
⋅
<
=
⋅
B
1.17 MPa
R
I ⋅
t
170 MPa
x tw
- bending stresses M2
σ
:=
=
⋅
<
=
⋅
B
231.21 MPa
R
280 MPa
Wx
- total stresses 2
2
τ
+
=
⋅
<
⋅ =
⋅
B
σB
231.21 MPa
1.1 R
308 MPa
2.3.3. Cross section C-C
- shear stresses V
⋅
3 S
τ
:=
=
⋅
=
⋅
C
39.54 MPa
R
I ⋅
<
t
170 MPa
x tw
- bending stresses M3
σ
:=
=
⋅
<
=
⋅
C
55.82 MPa
R
280 MPa
Wx
- total stresses 2
2
τ
+
=
⋅
<
⋅ =
⋅
C
σC
68.4 MPa
1.1 R
308 MPa
2.4 Checking of deflection 2
⋅
5
M2uż L
L
f :=
⋅
= 0.002 m
<
f
:=
= 0.026 m
348
E⋅ I
dop
x
600
V := −
3
7188.43
M :=
⋅
2
48.42MN m
M
:=
⋅
2uż
22.53MN m
M := −
3
1151726.47
V := −
3
7188.43
11
4
4
2⋅ 10 mm = 0.2 m 3
3
3
b
⋅
⋅
⋅
ftop hftop
bf hf
t
2
w hw
I :=
+
+
⋅ ⋅
+
x
2h
( 0.885m)
12
12
f bf
12
7
3
S := b
( ⋅ +
⋅
+
⋅ )⋅
=
×
⋅
f hf
bftop hftop hw tw 400mm 4.352
10 mm
2
3
S := 67053.0442mm ⋅ 322.3528mm = 0.022⋅ m
7188.43kN
1151726.47kN⋅ m
7188.43kN