GEODEZJA WYŻSZA I ASTRONOMIA GEODEZYJNA Ćwiczenie nr 5

Imię i nazwisko . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

N - ……. M - ………

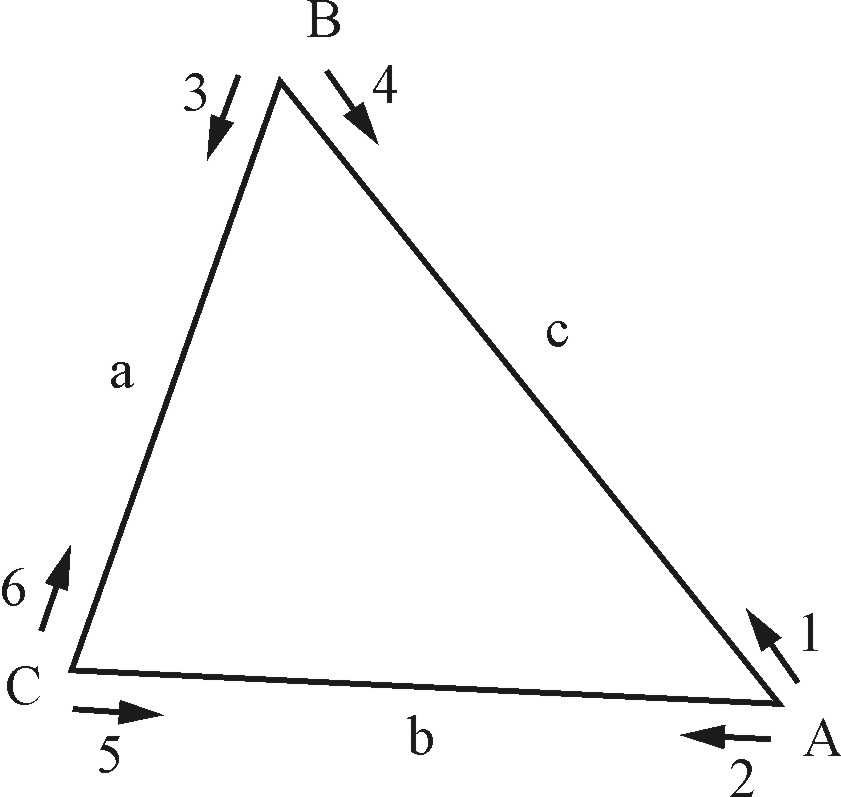
Na rysunku przedstawiony jest szkic sieci. Dane są współrzędne punktu C (z poprzedniego zadania) w odwzorowaniu Gaussa-Krugera. Na podstawie podanych azymutów boków wyznaczyć współrzędne przybliżone pozostałych punktów oraz wykonać redukcję kierunków i długości boków na płaszczyznę Gaussa-Krugera. Współrzędne do obliczenia redukcji należy brać w km.

Nr

Kąty

Azymuty

D

punktu

wierzchołkowe

C

10o6′ 2

2 ′

32738,5

A

314o20 2

′ 1′

144o26 5

′ 0′ 41011,4

B

307o45′04 ′

272o 2

1 0

′ ′

29613,9

C

277o54 3

′ 8′

o

10 6′ 2

2 ′

1. Obliczenie współrzędnych przybliżonych.

Y

∆ = sin A⋅ D

X

∆ = cos A⋅ D

Nr

sin A

∆

cos

∆

punktu

Y

Y

A

X

X

C

A

B

2. Redukcja kierunków δ = 0,

0 008439∗( x − x ∗ 2 y + y 2

1 )

( 1 2)

Kierunki

Kierunki zredukowane Nr.

δ

Kąty zredukowane

Stan.

zaobserwowane

kier

°

′

″

″

°

′

″

°

′

″

2

167

46

10

A

1

213

25

50

4

157

16

27

B

3

209

31

23

6

166

34

43

C

5

248

40

5

3. Redukcja długości D = ( x − x

+ y − y 1

)2

2

( 1

)2

2

d = D{1+ 0

,

0 0000000409( 2

2

y + y y + y 1

1

2

2 )}

Nr

D

d

boku

km

m

a

b

c

UWAGA!!!! Do obliczenia redukcji długości i kierunków współrzędne x i y bierzemy w km.