31.01.2014

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 75 min.

Nazwisko Imię Podpis Nr

albumu

Grupa

Sala

Uwaga. Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

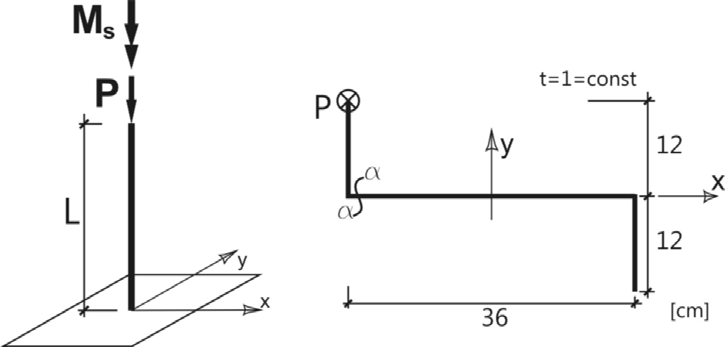
Zadanie 1 (20 punktów) Słup wspornikowy o wysokości L = 3 m i przekroju cienkościennym zetowym jak na rys. obciążony jest siłą P

i momentem M

= 200 MPa.

s. Stałe materiałowe: E = 200 GPa, ν = 0.25, granica proporcjonalności Rpr W punktach 1, 3 i 4 przyjąć P = 120 kN, Ms = 0.5 kNm, 1)

Podać funkcje i wykresy: osi obojętnej i naprężeń normalnych w przekroju, zachowując zwroty N ⎛

uI − vI

vI − uI

⎞

centralnych osi x, y wg rysunku. Zastosować wzór: σ ( x, y) =

⎜1

x

xy

y

xy

+

Ax +

Ay ⎟

2

2

A ⎜

I I

I

I I

I

⎟

−

−

⎝

x

y

xy

x

y

xy

⎠

2) Wyznaczyć rdzeń przekroju (współrzędne wierzchołków, rysunek) bok

y = a x + b a ≠

b ≠

y = b ≠

x ∈ −∞ +∞)

x = c ≠

y ∈ −∞ +∞)

wierzchołek

i

i ,

0

i

,

0

i

0

i

,

(

,

0

i

,

(

,

u

a J − J

b A

− J

b A

− J c A

i

(

) /

i

y

xy

i

/

xy

i

/

y

i

v

a J − J

b A

− J b A

− J

c A

i

(

) /

i

xy

x

i

/

x

i

xy

i

3) Przyjmując założenia skręcania swobodnego obliczyć maksymalne naprężenia styczne oraz maksymalny kąt skręcenia.

4) Obliczyć naprężenia zredukowane wg hipotezy H-M-H w p. α – α przekroju u podstawy słupa, wpływ skręcania – przyjąć w p. α – α naprężenia maksymalne 5) Rozpatrując stan idealnego ściskania osiowego obliczyć siłę krytyczną wyboczenia giętnego pręta, na rysunku przekroju poprzecznego zaznaczyć ślad płaszczyzny wyboczenia. Sprawdzić warunek wyboczenia sprężystego.

____________________________________________________________________________________________________________________________________

J.Ch. & W.W. / M.S. & M.G. 2014

Zadania WM_Egz0C_ZADANIA_14.doc