Chemia hydrosfery

Charakterystyka wody jako substancji chemicznej

W strukturze wody ciekłej występują cząsteczki wody zagregowane przez wiązania wodorowe, czyli w postaci multimerów asocjacyjnych. Średnie liczby cząsteczek wody, wchodzących w skład multimeru zostały w Tabeli 1 zestawione z temperaturami wody. Długość wiązania O-H, w zależności od warunków waha się w granicach 80 - 100 pm, podczas gdy długość wiązania wodorowego O......H wynosi ok. 180 - 280 pm. Energie ww oddziaływań są następujące: kJ

∆

kJ

H

= 463 5

,

∆ H

= 10 − 40

O-H

mol

O....H

mol

Zrywanie wiązań wodorowych pozwala na efektywniejsze upakowanie cząsteczek, co skutkuje zwiększeniem gęstości. W wyniku topnienia lodu ok. 12 % wiązań wodorowych ulega rozerwaniu.

skutkiem tego jest zwiększenie gęstości. Gęstość lodu wynosi 0,917 g/cm3, podczas gdy maksymalna gęstość wody występuje w temperaturze +4oC i wynosi 1 g/cm3. Wzrostowi gęstości na skutek zrywania wiązań wodorowych w wodzie ciekłej przeciwstawia się rozszerzanie termiczne, które uzyskuje przewagę nad poprzednim efektem w temperaturze powyżej +4oC.

Tabela 1. Liczba cząsteczek w zasocjowanym agregacie (multimerze asocjacyjnym) Temperatura

Liczba cząsteczek

0oC

~100

25oC

90

70oC

25

100oC

max. 6

Dzięki tak dużej energii wiązania wodorowego występującego w strukturze zarówno wody ciekłej jak i lodu, woda jest substancją charakteryzującą się wyjątkowo dużymi wartościami entalpii przemian fazowych. Entalpie topnienia lodu i parowania wody wraz z równaniami tych przemian zostały przedstawione w postaci równań (1) i (2):

kJ

H

∆ H =

2O(s)

H2O(c)

,

6 02

(1)

mol

kJ

H

∆ H =

2O(c)

H2O(g)

4 ,

0 6

(2)

mol

Właściwości utleniająco–redukujące wody można scharakteryzować opisem potencjału procesów utleniania i redukcji wody. Utlenianie wody (równanie (3)) prowadzi do wydzielania tlenu: 2H2O

O2(g) + 4H+(aq) + 4e-

(3)

Potencjał dla reakcji utleniania wody można opisać zmodyfikowanym równaniem Nernsta (równanie (4)) słusznym dla układów o temperaturze 25oC:

E

(4)

O

= ,

1 23 − 0

,

0 591⋅ pH

2 2H O

2

Redukcja wody (równanie (5)) prowadzi do wydzielania wodoru:

2H2O + 2e-

H2(g) + 2OH-(aq)

(5)

1

Potencjał dla reakcji redukcji wody można opisać zmodyfikowanym równaniem Nernsta (równanie (6)) słusznym dla układów o temperaturze 25oC:

E

(6)

2H O

= − 0

,

0 591⋅ pH

2

H2

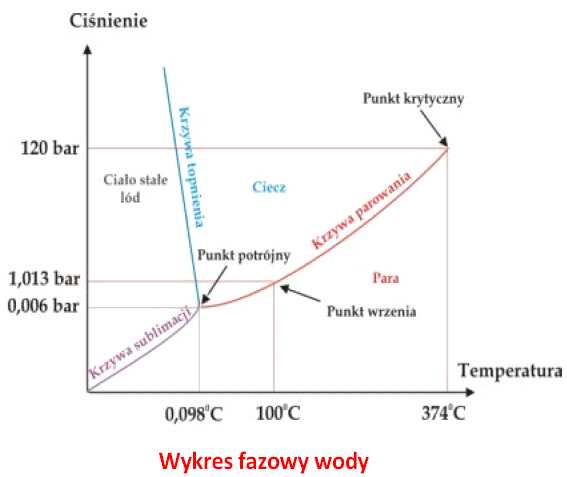
Diagram fazowy wody zawierający punkt

potrójny i punkt krytyczny został przedstawiony

na Rys. 1.

Właściwości wody związane z równowagami

jonowymi w roztworach wodnych zostały

omówione na wykładzie.

Woda jest zasadą Lewisa i może tworzyć z

jonami metali, które posiadają nie zapełnione

orbitale d akwakompleksy. Kompleksy te nie są

najtrwalsze i dlatego możliwe jest istnienie

jonów metali w środowisku wodnym w postaci

różnych kompleksów zarówno jonowych jak i

obojętnych.

Rys. 1. Wykres fazowy wody

Wody oceaniczne

97 % wody znajdującej się na Ziemi, to oceany. Ze względu na zróżnicowany charakter środowiska na różnych głębokościach można w oceanie wyróżnić następujące warstwy:

1. Mikrowarstwa powierzchniowa (kilka µm)

- zawiera związki niskopolarne, m.in. organiczne związki powierzchniowo czynne, chelaty wewnętrzne metali, substancje oleiste

- skład morskich aerozoli jest silnie związany ze składem mikrowarstwy

2. Warstwa zmieszana (do 300 m)

- makro- i mikroelementy zużywane przez fitoplankton (np. azot i miedź)

- substancje pochodzące z atmosfery (np. wanad i ołów)

3. Metalimnion – termoklina (do kilkuset m)

- warstwa charakteryzująca się stałym spadkiem temperatury

4. Głębiny oceaniczne (do równin abysalnych i dna rowów oceanicznych)

- wymiana wody z warstwami wyższymi odbywa się bardzo wolno

Woda słodka

Woda słodka stanowi ok. 3 % globalnych zasobów wody. Ok. ¾ wody słodkiej znajduje się w polarnych czapach lodowych i górskich lodowcach, z czego 90 % przypada na lądolód antarktyczny. Ok. 20 % zasobów wody słodkiej stanowi woda gruntowa. Ok. 0,5 % wody słodkiej stanowią wody powierzchniowe, tj. rzeki i jeziora. Woda zawarta w atmosferze jest równoważna 15 % wody zawartej w rzekach i jeziorach.

W ciepłej porze roku (latem) można wyróżnić w jeziorze 3 warstwy analogiczne do warstw wód oceanicznych:

- epilimnion (spadek temperatury wraz z głębokością)

- metalimnion

- hipolimnion

W okresie końca pory ciepłej następuje ochłodzenie warstwy powierzchniowej, co prowadzi do opadania wody dobrze napowietrzonej i bogatej w składniki pokarmowe i wynoszenia ku powierzchni wody z warstw głębszych. Proces mieszania określa się mianem inwersji warstw.

2

W okresie zimy na powierzchni jezior pojawia się lód, a temperatura wody wzrasta ku dołowi maksymalnie do 4oC. Głębokie warstwy jezior, których temperatura wynosi zawsze 4oC nazywane są termokliną.

W okresie wiosny ponownie dochodzi do mieszania warstw, a następnie do ustalenia warstwowej struktury typowej dla lata i cykl się zamyka.

Rozpuszczanie gazów w wodach

W przypadku gazów nie reagujących z wodą do opisu równowagi pomiędzy gazem w atmosferze i gazem rozpuszczonym w wodzie można zastosować prawo Henry’ego (równanie (7)).

[g] = k ⋅ p

(7)

H

g

gdzie:

 mol

[g] – stężenie gazu rozpuszczonego w wodzie 



 L 

 mol 

kH – stała Henry’ego 



 L ⋅ Pa 

pg – ciśnienie parcjalne gazy w atmosferze [Pa]

Tabela 2. Wartości stałej Henry’ego dla wybranych gazów rozpuszczonych w wodzie w temperaturze 25oC, dla postaci prawa: [g] = k ⋅ p

H

g

 mol 

Gaz

k

H 



 L ⋅ Pa 

O

−

2

8

3

,

1 ⋅10

N

−

2

9

,

6 4 ⋅10

CH

−

4

8

3

,

1 ⋅10

CO

−

2

7

3

,

3 ⋅10

SO

−

2

5

8

,

1 ⋅10

NH

−

3

4

,

5 7 ⋅10

Hg

7

,

8 6 10−

⋅

CCl

−

4

7

,

3 7 ⋅10

CH

−

3COCH3

3

9

,

3 ⋅10

Ciśnienie cząstkowe (parcjalne) gazu w atmosferze można zdefiniować za pomocą równania (8): p = p 0 ⋅ x

(8)

j

j

gdzie:

pj – ciśnienie parcjalne gazu j

p 0 – ciśnienie atmosferyczne

3

xj – ułamek molowy gazu j w atmosferze

Ciśnienia parcjalne składników każdej mieszaniny gazowej spełniają prawo Daltona (równanie (9)): p = p 1 + p 2 + p + ...

3

+ p

p

i = ∑

i

i

(9)

gdzie:

p – ciśnienie całkowite w mieszaninie gazów

p 1, p 2, p 3, ..., pi – ciśnienia parcjalne poszczególnych składników mieszaniny gazowej (1,2,3, ..., i) Zawartości składników atmosfery mogą być określone za pomocą ułamków molowych poszczególnych jej składników w odniesieniu do suchego powietrza dlatego, że zawartość pary wodnej jest zmienna. Prężność pary wodnej (pary nasyconej) będąca jednocześnie jej ciśnieniem parcjalnym nad lustrem wody zależy od temperatury. Prężność pary nasyconej cieczy i [Pa] można obliczyć korzystając z równania (10):

− H par

∆ i

RT

p = C ⋅ e

(10)

i

i

gdzie:

pi – prężność pary nasyconej cieczy i [Pa]

Ci – stała

par

H

∆

– ciepło parowania cieczy i

i



J



R – stała gazowa  3

,

8 145





mol ⋅ K 

T – temperatura bezwzględna

Ze względu na to, że ciepło parowania zależy od temperatury, znacznie lepiej jest w przypadku wody skorzystać z półempirycznego równania opisującego zależność prężności pary nasyconej od temperatury (równanie (11)):

17,5043 t

⋅

o

24 ,

1 2+ t

p t

( ) = p(0 C) ⋅ e

(11)

gdzie:

p( t) – ciśnienie pary nasyconej w temperaturze t

p(0oC) – ciśnienie pary nasyconej w temperaturze 0oC (611,2 Pa)

t – temperatura [oC]

Uwzględniając wkład pary wodnej w ciśnienie atmosferyczne możemy obliczyć ciśnienie parcjalne wybranego gazu wchodzącego w skład atmosfery. W przypadku tlenu, jego ciśnienie parcjalne w atmosferze wynosi (równanie (12)):

0

p

= ( p − p

) x

(12)

O2

H2O

O2

Dane potrzebne do obliczenia ciśnienia cząstkowego tlenu lub azotu w warunkach pary nasyconej w temperaturze 25oC zostały zestawione w Tabeli (3). Stężenie tlenu w wodzie można obliczyć z prawa Henry’ego dla tlenu (równanie (7a)):

[O ] = k ⋅ p

(7a)

2

H

O2

−4 mol

mg

Zatem dla 25oC równowagowa zawartość tlenu w wodzie wynosi: [O ] = ,

2 7 ⋅10

= 5

,

8

2

L

L

4

Tabela 3. Dane potrzebne do obliczenia ciśnienia cząstkowego tlenu lub azotu w warunkach pary nasyconej w temperaturze 25oC

xj w suchym powietrzu

p

H O

2

N2 – 0,78

O2 – 0,209

25oC – 3200 Pa

inne ~ 0,01

Podczas obliczania zawartości tlenu w wodzie w innych temperaturach należy uwzględnić wpływ temperatury zarówno na prężność pary wodnej, jak i na wartość stałej Henry’ego. Wyniki obliczeń równowagowej zawartości tlenu w wodzie w różnych temperaturach zestawione zostały w Tabeli 4.

Tabela 4. Równowagowa zawartość tlenu w wodzie w różnych temperaturach

Temperatura

[O2]

5oC

12,4 ppm

25oC

8,5 ppm

30oC

7,5 ppm

Równowagowe stężenie tlenu w wodach słonych, np. w powierzchniowych warstwach wód oceanicznych można obliczać na podstawie półempirycznego równania Bensona i Krausego, które uwzglednia zasolenie (równanie (13)):

B

C

D

E



G

H 

ln C

A

S F

(13)

O

= + +

+

+

−  +

+



2

2

3

4

T

T

T

T



2

T

T 

gdzie:

C O – stężenie ditlenu [µmol/kg]

2

T – temperatura bezwzględna [K],

S – zasolenie [‰],

A = -1,3529996·102,

B = 1,572288·105,

C = -6,637149·107,

D = 1,243678·1010,

E = -8,621061·1011,

F = 2,0573·10-2,

G = -1,2142·101,

H = 2,3631·103.

Przedstawiony przykład tlenu odzwierciedla możliwości ilościowego opisu rozpuszczania w wodzie gazów nie reagujących z wodą. W przypadku gazów, które podczas rozpuszczania w wodzie wchodzą z nią w reakcję, opis równowagi z atmosferą musi dodatkowo uwzględniać równowagi chemiczne odnoszące się do odpowiednich reakcji.

5

Przykładem gazu będącego bezwodnikiem kwasowym, a więc reagującym z wodą jest ditlenek węgla. Do opisu równowagi pomiędzy dwutlenkiem węgla zawartym w powietrzu, a tym który jest rozpuszczony w wodzie w stanie niezmienionym chemicznie można zastosować prawo Henry’ego.

Równowagę tę można przedstawić za pomocą równania (14):

CO2(g)

CO2(aq)

(14)

Przyjmując, że zawartość CO2 w suchej atmosferze w temperaturze 25oC wyrażona w postaci ułamka molowego wynosi

4

x

= 7

,

3 8 10−

⋅

obliczamy jego ciśnienie parcjalne z uwzględnieniem

CO2

ciśnienia parcjalnego nasyconej pary wodnej (równanie (15)):

p

= p − p

⋅

=

⋅

−

⋅

⋅

⋅ −

x

=

(15)

2

( 0

CO

H O

2

) CO2 ( 0,

1 125 105 Pa

,

3 2 103 Pa) 7

,

3 8 10 4

36 9

, Pa

Jako że stała Henry’ego ditlenku węgla w temperaturze 25oC wynosi:

[CO ]

2

−7

k

=

= 3

,

3 ⋅10

(16)

H

p CO2

stężenie ditlenku węgla w wodzie w stanie niezmienionym chemicznie, [CO2] obliczamy z prawa Henry’ego (równanie (17)):

−7 mol

−5 mol

[CO ] = k ⋅ p

= 3

,

3 ⋅10

⋅ ,

3 69Pa = ,

1 2 ⋅10

(17)

2

H

CO2

L ⋅ Pa

L

Stężenie pozostałych form ditlenku węgla rozpuszczonych w wodzie obliczamy z uwzględnieniem stężenia jonów hydroniowych i stałych odpowiednich równowag jonowych (równania (18) – (21)):

[H CO ]

CO

2

3

−

K

(18)

r =

= ⋅

2(aq) + H2O

H2CO3

3

2 10

[CO ]

2

-

[HCO ][H O+ ]

H

-

3

3

−

K

(19)

a =

= ⋅

2CO3 + H2O

HCO3 + H3O+

4

'

2 10

1

[H CO ]

2

3

2-

[CO ][H O+ ]

HCO -

2-

3

3

−

K

(20)

a

=

=

⋅

3 + H2O

CO3 + H3O+

11

7

,

4

10

2

-

[HCO ]

3

-

[HCO ][H O+ ]

CO

-

3

3

−

K

K

K

(21)

a

= a ⋅ r =

=

⋅

2(aq) + 2H2O

HCO3 + H3O+

7

'

5

,

4

10

1

1

[CO ]

2

Jednym z ważniejszych odbiorników ditlenku węgla w procesach naturalnych są zawarte w wodach kationy wapnia Ca2+. Warunek elektroobojętności roztworu wodnego zawierającego jony wapnia można zapisać w postaci równania (22):

2[Ca2+] + [H

-

2-

3O+] = [HCO3 ] + 2[CO3 ] + [OH-]

(22)

Ponadto w zakresie pH = 6 ÷ 9 spełnione są następujące silne nierówności:

[H3O+] << [Ca2+]

[CO 2-

-

3 ] << [HCO3 ]

[OH-] << [HCO -

3 ]

a zatem warunek elektroobojętności można uprościć (równanie (23)):

2[Ca2+] = [HCO -

3 ]

(23)

Stężenie równowagowe poszczególnych form ditlenku węgla w wodzie obliczamy na podstawie następujących zależności:

6

[CO2- ][H O+ ]

K [HCO- ]

3

3

K

=>

[CO2- ]

2

3

= a

(20a)

a

=

2

3

[HCO- ]

[H O+ ]

3

3

[HCO- ][H O+ ]

K [CO ]

3

3

K

=>

[HCO- ]

1

2

= a

(21a)

a

=

1

[CO ]

3

[H O+ ]

2

3

K [CO ]

1

a

2

K a 2 [H O+]

K K [CO ]

2-

3

a 2

1

a

2

[CO ] =

=

(24)

3

+

+ 2

[H O ]

[H O ]

3

3

[CO ]

2

k =

=>

[CO ] = k p

(16a)

H

p

2

H

CO2

CO2

K K k

2-

a 2

1

a

H

CO

[CO ]

2

=

p

(25)

3

+ 2

[H O ]

3

[H O+ ] = ?

3

Równowagi jonowe w wodach zawierających jony wapnia związane z ich stężeniem oraz stężeniami jonów hydroniowych i różnych form ditlenku węgla można przedstawić za pomocą obliczeń podzielonych na poszczególne zagadnienia:

1. Obliczanie stężenia [Ca2+]

Podstawową zależnością wiążącą stężenia jonów wapnia i jonów węglanowych w wodzie jest iloczyn rozpuszczalności węglanu wapnia:

L

2+

2−

9

L

= [Ca ] C

[ O ] = 5⋅10−

=>

[Ca 2+ ]

CaCO3

=

(26)

CaCO

3

3

[CO2− ]

3

Podstawiając równanie (25) do równania (26) otrzymujemy zależność:

+ 2

L

L

⋅[H O ]

2+

CaCO

CaCO

3

3

3

[Ca ] =

=

(27)

K

⋅ K ⋅ k ⋅ p

⋅

⋅ ⋅

a 2

1

a

H

CO

K

K

k

p

2

1

a

a 2

H

CO2

+ 2

[H O ]

3

[H O+ ] = ?

3

2. Obliczanie stężenia [HCO -

3 ]

[HCO- ][H O+ ]

K

-

[CO ]

3

3

K

=>

[HCO ]

1

2

= a

(21a)

a

=

1

[CO ]

3

[H O+ ]

2

3

Podstawiając równanie (16a) do równania (21a) otrzymujemy zależność:

Ka ⋅

Ka ⋅ k ⋅ p

-

[CO ]

[HCO ]

1

H

CO

1

2

2

=

=

(28)

3

[H O+ ]

[H O+ ]

3

3

2[Ca2+] = [HCO -

3 ]

<- warunek elektroobojętności

(23)

Podstawiając równanie (27) do uproszczonego warunku elektroobojętności (równanie (23)) otrzymujemy zależność:

7

+ 2

2 ⋅ L

⋅[H O ]

-

CaCO3

3

[HCO ] =

(29)

3

K ⋅ K ⋅ k ⋅ p

1

a

a 2

H

CO2

[H O+ ] = ?

3

3. Obliczanie pH wody w obecności wapieni

Porównując prawe strony równań (28) i (29) otrzymujemy następującą zależność:

+ 2

K ⋅ k ⋅ p

2 ⋅ L

⋅[H O ]

1

a

H

CO

CaCO

3

2

3

=

[H O+

(30)

]

K ⋅ K ⋅ k ⋅ p

3

1

a

a 2

H

CO2

która pozwala na obliczenie zawartości jonów hydronionych w wodach zawierających jony wapnia w zależności od ciśnienia parcjalnego ditlenku węgla w atmosferze:

2

2

2

K ⋅ K ⋅ k ⋅ p

2

2

2

K ⋅ K ⋅ k ⋅ p

+ 3

1

a

a 2

H

CO

+

1

a

a 2

H

CO

2

[H O ] =

=>

2

[H O ] = 3

(31)

3

2 ⋅ L

3

2 ⋅ L

CaCO

CaCO

3

3

Do obliczeń przyjmujemy następujące dane dla temperatury 25oC, warunków pary nasyconej i standardowego ciśnienia atmosferycznego:

p

= p − p

⋅

=

⋅

−

⋅

⋅

⋅ −

x

=

2

( 0

CO

H O

2

) CO2 ( 0,

1 125 105 Pa

,

3 2 103 Pa) 7

,

3 8 10 4

36 9

, Pa

7

k = 3

,

3

10−

⋅

1

− 1

K

7

K

9

L

= 5 10−

⋅

a

= 5

,

4

10−

⋅

a

= ,

4 7 ⋅10

H

2

1

CaCO3

Obliczamy pH dla powyższych danych:

2

2

−7

1

− 1

−7

2

+

⋅

⋅

⋅

⋅

⋅

⋅

3 (

5

,

4

10 )

7

,

4

10

( 3,

3

10 ) (36 9

, )

−9 mol

[H O ] =

= ,

5 2 ⋅10

3

2 ⋅ 5⋅10−9

L

= −log[H O+

pH

] = 3

,

8

3

4. Obliczanie stężenia [HCO -

3 ] dla pH = 8,3

+

−9 mol

p

= 36 9

, Pa

7

k = 3

,

3

10−

⋅

7

K

[H O ] = ,

5 2 ⋅10

a

= 5

,

4

10−

⋅

CO2

H

1

3

L

Podstawiając

powyższe

dane

do

równania (28)

obliczamy

stężenie

anionów

wodorowęglanowych w wodach zawierających jony wapnia:

−

−

K a ⋅ k ⋅ p

⋅

⋅

⋅

⋅

-

1

H

CO

5

,

4

10 7

3

,

3

10 7 36 9

,

2

−3 mol

[HCO ] =

=

= ,

1 05 ⋅10

3

[H O+ ]

,

5 2 ⋅10−9

L

3

5. Obliczanie stężenia [CO 2-

3 ] dla pH = 8,3:

p

= 36 9

, Pa

−7

k = 3

,

3 ⋅10

−7

K

−11

K

a

= ,

4 7 ⋅10

a

= 5

,

4 ⋅10

CO2

H

1

2

+

−9 mol

[H O ] = ,

5 2 ⋅10

3

L

Podstawiając powyższe dane do równania (25) obliczamy stężenie anionów węglanowych w wodach zawierających jony wapnia:

8

−

−

−

K K k p

a

a

⋅

⋅

⋅

⋅

⋅

⋅

2-

2

1

H

CO

7

,

4

10 11

5

,

4

10 7

3

,

3

10 7 36 9

,

2

−6 mol

[CO ] =

=

=

⋅

3

[H O+ ]2

−

⋅

3

(

2

,

5 2 10 9 )

5

,

9

10

L

6. Obliczamy stężenie [Ca2+] dla pH = 8,3

p

= 36 9

, Pa

7

k = 3

,

3

10−

⋅

−7

K

−11

K

a

= ,

4 7 ⋅10

a

= 5

,

4 ⋅10

CO2

H

1

2

+

−9 mol

9

L

= 5 10−

⋅

[H O ] = ,

5 2 ⋅10

CaCO3

3

L

Podstawiając powyższe dane do równania (25) obliczamy stężenie kationów wapnia: L

⋅[H O+ ]2

2

−

−

⋅

⋅

⋅

CaCO

3

2+

5 10 9

3

( ,52 10 9)

−4 mol

[Ca

] =

=

= 3

,

5 ⋅10

K a ⋅ Ka ⋅ k ⋅ p

5

,

4 ⋅10−7 ⋅ ,

4 7 ⋅10 1

− 1 ⋅ 3

,

3 ⋅10−7 ⋅ 36 9

,

L

1

2

H

CO2

7. Obliczanie stężenie [Ca2+] bezpośrednio z iloczynu rozpuszczalności dla pH = 8,3

−

2-

−6 mol

9

L

= 5⋅10

[CO ] = 5

,

9 ⋅10

CaCO3

3

L

Podstawiając powyższe dane do równania (26) obliczamy stężenie kationów wapnia:

−

L

⋅

CaCO

2+

5 10 9

3

−4 mol

[Ca

] =

=

= 3

,

5 ⋅10

[CO2− ]

5

,

9 ⋅10−6

L

3

Przedstawione obliczenia pozwalają wyciągnąć następujące wnioski odnoszące się do wód zawierających jony wapnia:

• najwa

-

żniejszymi kationami w bilansie są jony Ca2+ i HCO3 ,

• pH roztworu wynosi 8,3,

• CO

2-

2 i CO3 występują w niewielkich stężeniach,

Zasadowość

Pojemność buforowa wody w stosunku do kwasów może być wyrażona za pomocą parametrów odzwierciedlających jej potencjalną zdolność do reagowania z czynnikami zakwaszającymi.

Zasadowość stanowi miarę zdolności wody do zobojętniania kwasów

zasadowosc = [OH− ] + [HCO− ] + [

2 CO2− ] −[H O+ ]

(32)

3

3

3

Innym parametrem podobnym do zasadowości jest zdolność zobojętniania kwasów (ANC - acid-neutralizing capacity):

ANC = [OH− ] + [HCO− ] + [

2 CO2− ] + [B(OH)− ] + [H SiO− ] + [HPO2− ] + [HS− ] + [NMO− ] + ...

3

3

4

3

4

4

(33)

... −[H O+ ] − [

3 A (

l H O)3+ ] − ...

3

2

6

gdzie: NMO – naturalna materia organiczna

Zasadowość i zdolność zobojętniania kwasów definiowane są jako różnice stężeń akceptorów i donorów protonów w wodzie. Oto niektóre reakcje przyłączania protonów, które mają potencjalne znaczenie w kreowaniu zdolności zobojętniania kwasów:

B(OH) -

4 + H3O+

H3BO3 + 2H2O

p Ka = 9,14

(34)

9

H

-

3SiO4 + H3O+

Si(OH)4 + H2O

p Ka = 9,66

(35)

HPO 2-

-

4 + H3O+

H2PO4 + H2O

p Ka = 7,21

(36)

HS- + H3O+

H2S + H2O

p Ka = 7,04

(37)

[Al(H2O)5OH]2+ + H3O+

[Al(H2O)6]3+ + H2O

(38)

[Al(H2O)4(OH)2]+ + H3O+

[Al(H2O)5OH]2+ + H2O

(39)

[Al(H2O)3(OH)3] + H3O+

[Al(H2O)4(OH)2]+ + H2O

(40)

W większości ekosystemów wodnych stężenia indywiduów uczestniczących w równowagach przedstawionych równaniami (34) – (40) są zbyt małe aby zdecydowanie mogły się one przyczyniać do buforowania kwasów. Dlatego też w większości zbiorników wodnych zasadowość jest równa ANC. Ze względu na duże znaczenie takich protonoakceptorów jak aniony węglanowe, wodorowęglanowe i wodorotlenowe, zbiorniki wodne, w podłożu których występuje wapień mają największą zasadowość. NMO charakteryzuje się zmiennym stężeniem w ekosystemach wodnych.

Jej znaczenie jest szczególnie duże w zbiornikach wodnych, w których nie występują inne czynniki protonoakceptorowe.

Stosunkowo prostą metodą wyznaczania zasadowości, a właściwie ANC (zdolności zobojętniania kwasów) jest miareczkowanie próbki wody roztworem mocnego kwasu. W trakcie miareczkowania, po „przebiciu” pojemności buforowej następuje zwykle skok wartości pH, związany z protonowaniem któregoś protonoakceptora.

10