UKŁADY DWUSKŁADNIKOWE
Zmienność dwuskładnikowego dwufazowego
układu wynosi z = 2
Z reguły faz Gibbsa
z = s – f + 2
można obliczyć liczbę stopni swobody równowagi termodynamicznej pomiędzy fazą
ciekłą i gazową
( równowaga ciecz – para nasycona, f=2 ) dla roztworów dwuskładnikowych s=2 .
Stan roztworu dwuskładnikowego określają parametry :
temperatura T
ciśnienie pary nasyconej każdego składnika p
1
oraz p
2
(prężności składników )
ciśnienie pary nasyconej roztworu ( prężność roztworu)
skład fazy ciekłej ( ułamki molowe składników w cieczy: x
1
i x
2
)
skład fazy gazowej ( ułamki molowe składników w parze: y
1
i y
2
)
Dowolnie możemy zmieniać tylko dwa parametry
( z=2)
,
np. temperaturę T i ułamek molowy jednego składnika w fazie
ciekłej x
i
na pozostałe parametry:
- stężenie drugiego składnika w
cieczy,
- skład fazy gazowej,
- prężności składników,
- prężność roztworu
nie mamy wpływu.
Rozważamy roztwory dwóch cieczy o nieograniczonej mieszalności w całym zakresie stężeń:
mamy więc układ z jedną
fazą ciekłą
i
fazą gazową
.
SPOSOBY OPISU SKŁADU FAZ
Skład układów dwuskładnikowych przedstawiamy za pomocą stężenia.
1. ułamki wagowe (% wagowe ) u
w - masa składnika
2.
ułamki molowe (% molowe ) x
3
. stężenie molowe (molowość) c
liczba moli substancji rozpuszczonej n
B
w 1 dm
3
(L) roztworu
4
. stężenie molalne ( molalność ) m
liczba moli substancji rozpuszczonej n
B
w 1kg rozpuszczalnika
w
A
masa rozpuszczalnika w kg
w
B
masa substancji rozpuszczonej w g
1
u
u
w
w
w
u
w
w
w
u
B
A
B
A
B
B
B
A
A
A
)
M
m
n
;
M
m
(n
1
x
x
n
n
n
x
n
n
n
x
B
B
B
A
A
A
B
A
B
A
B
B
B
A
A
A
]
dm
[mol
V
M
w
V
n
c
3
roztw
B
B
roztw
B
]
kg
[mol
w
M
1000
w
w
n
m
1
A
B
B
A
B
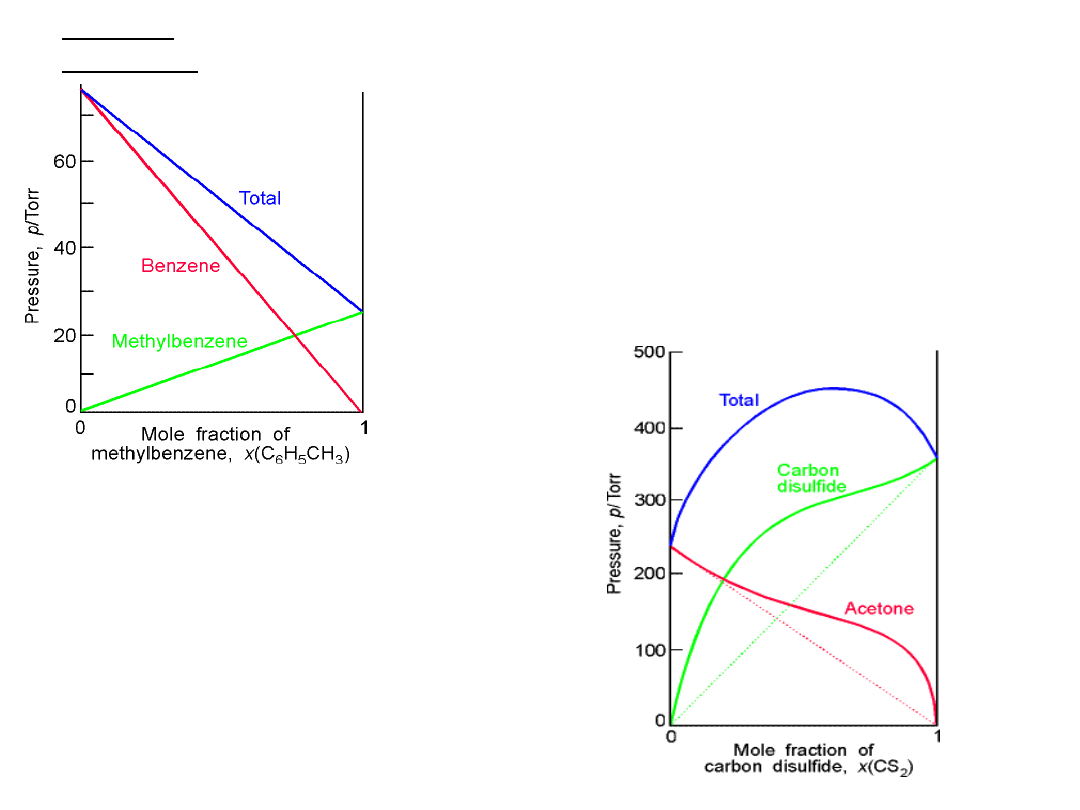
PRAWO
RAOULTA
Prawo Raoulta spełniają
roztwory podobnych cieczy np:
benzen i toluen.
tzw. roztwory doskonałe
(idealne)
Ciecze niepodobne chemicznie S=C=S i
CH
3
COCH
3
wykazują silne odchylenia od roztworu
idealnego
Prężność każdego składnika p
i
w stałej temperaturze w
zależności od składu roztworu określa prawo RAOULTA:
Prężność składnika p
i
jest proporcjonalna do ułamka
molowego składnika w roztworze x
i
.
p
A
= p
A
0
x
A
p
B
= p
B
0
x
B
Współczynnikiem proporcjonalności jest prężność
czystego składnika p
i
0
:
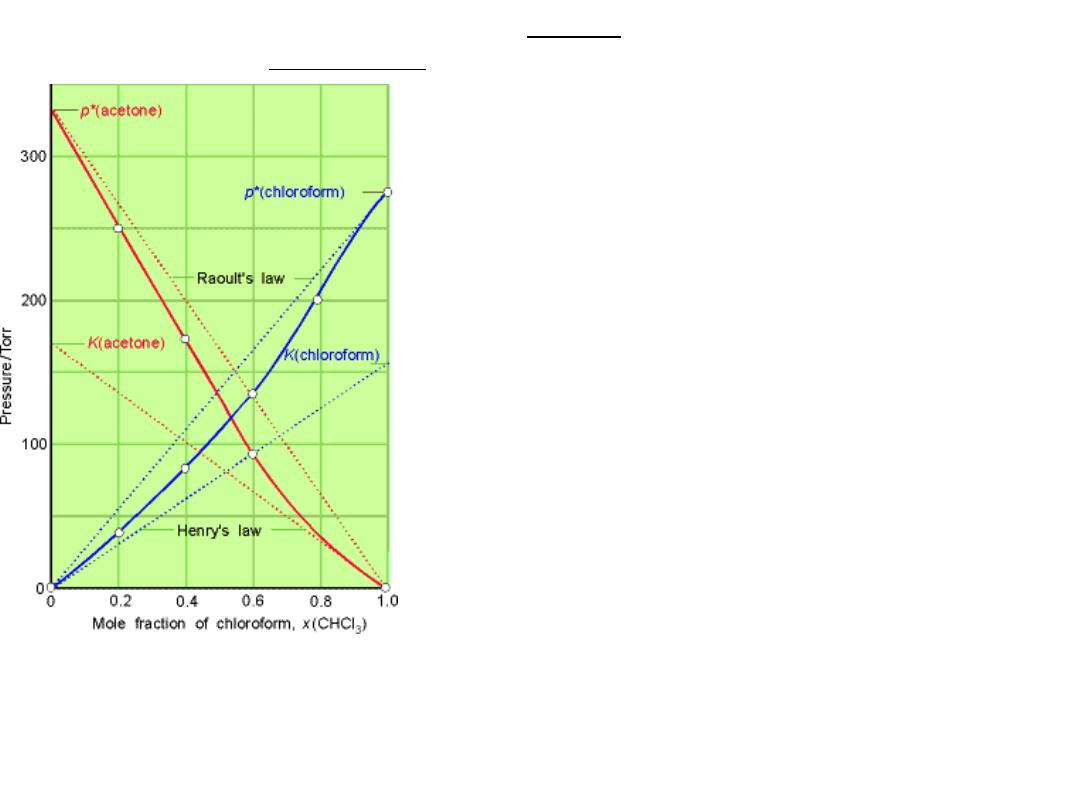
Roztwory idealne rozcieńczone - prawo
Henry’ego
William Henry wykazał doświadczalnie, że
dla roztworów rzeczywistych o małym stężeniu,
prężność pary substancji rozpuszczonej (B) jest
proporcjonalna do jej ułamka molowego :
p
B
= K
B
x
B
K
B
– stała Henry’ego,
jest stałą empiryczną, ma
wymiar ciśnienia,
a jej wartość dobiera się tak,
aby wykres prężności pary
składnika B
w funkcji ułamka molowego
x
B
był styczny
do krzywej doświadczalnej w
punkcie x
B
= 0
Mieszaniny,
w których substancja rozpuszczona (B) spełnia
rawo Henry’ego,
a rozpuszczalnik (A) spełnia prawo Raoulta,
nazywamy
roztworami idealnymi
rozcieńczonymi.
Potencjał chemiczny składnika w roztworze
doskonałym.
Potencjał chemiczny składnika w fazie gazowej dla T=const:
o
i
g
o
i
g
i
p
p
RTln
)
(μ
)
(μ
Z prawa Raoulta:
i
x
p
p
o
i
i
stąd
o
i
o
i
g
o
i
g
i
p
x
p
RTln
)
(μ
)
(μ
Z warunku równowagi:
c
i
g
i
)
(
)
(
otrzymujemy potencjał chemiczny składnika w roztworze:
i
o
o
i
g
o
i
c
i
RTlnx
p
p
RTln
)
(μ
)
(μ
Ponieważ potencjał standardowy ciekłego składnika (
i
o
)
c
jest równy:
o
o
i
g
o
i
c
o
i
p
p
RTln
)
(μ
)
(μ
Potencjał chemiczny składnika w roztworze doskonałym jest
liniową funkcją logarytmu ułamka molowego składnika w
roztworze.
i
c
o
i
c
i
RTlnx
)
(μ
)
(μ
otrzymujemy:
Potencjał chemiczny składnika w roztworze
niedoskonałym.
)
x
RTln(
γ
)
(μ
μ
i
i
c
o
i
i
W roztworach niedoskonałych występują różne oddziaływania pomiędzy
składnikami w wyniku, których roztwory te nie spełniają prawa Raoulta
x
p
p
i
o
i
i
W wyrażeniu opisującym potencjał chemiczny
składnika roztworu rzeczywistego zamiast ułamka
molowego składnika uwzględniamy
efektywne
stężenie składnika
nazwane
termodynamiczną aktywnością składnika:
a
i
=
i
x
i
i
c
o
i
c
i
RTlna
)
(μ
)
(μ
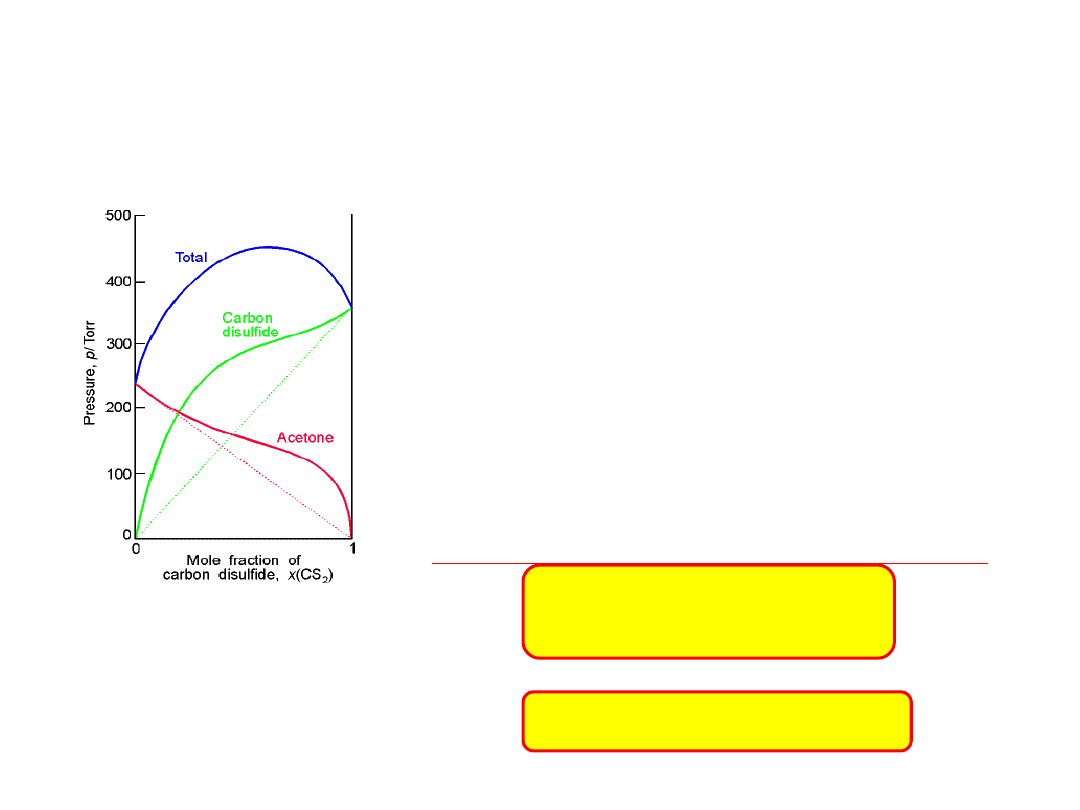
Roztwór cechuje maksimum prężności oraz
minimum temperatury wrzenia.
Silne odpychanie cząsteczek
różnoimiennych powoduje, że prężności
obu składników są większe od
oczekiwanych.
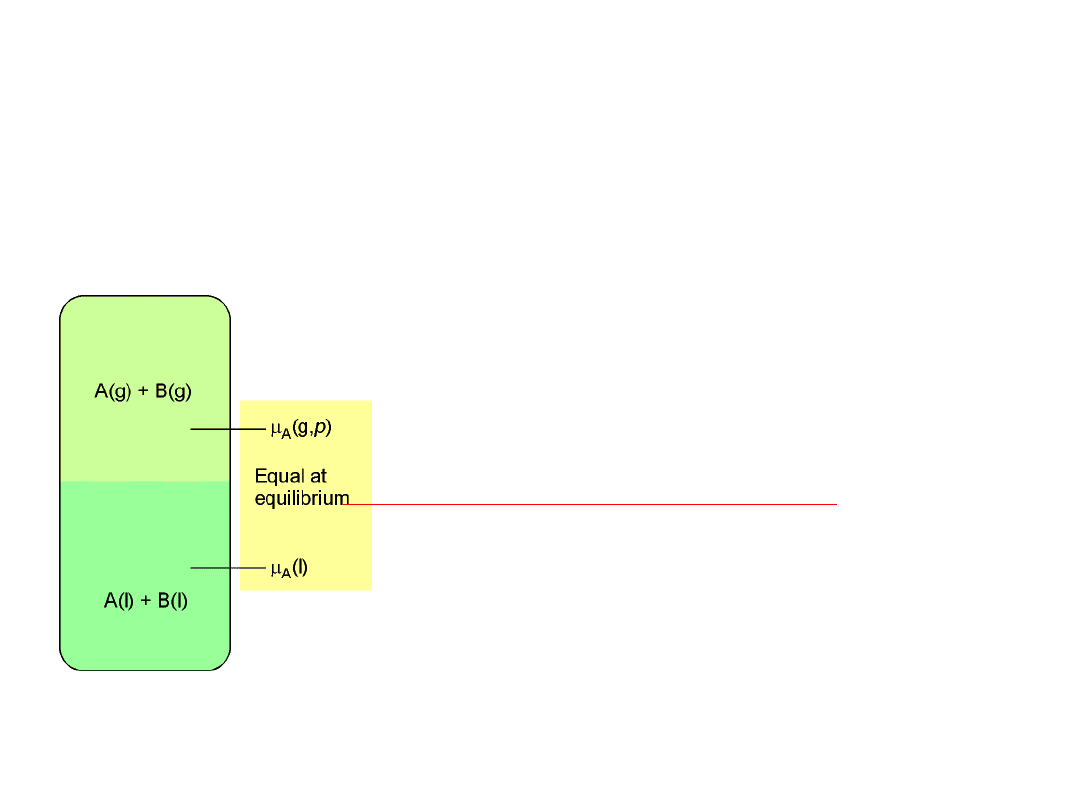
Termodynamika ciekłych układów
dwuskładnikowych
(termodynamika roztworów)
Stan początkowy: czyste ciecze A i B
Stan końcowy: roztwór (AB) dwóch cieczy o nieograniczonej
rozpuszczalności wzajemnej. Ułamki molowe obu składników spełniają
nierówności: 0 x
A
1 oraz 0 x
B
1
A
(ciecz)
+ B
(ciecz)
roztwór (AB)
Warunki równowagi dla T = const.
i p=const.
gaz
A
roztwór
A
)
(
)
(
gaz
B
roztwór
B
)
(
)
(
Termodynamiczne funkcje mieszania
Entalpia mieszania:
Entropia mieszania:
Entalpia swobodna mieszania:
i
i
m
i
roztw
miesz
)
H
(
n
H
H
i
i
m
i
roztw
miesz
)
S
(
n
S
S
i
i
m
i
roztw
miesz
)
G
(
n
G
G
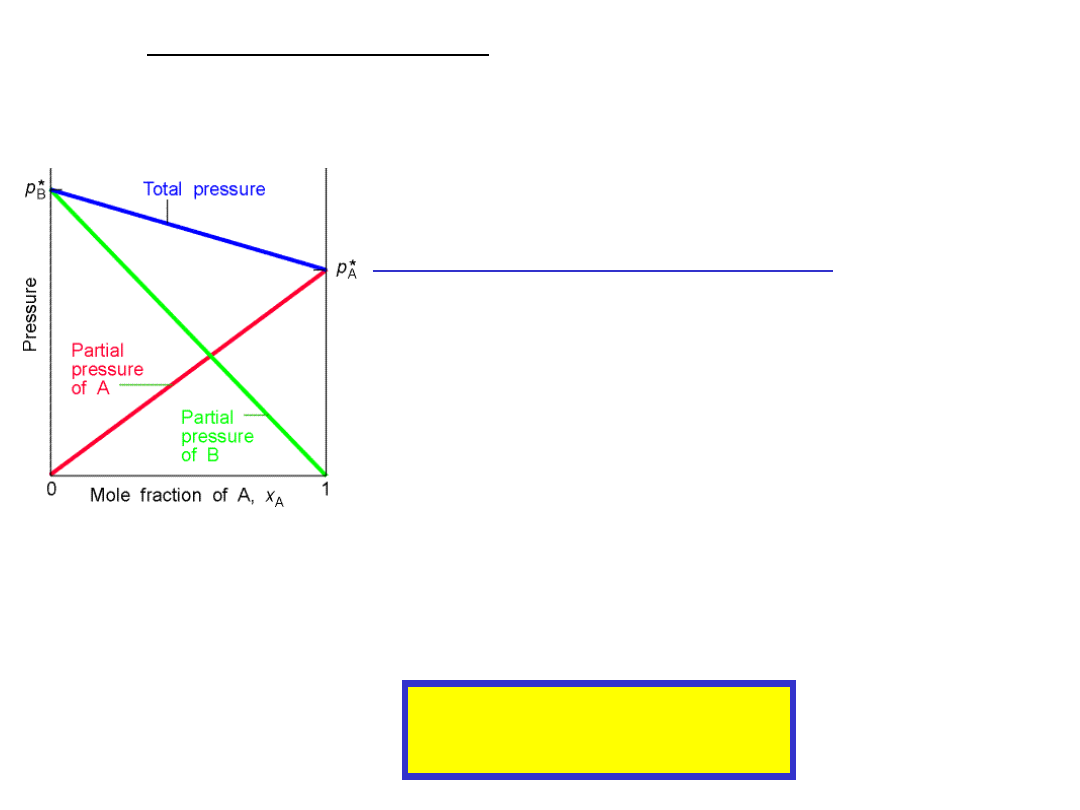
Roztwory doskonałe
x
p
p
i
o
i
i
Prężności składników roztworu zgodne z prawem Raoulta
Potencjał chemiczny składnika w roztworze:
RTlnx
)
(μ
μ
i
c
o
i
i
Entalpia swobodna mieszania:
i
i
m
i
roztw
mix
)
G
(
n
G
G
i
i
i
rozt
G
n
G
i
i
G
)
(
)
G
(
o
i
i
m
i
c
o
i
i
i
i
i
mix
)
(
n
n
G
Ponieważ
x
ln
RT
)
(
i
c
o
i
i
to
i
i
i
mix
x
ln
RT
n
G
gdzie G
i
-entalpia swobodna składnika w
roztworze Ξ potencjał chemiczny składnika
roztworu
gdzie (G
m
)
i
–molowa entalpia swobodna czystego składnika Ξ
standardowy potencjał chemiczny składnika
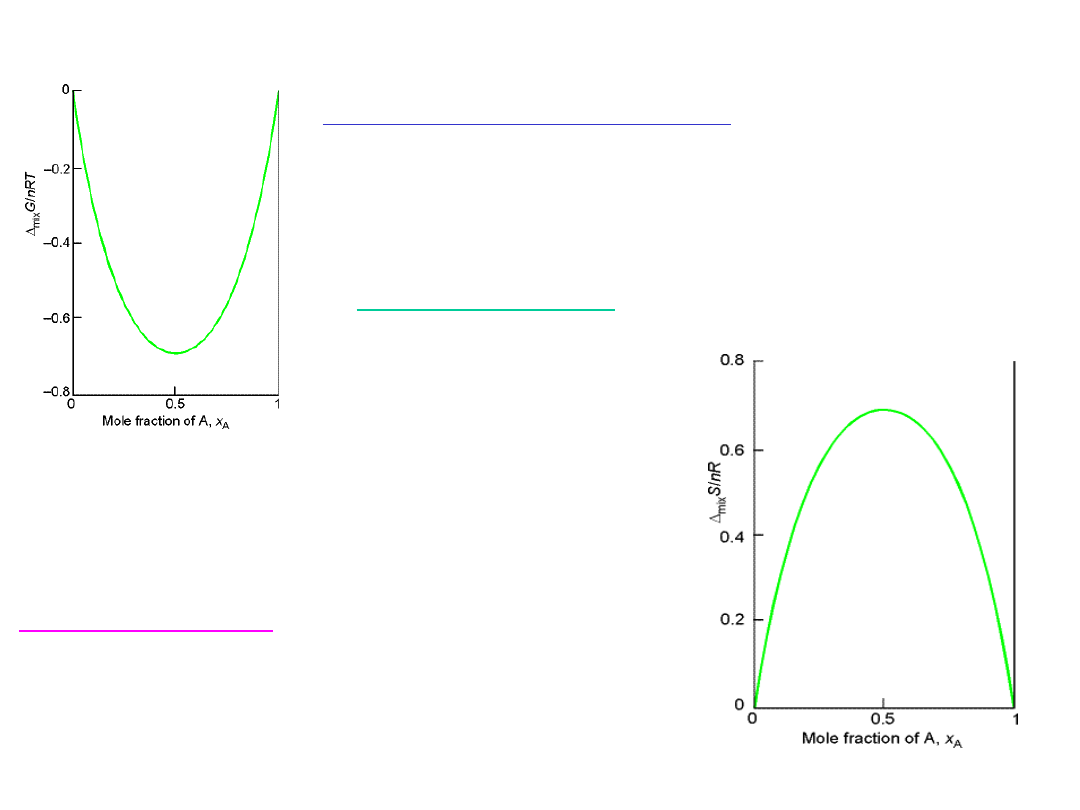
Termodynamiczne funkcje mieszania roztworów
doskonałych
Entalpia swobodna mieszania dla roztworu
doskonałego przyjmuje wartości ujemne, gdyż
entalpia swobodna roztworu jest mniejsza od
sumy entalpii swobodnych składników
i
i
m
i
roztw
)
G
(
n
G
Entropia mieszania
dla roztworu
doskonałego jest taka, jak dla gazów
spełniających równanie stanu gazu
doskonałego:
i
i
i
mix
x
ln
R
n
S
Entropia roztworu jest większa od sumy
entropii wszystkich składników.
W samorzutnym procesie mieszania
entropia wzrasta.
Entalpia mieszania
0
i
i
m
i
roztw
mix
)
H
(
n
H
H
Objętość mieszania:
0
i
i
m
i
roztw
mix
)
V
(
n
V
V
0
mix
mix
mix
S
T
G
H
Cząstkowe wielkości
molowe
Cząstkowa entalpia molowa składnika w roztworze:
Właściwości składnika w roztworze rzeczywistym, czyli w polu
oddziaływań innego rodzaju cząsteczek charakteryzują cząstkowe
wielkości molowe: cząstkowa molowa entalpia, cząstkowa molowa
objętość, cząstkowa molowa entalpia swobodna, zdefiniowane
następująco:
B
n
,
p
,
T
A
A
n
Y
Y
B
n
,
p
,
T
A
roztw
A
n
H
H
Cząstkowa molowa entalpia swobodna składnika w roztworze:
A
n
,
p
,
T
A
roztw
A
B
n
G
G
Cząstkowa molowa entalpia swobodna
jest równa potencjałowi chemicznemu składnika
Cząstkowa objętość molowa składnika w roztworze
B
n
,
p
,
T
A
roztw
A
n
V
V
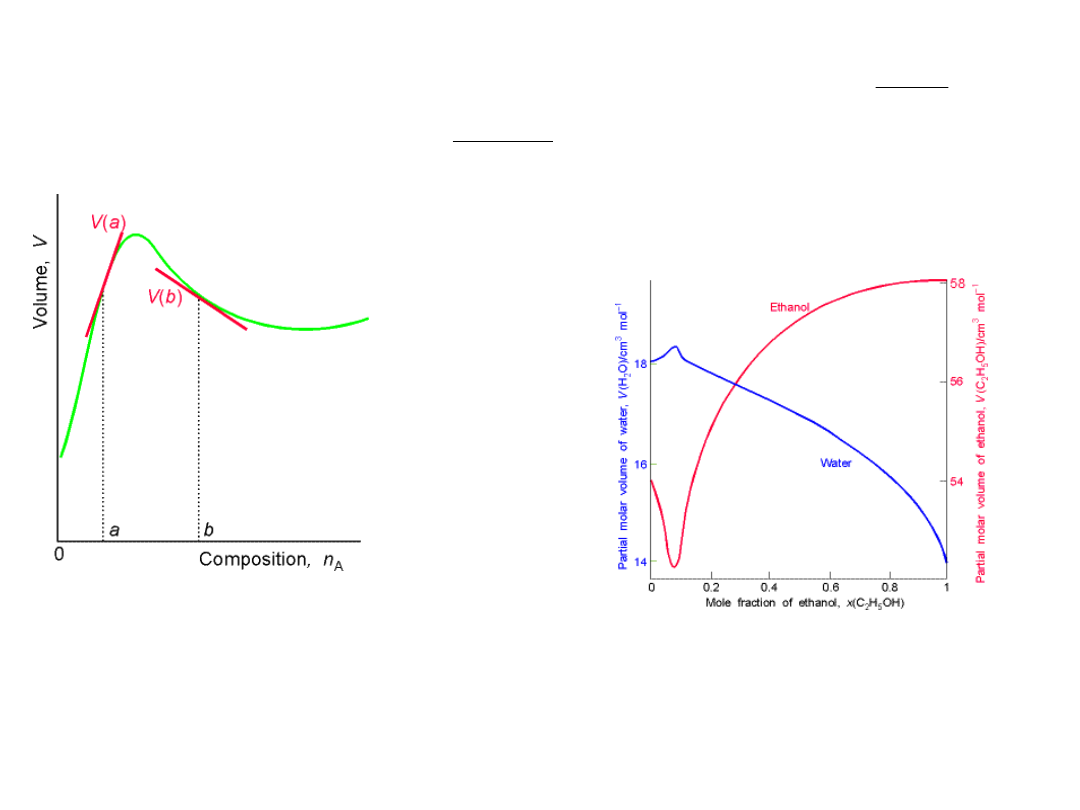
Cząstkowa objętość molowa składnika w
roztworze rzeczywistym (niedoskonałym)
B
n
,
p
,
T
A
roztw
A
n
V
V
Objętość roztworu rzeczywistego nie jest wielkością addytywną:
B
m
B
A
m
A
rozt
)
V
(
n
)
V
(
n
V
Objętość, jaką zajmuje 1 mol
składnika A w roztworze V
A
,
przyjmuje różne wartości,
zależne od składu roztworu i
różni się od objętości molowej
czystego składnika A, (V
m
)
A
.
Cząstkowe objętości molowe wody i
etanolu w roztworze:
w obecności etanolu, gdy x
EtOH
<0.2
woda w roztworze ma objętość większą
od czystej wody, natomiast gdy
x
EtOH
>0.2 ma objętość mniejszą.
Objętość ciekłego układu
dwuskładnikowego
B
B
A
A
B
n
T,
p,
B
A
n
T,
p,
A
dn
V
dn
V
dn
n
V
dn
n
V
dV
A
B
V = n
A
V
A
+ n
B
V
b
Cząstkowe objętości molowe V
i
znajduje się wyznaczając doświadczalnie zależność
całkowitej objętości układu V od składu.
V = f(n
i
)
Do wyników eksperymentalnych dopasowuje się funkcję opisującą zależność V = f
(n
A
)
np. V = a + bn
A
+ c(n
A
2
–1)
A
T,n
p,
A
A
2cn
b
n
V
V
)
B
2
A
B
A
A
B
n
1)c
(n
a
n
V
n
V
V
Objętości molowe substancji są zawsze dodatnie.
Cząstkowe objętości molowe nie muszą być > 0
np. graniczna cząstkowa objętość molowa MgSO
4
w wodzie wynosi – 1,4 cm
3
/
mol,
oznacza to, że dodatek 1 mola MgSO
4
do dużej objętości H
2
O spowoduje
zmniejszenie objętości o 1,4 cm
3
.
Hydratacja jonów soli przez cząsteczki wody powoduje kontrakcję
(zmniejszenie) objętości układu
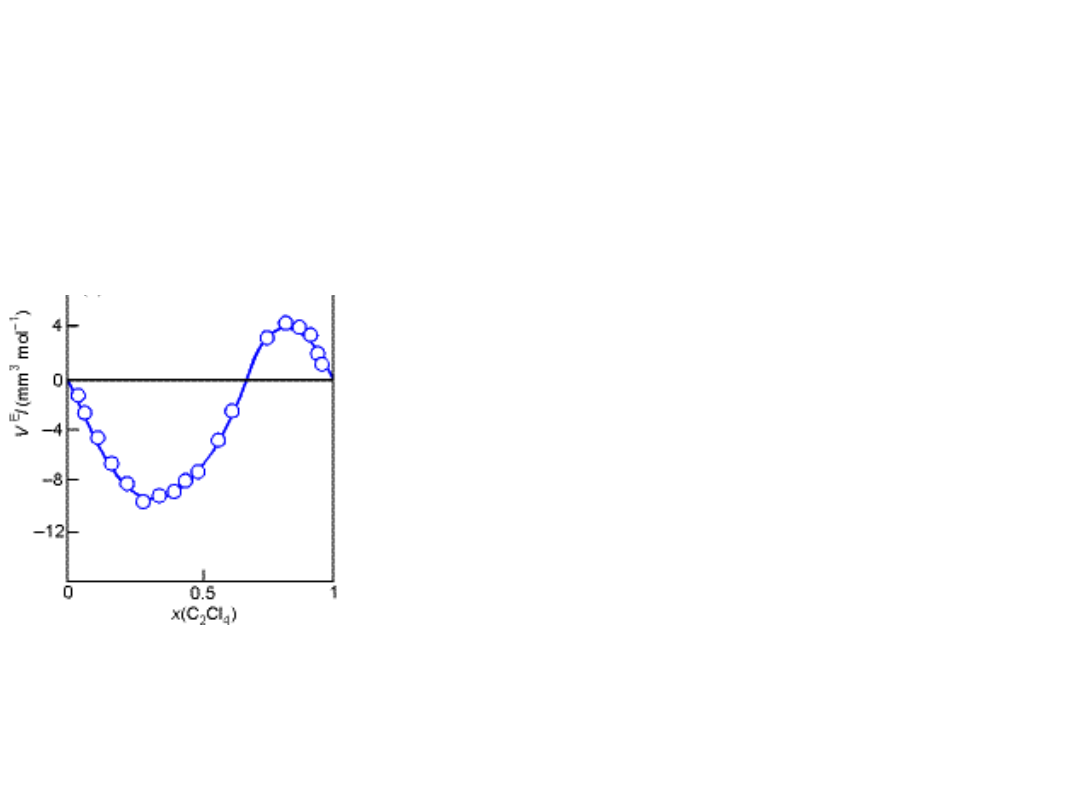
nadmiarowa objętość
mieszania
różnica pomiędzy objętością roztworu rzeczywistego i
roztworu doskonałego
id
roz
rz
roz
E
V
V
V
]
)
V
(
n
)
V
(
n
[
)
V
n
V
n
(
V
B
m
B
A
m
A
B
B
A
A
E
:
Nadmiarowa objętość mieszania jest
ujemna, czyli objętość roztworu jest
mniejsza niż suma objętości składników
kontrakcja objętości.
Nadmiarowa objętość mieszania jest
dodatnia
objętość roztworu jest większa
od sumy objętości składników.
nadmiarowa objętość mieszania:
Termodynamika roztworów
rzeczywistych
Jeżeli po zmieszaniu dwóch cieczy: A ( x
A
) i B (x
B
) otrzymany układ tworzy
roztwór idealny
, to
potencjał chemiczny każdego składnika roztworu wynosi
:
i
id
=
i
0
+ RT lnx
i
,
a termodynamiczne funkcje mieszania wynoszą:
∆
mix
G
id
= RT ( x
A
ln x
A
+ x
B
ln x
B
)
∆
mix
S
id
= - R ( x
A
ln x
A
+ x
B
ln x
B
)
H = G + T S
∆
mix
H
id
= 0
W przypadku
roztworów rzeczywistych:
potencjał chemiczny składnika roztworu wynosi
:
i
rz
=
i
0
+ RT lna
i
i
rz
=
i
0
+ RT lna
i
=
i
0
+ RT lnx
i
+RT ln
i
=
i
id
+ RT ln
i
,
∆
mix
G
rz
= RT ( x
A
ln a
A
+ x
B
ln a
B
)
dT
dlna
x
dT
dlna
x
RT
lna
x
lna
x
R
S
Δ
B
B
A
A
B
B
A
A
rz
mix
a
i
= f (T)
p
T
G
S
∆
mix
H
rz
=
mix
G
rz
+ T
mix
S
rz
=
dT
dlna
x
dT
dlna
x
RT
B
B
A
A
2
Nadmiarowe funkcje
mieszania
∆G
E
= ∆G
rz
- ∆G
id
= RT ( x
A
lnx
A
+x
A
ln
A
+ x
B
lnx
B
+x
B
ln
B
) – RT ( x
A
lnx
A
+x
B
lnx
B
) =
= RT ( x
A
ln
A
+x
B
ln
B
)
Dla układu doskonałego
A
=
B
=1 więc G
E
=0
Różnicę wartości funkcji termodynamicznej dla układu (roztworu) rzeczywistego X
rz
i
idealnego X
id
nazywamy
nadmiarem funkcji termodynamicznej
i oznaczamy X
E
X
E
=
X
rz
– X
id
nadmiarowa entalpia swobodna
id
mix
rz
mix
E
mix
)
G
(
)
G
(
G
nadmiarowa entropia mieszania
id
mix
rz
mix
E
mix
)
S
(
)
S
(
S
∆S
E
= ∆S
rz
- ∆S
id
=
dT
dlna
x
dT
dlna
x
RT
lna
x
lna
x
R
B
B
A
A
B
B
A
A
+ R ( x
A
ln x
A
+ x
B
ln x
B
)=
dT
dlnγ
x
dT
dlnγ
x
RT
lnγ
x
lnγ
x
R
B
B
A
A
B
B
A
A
Dla układu doskonałego ∆S
E
= 0 ponieważ
i
=1
nadmiarowa entalpia mieszania:
id
mix
rz
mix
E
mix
)
H
(
)
H
(
H
dT
dlnγ
x
dT
dlnγ
x
RT
dT
)
γ
dln(x
x
dT
)
γ
dln(x
x
RT
0
dT
dlna
x
dT
dlna
x
RT
ΔH
B
B
A
A
2
B
B
B
A
A
A
2
B
B
A
A
2
E
Dla układu doskonałego ∆H
E
= 0 ponieważ
i
=1
Klasyfikacja roztworów
Odchylenia funkcji nadmiarowych od zera wskazują na zakres odstępstw
roztworu rzeczywistego od roztworu idealnego
Podział roztworów:
Roztwory doskonałe
: ∆H
E
= 0, ∆S
E
= 0, ∆G
E
= 0
Roztwory rzeczywiste
: ∆H
E
0, ∆S
E
0, ∆G
E
0
roztwory elektrolitów, soli stopionych, roztwory o
oddziaływaniach
specyficznych
( wiązania wodorowe)
Roztwory atermalne
: ∆H
E
= 0, ∆S
E
0, ∆G
E
0
roztwory substancji o cząsteczkach podobnych pod
względem
chemicznym (np. węglowodory alifatyczne) ale znacznie
różniących się objętościami
molowymi.
Roztwory regularne (prawidłowe):
∆H
E
0 , ∆G
E
0 ,
∆S
E
= 0
cząsteczki obu składników są rozproszone w
sposób
przypadkowy (jak w roztworze idealnym) lecz
występują między nimi
oddziaływania o różnych energiach.
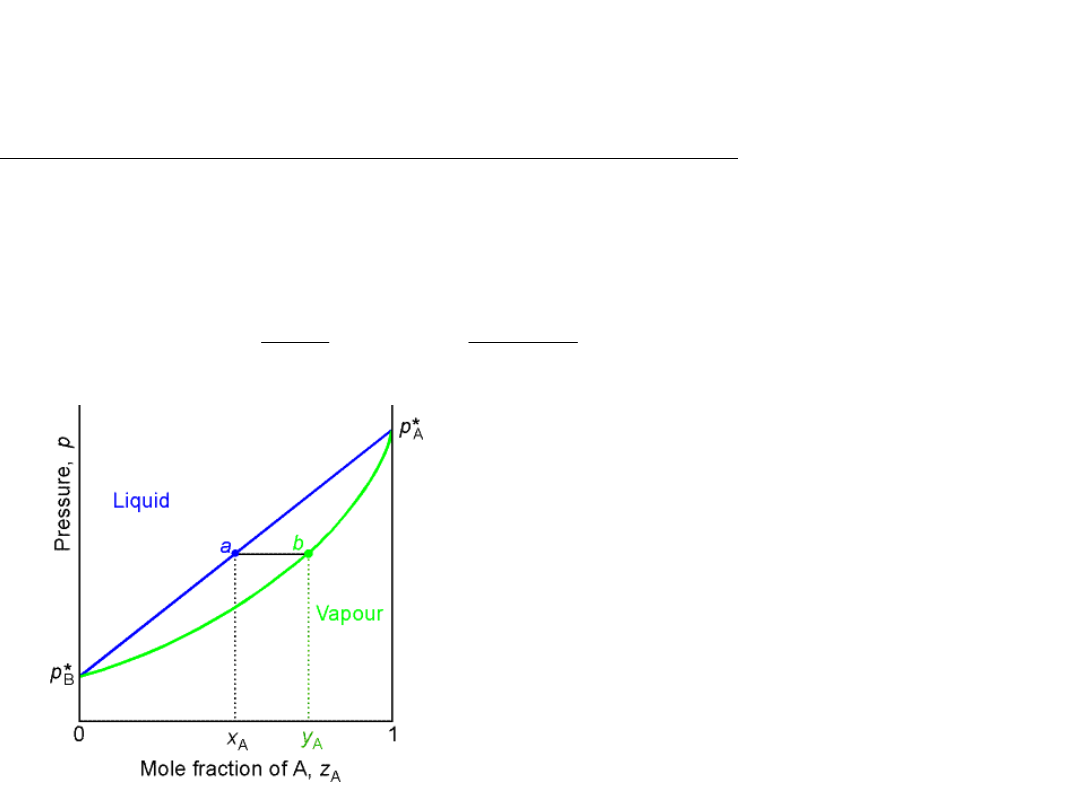
Równowaga ciecz-gaz w układach o nieograniczonej
rozpuszczalności obu składników w fazie ciekłej.
Zależność ciśnienia pary nasyconej od składu roztworu T=const.
B
o
B
A
o
A
B
A
x
p
x
p
p
p
p
Skład fazy gazowej określa ułamek molowy składnika w fazie gazowej : y
A
B
o
B
A
o
A
A
o
A
A
B
A
A
A
x
p
x
p
x
p
y
p
p
p
y
Cieczy, (w punkcie a) o składzie określonym
ułamkiem molowym x
A
odpowiada para, (w
punkcie b) o składzie określonym ułamkiem
molowym y
A.
Powyżej
prostej łączącej punkty p
A
oraz p
B
- jednofazowy układ ciekły,
poniżej
krzywej z punktami p
A
, b oraz p
B
para -jednofazowy układ gazowy.
Pomiędzy
prostą
i
krzywą
– dwie fazy w
równowadze: ciecz i para.
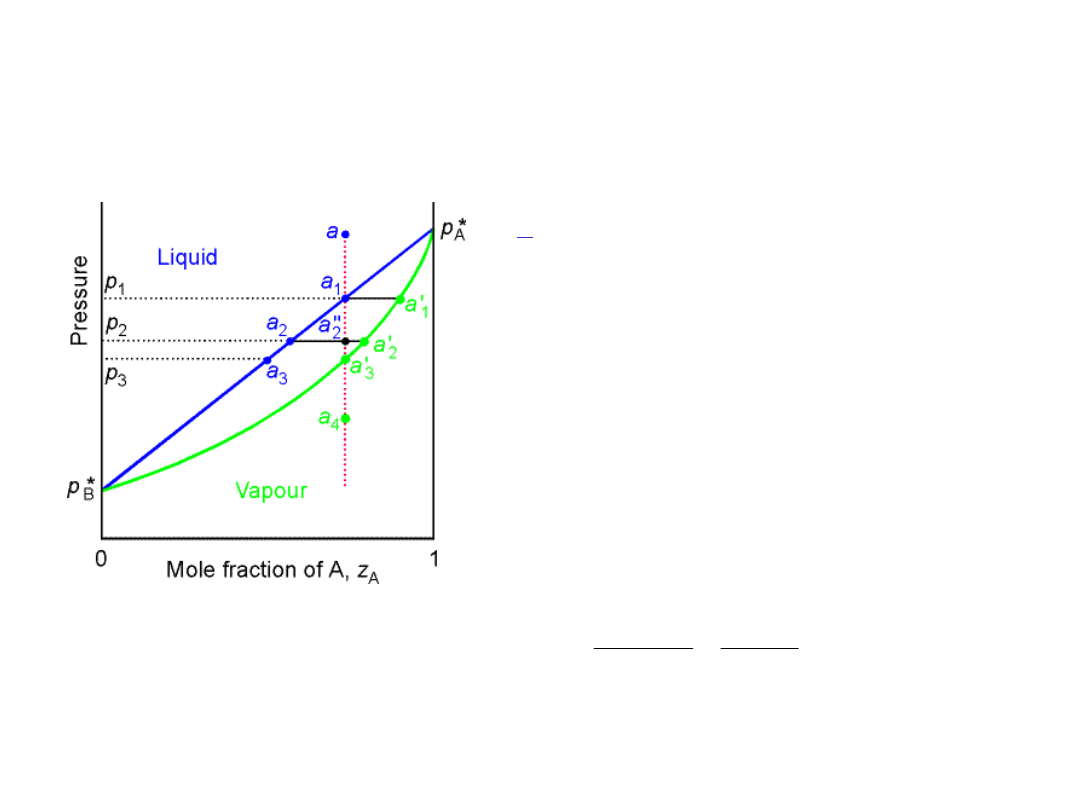
Wpływ ciśnienia na równowagę
ciecz-para
Linia przechodząca przez punkt
a
jest linią stałego składu.
Jeżeli p>p
1
układ jednofazowy ciekły,
ciecz a
1
Jeżeli p< p
3
układ jednofazowy gazowy
- para nienasycona a
3
’
.
Jeżeli p
3
<p<p
1
czyli p=p
2
dwie fazy:
ciecz a
2
i para nasycona a
2
’
.
Stosunek liczby moli składnika A w obu
fazach można obliczyć stosując regułę
dźwigni:
2
2
2
2
a
a
a
a
)
n
(
)
n
(
''
'
'
'
gaz
A
ciecz
A
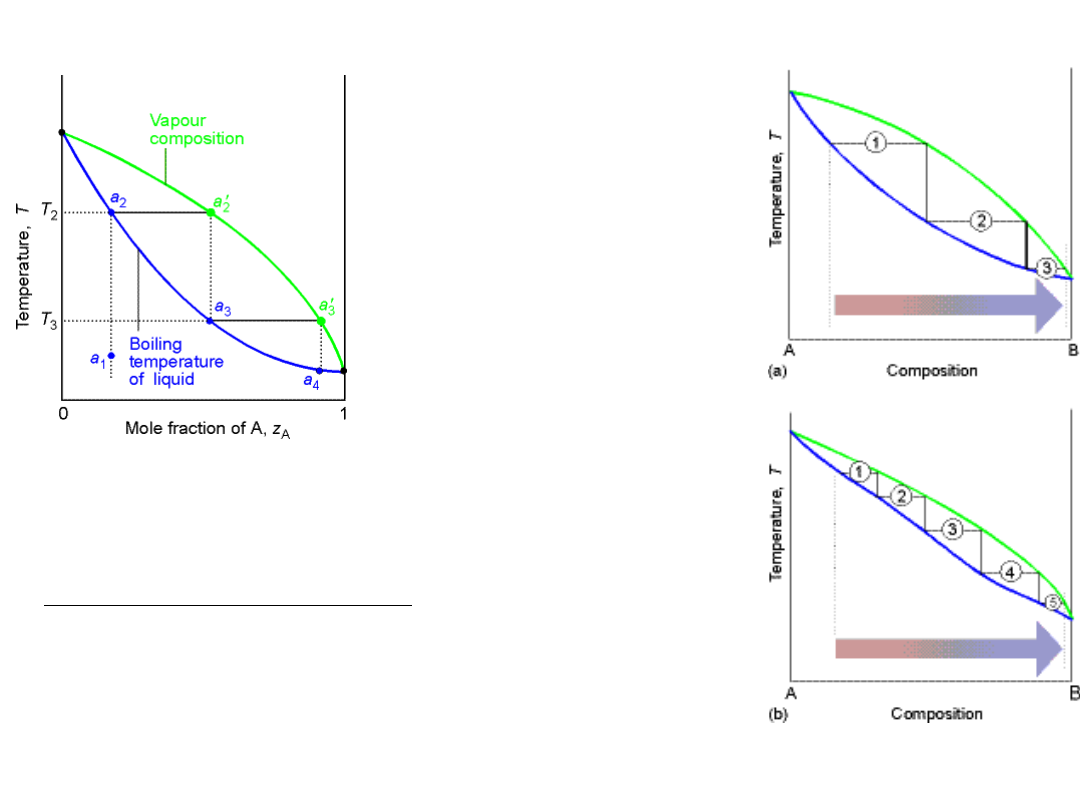
Wpływ temperatury na równowagę ciecz –
para dla p = const.
Składnik A jest bardziej
lotny (wyższa prężność stąd
niższa temperatura wrzenia
pod normalnym ciśnieniem).
Ciecz o składzie a
1
ogrzana do temperatury
T
2
wrze para o składzie
a
2
’
, po skropleniu
kondensat o składzie a
3
,
który ogrzany do
temperatury T
3
wrze,
dając parę nasyconą o
składzie a
3
’
.
W destylacji frakcyjnej (rektyfikacji) procesy
wrzenia i kondensacji powtarzane są wielokrotnie,
na kolejnych półkach kolumny rektyfikacyjnej.
Liczba półek teoretycznych - liczba efektywnych
procesów wrzenia i kondensacji, która jest
niezbędna do otrzymania z mieszaniny wyjściowej
destylatu o założonym składzie.
Liczba półek teoretycznych jest cechą charakterystyczną roztworu.
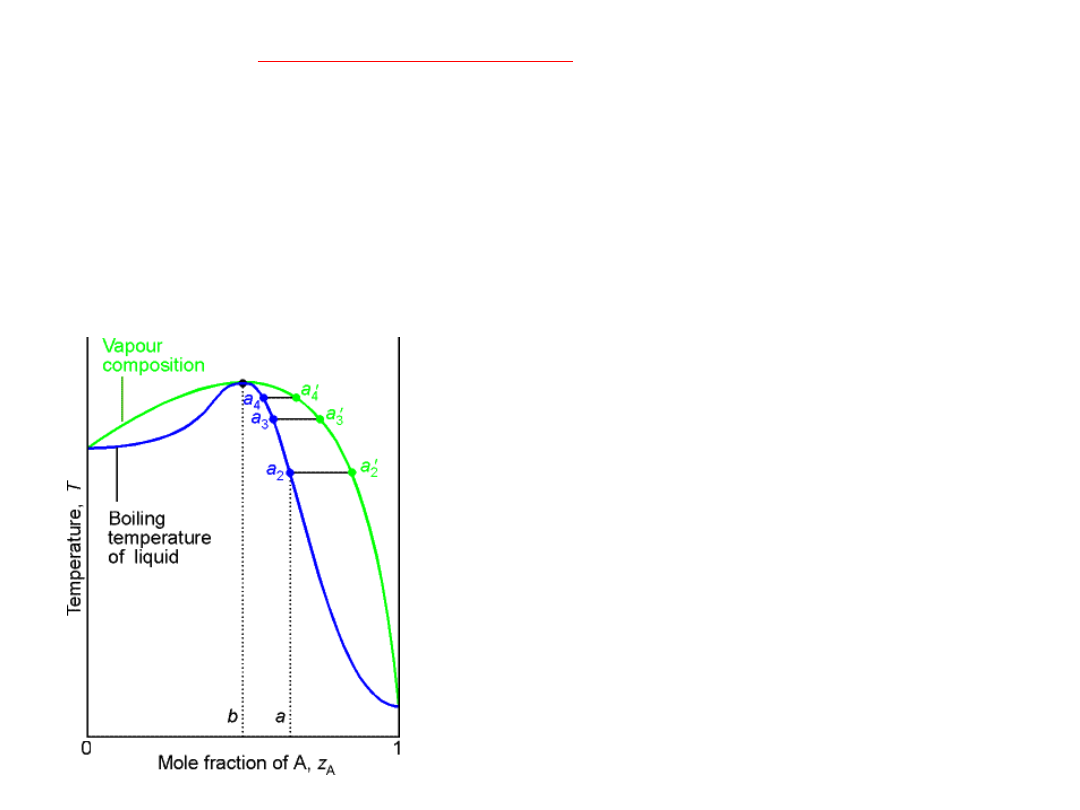
AZEOTROPY ujemne
Prężności składników mogą wykazywać znaczne odchylenia od liniowej
zależności przewidzianej prawem Raoulta.
Jeżeli prężności obu składników roztworu są mniejsze niż przewiduje
prawo Raoulta
B
o
B
B
A
o
A
A
x
p
p
oraz
x
p
p
zależność p
rozt
=f( x
A
) dla T=const. wykazuje minimum
, natomiast
zależność T
wrz
=f(x
A
) dla p=const. (przedstawiona na rysunku) wykazuje
maksimum
azeotrop ujemny
.
W punkcie azeotropowym (b) skład pary
jest identyczny ze składem cieczy -
wrzenie roztworu nie powoduje zmiany
składu mieszaniny azeotropowej nie
można rozdzielić metodą destylacji
frakcyjnej.
Azeotropy ujemne: H
2
O+HNO
3
, H
2
O+HCl
Prężność składnika, mniejsza od wartości
oczekiwanej, wskazuje na silne przyciąganie
pomiędzy cząsteczkami obu składników
oddziaływania różnoimienne są silniejsze od
oddziaływań jednoimiennych.
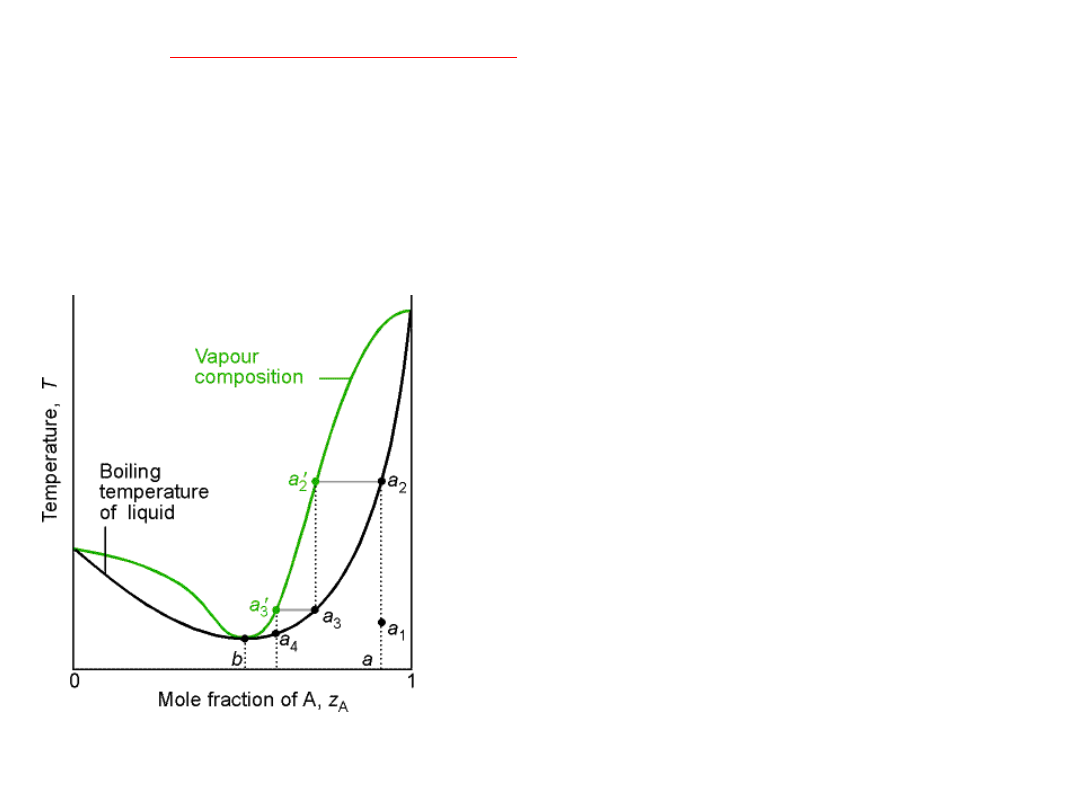
AZEOTROPY dodatnie
Jeżeli prężności obu składników roztworu są większe niż przewiduje prawo Raoulta
B
o
B
B
A
o
A
A
x
p
p
oraz
x
p
p
zależność p
rozt
=f(x
A
) dla T=const. wykazuje maksimum
, natomiast
zależność T
wrz
=f(x
A
) dla p=const. (przedstawiona na rysunku) wykazuje
minimum
azeotrop dodatni
.
Przykłady azeotropów dodatnich:
benzen-metanol,
etanol- woda (skład azeotropowy -
96% molowych EtOH, t
wrz
= 78,1
0
C,
azeotropu nie można rozdzielić
przez destylację frakcyjną.
Prężność składnika, większa od
wartości oczekiwanej, wskazuje na
odpychanie cząsteczek obu
składników
oddziaływania
jednoimiennych są silniejsze od
oddziaływań.
Document Outline