Laboratorium Teorii Regulacji II WSTĘP DO MATLAB
Cel ćwiczenia: wprowadzenie do modelowania w matlabie.
1. Modelowanie transmitancji operatorowej
Transmitancja operatorowa - transfer function Transmitancję operatorową obiektu modelujemy za pomocą następującego polecenia
:
a=tf([1 -2] , [2 1 3])
wykonanie tego polecenia spowoduje przyporządkowanie do zmiennej a transmitancji operatorowej następującej postaci s − 2
G( s) =
2 2
s + s + 3
2. Opis układu w postaci przestrzeni stanu. (state space).
Należy w pierwszej kolejności podać wszystkie macierze opisujące stan obiektu A,B,C, D, dla układów jednowymiarowych macierze te przyjmą następującą postać: (n liczba równań różniczkowych zwyczajnych I- rzędu.) A- macierz stanu o wymiarze nxn.
B- macierz sterowań wymiarze nx1 (macierz wejść).
C- macierz wyjść o wymiarze 1xn .
D- macierz transmisyja o wymiarze 1x1 (macierz bezpośredniego oddziaływania wejścia na wyjście.
Dla przedstawionego powyżej przykładu macierze będą odpowiednio następującej postaci
A=[0 1; -0.5 -0.5]
B=[0;1]
C=[-2 1]
D=[0]
Wydając polecenie ms=ss(A,B,C,D) przypisujemy postać przestrzeni stanu do zmiennej ms.
3. Opis modeli dyskretnych odbywa się analogicznie do modeli ciągłych z tą różnicą, że musimy jeszcze do opisu dodać czas próbkowania.
Przykładowo obiekt
18
,
0
F ( ) =
z
z
modelujemy w za pomocą następującego
2
z + − 6
,
1 z + 7
,
0
polecenia
disc=tf([0.18 0] , [1 -1.6 0.7], .01)
4. Modelowanie opóźnień w układach ciągłych i dyskretnych.
Można zamodelować dwa rodzaje opóźnień wejściowe (inputdelay) i wyjściowe (outputdelay) i to zarówno dla systemów ciągłych jak i dyskretnych.tak jak w zamieszczonych przykładach poniżej.
Del_disc=tf(0.18, [1 -1.6 0.7], .01 , ‘outputdelay’,7)
Dla układów dyskretnych czas opóźnienienia ( w naszym przypadku 7) musi być dodatni i musi być krotnością czasu próbkowania.
Dla układów ciągłych
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) 5. Lista dodatkowych funkcji Control Toolbox System.
size(nazwa_modelu) – podaje liczbę wyjść i wejść dla sprawdzanego modelu przykład:
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) size(tr)
ndims(nazwa modelu) podaje ilość wymiarów modelu.
przykład:
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) ndims(tr)
isct(nazwa_modelu) - zwraca 1 gdy model jest modelem ciągłym.
przykład:
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) isct(tr)
isdt(nazwa_modelu) – zwraca 1, gdy model jest dyskretny.
przykład:
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) isdt(tr)
hasdelay(nazwa_modelu) – zwraca 1 w przypadku gdy w układzie występują opóźnienia.
przykład:
tr=tf(0.18, [1 -1.6 0.7] , 'inputdelay',7) hasdelay(tr)
6. Tworzenie schematów połączeń pomiędzy modelami.
Połączenie równoległe:
S1+S2 = parallel(S1,S2)
Przykład:
S1=tf(1,[1 2 1]);
S2=tf(2,[2 2 2]);
parallel(S1,S2)
połączenie szeregowe
S1*S2 = series(S1,S2)
Przykład:
S1=tf(1,[1 2 1]);
S2=tf(2,[2 2 2]);
series(S1,S2)
sprzężenie zwrotne
gs=feedback(S1,S2)
gdzie S1- element w torze głównym, S2 - transmitacja toru powrotnego.
Przykład:
S1=tf(1,[1 2 1]);
S2=tf(2,[2 2 2]);
gs= feedback(S1,S2)
7. Polecenia konwersji.
sys1=c2d(model_ciągły, Ts) - polecenie dyskretyzacji Ts – czas próbkowania/
tc=tf(1 , [1 1 1])
td=c2d(tc , 0.01)
sys1=d2c(model_dyskretny) - polecenie przekształca model dyskretny w ciągły td=tf(1 , [1 1 1] , .01)
tc=d2c(td)
sys1=d2d(model_dyskretny, Ts) – polecenie zmieniające okres próbkowania na Ts td=tf(1 , [1 1 1] , .01)
tc=d2d(td , 0.1)
8. Najważniejsze charakterystyki.
bode(model) – chrakterystyka logarytmiczna amplitudowa i fazowa step(model) – odpowiedź skokowa
nyquist(model) – charakterystyka amplitudowo-fazowa impulse(model) – odpowiedź impulsowa
Istnieje możliwość wykreślenia na jednym wykresie np. odpowiedzi skokowych 2
obiektów i ich porównanie. Możemy dokonać tego wydając komendę „hold on”
następnie wykreślić dowolną liczbę charakterystyk wykorzystując polecenie hold i dokonać ich porównania. Komendę likwidujemy poleceniem „hold off”.
Możliwe jest także skorzystania z następującego wywołania komendy np.
step(model1, model2, model3) spowoduje to wykreślenie na jednym wykresie trzech charakterystyk.
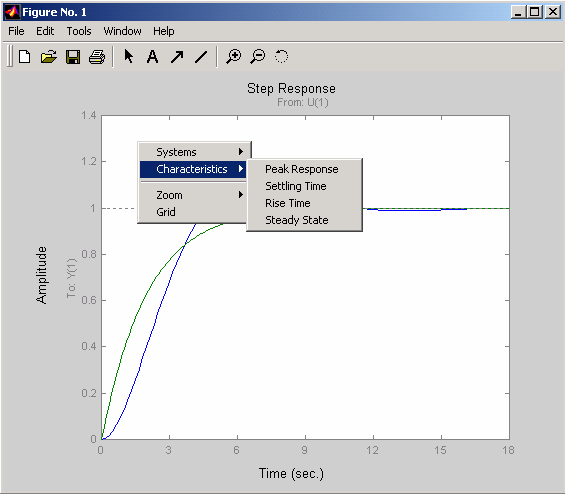
Następnie klikając prawym klawiszem myszy w obszar wykresu możemy uzyskać dodatkowe informacje o charakterystyce. (patrz rys 1) Rys1. Menu kontekstowe.
9. Ćwiczenia do wykonania
• Zapoznaj się z poszczególnymi komendami pakietu Control System Toolbox.
• Zamodeluj transmitancje operatorowe obiektów podanych przez prowadzącego.
• Zapoznaj się z funkcjami konwersji patrz pkt7.
• Dla zadanego modelu (obiektu) wykreśl wszystkie podane powyżej charakterystyki.
• Jakie informacje można odczytać z menu kontekstowego wykresu (podaj wszystkie możliwe parametry dla każdej z charakterystyk).
• Korzystając z poleceń parallel, series, feedback zamodeluj podany przez prowadzącego schemat blokowy.
• Wpisując w linii komend polecenie simulink zapoznaj się z możliwościami pakietu simulink.