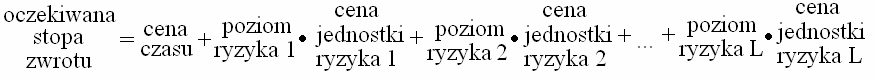III MODELE INWESTYCYJNE

___________________________________________________________________________

MODELE WIELOCZYNNIKOWE, MODEL APT

1. Wstęp

Modele wieloczynnikowe powstały jako rozwinięcie modelu Sharpe’a. Zauważono bowiem, że stopa zwrotu z akcji zależy nie tylko od wahań indeksu rynkowego, ale także sytuacji w branży, poziomu inflacji, etc. Aby uwzględnić ten fakt w modelu jako dodatkowe czynniki objaśniające wprowadzono zmienne inne niż stopa zwrotu z indeksu rynkowego.

Modele przedstawione dotychczas opisywały zachowanie stóp zwrotu. Nie mówią one jednak, jak kształtować się będą ceny i stopy zwrotu w stanie równowagi. W tym celu stworzono modele wyceny aktywów kapitałowych. Opisują one zachowanie stóp zwrotu w sytuacji gdy na rynku kapitałowym panuje równowaga, a racjonalni inwestorzy poszukują portfeli optymalnych ze względu na stosunek ryzyka i stopy zwrotu.

Najbardziej ogólnym modelem równowagi jest model APT ( Arbitrage Pricing The-ory) zaprezentowany przez Stephena Rossa w 1976 r.

2. Modele wieloczynnikowe

założenia

Modele wieloczynnikowe skonstruowano w oparciu o dwa podstawowe założenia: a) źródłem powodującym występowanie zależności między stopami zwrotu z akcji różnych spółek są wyłącznie zmiany pewnej grupy indeksów,

b) relacja pomiędzy zmianami stopy zwrotu z danej akcji a zmianami stopy zwrotu z poszczególnych indeksów jest liniowa.

podstawowe równanie modelu

R = a + b I + b I + ... + b I + ξ

i

i

i 1 1

i 2 2

iL L

i

gdzie:

Ri – stopa zwrotu z i-tej akcji (i = 1, 2, ..., N)

I1, I2, ..., IL – wartość pierwszego, drugiego, ..., L-tego indeksu

ai, bi1, bi2, ..., biL – parametry modelu

ξi – składnik losowy (zaburzenie losowe)

Oznaczenia:

Ri - wartość oczekiwana stopy zwrotu z i-tej akcji

2

σ i - wariancja stopy zwrotu z i-tej akcji

2

σ ei - wariancja składnika losowego i-tej akcji

- 1 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

I , I ,..., I

1

2

L - wartość oczekiwana pierwszego, drugiego, ..., L-tego indeksu 2

2

2

σ ,σ ,...,σ

I

- wariancja pierwszego, drugiego, ..., L-tego indeksu

1

I 2

IL

własności modelu

E(ξ i ) = 0

składnik losowy ma wartość przeciętną równą 0

(

cov ξ , I

i

j ) = 0

składnik losowy jest nieskorelowany z indeksami – reprezentuje

j=1,2,...,L

on wpływ zdarzeń dotyczących wyłącznie danej spółki

cov(ξ ,ξ

i

j ) = 0

składniki losowe różnych akcji są nieskorelowane – zależność

dla i ≠ j

między stopami zwrotu wynika wyłącznie ze zmian indeksów

cov( I , I

j

k ) = 0

indeksy są nieskorelowane – reprezentują wpływ różnych

dla j ≠ k

czynników

charakterystyki stóp zwrotu

R = a + b I + b I + ...+ b I

i

i

i 1 1

i 2 2

iL L

wartość oczekiwana stopy zwrotu z i-tej

akcji

2

2

2

2

2

2

2

2

σ = b σ + b σ + ... b σ + σ

i

i 1

I 1

i 2

I 2

iL

IL

ei wariancja stopy zwrotu z i-tej akcji

(

cov R , R

b b σ

b b σ

i

j ) =

2 +

2 +

i 1

j 1

I 1

i 2

j 2

I 2

kowariancja między stopami zwrotu z i-tej

2

+ ... + b b σ

iL

jL

IL

oraz j-tej akcji

(

cov R , R

i

j )

cor( R , R =

i

j )

σ σ

współczynnik korelacji między stopami

i

j

zwrotu z i-tej oraz j-tej akcji

interpretacja parametrów

bij jest miarą wrażliwości – mówi o ile punktów procentowych zmieni się stopa zwrotu z akcji, jeżeli wartość j-tego indeksu wzrośnie o jednostkę

ai wskazuje przeciętną stopę zwrotu jaką można osiągnąć z danej akcji, jeżeli wartości wszystkich indeksów wynoszą 0 jednostek

- 2 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

parametry portfela aktywów

Parametry portfela aktywów można uzyskać dysponując wartościami parametrów dla poszczególnych aktywów. W tym celu należy obliczyć średnią ważoną parametrów dla aktywów wchodzących w skład portfela; wagami są wartościowe udziały aktywów w ogólnej kapitalizacji portfela.

k

b =

1

∑ w b

i

i 1

i =1

k

b =

2

∑ w b

i

i 2

i =1

(...)

k

b =

w b

L

∑ i iL

i =1

k

a = ∑ w a

i

i

i =1

gdzie:

b1, b2, ..., bL, a – parametry portfela aktywów

k – ilość aktywów w portfelu

w1, w2, ..., wk – wartościowe udziały aktywów w portfelu

b11, b12, ..., b1L, a1 – parametry pierwszej akcji

b21, b22, ..., b2L, a2 – parametry drugiej akcji

(...)

bk1, bk2, ..., bkL, ak – parametry k-tej akcji

3. Model arbitrażu cenowego (APT)

założenia

1. Na rynku nie istnieje możliwość dokonywania arbitrażu, a modelem opisującym kształtowanie się stóp zwrotu jest liniowy model wieloczynnikowy.

2. Oczekiwania inwestorów odnośnie charakterystyk instrumentów finansowych (oczekiwanych stóp zwrotu, etc.) są jednorodne.

3. Aktywa są doskonale podzielne.

4. Nie ma kosztów transakcyjnych oraz podatków od zysków kapitałowych.

5. Pojedynczy inwestorzy nie mają wpływu na ceny aktywów.

6. Dozwolona jest nieograniczona krótka sprzedaż.

7. Istnieje nieograniczona możliwość udzielania oraz zaciągania kredytu po stopie wolnej od ryzyka.

8. Wszystkie aktywa mogą być bez przeszkód przedmiotem transakcji rynkowych.

9. Wszyscy inwestorzy podejmują decyzje na jeden okres.

- 3 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

podstawowe równanie modelu

R = R + b R

− R

+ b R

− R

+ ... + b R

− R

+ ξ

i

F

i 1 (

P 1

F )

i 2 (

P 2

F )

iL (

PL

F )

i

gdzie:

Ri – stopa zwrotu z i-tej akcji (i = 1, 2, ..., N)

RF – stopa procentowa wolna od ryzyka

RP1, RP2, ..., RPL – stopa zwrotu właściwa dla pierwszego, drugiego, ..., L-tego czynnika ryzyka

bi1, bi2, ..., biL – parametry modelu

ξi – składnik losowy (zaburzenie losowe)

Oznaczenia:

Ri - wartość oczekiwana stopy zwrotu z i-tej akcji

R , R

,..., R

P 1

P 2

PL - wartość oczekiwana stopy zwrotu właściwej dla pierwszego, drugiego, ..., L-tego czynnika ryzyka

własności modelu

E(ξ i ) = 0

składnik losowy ma wartość przeciętną równą 0

charakterystyki stóp zwrotu

R = R + b R

− R

+ b R

− R

+ ... + b R

− R

wartość oczekiwa-

i

F

i 1 (

P 1

F )

i 2 (

P 2

F )

iL (

PL

F )

na stopy zwrotu z i-tej akcji

interpretacja parametrów

R

R

b

R

− R

i

F

i 2 (

P 2

F )

W modelu APT na oczekiwaną stopę zwrotu wpływają:

a) cena czasu – stopa procentowa wolna od ryzyka,

b) poziom danego ryzyka – mierzony współczynnikiem b,

c) cena jednostki ryzyka – mierzona różnicą ( R − R .

P

F )

- 4 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

Z konstrukcji modelu wynika, że:

a) instrument pozbawiony ryzyka (wszystkie współczynniki b równe 0) cechuje się przeciętną stopą zwrotu wolną od ryzyka RF,

b) instrument o poziomie j-tego ryzyka równym 1, a wszystkich innych równych 0

cechuje się przeciętną stopą zwrotu równą R .

Pj

parametry portfela aktywów

Parametry portfela aktywów można uzyskać dysponując wartościami parametrów dla poszczególnych aktywów. W tym celu należy obliczyć średnią ważoną parametrów dla aktywów wchodzących w skład portfela; wagami są wartościowe udziały aktywów w ogólnej kapitalizacji portfela.

k

b =

1

∑ w b

i

i 1

i =1

k

b =

2

∑ w b

i

i 2

i =1

(...)

k

b =

w b

L

∑ i iL

i =1

gdzie:

b1, b2, ..., bL – parametry portfela aktywów

k – ilość aktywów w portfelu

w1, w2, ..., wk – wartościowe udziały aktywów w portfelu

b11, b12, ..., b1L – parametry pierwszej akcji

b21, b22, ..., b2L – parametry drugiej akcji

(...)

bk1, bk2, ..., bkL – parametry k-tej akcji

- 5 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

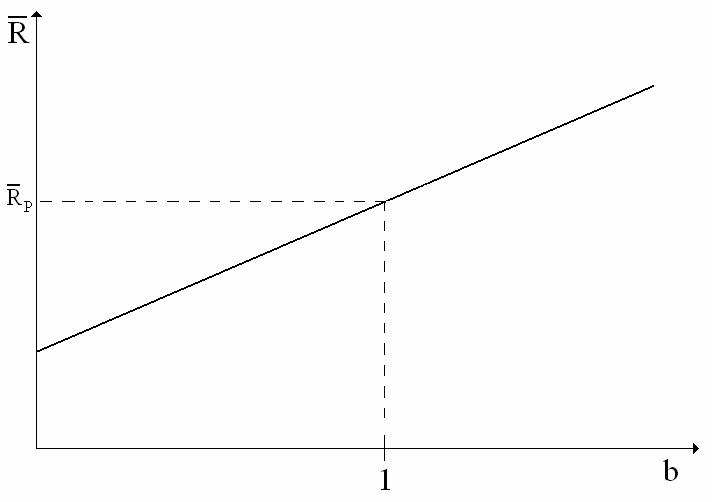
linie i płaszczyzny arbitrażu cenowego

Linia (płaszczyzna) arbitrażu cenowego ( Arbitrage Pricing Line) ukazuje zależność między wartościami współczynników b (przy stałych R , R

,..., R

) a oczekiwaną

P 1

P 2

PL

stopą zwrotu.

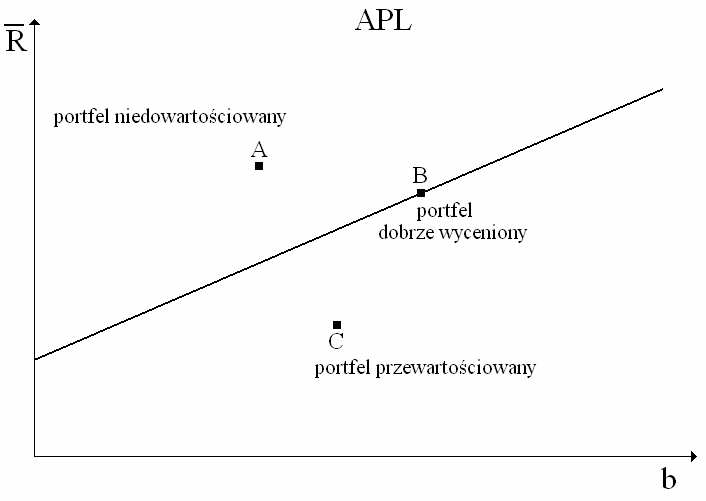
Portfel dobrze wyceniony – portfel którego oczekiwana stopa zwrotu jest równa ocze-kiwanej stopie zwrotu wynikającej z modelu APT (rekomendacja – trzymaj) Portfel niedowartościowany – portfel którego oczekiwana stopa zwrotu jest wyższa niż oczekiwana stopa zwrotu wynikająca z modelu APT (rekomendacja – kupuj) Portfel przewartościowany – portfel którego oczekiwana stopa zwrotu jest niższa niż

oczekiwana stopa zwrotu wynikająca z modelu APT (rekomendacja – sprzedaj)

- 6 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

MODELE WIELOCZYNNIKOWE, MODEL APT – ZADANIA

Zad.1.

Stopa zwrotu z akcji PKN Orlen może być opisana następującym modelem dwuczynniko-wym:

R =

06

,

0

+ 5

,

1 ⋅ I + 8

,

0 ⋅ I + ξ

1

2

gdzie I1 oznacza procentową zmianę ceny baryłki ropy, a I2 procentową zmianę indeksu WIG.

Wiedząc, że:

oczekiwany jest wzrost ceny ropy o 10%, a odchylenie standardowe procentowej zmiany ceny baryłki ropy wynosi 30%,

oczekiwany jest spadek indeksu WIG o 5%, a odchylenie standardowe stopy zwrotu z WIG-u wynosi 20%,

odchylenie standardowe składnika losowego wynosi 10%, oblicz:

a) oczekiwaną stopę zwrotu z akcji PKN Orlen,

b) odchylenie standardowe stopy zwrotu z akcji PKN Orlen.

Zad.2.

Oszacowano model APT o dwóch czynnikach ryzyka, do których zaliczono inflację oraz produkcję przemysłową. Premia za ryzyko wynikające ze zmian stopy inflacji wynosi 2%, a poziomu produkcji przemysłowej 5%. Wiedząc, że oczekiwana stopa zwrotu z akcji KGHM

wynosi 14%, współczynnik b właściwy inflacji 1,5, a współczynnik b właściwy produkcji przemysłowej 1,2, oszacuj poziom stopy wolnej od ryzyka.

Zad.3.

Oszacowano model APT o jednym czynniku ryzyka. Ma on postać:

R =

03

,

0

+ b ⋅ 04

,

0

Wiedząc jednocześnie, że akcje PZU cechują się współczynnikiem b równym 1,5 oraz oczekiwaną stopą zwrotu wynoszącą 10%:

a) określ poziom stopy wolnej od ryzyka,

b) określ ile wynosi premia za uwzględnione w modelu ryzyko,

c) narysuj linię APL i zaznacz położenie akcji PZU,

d) oceń czy akcje PZU są: dobrze wycenione, niedowartościowane, przewartościowane, e) jeśli to możliwe zaproponuj strategię arbitrażową.

Zad.4.

Wiedząc, że stopa zwrotu z akcji GM jest uzależniona od stopy zwrotu z indeksu S&P500

oraz procentowej zmiany poziomu produkcji przemysłowej w USA, oszacuj parametry modelu dwuczynnikowego.

Stopa zwrotu

Stopa zwrotu

Procentowa zmiana poziomu

Okres

z akcji GM

z S&P500

produkcji przemysłowej

Q1 2011

15,00%

5,00%

5,00%

Q2 2011

27,50%

15,00%

0,00%

Q3 2011

-7,50%

-5,00%

-10,00%

Q4 2011

-5,00%

-5,00%

-5,00%

Q1 2012

-5,00%

-10,00%

10,00%

- 7 -

 by Rafał Buła

III MODELE INWESTYCYJNE

___________________________________________________________________________

MODELE WIELOCZYNNIKOWE, MODEL APT – ZADANIA DO-

MOWE

Zad.5.

Załóżmy, że na stopę zwrotu z akcji dowolnej spółki mają wpływ dwa czynniki: 1. stopa zwrotu z indeksu rynkowego,

2. stopa zwrotu z indeksu branżowego, właściwego dla danej spółki.

Indeksy branżowe są nieskorelowane pomiędzy sobą, jak i z indeksem rynkowym. Dysponując danymi z tabeli, oblicz oczekiwaną stopę zwrotu z akcji Lotosu oraz ING oraz odchy-lenia standardowe stopy zwrotu.

Indeks

Indeks

Indeks

Spółka

Lotos

ING

rynkowy

paliwowy

bankowy

R

10%

20%

15%

i

ai

3%

2%

0%

0%

0%

bi1

0,7

0,9

1

0

0

bi2

1,5

0

0

1

0

bi3

0

1,2

0

0

1

σi

20%

30%

25%

σei

10%

15%

-

-

-

- 10 -

 by Rafał Buła