W4-1 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

Równoważność LRR i układu LRR

a x( n + m) + a

x( n

L

−

+ m − )

1 +

+ a x( n + )

1 + a x( n) = f ( n) m

m 1

1

0

warunki początkowe: x( m

)

1 ,L

−

, x )

1

( , x(0)

m

m 1

M ( z) = a z + a

z −

L

−

+ + a z + a

m

m 1

1

0

f ( n) ≡ ,

0

am = 1

x( n + m) + a

x(

L

m−

n + m − )

1 +

+ a x( n + )

1 + a x( n) = 0

1

1

0

m

m 1

M ( z) = z + a

z −

L

−

+ + a z + a

m 1

1

0

x ( n) := x( n)

1

x ( n) := x ( n + ) 1 = x( n + )

1

2

1

x ( n) := x ( n + ) 1 = x( n + 2)

3

2

..................................................

x ( n) :

m

= x (

m−

n + )

1 = x( n + m − )

1

1

x ( n + )

1 = x( n + m)

m

x ( n

− a x( n

L

−

+ m − )

1 −

− a x( n + )

1 − a x( n)

m

+ )

1 =

m 1

1

0

x ( n

− a x ( n) L

−

− − a x ( n) − a x ( n) m

+ )

1 =

m 1

m

1

2

0 1

x( n + )

1 = Ax( n),

 x ( n) 

 x (0)   x(0) 

1

1







 



 x ( n)

x (0)

x )

1

(

2



x( n) =

 2

 



, x(0) =

=

 M 

 M  

M









 



 x ( n)

 x (0)

 x( m − )

1 

m



m



W4-2 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

 0

1

0

L

0







L

 0

0

1

0



A =  M

M

M

O

M







 0

0

0

L

1



− a

a

a

L

a

0

− 1 − 2

−





m−1 

m

m 1

M ( z) = z + a

z −

L

−

+ + a z + a

-

wielomian

m 1

1

0

charakterystyczny macierzy A

zi wartości własne A

W4-3 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

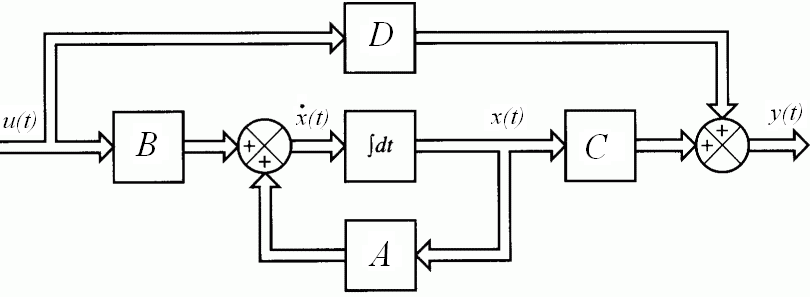
Opis układów dyskretnych w przestrzeni stanów

x(( k + )

1 T ) = Ax( kT ) + Bu( kT ) y( kT ) = Cx( kT ) + Du( kT ) x((k+1)T)

x(kT)

y(kT)

u(kT

1

z

Rozwiązanie:

x(( k + )

1 T ) = Ax( kT ) + Bu( kT ) x( T ) = Ax(0) + Bu(0) x(2 T ) = Ax( T ) + Bu( T ) 2

= A x(0) + ABu(0) + Bu( T ) x 3

( T ) = Ax(2 T ) + Bu(3 T ) =

3

A x(0)

2

+ A Bu(0) + ABu( T ) + Bu(2 T)

.....................................................................

k 1

−

k

k

i 1

−

x( kT ) = Ak x( )

0

k − i 1

+ ∑ A − Bu( i)

+ ∑

−

= A x(0)

A Bu(( k

i) T )

i=0

i 1

=

Operatorowo

zX ( z) − zx(0) = AX ( z) + Bu( z)

−

X ( z) = ( zI − A) 1( zx( ) 0 + Bu( z))

1

−

Ak = Z { z( zI − A) 1

− } macierz tranzycyjna

1

−

−1

Ak

= Z ({ zI − A) 1−}

Y ( z) =

−

CX ( z) + Du( z) = C( zI − A) 1( zx( ) 0 + Bu( z))+ Du( z) x( )

0 =

−

0 ⇒ Y ( z) = [ C( zI − A) 1 B + D] u( z)

W4-4 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

G( z =

−

C( zI − A) 1

)

B + D macierz transmitancji dyskretnych

W4-5 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

Postać modalna rozwiązania:

A ma n różnych wartości własnych zi Macierzą przekształcenia przez podobieństwo do postaci diagonalnej jest macierz, której kolumnami są wektory własne:

 z

L

0

0 

 1



 0

z

L

0

2



Λ =

V = [ v

v

L

v

 M

M

O

M 

1

2

n ],







L

0

0

zn 

v

A

= z v

i

i

i i=1,...., n

AV = Λ

V

−1

A = VΛ V

−

V 1 AV = Λ

2

−1

−1

2

−1

A = VΛ V VΛ V

= VΛ V

3

2

−1

−1

3

−1

A = VΛ V VΛ V

= VΛ V

.........................



T

k





L



z

0

0

w 1

 1







k

T

0

z

L

0

−1

 w 2 

k



2



k

k

−1

V

=: W =

A = VΛ V Λ = 







M

M

O

M

,

M











T



k

L

0

0

z 

 w 

n 

n 

n

k

k

k

−1

∑( z v w

j )

T

A = VΛ V =

j

j

j=1

k

n

x( kT )

k

i 1

−

∑( zj ) k

T

= A x(0) + ∑ A Bu(( k − i) T ) ==

v w x( )

0

j

j

i=0

j 1

=

k

n

+ ∑∑( −

z

−

j ) i 1 v wT Bu(( k i) T )

j

j

i 1

= j=0

n

n

k

∑(

T

i 1

z

+

−

∑ v w ∑

−

j

j

( zj) Bu(( k i) T) i ) k

T

=

v w x(0)

i

i

i 1

=

j 1

=

i=0

część swobodna

część wymuszona

W4-6 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

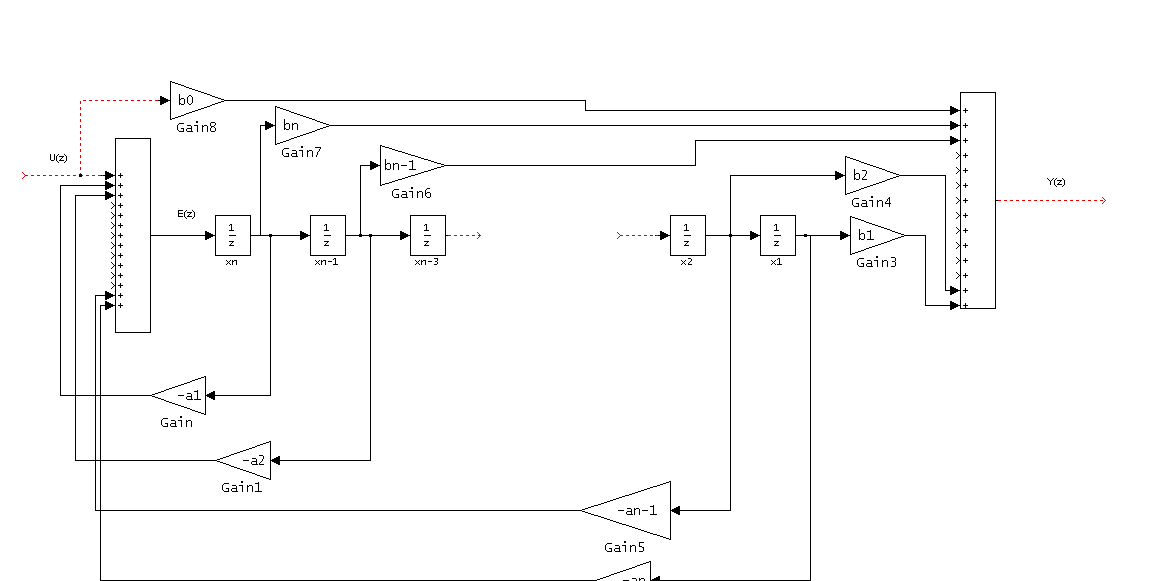
Wyznaczanie opisu w przestrzeni stanów

(I wariant metody bezpośredniej)

~

~

~

n

n

n−1

n−2

Y ( z)

b z

~

b z

1

+ b z

2

+L+ b

0

+ b z −1

1

+L+ bn

G( z) =

=

n

b 0 +

n

n

=

−

U ( z)

z + a z −1

n

n

z + a z 1

1

+L+ a

1

+L+ an

n

~

~

~

~

~

~

b = b − a b , b = b − a b ,L, b = b − a b 1

1

1 0

2

2

1 0

n

n

n 0

−1

−2

− n

~

b z

1

+ b z

2

+L+ b z

n

G( z) = b 0 +

−1

− n

1+ a z

1

+L+ a z

n

~

( )

Y ( z) = b U ( z) 0

+ ( −1

−2

−

U z

n

b z

1

+ b z

2

+L+ b z

n

)

−1

− n

1+ a z

1

+L+ a z

n

U ( z)

E( z) =

−1

− n

1+ a z

1

+L+ a z

n

E( z) = U ( z) − (

1

−

2

a z

+ a z− +L+ a z− n E z

1

2

n

) ( )

X ( z) = z− nE( z) 1

X ( z) = zX ( z)

− n 1

= z + E( z),L, X ( z) = zX ( z) 1

= z− E( z)

2

1

n

n 1

−

wtedy:

 x (( k + )

1 T ) 

 0

1

L

0  x ( kT ) 

0

1

1









  



M





O

O



M

 M

=

+

u( kT )

 x (( k

L

−

+ )

1 T )

 0

0

1  x

( kT )

0

n 1

n 1







 −

  

 x (( k + )

1 T ) 

− a

− a

L

−

− a  x ( kT)  1

 

n

n

n 1

1

n

 x ( kT ) 

1





M

y( kT ) = [ b

b

L

b 



−

+ b u kT

n

n 1

1 ]

~ ( )

 x ( kT )

0



n 1

 −



 x ( kT ) 

n

W4-7 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

Liniowe przekształcenie zmiennych stanu:

Opis układu w postaci:

x(( k + )

1 T ) = Ax( kT ) + Bu( kT ) y( kT ) = Cx( kT ) + Du( kT )

x(kT) – wektor zmiennych stanu o wymiarze nx1,

u(kT) – wektor wejść/sterowań o wymiarze rx1

y(kT) – wektor wyjść o wymiarze mx1

wprowadzamy nowe zmienne stanu:

Pq( kT ) = x( kT ), det P ≠ 0

Pq(( k + 1 )T ) = APq( kT ) + Bu( kT ) nowe równanie s tan u

y( kT ) = CPq( kT ) + Du( kT ) nowe równanie wyjścia

W4-8 Notatki do wykładu „Sygnały dyskretne” Instytut Automatyki PŁ

−1

−1

q(( k + 1 )T ) = P APq( kT ) + P Bu( kT ) nowe równanie s tanu

y( kT ) = CPq( kT ) + Du( kT ) nowe równanie wyjścia

%

%

%

−1

%

−1

q(( k + 1 )T ) = Aq( kT ) + Bu( kT ) A = P AP, B = P B

y( kT ) = C% q( kT ) + Du( kT ) C% = CP

wartości własne nowej macierzy stanu są takie same jak starej!!

Jaka będzie transmitancja:

−

−

G(

% z ) = C%( zI − A%) 1 B% + D = CP( zI − P− AP) 1

1

1

P− B + D =

−

−

−

−

−

= CP  P



( zI − A) 1

P P B



+ D = CPP ( zI − A) 1

1

1

1

1

PP− B + D =

−

= C ( zI − A) 1 B + D = G( z )

−

−

−

bo ( MN ) 1

1

1

=

N M

liniowe przekształcenie zmiennych stanu nie zmienia transmitancji!!