Gabriela Siemiaszko Doświadczenie nr 3
27.04.10.
Wahadło matematyczne
Wstęp
Moim zamiarem było zbadanie zależności okresu drgań wahadła matematycznego od długości i zawieszonej masy. Uzyskam to, posługując się wzorem:
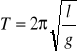
(1)
gdzie:
T - okres drgań [s]
l - długość wahadła [mm]
g - przyspieszenie ziemskie [m/s2].
Dopasowałam zależność liniową, przekształcając wzór (1):
![]()
(2)
y = a x
Chcę także wyznaczyć przyspieszenie ziemskie i oczekuję, że wyniesie 9,81 m/s2.
Doświadczenie
Zawiesiłam metalową kulkę (m1) na cienkiej nici. Zmierzyłam katetometrem z dokładnością do 1 mm wysokość, na jakiej znajdował się punkt zawieszenia nici (h0). Każdorazowo mierzyłam z taką samą dokładnością wysokość położenia środka masy przedmiotu (hi), zmieniając to położenie. Ich różnica stanowiła długość wahadła (l) (wzór nr 3 w dodatku), której błąd wyniósł 1,41 mm (wzór nr 4 w dodatku).
Dokonawszy pomiaru długości wahadła, odchylałam kulkę na odległość około 5 cm i mierzyłam zegarem elektronicznym długość trwania dziesięciu okresów. Dokładność stopera wynosiła 0,1s. Powtarzałam mierzenie czasu trwania dziesięciu okresów pięciokrotnie dla siedmiu różnych długości wahadła, aby oszacować błąd przypadkowy. Pomiary zniekształcone przez błąd przypadkowy pomijałam i powtarzałam pomiar.
Te same czynności powtórzyłam dla kulki o większej masie (m2). Zważyłam kulki wagą laboratoryjną.
Pomiary umieściłam wraz z wynikami obliczeń w tabelach 1 i 2 w dodatku.
Analiza danych eksperymentalnych
Na wykresach przedstawiam zależność okresu drgań podniesionego do kwadratu od długości wahadła dla obydwu kulek . Pominęłam słupki błędów wzdłuż osi, gdyż były mało widoczne.
Wykres 1. Zależność T2 od l dla lżejszej kulki m1. Współczynniki dopasowania wynoszą: a= 0,004±0,00015 [s2/mm] i b=0,012±0,08 [s2]. Funkcja przyjmuje postać y=0,004x+0,012.
Wykres 2. Zależność T2 od l dla cięższej kulki m2. Współczynniki dopasowania wynoszą: a= 0,004±0,000064 [s2/mm]
i b=0,01±0,03 [s2]. Funkcja przyjmuje postać y=0,004x+0,01.
Moje dane powinny spełniać zależność liniową opisaną wzorem (2), lecz nie jest tak w granicach błędów. Wyznaczone proste w granicach błędu przechodzą przez zero układu współrzędnych. Współczynnik b w granicach błędu jest równy zeru.
Ze wzoru nr 10 w dodatku wyliczam wartość przyspieszenia ziemskiego, a ze wzoru nr 11 w dodatku jego błędy. Wynosi ono g1=10,054±0,4[m/s2] i g2=9,93±1,16 [m/s2].
Masy kulek wynosiły: m1=139,5±0,02[g], m2=67±0,02[g]. Błąd pomiaru to masa najlżejszego odważnika. Wykres 3. przedstawia zależność okresu drgań od masy. W granicach błędu punkty układają się na linii prostej.
Wykres 3. Zależność okresu drgań od masy.
Dyskusja i wnioski
Kwadrat okresu drgań wahadła jest wprost proporcjonalny do długości wahadła. Niedopasowaniu zależności liniowej w granicach błędu być może winne jest nieuwzględnienie przeze mnie 0,2-sekundowego refleksu eksperymentatora i inne błędy systematyczne.
Wyliczona wartość przyspieszenia ziemskiego jest stała w granicach błędu dla obydwu zestawów doświadczalnych.
Okres drgań wahadła nie zależy od masy kulki.
Dodatek
Powyżej kolumn tabeli 1 umieściłam informacje, jakim wzorem z dodatku wartość została policzona. Analogicznie dla tabeli 2.
wzór 5 wzór 6 wzór 8 wzór 9 wzór 7
n |
hi [mm] |
t10 [s] |
t10śr [s] |
L [mm] (x) |
T2 [s 2] (y) |
dt10 [s] |
dt10śr [s] |
dT2 [s2] |
||||
1 |
629 |
11,5 |
11,7 |
11,7 |
11,6 |
11,6 |
11,62 |
349 |
1,35 |
0,068 |
0,026 |
0,01 |
2 |
574 |
12,7 |
13 |
12,8 |
12,8 |
12,9 |
12,84 |
404 |
1,65 |
0,093 |
0,035 |
0,01 |
3 |
532 |
13,2 |
13,3 |
13,1 |
13 |
13,1 |
13,14 |
446 |
1,73 |
0,093 |
0,035 |
0,01 |
4 |
471 |
14,2 |
14,4 |
14,4 |
14,2 |
14,3 |
14,3 |
507 |
2,04 |
0,082 |
0,031 |
0,01 |
5 |
430 |
14,7 |
14,5 |
14,6 |
14,7 |
14,7 |
14,64 |
548 |
2,14 |
0,073 |
0,028 |
0,01 |
6 |
368 |
15,6 |
15,6 |
15,4 |
15,8 |
15,5 |
15,58 |
610 |
2,43 |
0,121 |
0,046 |
0,01 |
7 |
328 |
16 |
15,9 |
16 |
16 |
15,8 |
15,94 |
650 |
2,54 |
0,073 |
0,028 |
0,01 |
Tabela 1. Dane pomiarowe i wyniki obliczeń dla kulki m1.
n |
hi [mm] |
t10 [s] |
t10śr [s] |
L [mm] (x) |
T2 [s2] (y) |
dt10 [s] |
dt10śr [s] |
dT2 [s2] |
||||
1 |
667 |
11 |
11,1 |
11,2 |
11,1 |
10,9 |
11,06 |
311 |
1,22 |
0,093 |
0,035 |
0,01 |
2 |
627 |
11,9 |
12,1 |
11,9 |
12 |
12 |
11,98 |
351 |
1,44 |
0,068 |
0,026 |
0,01 |
3 |
556 |
13 |
12,9 |
12,9 |
12,9 |
13 |
12,94 |
422 |
1,67 |
0,045 |
0,017 |
0,00 |
4 |
489 |
14 |
13,9 |
14,1 |
13,9 |
14,2 |
14,02 |
489 |
1,97 |
0,106 |
0,040 |
0,01 |
5 |
429 |
14,8 |
14,9 |
14,8 |
14,7 |
14,7 |
14,78 |
549 |
2,18 |
0,068 |
0,026 |
0,01 |
6 |
387 |
15,5 |
15,3 |
15,5 |
15,5 |
15,3 |
15,42 |
591 |
2,38 |
0,089 |
0,034 |
0,01 |
7 |
288 |
16,6 |
16,6 |
16,4 |
16,6 |
16,6 |
16,56 |
690 |
2,74 |
0,073 |
0,028 |
0,01 |
Tabela 2. Dane pomiarowe i wyniki obliczeń dla kulki m2.
Dostosowane do danych wzory:
l=ho-hi
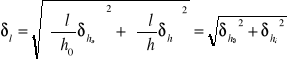
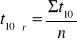
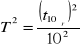
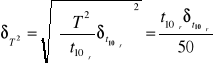
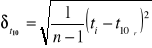
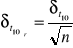
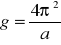
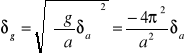
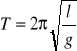
![]()
Wyszukiwarka
Podobne podstrony:
2011 09 22 Rozkaz nr 904 MON instrikcja doświadczenie w SZ RP
Doświadczenie nr 2 Wyznaczenie współczynnika załamania szkła i wody, Studia, Geodezja, III SEMESTR,
Ćwiczenie nr 2 Doświadczalne wyznaczanie masowego momentu?zwładności
doswiadczenie nr 3, fiza laborki
Sprawozdanie nr 13, Metody doświadczalne
ćwiczenia nr 9, 09. Doswiadczenia a rozwoj moralny jednostki
2011 09 22 Rozkaz nr 904 MON instrikcja doświadczenie w SZ RP
Chmielowski Sztuka i doswiadczenie (Estetyka i krytyka nr 9 10)
DOSWIADCZENIE NR 1 FIZYKA LABORKI
Masaz nr 7
Wykład nr 4
Projekt nr 1piątek
TEST NR 5
Zajecia Nr 3 INSTYTUCJE SPOLECZNE
Wykład nr 7
zestaw nr 2
więcej podobnych podstron