CIĄG ARYTMETYCZNY

(2, 4, 6, 8, 10)

ciąg skończony

(2, 5, 8, 11, 14, ...)

ciąg nieskończony

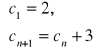
c₂= c₁+3=5

c₃= c₂+3=8

c₄= c₃+3=11

c₅=14

rekurencyjna definicja ciągu

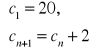
c₂= c₁+2=20+2=22

c₃= c₂+2=22+2=24

c₄= c₃+2=24+2=26

c₅=28

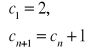
c₂= c₁+1=3

c₃= c₂+1=4

c₄= c₃+1=5

c₅=6

(a₁, a₂, a₃, ...)

JEŻELI CIĄG JEST ARYTMETYCZNY O RÓŻNICY r , TO DLA KAŻDEGO n∈N\{0}

c_n= c₁+(n-1)r

Własności ciągu

c_k-1+ c_k+1

c_k=--------- dla k=2,3,4,…

2

Jeżeli S jest sumą n początkowych wyrazów ciągu arytmetycznego (c), to

n( c₁+ c_n)

S_n=-------------

2

W ciągu arytmetycznym skończonym

(a₁, a₂, a₃, ...) o n wyrazach suma dwóch wyrazów jednakowo oddalonych od początku i końca ciągu jest stała i równa a₁+ a_n

CIĄG GEOMETYCZNY

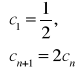
c₂=2 c₁=1

c₃=2 c₂=2

c₄=2 c₃=4

c₅=8

a₂= a₁q

a₃= a₂q= a₁q²

a₄= a₃q= a₁q³

a_n= a₁q^n-1

Każde trzy wyrazy dowolnego ciągu geometrycznego (a)spełniają dla k=2,3,4,…

Jeżeli S jest sumą n początkowych wyrazów ciągu geometycznego (c), to

c₁(1- qⁿ)

S_n=-------------

1 - q

---