CIĄG ARYTMETYCZNY

    Ciąg liczbowy nazywamy ciągiem arytmetycznym, gdy różnica między dowolnym wyrazem ciągu, a wyrazem bezpośrednio go poprzedzającym jest stała - oznaczamy ją przez r i nazywamy różnicą ciągu arytmetycznego.

np.    a_n = ( 1, 2, 3, 4, 5, 6, 7 ,8 )
a₂ - a₁ = 2 - 1 = 1
a₃ - a₂ = 3 - 2 = 1
a₄ - a₃ = 4  - 3 = 1
itd.

Różnica r = 1
Ten ciąg jest arytmetyczny.


np.    a_n = ( 1, 2, 3, 4, 5, 7, 6 , 21, 15 )
a₂ - a₁ = 2 - 1 = 1
a₃ - a₂ = 3 - 2 = 1
a₄ - a₃ = 4 - 3 = 1
a₅ - a₄ = 5 - 4 = 1
a₆ - a₅ = 7 - 5 = 2
itd.

Różnica nie jest stała
Ten ciąg nie jest arytmetyczny.

Przykłady:

Zad. 1

Czy ciąg a_n = n jest arytmetyczny?

   Rozwiązanie:
     Należy sprawdzić, czy różnica a_n+1 - a_n jest stałą  liczbą. (Aby wyznaczyć wyraz (n+1) do wzoru na a_n podstawiamy zamiast n n+1)

     Utwórzmy tę różnicę   

     a_n = n    

a_n+1 = n + 1 

             a_n+1 - a_n = n + 1 - n = 1    

Niezależnie od wartości n - różnica wynosi 1, czyli ciąg a_n = n jest arytmetyczny.


Zad. 2
Czy ciąg b_n = n² + 1 jest arytmetyczny?
 

Rozwiązanie:
     Należy sprawdzić, czy różnica b_n+1 - b_n jest stała.

       Utwórzmy wyraz b_n+1  (wstawiamy n +1 w miejsce n we wzorze n² + 1)       

         b_n+1 = (n + 1)² + 1         

    

         Teraz tworzymy różnicę:
      b_n+1 - b_n = (n + 1)² + 1 - (n²+ 1) =(n + 1)² + 1 - n² - 1 = n² + 2n + 1 +1 - n² - 1= 2n +1    

    
Różnica nie jest liczbą stałą! Wyrażenie 2n +1 zależy od n, przyjmuje różne wartości w zależności od tego, ile wynosi n.
Zatem ciąg b_n = n² + 1 nie jest arytmetyczny.

Ciąg arytmetyczny jednoznacznie wyznaczają jego pierwszy wyraz a₁ i różnica r .

W ciągu arytmetycznym o różnicy r i pierwszym wyrazie a₁ kolejne wyrazy są równe:

a₂ = a₁ + r

a₃ = a₂ + r = a₁ + r + r = a₁ + 2r

a₄ = a₃ + r = a₁ + 2r + r = a₁ + 3r

itd.

Z równości tych wynika wzór (ogólny ciągu) na n-ty wyraz ciągu arytmetycznego

a_n = a₁ + (n − 1)r.

Wykorzystując ten wzór możemy wyznaczyć każdy wyraz ciągu arytmetycznego (mając a₁ i r), a także wyznaczyć ciąg mając dane inne wyrazy ciągu.

Przykład

1) Pierwszym wyrazem pewnego ciągu arytmetycznego jest liczba -3, a piątym liczba 15. Znajdź drugi, trzeci i czwarty wyraz tego ciągu.

Rozwiązanie

a₁ = -3

a₅ = 15

a₅ = a₁ + (5-1)r

a₁ + (5-1)r = 15

-3 + 4r = 15

4r = 15 + 3

4r = 18 /: 4

r = 4,5

a₂ = a₁ + r

a₂ = -3 + 4,5

a₂ = 1,5

a₃ = a₁ + 2r

a₃ = -3 + 2 ⋅ 4,5

a₃ = -3 + 9

a₃ = 6

a₄ = a₁ + 3r

a₄ = -3 + 3 ⋅ 4,5

a₄ = -3 + 3 ⋅ 4,5

a₄ = -3 + 13,5

a₄ = 10,5.

2) W ciągu arytmetycznym dane są a₅ =8 i a₁₂ = -6.Oblicz a₂₅

Rozwiązanie

Korzystając ze wzoru na n-ty wyraz ciągu arytmetycznego a_n = a₁ + (n − 1)r , zapisujemy

wyrazy a₅ i a₁₂

a₅ =a₁ + 4r

i a₁₂ = a₁ + 11r

8 = a₁ + 4r

-6 = a₁ + 11r

Z otrzymanych równań budujemy układ, z którego wyznaczamy a₁ i r, czyli wartości które jednoznacznie określają ciąg arytmetyczny.

+

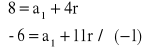
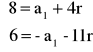
14 = -7r /:(-7)

r = -2

8 = a₁ + 4⋅ (-2)

a₁ = 16

a₂₅ = a₁ + 24r

a₂₅ = 16 + 24⋅ (-2)

a₂₅ = 16 - 42

a₂₅ = -26.

W ciągu arytmetycznym każdy wyraz (oprócz pierwszego i ostatniego) jest równy średniej arytmetycznej dwóch sąsiednich wyrazów:

Przykład

Dla jakiej wartości x liczby
są kolejnymi wyrazami ciągu arytmetycznego?

Rozwiązanie

Korzystając z powyższej własności otrzymujemy

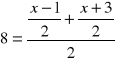
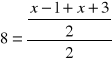
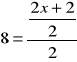
/⋅2

16 =
/⋅2

32 = 2x +2

32 - 2 = 2x

30 = 2x /:2

x = 15.

Dla x = 15 liczby
tworzą ciąg arytmetyczny.

Jeśli zsumujemy n początkowych kolejnych wyrazów ciągu arytmetycznego, wówczas otrzymujemy S_n = a₁ + a₂ + a₃ + ... + a_n (wzór na sumę n początkowych, kolejnych wyrazów ciągu arytmetycznego), gdzie

Przykłady

1) Oblicz sumę jedenastu początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie a₁ = -12 i różnicy r = 0,2.

Rozwiązanie

n = 11 a₁ = -12 r = 0,2.

2) Oblicz sumę wyrazów od dziesiątego do trzydziestego dla ciągu arytmetycznego, w którym a₁ = -5 i różnicy r = 0,5.

Rozwiązanie

a₁₀ + a₁₁ + ... + a₃₀ = S₃₀ - S₉

a₃₀ = -5 + 29 ⋅ 0,5

a₃₀ = -5 + 14,5

a₃₀ = 9,5

a₉ = -5 + 8 ⋅ 0,5

a₉ = -5 + 4

a₉ = -1

S₃₀ - S₉ =

Ćwiczenie 1

Rozwiąż zadania:1-9, 11-16,21-23,29, str. 175-179 z podręcznika.

---