Definicja Ciągu
Arytmetycznego

Ciągiem arytmetycznym nazywamy ciąg

liczbowy, w którym różnica między dowolnym
wyrazem, a wyrazem .który go bezpośrednio
poprzedza jest stała.

Na przykład :



ciąg

: 1, 3, 5, 7, 9, ...

jest

arytmetyczny (jego różnicą jest 2)



ciąg:

1, 3, 4, 5, 7, 8, 9, 11, 12, ...

nie jest

(3=1+2, lecz 4=3+1).

Każdy wyraz ciągu arytmetycznego - oprócz

pierwszego - otrzymujemy dodając do
poprzedniego tą samą liczbę . . Liczbę
nazywa się różnicą ciągu.

W ciągu arytmetycznym różnica między

kolejnymi wyrazami jest stała:



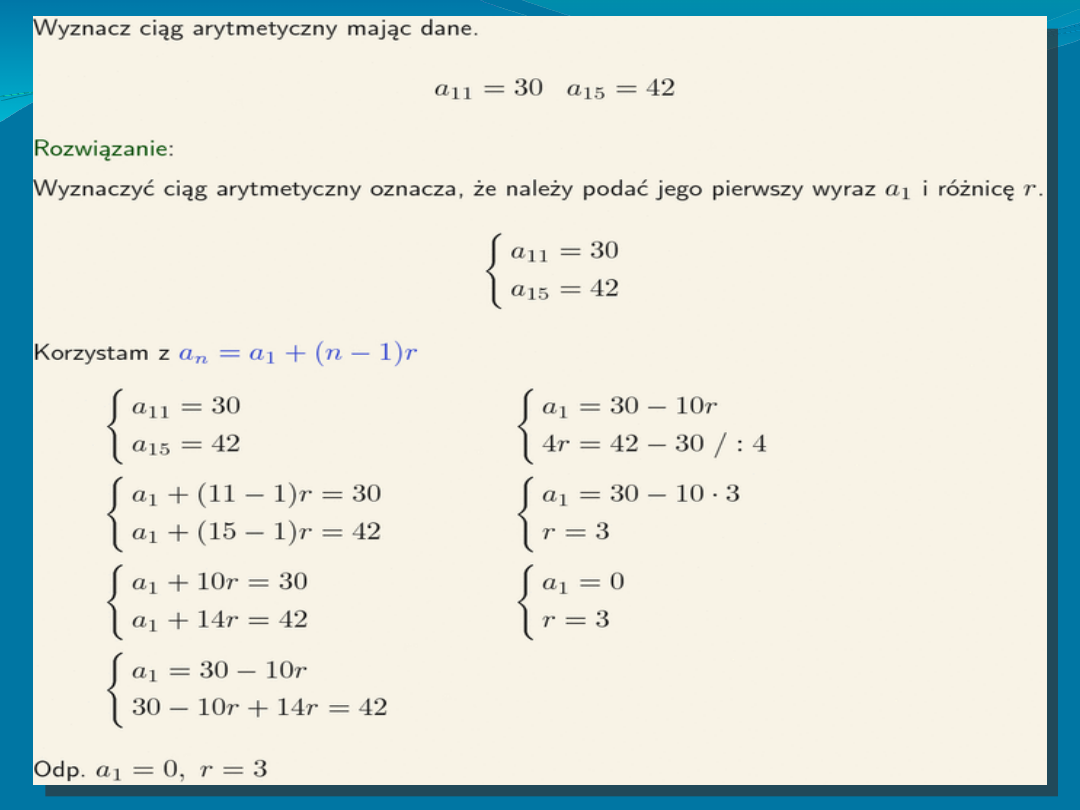
Ciąg arytmetyczny jest określony, jeżeli znamy

jego wyraz pierwszy i różnicę . Wtedy :



Zatem, aby wyznaczyć pierwszy wyraz

ciągu arytmetycznego oraz jego różnicę
wystarczy znać dwa wyrazy tego ciągu.

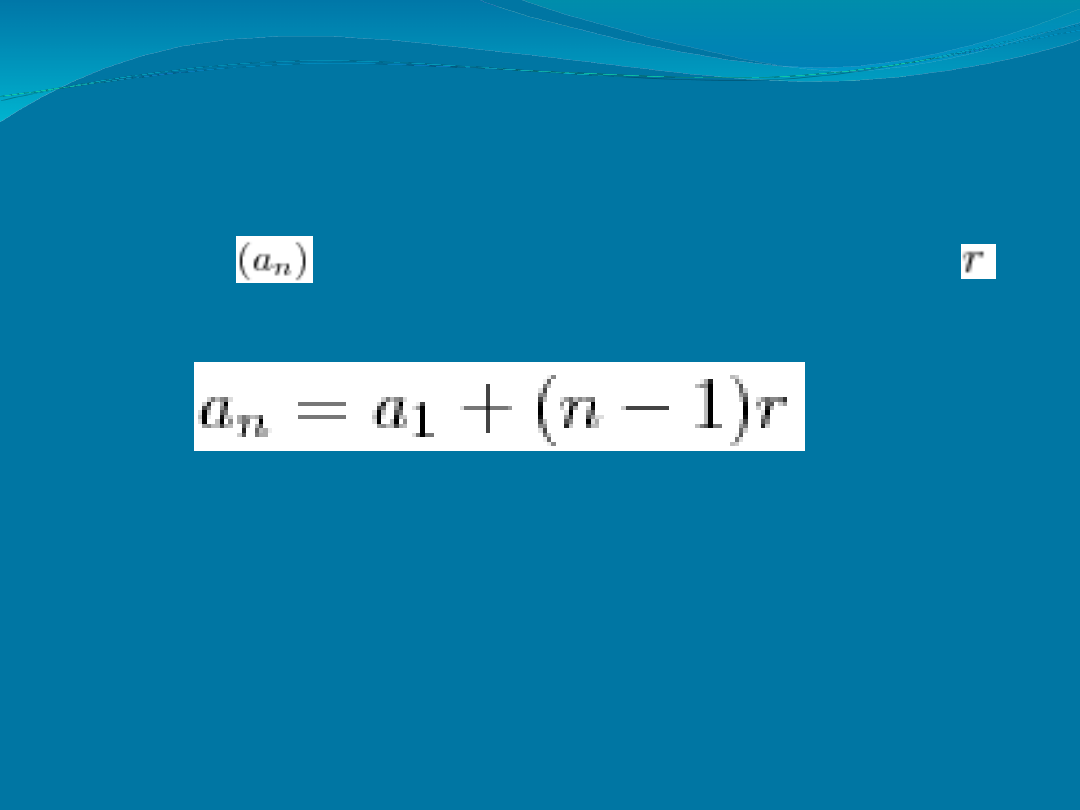
Wyraz ogólny ciągu
arytmetycznego

Jeżeli ciąg jest ciągiem arytmetycznym o

różnicy

to prawdziwy jest wzór :

Własności Ciągu
Arytmetycznego



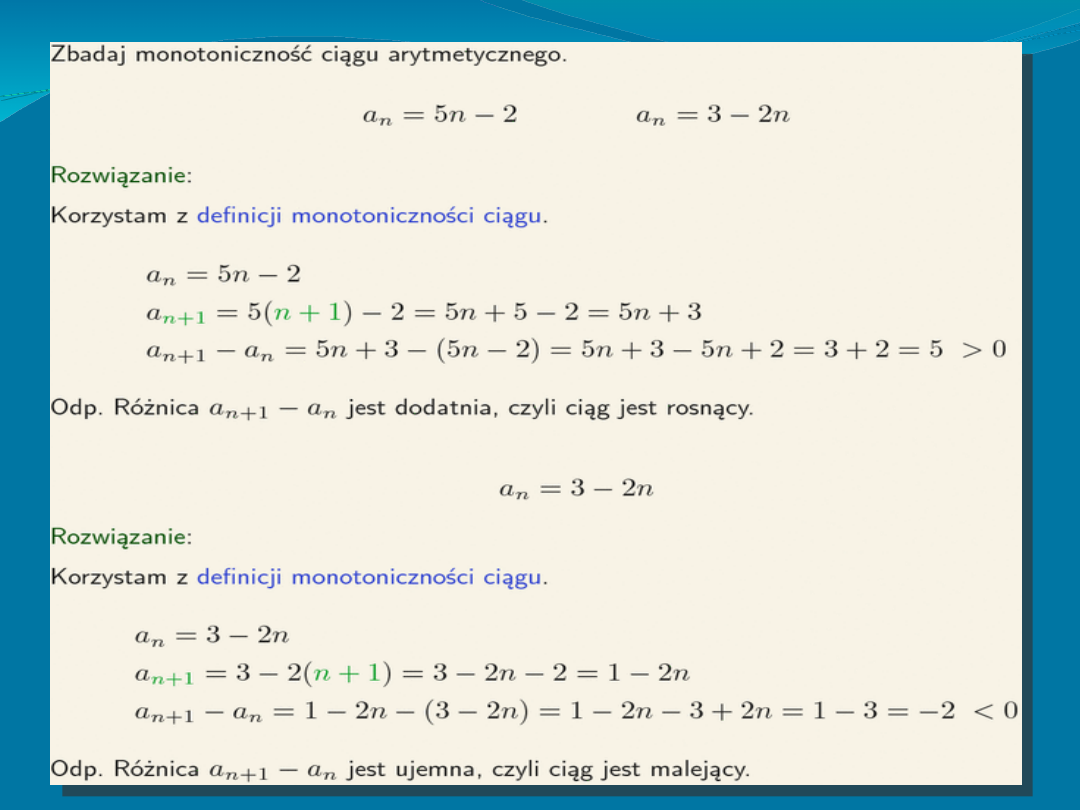
Monotoniczność - ciąg arytmetyczny jest:

-

Rosnący, gdy

-

Malejący, gdy

-

Stały, gdy

Np

. 1,3,5,7,9

<--- ciąg rosnący

-1,-3,-5,-7,-9 <

--- ciąg malejący

0,0,0,0,0,0

<---- ciąg stały



Każdy wyraz ciągu arytmetycznego,

poczynając od drugiego, jest średnią
arytmetyczną jego dwóch sąsiednich wyrazów
:



Ciąg arytmetyczny może być nieskończony

lub skończony, ale ciąg skończony musi mieć
co najmniej 3 wyrazy.

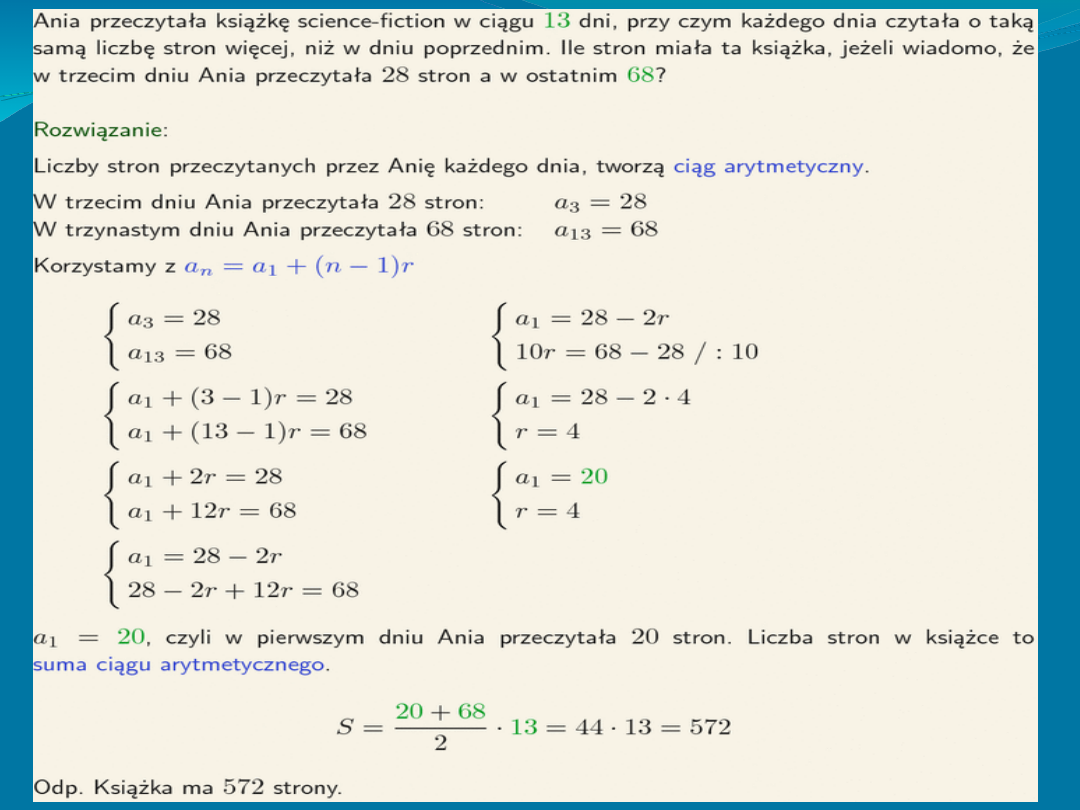
Suma Częściowa ciągu

Arytmetycznego

Suma początkowych wyrazów ciągu

arytmetycznego równa jest iloczynowi liczby
wyrazów przez średnią arytmetyczną wyrazu
pierwszego i ostatniego.

O pewnych ciągach

Arytmetycznych



Kolejne liczby naturalne 1,2,3, ... , , ...

tworzą ciąg arytmetyczny o różnicy 1,

Ze wzoru na otrzymujemy:

czyli wzór na sumę kolejnych liczb naturalnych

od 1 do Suma taka pojawia się często
nie tylko w matematyce, czy fizyce.



Weźmy sumę kolejnych liczb

nieparzystych

oczywiście

KONIEC

Wykonał Artur Chałubiński

kl. 2 Atl