CIĄG ARYTMETYCZNY

Pojęcie ciągu arytmeytcznego

• Ciąg arytmetyczny to taki ciąg liczbowy, w

którym różnica między danym wyrazem, a
wyrazem bezpośrednio go poprzedzającym
jest stała i równa r.

• Wzór ogólny:
• a

n

=a

1

+(n-1)r

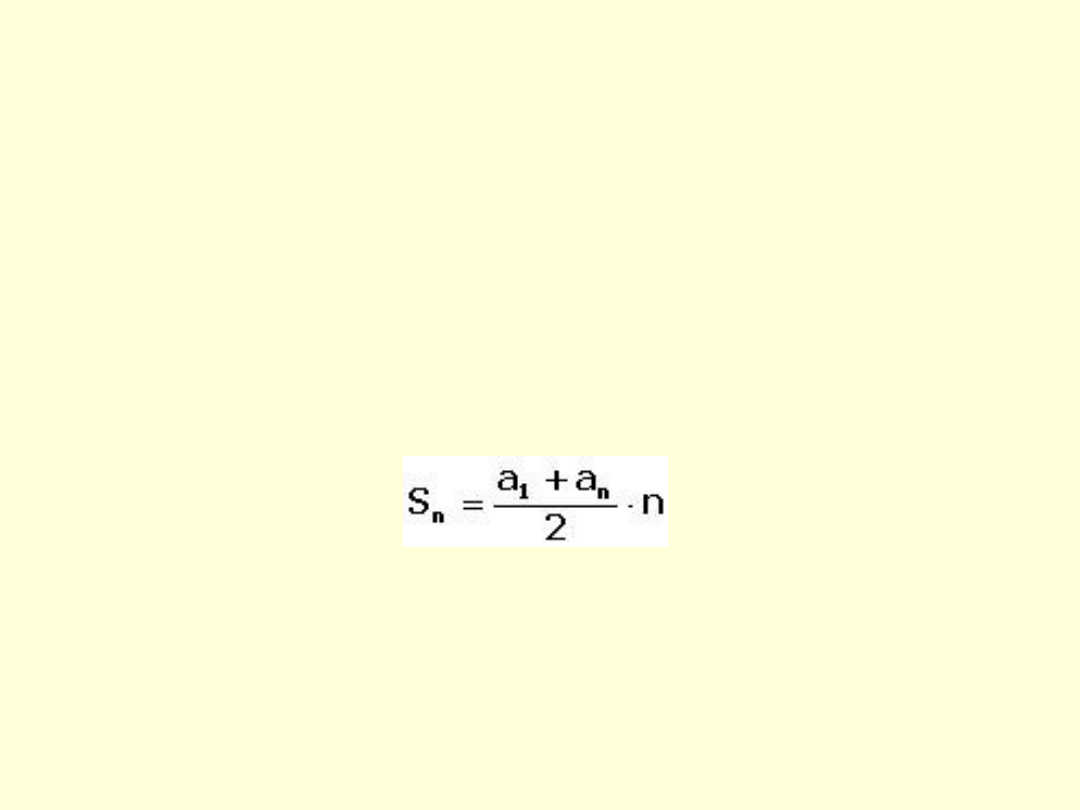
Suma n-początkowych

wyrazów ciągu

arytmetycznego

• Suma n początkowych wyrazów ciągu

arytmetycznego (a

n

) wyraża się wzorem:

Monotoniczność ciągu

• r > 0 to ciąg jest rosnący
• r < 0 to ciąg jest malejący
• r = 0 to ciag jest stały

Zadania

• Zad.1
Oblicz pięć początkowych wyrazów ciągu:

a

n

=5

n

-3

a

1

=5*1-3=2

a

2

=5*2-3=7

a

3

=5*3-3=12

a

4

=5*4-3=17

a

5

= 5*5-3=22

• Zad.2

W ciągu arytmetycznym a

1

= -5 i r=6.

Oblicz: a

7

i a

100

.

a

7

=a

1

+6r= -5+36=31

a

100

=a

1

+99r= -5+594=589

• Zad.3
Ile jest wszystkich liczb trzycyfrowych?
100,101,102,103…,999 – c.a.
a

1

=100

r=1
a

n

=999

n=?
a

n

=a

1

+(n-1)r

999=100+(n-1)*1
999=99+n
n=900
Odp:Tych liczb jest 900.

• Zad.4

Wyznacz różnicę r ciągu arytmetycznego
mając dane a

1

= 7 i a

29

= 119.

Rozwiązanie:
a

n

= a

1

+ (n-1)r

a

29

= a

1

+ (29-1)r

a

1

= 7 i a

29

= 119, więc

119 = 7 + 28r
112 = 28r /:28
r = 4

Odp. Różnica ciągu wynosi 4.

• Zad.5
Między liczby 4 i 22 wstaw pięć liczb tak, aby

wraz

z danymi liczbami tworzyły ciąg arytmetyczny.
Wstawione liczby nazwijmy a, b, c, d,e.
a = 4 + r
b = a + r = 4 +2r
c = b + r = 4 +3r
d = c + r = 4 +4r
e = d + r = 4 +5r
22 = e + r = 4 +6r
22 = 4 + 6r
22 – 4 =6r
18 = 6r /:6

r = 3
a =4 + r = 4 +3 =7
b = 4 +2r = 4 + 6 = 10
c = 4 + 3r = 4 +9 =13
d = 4 + 4r = 4 + 12 = 16
e = 4 + 5r = 4 +15 = 19.
Odp. Są to liczby 7, 10, 13, 16 i 19.

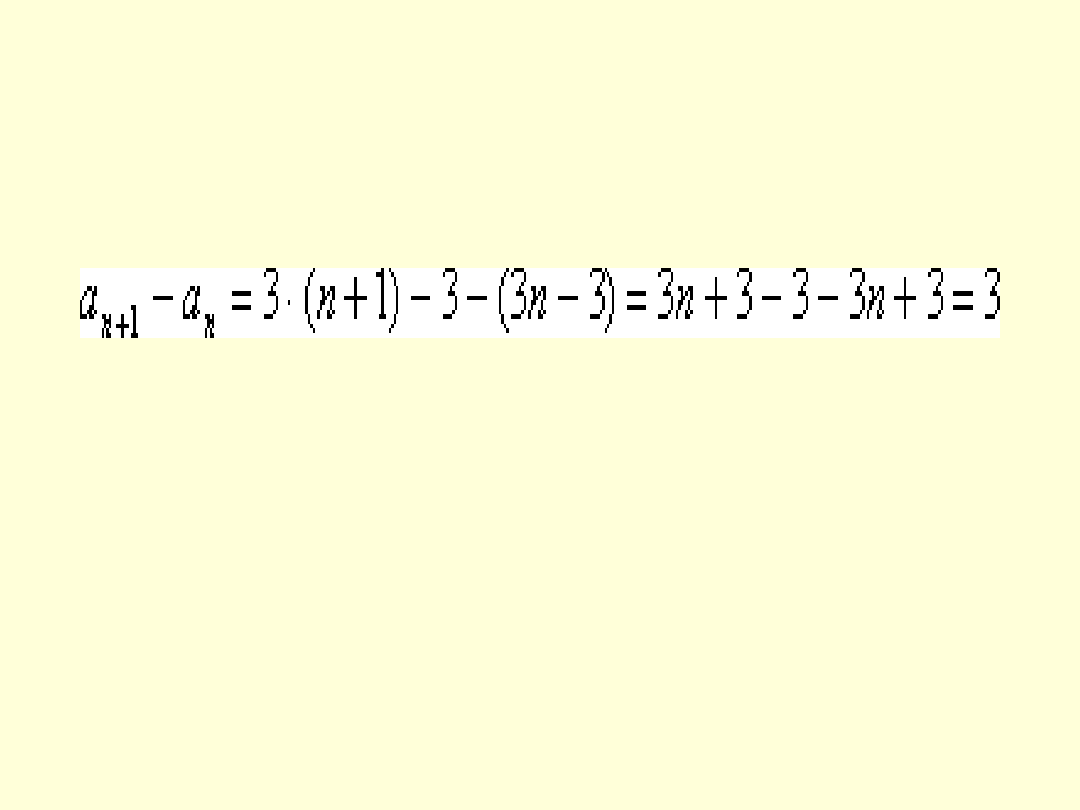
• Zad.6
Sprawdź czy ciąg a

n

= 3

n

– 3 jest

ciągiem

arytmetycznym.

Odp: Jest to ciąg arytmetyczny

• Zad.7
Wyznacz n-ty wyraz ciągu

arytmetycznego.

a

1

=10

n=12
r=15

a

n

=a

1

+(n-1)r

a

12

=10+(12-1)*15

a

12

=10+11*15

a

12

=175

Odp: a

12

=175

• Zad.8
Oblicz n jeśli:
S

n

=30

a

1

=12

a

n

= -6

60=6n/:6
n=10
Odp: n=10.

• Zad.9
Ile liczb trzeba wstawić między liczby

11 i

80, aby z nich otrzymać ciąg

arytmetyczny,

którego suma wynosi 2002?
Sn=2002
a1=11
an=80
n=?

4004=91n/:91
n=44
44-2=42
Odp: trzeba wstawić 42 liczby.

• Zad.10
Suma częściowa ciągu arytmetycznego
równa się 4

n2

-2

n

. Oblicz a

1

, a

20

i r.

S

n

= 4

n2

-2

n

a

1

=?

a

20

=?

r=?
s1= 4*12-2*1=2
a

1

=2

s

2

= a

1

+a

2

S

2

=4*2

2

-2*2=12

a

1

+a

2

=12

2+a

2

=12

a

2

=10

r=8
a

20

=a

1

+19r

a

20

=2+19*8=2+152=154

Odp:a

1

=2, r=8, a

20

=154.

Bibliografia

•

http://www.maximus.pl/bw-ciag_arytmetyc
zny-127.html

;

•

http://pl.wikipedia.org/wiki/Ci%C4%85g_a
rytmetyczny

;

•

http://www.wsipnet.pl/oip/msl/cz2/u/wc.htm
l

;

•

http://www.interklasa.pl/portal/dokumenty
/tab_mat/ciagi/ciagarytmetyczny.html

;

Koniec