1. Wykaż, że jeżeli ciąg
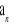
   określony jest wzorem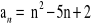
   , to ciąg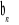
   :
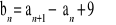
   jest ciągiem arytmetycznym.

2. Załóżmy, że ciąg
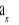
   jest malejącym ciągiem arytmetycznym.

1. wiedząc, że
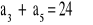
   i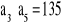
   , oblicz pierwszy wyraz i różnicę tego ciągu.

2. oblicz różnicę między sumą dwudziestu początkowych wyrazów tego ciągu o numerach nieparzystych i sumą wyrazów tego ciągu dziesiątego do dwudziestego włącznie.

3. Różnica ciągu arytmetycznego
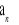
   jest równa 2. Suma p początkowych wyrazów tego ciągu wynosi 21, zaś p-ty wyraz jest równy 9. Natomiast kolejnymi wyrazami ciągu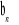
   są te wyrazy ciągu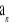
   , w kolejności występowania, które są liczbami podzielnymi przez 5.

1. Znajdź ciąg
   .

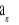
2. Suma ilu początkowych wyrazów ciągu
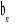
   jest równa 2000?

4. Suma n początkowych wyrazów ciągu
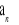
   dla każdego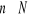
   określona jest wzorem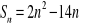
   .

1. Oblicz 30-ty wyraz ciągu
   .

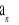
2. Na podstawie definicji wykaż, że
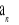
   jest ciągiem arytmetycznym.

3. Znajdź takie trzy kolejne wyrazy ciągu
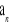
   , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.

5. Suma n początkowych wyrazów ciągu arytmetycznego
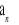
   wyraża się wzorem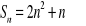
   dla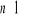
   . Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych: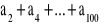
   .

6. Ciąg liczbowy
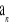
   jest określony dla każdej liczby naturalnej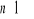
   wzorem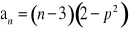
   gdzie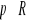
   .

1. Wykaż, że dla każdej wartości p ciąg
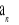
   jest arytmetyczny.

2. Dla p=2 oblicz sumę
   .

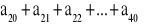
3. Wyznacz wszystkie wartości p, dla których ciąg
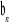
   określony wzorem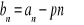
   jest stały.

7. Wykazać, że jeżeli
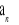
   ciąg jest nieskończonym ciągiem arytmetycznym, to ciąg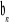
   o wyrazie ogólnym określonym wzorem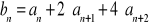
   też jest ciągiem arytmetycznym.

8. Wyznacz ciąg arytmetyczny, którego suma n pierwszych wyrazów jest równa 5n², dla każdego
   .

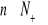
9. W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.

10. Suma n początkowych wyrazów ciągu
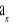
    dla każdego n
    1 określona jest wzorem S_n = 2n² − 14n.

1. Wykaż, że ciąg
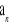
   jest ciągiem arytmetycznym.

2. Wykaż, że jeżeli suma n początkowych wyrazów ciągu dla każdego n ≥ 1 określona jest wzorem S_n = 2n² − 14n + 1, to ciąg ten nie jest arytmetyczny.

11. Dla jakich wartości parametru k równanie
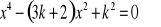
    ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?

12. Ciąg
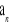
    jest arytmetyczny oraz a₁ = x i a₂ = 4x − 1. Wiedząc, że a₁ + a₂ + a₃ + a₄ + a₅ = 25, oblicz x oraz sumę a ₁₁ + a₁₂ + a₁₃ + …+ a₂₅ .

13. W rosnącym ciągu arytmetycznym stosunek wyrazu szóstego do trzeciego równa się 7, a suma kwadratów wyrazów drugiego i czwartego równa się 40. Wyznacz pierwszy wyraz tego ciągu.

14. Liczby x+ y, 3x + 2y + 1 i 2 x + 5x + 4y tworzą ciąg arytmetyczny. Wyznacz te wartości x, dla których ciąg ten jest rosnący.

15. O liczbach a, b i c wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi
    . Wyznacz największą możliwą wartość wyrażenia
    . Dla jakich liczb a, b i c wartość ta jest osiągana.