Ćwiczenia wytrzymałość 6 - 24 -

Zadanie 22

Dla ramy, której schemat przedstawiono na rys.22, sporządzić wykresy: siły tnącej, siły normalnej i momentu gnącego. Rama składa się z odcinka prostego AC = a i łuku o promieniu R = a. Dane: a = 1,1 m, P = 138 N, α = 48⁰, α_B = 60⁰.

y P α

A C

a R

α_B

B

0 0₁ x Rys.22

Rozwiązanie

1. Określenie wartości reakcji podpór

R_Ay P α

A R_Ax C

a R_B

R α_B

0 0₁ x Rys.22a

B

Warunki równowagi ramy

(a)

(b)

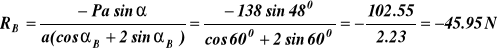
z (a)

z (b)

2. Obliczenia do wykresów - 25 -

Przedział:

M_x

R_Ay R_Ax 0 N

A x

x

T Rys.22b

dla x = 0 M_x=0 = 0

dla x = a M_x=a = - 62,76N·1,1m = - 69.04 Nm

Przedział:
y₁ N 90⁰ + φ T

0 φ

y

M_x

Rsin* R R_B Rys.22c

φ α_B

0 0₁ B x

a = R Rcosφ R-Rcosφ

(c)

(d)

dla * = 0
M_x = 0

dla * = 90⁰

z równań (c) i (d)

dla * = 0,
,

* = 90⁰,

- 26 -

dla * = 0,

dla * = 90⁰,

N = 69,37 N

A C A C

- 22,97N

M_x = - 69,04 Nm

*_N=0

B

0₁ 0₁ B

T = 39,79 N N = 39,79 N

A C

N = R_B(cosα_Bsin* - sinα_Bcos*)

0 = cosα_Bsin*_N=0 - sinα_Bcos*_N=0

tg*_N=0 = tgα_B *_N=0 = α_B = 60⁰

T = -62,76 N

0₁

B T = 22,07 N

Rys. 22c Wykresy momentu gnącego M_x, siły normalnej N, siły tnącej T

Zadanie 23

Podaj współczynnik bezpieczeństwa konstrukcji (rys.23) w stosunku do granicy sprężystości

materiału której wartość *_sp = 300 MPa. Przy obliczaniu współczynnika bezpieczeństwa uwzględnić tylko naprężenia od zginania.

z

z P = 20 kN a - a

a

A B M_g =30 kNm h y

l = 3 m a

Rys.23 h = 100 mm h

Rozwiązanie

Wykres momentów gnących

z T P

M_x

N

A 0 B M_g x

x l - x Rys.23a

Maksymalne wartości momentów będą dla x = 0 i x = l

- 27 -

M_x=0 = 30kNm

A B

M_x=l = -30kNm

Rys.23b

,

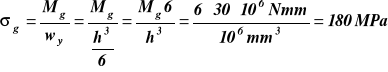
Zadanie 24

Wyznaczyć linię ugięcia pryzmatycznej dwupodporowej belki (rys.24), obciążonej siłą skupioną. Dane: P = 10 kN, a = 1.5 m, b = 1 m, E = 2·10⁵ MPa, pole przekroju belki jest prostokątem o podstawie h = 12 cm i wysokości H = 10 cm, l = a +b.

z z

P

A C B x

H y

a b

Rys.24 h

Rozwiązanie

1. Określenie wartości reakcji

R_Az P R_B

A R_Ax C B x

a b Rys.24a

,

,

gdzie l = a + b

2. Określenie momentów gnących w funkcji x - 28 -

dla
przedział 1 ugięcie w₁

R_Az M_x

R_Ax N

A x ∑ M_i0 = M_x - R_Az x = 0, M_x = R_Az x = Pbx/l

x

T Rys.24b

(a),
(b)

dla
przedział 2 ugięcie w₂

z

a P

R_Az M_x

R_Ax N

A x

x

T Rys.24c

,

(c)

(d)

Warunki brzegowe x = 0, w₁ = 0, z równania (b) D₁ = 0

x = a, w₁′ = w₂′ (a) = (c)

(e)

x = a, w₁ = w₂ (b) = (d)

(f)

x = l, w₂ = 0 z równania (d)

,

- 29 -

,

(g)

Uwzględniając, że D₁ = 0 z rozwiązania równań (e), (f), i (g) otrzymujemy:

,
,
(h)

Kolejność rozwiązania: podstawiamy (e) do (f) i po uwzględnieniu, że D₁ = 0 otrzymujemy równanie z jedną niewiadomą D₂, znając D₂ podstawiamy je do (g) otrzymujemy znowu równanie z jedną niewiadomą C₂, C₁ wyznaczamy z (e).

Maksymalna wartość ugięcia wystąpi tam gdzie w′ = 0, będzie to przedział
bo a>b

podstawiając (h) do (a)

(i)

dla
x = x₁ z równania (i)

Wartość ugięcia dla x = x₁ z równania (b)
podstawiamy C₁

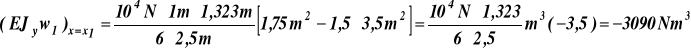
wzór na moment bezwładności pola przekroju (rys.24) względem osi y

wartość momentu pola przekroju

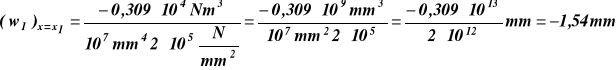
- 30 -

Wykresy (rys.24d): momentu gnącego, kąta ugięcia υ = w′, oraz ugięcia w

z P

x₁

A B x

a b

M_g

w′

w w_max

Rys.24d

---