1. Optymalizacja poszerzenia na prostej

1. Funkcja celu

Za funkcję celu optymalnego projektu poszerzenia międzytorza przyjmujemy stosunek jego całkowitej długości Lc do wartości poszerzenia p która powinna osiągnąć wartość minimalną przy danej prędkości pociągów pasażerskich Vp, danej prędkości pociągów towarowych Vt, oraz przy zachowaniu następujących

warunków:

a <= ap

an <= at (tylko przy typie 2)

ψ <= ψdop

f <= fdop (tylko przy typie 2)

k >= kmin (tylko przy typach 1 i 2)

w >= wmin (tylko przy typie 1)

h ∈ < hmin: hmax > (tylko przy typie 2)

Lc < Lmax

2. Analiza wariantów

1. Dwa łuki odwrotne ze wstawką prostą, bez przechyłki

Warunki terenowe dogodne, czyli:

ap = 0,3 m/s2

Ψdop = 0,3 m/s3

m = 100

wmin = maks ( Vp / 1,8; 30 ) = maks ( 120 / 1,8; 30 ) = maks (66,6667; 30) = 66,6667 m

przyjęto wmin = 67,0 m

kmin = maks ( Vp / 25; 30 ) = maks ( 120 / 2,5; 30 ) = maks ( 48; 30 ) = 48 m

hmin = 30 mm

b = 20 m

p = 2,75 m

hmax = 150 mm

Warunki na minimalny promień łuku:

Ramin = Vp ^ 2 / ( 12,96 * ap ) = 120 ^ 2 / ( 12,96 * 0,3 ) = 3703,7037 m

b = 20 m < w = 67 m dlatego:

Rψmin = 0,0214 * Vp ^ 3 / ( Ψdop * b ) = 0,0214 * 120 ^ 3 / ( 0,3 * 20 ) = 6163,2000 m

R = min ( Ramin; Rψmin ) = ( 3703,7037; 6163,2) = 6163,2 m

przyjęto R = 6200 m

Obliczenie długości całkowitej układu:

Lc = ( 4 * R * p + w ^ 2 - p ^ 2 ) ^ ( 0,5 ) = ( 4 * 6200 * 2,75 + 67,0 ^ 2 - 2,75 ^ 2 )^ (0,5) =269,5949 m

Kąt zwrotu trasy:

γ = arcsin ( Lc / ( 4 * R ^ 2 + w ^ 2 ) ^ ( 0,5 ) ) - arcsin ( w / ( 4 * R ^ 2 + w ^ 2 ) ^ ( 0,5 ) ) = arcsin ( 269,5949508058 / ( 4 * 6200 ^ 2 + 67,0 ^ 2 ) ^ ( 0,5 ) ) - arcsin ( w / ( 4 * 6200 ^ 2 + 67,0 ^ 2 ) ^ ( 0,5 ) ) = 0,936199 ^o

Warunek minimalnej długości części kołowej:

k = pi * R * γ / 180 = 22 / 7 * 6200 * 0,9362 / 180 = 101,3064 m

k = 101,3064 m > kmin = 48 m warunek spełniony

T = R * tg ( γ / 2 ) = 6200 * tg ( 0,93620 / 2 ) = 50,6543 m

Z = Lc / p = 269,5949 / 2,75 = 98,0345

2. Dwa łuki odwrotne z czterema krzywymi przejściowymi z przechyłką

Rmin = ( Vp^2-Vt^2 ) / ( 12,96 * ( ap + at ) ) = ( 120^2-70^2 ) / ( 12,96 * ( 0,5 + 0,3 ) ) = 916,2809 m -> przyjęto 950m

h = ( Vp^2 * at + Vt^2 * ap ) / ( 0,0065 * ( Vp^2-Vt^2 ) ) = ( 120^2 * 0,5 + 70^2 * 0,3 ) / ( 0,00654 * ( 120^2-70^2 ) ) = 139,5463 mm -> przyjęto 140 mm

Obliczamy długość krzywej przejściowej

L`` = max ( L``^Ψ_min ; L``<sup>f</sup><sub>min</sub> ; L``ⁿ_{min )} = max ( 33,33;120 * 140 / 100; 0,7 * ( 950 ) ^ ( 0,5 ) ) = max ( 33,33; 168; 21,57 ) = 168m

ε = arctg ( L / ( 2 * R ) ) = arctg ( 168 / ( 2 * 9500 ) ) = 5,053012 °

Xs = L-R * sin ε = 168-950 * sin ( 0,0882 ) = 84,3264 m

y = L^2 / ( 6 * R ) = 168 ^ 2 / ( 6 * 950 ) = 4,9516 m

n = y - R * ( 1 - cos ( ε ) ) = 4,9516 - 950 * ( 1 - cos ( 0,088192 ) ) = 1,2595 m

Lc`` = 2 * Xs`` + ( 4 * p * ( R + n ) + 4 * Xs^2-p^2 ) ^ ( 0,5 ) = 2 * 84,32645 + ( 4 * 2,75 * ( 950 + 1,2595) + 4 * 84,3264 ^2 - 2,75^2 ) ^ ( 0,5 ) = 365,8840 m

γ`` = arcsin ( ( Lc- 2 * Xs ) / ( ( 4 ( R + n ) ^2 + 4 * Xs^2 ) ^ ( 0,5 ) ) ) - arcsin ( ( 2Xs ) / ( ( 4 ( R + n ) ^2 + 4Xs^2 ) ^ ( 0,5 ) ) ) = arcsin ( ( 365,8840 - 2 * 84,3264 ) / ( ( 4 ( 950 + 1,2595 ) ^2 + 4 * 84,3264 ^2 ) ^ ( 0,5 ) ) ) - arcsin ( ( 2 * 84,3264 ) / ( ( 4 ( 950 + 1,2595 ) ^2 + 4 * 84,3264^2 ) ^ ( 0,5 ) ) ) =0,861259°

α = γ-2 * ε = 0,015032-2 * 0,088192 = -9,2447647625 °

K = R * α = 950 * ( -9,2447647625 * 3,14 / 180 ) = -153,284004 m

Kmin = 48m

K > Kmin

-153,2840 > 48 warunek niespełniony dlatego:

h^Ψ_min = Lmin^Ψ * m / Vp = 33,333 * 100 / 120 = 27,78mm -> przyjęto 30mm

h``_min = max ( h^Ψ_min ; h^utrz_min ) = max ( 30 ; 30 ) = 30mm

R``min = ( 11,8 * Vp^2 ) / ( h''min + 153 * ap ) = ( 11,8 * 120^2 ) / ( 30 + 153 * 0,3 ) = 2238,7352 m -> przyjęto 2250 m

L`` = max ( L``^Ψ_min ; L``<sup>f</sup><sub>min</sub> ; L``ⁿ_{min )} = max ( 33,33;120 * 30 / 100; 0,7 * ( 2250 ) ^ ( 0,5 ) ) = max ( 33,33; 36; 33,20 ) = 36m

ε`` = arctg ( L`` / ( 2 * R`` ) ) = arctg ( 36 / ( 2 * 2250 ) ) = 0,458356 °

Xs`` = L``-R`` * sin ε`` = 36 - 2250 * sin ( 0,458356 ) = 18,0006 m

y''k = L''^2 / ( 6 * R'' ) = 36 ^ 2 / ( 6 * 2250 ) = 0,0960m

n = y - R * ( 1 - cos ( ε ) ) = 0,096 - 2250 * ( 1 - cos ( 0,458356 ) ) = 0,0240 m

Lc`` = 2 * Xs`` + ( 4 * p * ( R + n ) + 4 * Xs^2-p^2 ) ^ ( 0,5 ) =

= 2 * 18,000576 + ( 4 * 2,75 * ( 2250 + 0,0240 ) + 4 * 18,0006 ^2 - 2,75^2 ) ^ ( 0,5 ) = 197,3665 m

γ`` = arcsin ( ( Lc- 2 * Xs ) / ( ( 4 ( R + n ) ^2 + 4 * Xs^2 ) ^ ( 0,5 ) ) ) - arcsin ( ( 2Xs ) / ( ( 4 ( R + n ) ^2 + 4Xs^2 ) ^ ( 0,5 ) ) ) = arcsin ( ( 197,3665 - 2 * 18,0006 ) / ( ( 4 ( 2250 + 0,024 ) ^2 + 4 * 18,0006^2 ) ^ ( 0,5 ) ) ) - arcsin ( ( 2 * 18,0006 ) / ( ( 4 ( 2250 + n ) ^2 + 4 * 18,0006^2 ) ^ ( 0,5 ) ) ) = 1,596554°

α`` = γ``-2 * ε`` = 1,596554-2 * 0,458356 = 0,679841 °

K`` = R`` * α`` = 2250 * 0,011865 = 26,6973 m

Kmin = 48m

K > Kmin

26,6973 > 48 warunek niespełniony dlatego:

ϱ = kmin / k'' = 48 / 26,6973 = 1,7979337912

R''' = ϱ * R '' = 1,7979 * 2250 = 4045,351 m przejęto 4050 m

Lmin''' = 0,7 * ( R ) ^ ( 0,5 ) = 0,7 * ( 4050 ) ^ ( 0,5 ) = 44,5477 m

Lmin'' > = Lmin'''

36 m > = 44,5477 m warunek niespełnony czyli brak rozwiązania

3. Dwa odwrotne łuki paraboliczne, bez przechyłki

Pierwsza iteracja:

Rmin = ( Vp^2 ) / ( 12,96 * ap ) = ( 120^2 ) / ( 12,96 * 0,3 ) = 3703,7037m -> przyjęto 3750m

γ₂ = arccos ( ( 4 * R-p ) / ( 4 * R ) ) = arccos ( ( 4 * 3750-2,75 ) / ( 4 * 3750 ) ) = 1,097147 ^o

L = 2 * R * tg ( γ / 2 ) = 2 * 3750 * tg ( 1,097147 / 2 ) = 71,81032 m

Lmin = max ( L^Ψ_min; Lⁿ_min ) = max ( 0,0214 * Vp^3 / ( R * Ψdop ) ; 0,7 * ( R ) ^ ( 0,5 ) ) = max ( 0,0214 * 120^3 / ( 3750 * 0,3 ) ; 0,7 * ( 3750 ) ^ ( 0,5 ) ) = max ( 32,8704; 42,8661 ) = 42,8661 m

L > L min

71,8103 > 42,87 warunek spełniony

yk = L^2 / ( 6 * R ) = 71,8103^2 / ( 6 * 3750 ) = 0,2292 m

n = yk-R ( 1-cos ( γ / 2 ) = 0,2292 - 3750 * ( 1-cos ( 1,097147 / 2 ) ) = 0,0573 m

Xs = L-R * sin ( γ / 2 ) = 71,810324 -3750 * sin ( 1,097147 / 2 ) = 35,9068 m

Ts = ( R + n ) * tg ( γ / 2 ) = ( 3750 + 0,057309 ) * tg ( 1,097147 / 2 ) = 35,9057 m

T₀ = Ts + Xs = 35,905711 + 35,906808 = 71,8125 m

Lc = 2 * T₀ * ( 1 + cos γ ) = 2 * 71,8125 * ( 1 + cos ( 1,097147 ) ) = 287,2237442199m

γⁱ₆ = arcsin ( p / 2 / To ) = arcsin ( 2,75 / 2 / 71,8125) = 1,097114 °

γ^{i + 1} = γⁱ₂ + ( γⁱ₆ + γⁱ₂ ) / 2 = 1,097147 + ( 1,097114 + 1,097147 ) / 2 = 1,097131 °

Druga iteracja

γ₂ = 1,097131 °

L = 2 * R * tg ( γ / 2 ) = 2 * 3750 * tg ( 0,019148 / 2 ) = 71,8092 m

Lmin = 42,87m

L > L min

71,8092 > 42,87 warunek spełniony

yk = L^2 / ( 6 * R ) = 71,8103 ^ 2 / ( 6 * 3750 ) = 0,2292m

n = yk-R ( 1-cos ( γ / 2 ) = 0,2292 - 3750 * ( 1-cos ( 1,097131 / 2 ) ) = 0,0573m

Xs = L-R * sin ( γ / 2 ) = 71,8092-3750 * sin ( 1,097131 / 2 ) = 35,9062591622m

Ts = ( R + n ) * tg ( γ / 2 ) = ( 3750 + 0,0573 ) * tg ( 1,097131 / 2 ) = 35,905162236m

T₀ = Ts + Xs = 35,905162236 + 35,9062591622 = 71,8114213982m

Lc = 2 * T₀ * ( 1 + cos γ ) = 2 * 71,8114213982 * ( 1 + cos ( 1,097131 ) ) = 287,219355543m

γⁱ₆ = arcsin ( p / 2 / To ) = arcsin ( 2,75 / 2 / 71,8114213982 ) = 0,0191485422 rad = 1,0971306505 °

γ^{i + 2} = γⁱ₂ + ( γⁱ₆ + γⁱ₂ ) / 2 = 1,097131 + ( 0,0191485422 + 1,097131 ) / 2 + = 1,0971 °

Trzecia iteracja

γ₂ = 1,0971 °

L = 2 * R * tg ( γ / 2 ) = 2 * 3750 * tg ( 1,097131 / 2 ) = 71,809227219m

Lmin = 42,87m

L > L min

71,809227219 > 42,87 warunek spełniony

yk = L^2 / ( 6 * R ) = 71,809227219^2 / ( 6 * 3750 ) = 0,2292 m

n = yk-R ( 1-cos ( γ / 2 ) = 0,2292 - 3750 * ( 1-cos ( 1,097131 / 2 ) ) = 0,0573 m

Xs = L-R * sin ( γ / 2 ) = 71,809227219-3750 * sin ( 1,097131 / 2 ) = 35,9062 m

Ts = ( R + n ) * tg ( γ / 2 ) = ( 3750 + 0,0573 ) * tg ( 1,097131 / 2 ) = 35,9052 m

T₀ = Ts + Xs = 35,9052 + 35,9062 = 71,8114 m

Lc = 2 * T₀ * ( 1 + cos γ ) = 2 * 71,8114 * ( 1 + cos ( 1,097131 ) ) = 287,2193 m

γⁱ₆ = arcsin ( p / 2 / To ) = arcsin ( 2,75 / 2 / 71,8114 ) = 1,0971 °

γ^{i + 2} = γⁱ₂ + ( γⁱ₆ + γⁱ₂ ) / 2 = 1,097131 + ( 1,097131 + 1,097131 ) / 2 = 1,0971 °

Po uzyskaniu żądanej dokładności kąt γ` = 1,0971 °

Z''' = Lc / p = 287,2193 / 2,75 = 104,4434

4. Wybór realizowanego wariantu

Optymalne poszerzenie spełnia zależność:

min ( Lc1 / p ; Lc3 / p ) = ( 98,0345 ; 104,4434 ) = 98,0345

Wybrano poszerzenie nr. 1.

2. Poszerzenie na wyjściu z łuku

Poszerzenie na łuku dla wariantu B

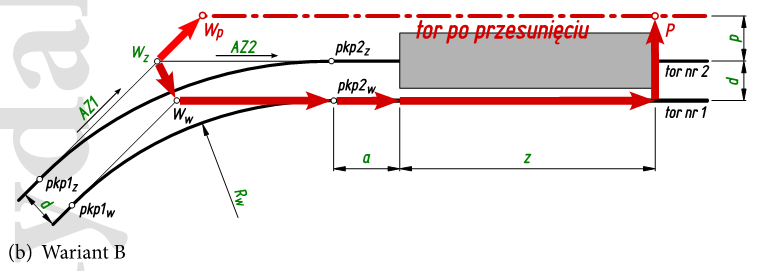
Parametry układu geometrycznego według rysunku:

Rw = 800,00 m

L = 110,00 m

a = 19,00 m

d = 4,50 m

z = 780,00 m

dmax = 7,25 m

Az1 = 71º

Az2 = 112º

Xwz = 3724,000 m

Ywz = 1198,000 m

γ = A_z2- A_z1 = 112 - 71 = 41 ⁰

1. Wartość przesunięcia wierzchołka głównego łuku

ΔW = |Wz-Wp| = p / sin ( γ ) = 4,5 / sin ( 0,715584993 ) = 4,1917

2. Azymut przesunięcia wierzchołka

Az1 = 71 ^o

3. Współrzędne punktów głównych

1. Wierzchołek przesuniętego łuku

Współrzędne przesuniętego wierzchołka toru zewnętrznego:

Xwp = Xwz + ΔW * cos ( Az2 + ( 180 - γ ) / 2 - 180 ) = 3724 + 4,1917 * cos ( 112 + ( 180 - 41 ) / 2 - 180 ) = 3725,3647 m

Ywp = Ywz + ΔW * sin ( Az2 + ( 180 - γ ) / 2 - 180 ) = 1198 + 4,1917 * sin ( 112 + ( 180 - 41 ) / 2 - 180 ) = 1201,9633 m

Wpółrzędne charakterystyczne dla toru zewnętrznego na łuku:

Dane

R = 804,5 m

L = 110,0 m

γ = A_z2- A_z1 = 112 - 71 = 41 ⁰

E = atan ( L / ( 2 * R ) ) = atan ( 100 / ( 2 * 804,5 ) ) = 3,9110 ^o

a = L - 2 * E = 11 - 2 * 3,9110 * 3,14 / 180 = 0,579067 rad = 33,1781 ^o

Xs = L - R * sin ( E ) = 110 - 804,5 * sin ( 3,9110 ) = 55,1281 m

yk = L ^ 2 / ( 6 * R ) = 110 ^ 2 / ( 6 * 804,5 ) = 2,506733 m

n = yk - R * ( 1 - cos ( E ) ) = 2,506733 - 804,5 * ( 1 - cos ( 3,910966 ) ) = 0,6332 m

Tkkp = L / ( 3 * cos ( E ) = 110 / ( 3 * cos ( 3,910966 )) = 36,7522 m

Tpkp = 2 * L / 3 = 2 * 110 / 3 = 73,3333 m

Ts = ( R + n ) * tg ( γ / 2 ) = ( 800 + 0,6332 ) * tg ( 41 / 2 ) = 301,0270 m

To = Ts + Xs = 301,0270 + 55,1281 = 356,1551 m

Xpkp1z = Xwz + To * cos ( Az1 + 180 ) = 3725,3647 + 356,1551 * cos ( 112 + 180 ) = 3609,4119 m

Ypkp1z = Ywz + To * sin ( Az1 + 180 ) = 1201,9633 + 356,1551 * sin ( 112 + 180 ) = 865,2121m

XM1 = Xpkp1z + Tpkp * cos ( Az1) = 3609,4119 + 73,3333 * cos ( 112) = 3633,2869 m

YM1 = Ypkp1z + Tpkp * sin ( Az1) = 865,2121 + 73,3333 * sin ( 112) = 934,5501 m

Xkkp1z = XM1 + Tkkp * cos( Az1 + m *E ) = 3633,2869 + 36,7522 * cos ( 71 + 1 * 3,910966 ) = 3642,8543 m

Ykkp1z = YM1 + Tkkp * sin( Az1 + m *E ) = 934,550123 + 36,7522 * sin ( 71 + 1 * 3,910966 ) = 970,0352 m

Xpkp2z = Xwz + To * cos ( Az2 ) = 3725,3647 + 356,1551 * cos ( 112 ) = 3599,7466 m

Ypkp2z = Ywz + To * sin ( Az2 ) = 1201,9633 + 356,1551 * sin ( 112 ) = 2227,1845 m

XM2= Xpkp2z + Tpkp * cos ( Az2 + 180 ) = 3599,7466 + 73,3333 * cos ( 112 + 180 ) = 3619,4178 m

YM2= Ypkp2z + Tpkp * sin ( Az2 + 180) = 2227,1845 + 73,3333 * sin ( 112 + 180 ) = 1464,1911 m

Xkkp2z = XM2 + Tkkp * cos( Az2 + m *E ) = 3619,4178 + 36,7522 * cos ( 112 +180 + 1 * 3,910966 ) = 3630,8292 m

Ykkp2z = YM2 + Tkkp * sin( Az2 + m *E ) = 1464,1911 + 36,7522 * sin ( 112 + 180 + 1 * 3,910966 ) = 1429,2553 m

2. Początek poszerzenia na prostej

Współrzędne wierzchołka toru wewnętrznego:

ΔZ = |WzwWww| = d / cos ( γ / 2 ) = 4,5 / cos ( 0,715584993 / 2 ) = 4,8042 m

Xww = Xwz + ΔZ * sin ( 90 - Az1 ) = 3724 + 4,1917 * sin ( 90 - 71 ) = 3719,1974 m

Yww = Ywz + ΔZ * cos ( 90 - Az1 ) = 1198 + 4,1917 * cos ( 90 - 71 ) = 1197,8742 m

E = atan ( L / ( 2 * R ) ) = atan ( 100 / ( 2 * 800 ) ) = 3,576334 ^o

a = L - 2 * E = 11 - 2 * 3,576334 * 3,14 / 180 = 33,134207 ^o

Xs = L - R * sin ( E ) = 110 - 800 * sin ( 3,576334 ) = 55,1295 m

yk = L ^ 2 / ( 6 * R ) = 110 ^ 2 / ( 6 * 800 ) = 2,5208 m

n = yk - R * ( 1 - cos ( E ) ) = 2,5208 - 800 * ( 1 - cos ( 3,576334 ) ) = 0,63688 m

Ts = ( R + n ) * tg ( γ / 2 ) = ( 800 + 0,63688 ) * tg ( 41 / 2 ) = 299,3459 m

To = Ts + Xs = 299,3459 + 55,1295 = 354,4754 m

Xpkp2w = Xww + To * cos ( Az2 ) = 3719,1974 + 354,4754 * cos ( 112 ) = 3586,4086 m

Ypkp2w = Yww + To * sin ( Az2 ) = 1197,8742 + 354,4754 * sin ( 112 ) = 1526,5380 m

XP'' = Xpkp2w + ( a + z ) * cos ( Az2 ) = 3586,4086 + ( 19,0 + 780,0 ) * cos ( 112 ) = 3287,0979 m

YP'' = Ypkp2w + ( a + z ) * cos ( Az2 ) = 1526,53801 + ( 19,0 + 780,0 ) * sin ( 112 ) = 2267,3580m

|P'' - P| = dmax = 7,25 m

ΔX = dmax * cos ( Az2 - 90 ) = 7,25 * cos ( 112 - 90 ) = 6,7221 m

ΔY = dmax * sin ( Az2 - 90 ) = 7,25 * sin ( 112 - 90 ) = 2,7159 m

Początek poszerzenia na prostej:

XP = XP'' - ΔX = 3287,0979 + 6,7221 = 3293,8200 m

YP = YP'' - ΔY = 2267,3580 + 2,7159 = 2270,0739 m

3. Początki i końce krzywych przejściowych i łuków

Parametry układu geometrycznego według rysunku:

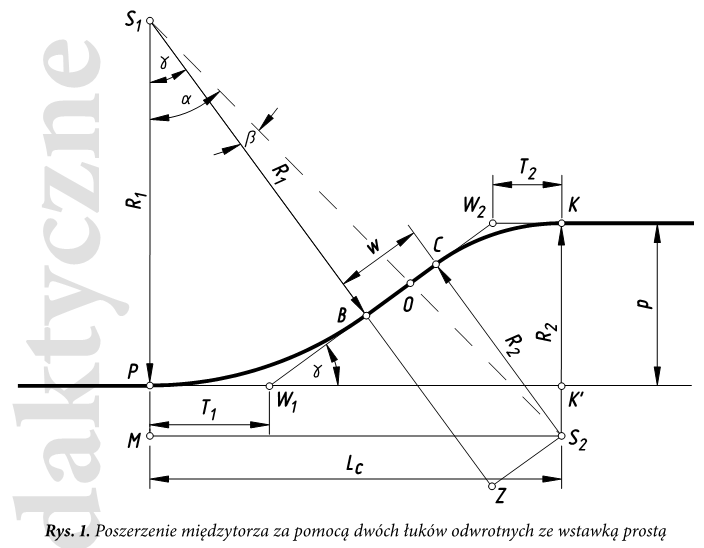
R 1 = R2 = 6200 m

γ = 0,936199 ^o

w = 67 m

Lc = 269,5949 m

T1 = T2 = 50,6543 m

XP = 3293,8200 m

YP = 2270,0739 m

|P - W1| = T1 = 50,6543 m

XW1 = XP + T1 * sin ( Az2 ) = XP + T1 * sin ( Az2 ) = 3293,8200 + 50,6543 * cos ( 112 ) = 3274,8445 m

YW1 = XP + T1 * cos ( Az2 ) = XP + T1 * cos ( Az2 ) = 3293,8200 + 50,6543 * sin ( 112 ) = 2317,0398 m

|W1 - B| = T1 = 50,6543 m

XB = XW1 + T1 * sin ( γ + Az2 - 90 ) = 3274,8445 + 50,6543 * sin ( 0,936199 + 112 - 90 ) = 3255,1042 m

YB = YW1 + T1 * cos ( γ + Az2 - 90 ) = 2317,0397 + 50,6543 * cos ( 0,936199 + 112 - 90 ) = 2363,6894 m

|B - C| = w = 67 m

XC = XB + w * sin ( γ + Az2 - 90 ) = 3255,1042 + sin ( 0,936199 + 112 - 90 ) = 3228,9939m

YC = YB + w * cos ( γ + Az2 - 90 ) = 2363,6894 + cos ( 0,936199 + 112 - 90 ) = 2425,3923 m

|C - W2| = T1 = 50,6543 m

XW2 = XC + T1 * sin ( γ + Az2 - 90 ) = 3228,9939 + 50,6543 * sin ( 0,936199 + 112 - 90 ) = 3209,2536 m

YW2 = YC + T1 * cos ( γ + Az2 - 90 ) = 425,3923201729600 + 50,6543 * sin ( 0,936199 + 112 - 90 ) = 2472,0419 m

|W2 - K| = T1 = 50,6543 m

XK = XW2 + T1 * sin ( γ + Az2 - 90 ) = 3209,2536 + 50,6543 * sin ( 0,936199 + 112 - 90 ) = 3190,2782 m

YK = YW2 + T1 * cos ( γ + Az2 - 90 ) = 2472,0419 + 50,6543 * sin ( 0,936199 + 112 - 90 ) = 2519,0078 m

PG WILIŚ

Bartłomiej Wiater sem VI Budownictwo indeks 132955 Obliczenia

9

---