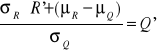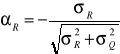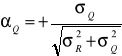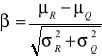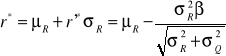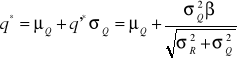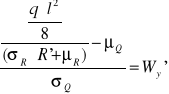Zadanie 4

Tabela 1. Parametry rozkładów prawdopodobieństwa do zadania 4a

Parametr	R	Q
mx	360	225
sx	36	27
Vx	0,10	0,12

Tabela 2. Parametry rozkładów prawdopodobieństwa do zadania 4b

R
mx	360
sx	36
Vx	0,10
mlnx	0,00995
s^2lnx	0,0998
slnx	5,88

Q
mx	225
sx	27
Vx	0,12
a	0,0475
u	213

Wykres 1. Zależność g = Q - R dla rozkładów normalnych

Z wykresu odczytano przecięcie prostej interpolującej z wartością 0 w punkcie -3,1

(dla 196 tyś próbek wyszło Pf = 0,00135 co odpowiada beta = 3)

b=3,1

Pf = 9,7 * 10^-4

Wykres 2. Zależność g = Q - R dla rozkładów innych niż normalne

Z wykresu odczytano przecięcie prostej interpolującej z wartością 0 w punkcie -2,7

(dla 196 tyś próbek wyszło Pf = 0,0032 co odpowiada beta = 2,73)

b=2,7

Pf = 3,5 * 10^-^3

Zadanie 5

Tabela 3. Parametry rozkładów prawdopodobieństwa do zadania 5

Parametr	R	Q
mx	360	225
sx	36	27
Vx	0,10	0,12

g(R,Q) = R - Q	Funkcja stanu granicznego
	Standaryzowana funkcja stanu granicznego
	Standaryzowane równanie stanu granicznego
	Standaryzowana zależność Q' od R'

	cosinusy kierunkowe prostej g'(R', Q') = 0 zwrócone w kierunku ujemnych wartości funkcji g'(R', Q')
	odległość prostej g'(R', Q')=0 od początku układu współrzędnych
	współrzędne punktu projektowego standaryzowanego
		współrzędne punktu projektowego

Tabela 4. Obliczone parametry

aR	-0,8
aQ	0,6
b	3,00
r'*	-2,4
q'*	1,8
r*	273,6
q*	273,6

Wykres 3. Funkcja stanu granicznego

Wykres 4. Standaryzowana funkcja stanu granicznego

Tabela 5. Porównanie wyników

	Zad 4	Zad 5
b	3,10	3,00
Pf	9,7*10^-4	1,0 * 10^-3

Wnioski

Wynik w zadaniu 5 jest wynikiem ścisłym, gdyż w przypadku liniowej funkcji stanu granicznego i rozkładów normalnych metoda ta jest metodą ścisłą.

Wynik z zadania 4 jest wynikiem przybliżonym, ale zachowuje dużą zbieżność z metodą ścisłą.

Zadanie 6

Tabela 6. Parametry rozkładów prawdopodobieństwa do zadania 6

Parametr	R [kN/m^2]	Wy [m^3]
mx	10 000	0,012
sx	1 500	0,00156
Vx	0,15	0,13

q = 20 kN/m

l = 4 m

kN m

	Funkcja stanu granicznego
	Standaryzowana funkcja stanu granicznego
	Standaryzowane równanie stanu granicznego
	Standaryzowana zależność Wy' od R'

Wykres 5. Funkcja stanu granicznego

Wykres 6. Standaryzowana funkcja stanu granicznego

Z wykresu wyznaczono

b=4,20

Pf = 1,33 * 10^-5

Tabela 7. Wyznaczone parametry

b	4,20
r'*	-4,2
w'*	-0,76
r*	3700
w*	0,0108

Zadanie 7

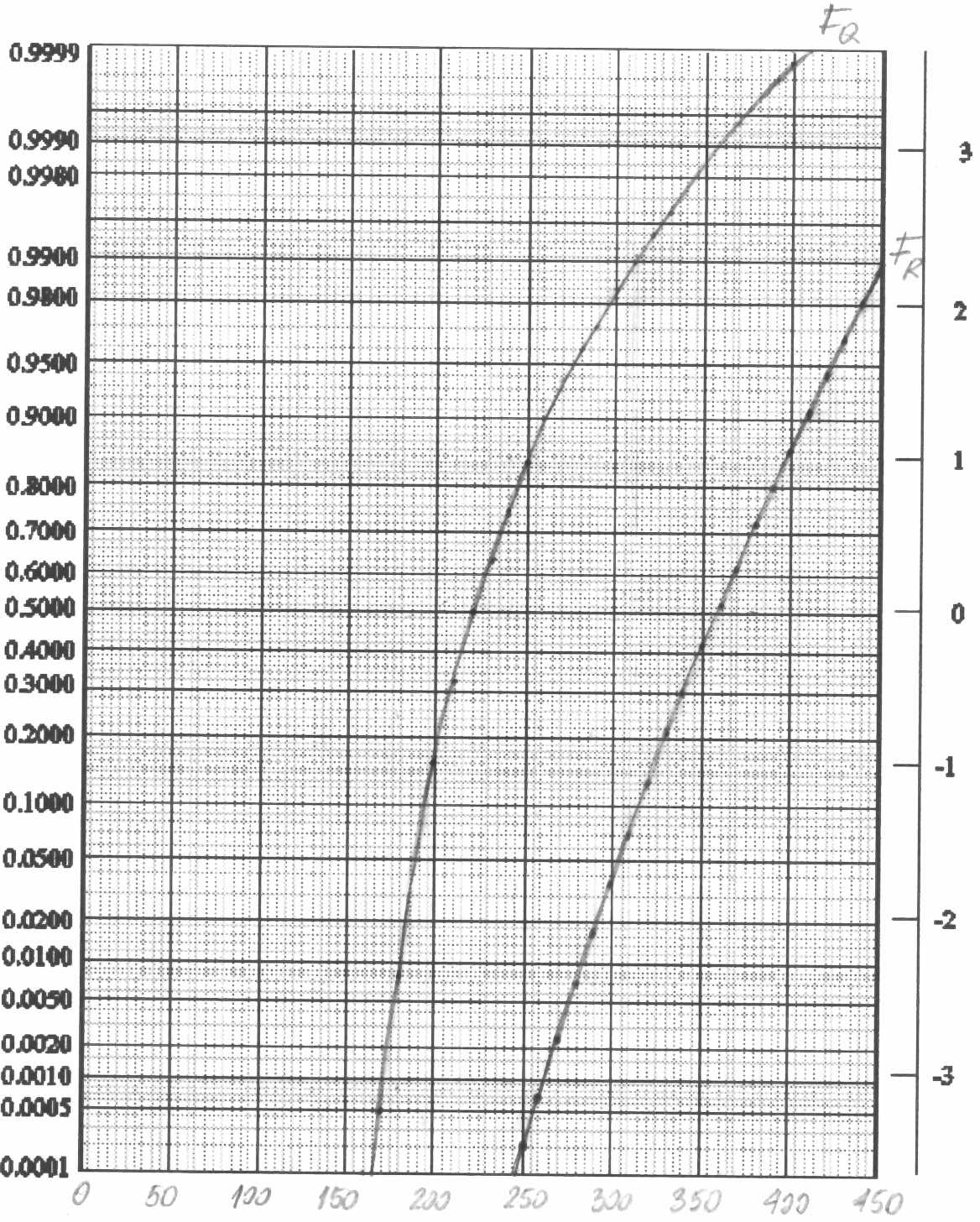
Tabela 8. Wyznaczone parametry zastępcze

Parametr	R	Q
mx	355	180
sx	35	55

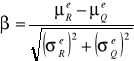
b=2,68

Pf = 3,68 *10^-3

Tabela 5. Porównanie wyników

	Zad 4b	Zad 7
b	2,70	2,68
Pf	3,50^-3	3,68 * 10^-3

Wniosek

Obie metody wykazują dużą zbieżność.

Krzysztof Ostrowski

Grupa KBI 1

- 9 -

---