FUNDAMENTOWANIE II (KB/TK) - ćw. projektowe w trzecim tygodniu

1. Wybór sprężystego modelu podłoża
   H - łączna grubość wszystkich warstw gruntowych pomiędzy poziomem posadowienia fundamentu a stropem skał zwięzłych, B - szerokość fundamentu

1. H < ~1,5B  Winkler

2. H > ~5,0B  półprzestrzeń sprężysta

3. ~1,5B < H < ~5,0B  warstwa sprężysta.

2. Wartości parametrów modelu podłoża. Założenia

• w projektowaniu parametry modelu wyraża się za pomocą tradycyjnych parametrów sprężystych
  E_o - moduł Younga (pierwotny), por. PN-81/B-03020  - współczynnik Poissona, por. PN-81/B-03020 (zwykle   0,3)
  Uwaga: dla półprzestrzeni sprężystej te dwa parametry występują jako (1-²)/E_o , dlatego często wprowadza się jeden moduł sztywności podłoża E_s, gdzie E_s = E_o/(1- ²),

• zakłada się, że osiadania fundamentu na podłożu modelowym są równe osiadaniom w_śr odpowiadającego ośrodka sprężystego o parametrach E_o,  ;   
  → daje to równanie do wyznaczenia parametrów sztywności podłoża modelowego,

• w najprostszym sposobie można wykorzystać wzór

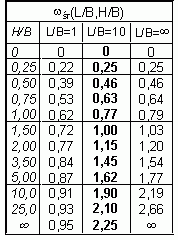
 w_śr1 = średnie osiadanie fundamentu BxL, równomiernie obciążonego q, na skutek ściśliwości warstwy sprężystej w zakresie głębokości 0 H    . Dla ław szeregowych najczęściej L/B ~ 10,

• Jeśli w zakresie głębokości 0 H są np. dwie różne warstwy o spągu kolejno z₁ oraz z₂ = H, to odpowiednio
  
  
  
  
  ... co łatwo uogólnić na w_śrn dla n > 2 warstw.

• Wartości parametrów modelu podłoża. Obliczenia

1. Model Winklera: tutaj w = q/C oraz z założenia w = w_śr1, stąd 1/C = B  _śr(L/B,H/B)/E_s, więc C = ...
   Odpowiednio należy brać w_śrn zamiast w_śr1, jeśli jest więcej warstw. Widać, że C jest funkcją B oraz L.

2. Półprzestrzeń sprężysta (przypadek ogólny n ≥ 1): odpowiednikiem uwarstwionej półprzestrzeni sprężystej o modułach E_si jest jednorodna półprzestrzeń sprężysta o zastępczym module
   , który znajduje się z następującego równania w_śr1(*) = w_śrn, tj. 
   
   
   
   
   gdzie z_o = 0 oraz z_n = H =  .

3. Warstwa sprężysta - w zasadzie postępuje się jak w b), ale dla H <  .

2. Przykład
   
   Według przyjętego założenia (p.2), dla ławy 2x20m, odpowiednikiem jednorodnej warstwy sprężystej o grubości H = 7m i module E_s = 25MPa jest półprzestrzeń sprężysta o module


.




¹ Tab.1.13 w skrypcie Fundamentowanie II. Przew.do projektowania. Tom II (W.Brząkała-red.), PWr., W-w 1990r. (alternatywnie można stosować współczynniki wz i wh wg Z.Wiłun, Zarys Geotechniki, WKŁ, W-wa 1982, str. 262)

---