LABOLATORIUM z Wytrzymałości Materiałów	Pałys Grzegorz
		Grupa: 32	Data: 13.01.2001
Temat: Wyznaczanie środka sił poprzecznych SSp.	Nr ćwiczenia: 6	Ocena:

1. TEORIA:

Belki wykonane z profili cienkościennych wykazują szereg własności zasadniczo odmiennych od odpowiednich własności spotykanych w belkach wykonanych z tzw. profili pełnych. Dla tej klasy profili niezwykle ważne okazuje się m.in. ustalenie poprawnego „prawidłowego” sposobu wprowadzenia siły poprzecznej. Punkt w płaszczyźnie przekroju, przez który powinna przechodzić ta siła integralna na ogół nie pokrywa się z środkiem ciężkości. Przyłożenie siły poprzecznej w niewłaściwym punkcie powoduje pojawienie się w belce, poza zginaniem dodatkowych jeszcze pól sił wewnętrznych m.in. skręcania, na które - szczególnie profile otwarte - są zazwyczaj mało wytrzymałe. Omawiany punkt nosi nazwę środka sił poprzecznych i stanowi „SSP” i stanowi ślad przebicia osi, wokół której następuje skręcenie belki z płaszczyzną jej przekroju.

Celem ćwiczenia jest doświadczalne wyznaczenie SSP oraz porównanie wyników pomiaru jego położenia z rezultatami obliczeń. Posłużymy się modelem belki ceowej, jednostronnie zamocowanej na całym obwodzie do podłoża, a drugim końcu - obciążonej siłą poprzeczną Q. Środek SSP wyznaczony z obliczeń - wypada poza konturem określonym przez wymiary gabarytowe przekroju. Niewłaściwe przyłożenie obciążeń poprzecznych do profili cienkościennych przy równoczesnym nie uwzględnieniu dodatkowo pojawiających się wówczas pól sił wewnętrznych może być przyczyną ich zniszczenia.

1. WYZNACZANIE ŚRODKA SIŁ POPRZECZNYCH W BELCE O PRZEKROJU CEOWYM.

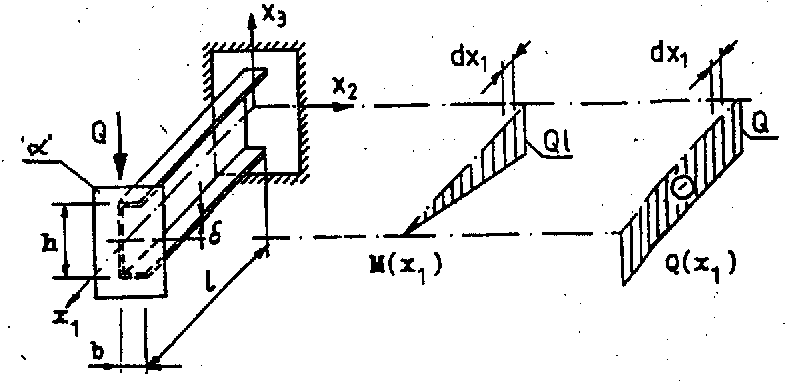
Rozważamy belkę wspornikową o długości l oraz wymiarach przekroju b, h,
.

Rozpatrywana belka jest obciążona siłą poprzeczną Q, którą wprowadzono za pomocą płaskiego elementu przepony
by przykładane obciążenie nie wywołało lokalnego zginania elementów składowych półek i środnika. Składowe pola naprężenia związane z momentem gnącym M(x) i siłą Q(x) w poszczególnych przekrojach x₁ mają rozkłady określone wzorami:

(1.1)

gdzie:

s - powierzchnia ceownika, współrzędna powierzchniowa,

moment statyczny odciętej części profilu względem x₂,

- grubość składowego elementu cienkościennego, w przekroju w którym odcina się wybrany fragment belki,

x_2, x₃ - osie główne, centralne przekroju,

J₂ - moment bezwładności względem x₂.

Dla odciętego przekrojem
otrzymamy warunek równowagi sił działających na x₁

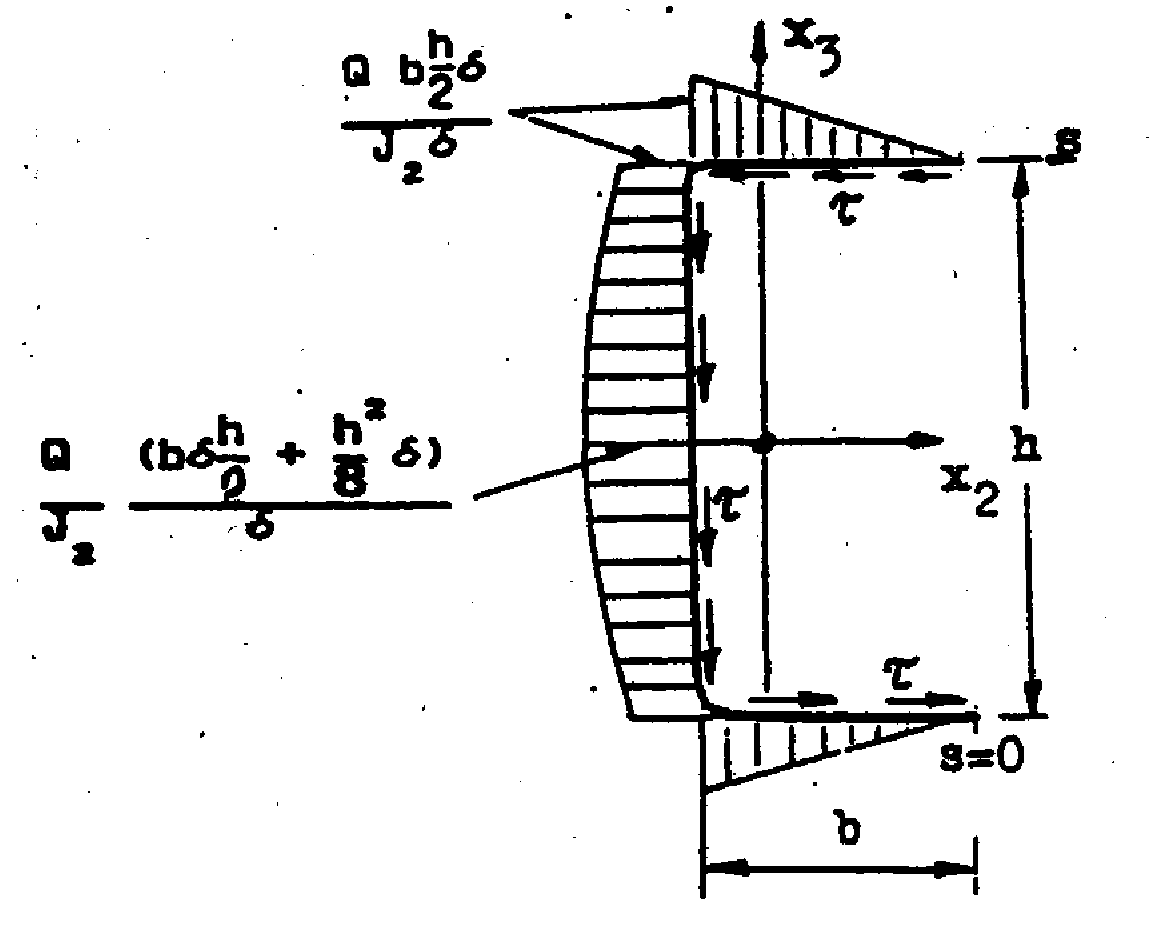
jest momentem statycznym części odciętej płaszczyzną
.

Wypadkowe oddziaływań naprężeniowych
w

półce górnej i dolnej wynoszą:

obciążając belkę siłą poprzeczną działającą w kierunku x₂ Q=Q₂ i wyznaczając SSP, dojdziemy do wniosku że siła Q=Q₂, tylko wtedy nie wywoła skręcenia profilu gdy będzie działała wzdłuż x₂. Tak więc SSP - jest to punkt przez który przechodzi wypadkowa oddziaływań stycznych
w konkretnym przekroju belki.

Redukując układ sił {T,TQ} np. do punktu A - otrzymamy siłę P_o= Q oraz moment

M_A = h T ,który jest prostopadły do P_o. Wypadkowa W tego układu sił ma zatem wartość W=Q i przechodzi przez punkt A` odległy od x

x

1. BUDOWA STANOWISKA:

• Belka ceowa, utwierdzona z jednej strony w podstawie, szalka z ciężarem jest mocowana do nakrętki, która może się przemieszczać w kierunku poziomym, gdy pokręcamy śrubą.

• Położenie ciężaru względem osi głównych profilu odczytujemy na podziałce `f' umieszczonej wzdłuż śruby.

• Do pomiaru kąta obrotu przepony służą dwa czujniki zegarowe.

przesunięcie	wskazanie L	wskazanie P
-40	4,7	5,06
-30	4,78	4,99
-20	4,87	4,74
-10	4,96	4,54
0	5,04	4,4
10	5,13	4,2
20	5,21	4,02

Wymiary badanego ceownika:

b=48 mm h= 90 mm g=1.5 mm Q=10.10 N

Moment bezwładności przekroju względem osi centralnej x₂:

J_x2=364305 [mm⁴]

Obliczenie teoretycznego położenia środka sił poprzecznych:

Korzystając ze wzoru na położenie środka sił poprzecznych:

Obliczam:

X_2Q =-19.21 mm

Z wykresu odczytujemy doświadczalny środek sił poprzecznych który wyniósł

X_2Q =-24 mm

Na wykresie naprężeń stycznych możemy zauważyć, że wypadkowe oddziaływań naprężeniowych τ≡σ_1s w półce górnej i dolnej są równe i wynoszą:

τ=Q*b*δ*0.5h/J_z*b*0.5=Q/J_z*b² *δ*h/4

Całkując podobnie oddziaływania styczne przyłożone do środnika otrzymujemy, że wartość ich wypadkowej jest równa Q.

WNIOSKI:

Doświadczalna metoda wyznaczania środka sił poprzecznych - SSP jest prosta i skuteczna pod warunkiem zachowania dokładności podczas wykonywania doświadczenia. Błędy powstałe podczas wykonywania pomiarów i późniejszych obliczeń powodują, że wyniki doświadczenia nie mają potwierdzenia w rzeczywistości. Ponadto zawsze będziemy obserwować różnice w położeniu środka sił poprzecznych wyznaczonym doświadczalnie i teoretycznie ze względu na wpływ wielu czynników, mających istotny wpływ na wynik doświadczenia. Jednak przy zachowaniu odpowiednich rygorów różnice te nie powinny być zbyt duże. Uzyskana w naszym doświadczeniu rozbieżność ok. 5 mm została zapewne spowodowana między innymi niezbyt dokładnym odczytaniem wskazań czujników pomiarowych.

Podczas ćwiczenia wyznaczaliśmy środek sil poprzecznych -SSP dla belki o profilu ceowym, obciążając ją siłą poprzeczną Q=10N i dokonując zmiany punktu przyłożenia siły od płaszczyzny środnika o odcinki równe od - 40[mm] do 20[mm]. Teoretycznie wyznaczona SSP wyniosła X_2Q =-19.21 mm, natomiast wyznaczona doświadczalnie X_2Q=-24 mm .Wyniki teoretyczny i doświadczalny różnią się w pewnym stopniu co świadczy o tym że doświadczenie zostało niezbyt poprawnie przeprowadzone. Rozbieżności pomiędzy wynikiem teoretycznym i doświadczalnym są spowodowane wieloma czynnikami. Błędami odczytu wskazań czujników, oraz błędami wprowadzonymi przez czujniki. Podczas wyznaczania teoretycznej wartości SSP założyliśmy ze mamy odczynienia z belka idealną i idealnie zamocowaną.

Aby naocznie przekonać się jak duży wpływ na sztywność i wytrzymałość konstrukcji wykonanych z profili cienkościennych ma sposób ich zamocowania, zaprezentowany został model z zamocowanymi w różny sposób profilami cienkościennymi oraz dwa modele ram samochodowych które przedstawiały jak mała zmiana warunków zamocowania wpływa na sztywność układu. Element zamocowany idealnie (tzn. wszystkimi krawędziami przekroju) do grubej stalowej płyty, posiadającej zdolność do przenoszenia sił normalnych, był zdecydowanie najbardziej odporny na obciążanie go jednocześnie momentem zginającym i skręcającym. W pozostałych przypadkach sztywność profilu była zdecydowanie mniejsza lub wręcz znikoma w przypadku profilu zamocowanego nie idealnie do cienkiej stalowej płytki. Przykład ramy samochodowej pozwolił nam zauważyć jak małe zmiany i wzmocnienia konstrukcji w punktach najbardziej przenoszących obciążenia pozwoliły na wielokrotne zwiększenie jej wytrzymałości na skręcanie oraz nośności. Z obserwacji wynika, że przy projektowaniu konstrukcji z profili cienkościennych zawsze należy dążyć do idealnego przypadku zarówno zamocowania jak i obciążania. Konstrukcje takie bowiem mają największe zdolności wytrzymałościowe. Jednak w praktyce sytuacje idealne spotyka się bardzo rzadko.

1

Laboratorium Wytrzymałości Materiałów Str- 3 -

---