Mechanika i wytrzymałość 06.03.2008r

Więzy i ich reakcje- jeżeli będziemy mieli jakieś ciało, które będzie opierało się o pow. jakiegoś innego ciała to w Puncie styku tych dwóch ciał, wystąpi reakcja, która będzie normalna oraz wystąpi tez pozioma reakcja t (siła pochodząca od tarcia), a wypadkowa… W momencie gdy będziemy rozpatrywać dwie gładkie powierzchnie to siła tarcia będzie dążyć do zera. Jeżeli pomijamy sile tarcia w tym przypadku, to traktujemy ciało jako, ciało idealne.

Ponadto mamy przegub walcowy, ciało osadzone jest w cylindrycznym sworzniu, przechodzący przez otwór wykonany w tym ciele. Jeżeli pominiemy tu siłę tarcia to reakcja tarcia na … i zawsze linia działania tej siły będzie przechodziła przez oś sworznia.

Przegub kulisty. Zakończenie pręta wykonane jest w kształcie kuli, która jest osadzona w kulistym łożysku. Jeżeli pominiemy siłę tarcia to reakcja będzie przechodziła przez środek kuli, która będzie zakończeniem tego pręta.

Podpora przesuwna. Reakcja w podporze będzie zawsze prostopadła do podłoża, czyli można powiedzie, że znamy kierunek działania wypadkowej.

Kierunek działania nie będzie prostopadły do podłoża. Będzie nachylony do podłoża pod jakimś kątem (tak jak na rys)

Składowe x, i y. Wartość reakcji uzyskujemy poprzez rozłożenie na składowe.

Jeżeli będziemy mieli przypadek, że wszystkie siły przyłożone do tej belki będą działały wzdłuż płaszczyzny przyłożonej do tej belki to wartość składowej poziomej będzie równa 0, dlatego że druga podpora jest przesuwna. Wartość reakcji przesuwnej będzie spadała do 0.

Gdy jest sama podpora a to musimy rozłoży na 2 składowe rax i Ray.

Płaski układ sił zbieżnych.

Mamy ciało, do którego zostały przyłożone ileś tam sił. Płaskim układem sił zbieżnych nazywa będziemy układ sił, których linie działania leżą w jednej płaszczyźnie i przecinają się w jednym punkcie. Ponieważ jak już wiemy siłę działającą na Ciało sztywne możemy przesuwać dowolnie wzdłuż linii jej działania. Siły zbieżne można zawsze traktować, jako siły przyłożone do jednego punktu.

Na rys. mamy do punktu, P mamy przyłożone 4 siły, p1, p2, p3, p4. Chcąc znaleźć wypadkową tych wszystkich sił, z boku w dowolnym miejscu zaczynamy przesuwa równolegle zaczynając od punktu p1, przenosimy kierunek i wartość tej siły. Następnie przykładamy kolejny wektor do końca siły p1 i podobnie z pozostałymi silami.

Można do też zrobić w ten sposób

Mamy siłę p1, p2, linią przerywaną otrzymujemy linii (wypadkową) otrzymujemy punkt C. Następnie równolegle od punktu C ciągniemy linie

Krótko mówiąc dowolny płaski układ sił, p1, p2, aż do pn przyłożonych do punktu O możemy zastąpi siłą wypadkową l równą sumie geometrycznej sił składowych i przyłożoną również w punkcie O.

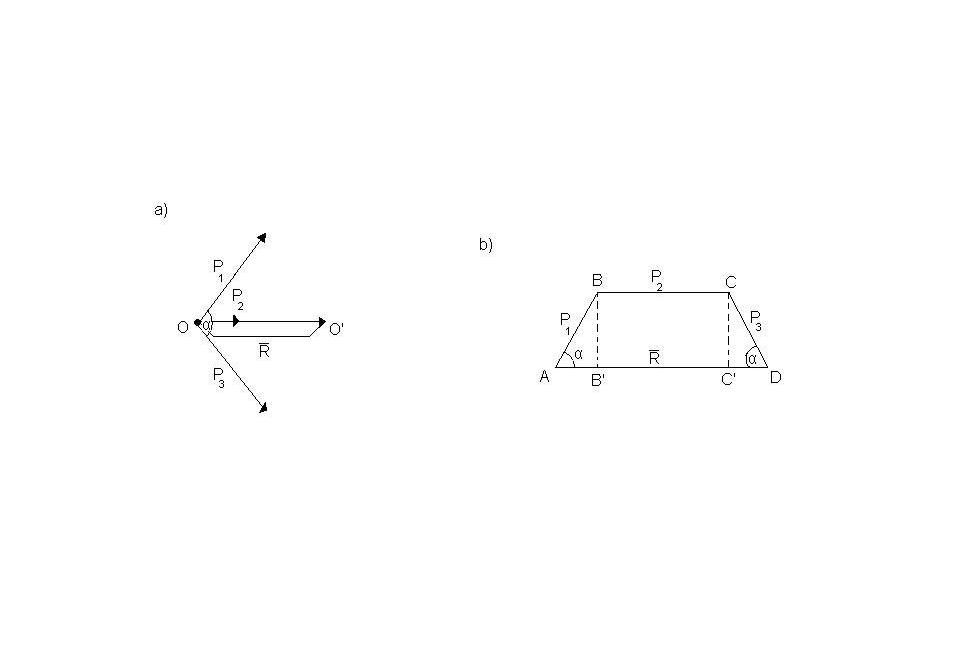
Przykład

Znaleźć wypadkową układu trzech sił p1, p2, p3 w przypadku, gdy wartości liczbowe tych sił są sobie równe. Czyli że p1=p2=p3=p. jeżeli wykonamy konstrukcje (jak na rys) to wartość liczbowa reakcji R równa się wartości odcinka AD = AB' +B'C'=C'D …

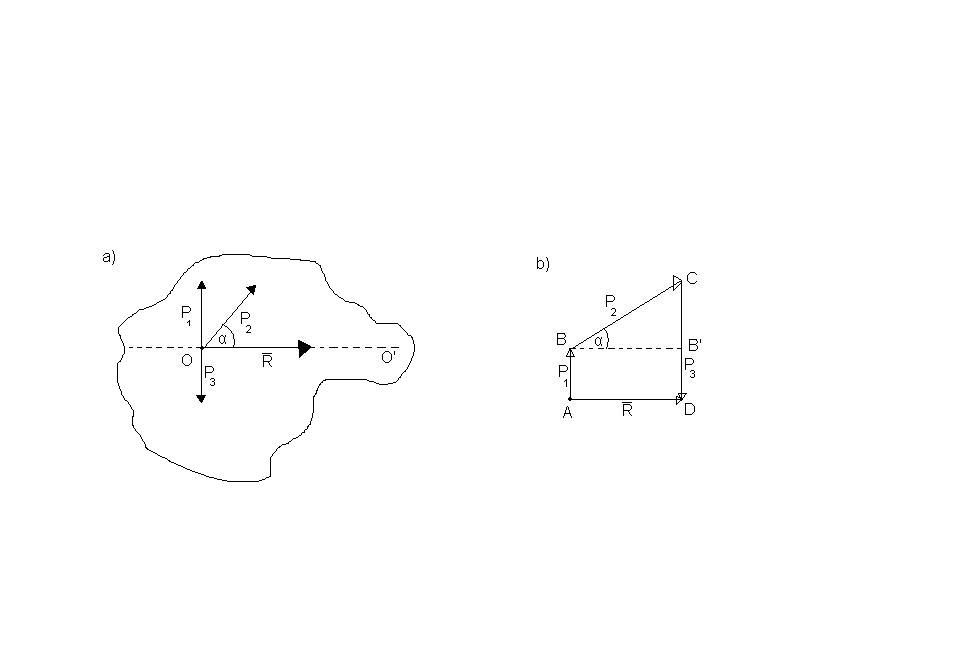
Do punktu O pewnego Ciała zostały przyłożone 3 siły. P1, p2, i p3 skierowane tak jak na rys. Określi mając dane wartości liczbowe p1, i p2, wartość siły p3, jeżeli wiadomo, że wypadkowa R ma być skierowana wzdłuż prostej oo'. P1= 10 N, p2=20N i kąt alfa=30 st.

Na rys mamy nakreślony wielobok sił, który w tym przypadku jest czworobokiem. Wypadkową R określa nam bok AD. Który zgodnie z tematem zadania musi by równoległy do prostej oo' Z rysunku otrzymamy, że p3=CD=CB'+B'D=p1+p2*sin alfa=20N Wartość liczbowa wypadkowej R=p2*cos alfa=10pierw3

Warunek równowagi płaskiego układu
sił zbieżnych.

Opierając się na sposobie znajdowania wypadkowej płaskiego układu sil zbieżnych, możemy wyprowadzi warunek, któremu muszą podlegać siły, aby ciało pod ich działaniem mogło pozostawać w równowadze. Równowaga możliwa jest oczywiście tylko w tedy, gdy wypadkowa tych sił jest równa). Czyli gdy wektory sił tworzą wielobok zamknięty. Oznacza to, że przy sumowaniu, koniec ostatniego wektora trafia na początek pierwszego.

Równowaga sił, taki układ sił pod działaniem, którego ciało będzie pozostawało w spoczynku ( będzie znajdowało się w równowadze). Reasumują, aby ciało pod działaniem sił zbieżnych, pozostawało w równowadze, wypadkowa musi by równa 0, co oznacza, że musi by utworzony wielobok zamknięty.

Jeżeli mamy tutaj układ 5 sił, z czego 3 siły są wiadome, co do wartości i kierunku a chcemy znaleźć wartość siły w i v.

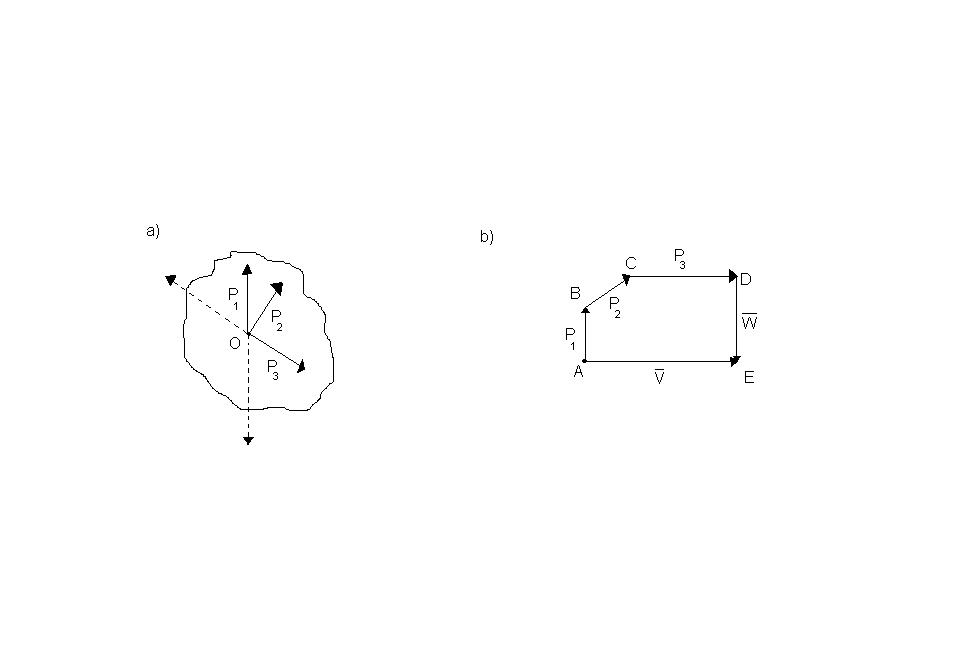
Z wykresu można odczytać wartości Vi W.

Przykład

Gładka jednorodna kula o ciężarze g, spoczywa na 2 gładkich płaszczyznach, nachylonych do poziomu pod kątami wynoszącymi 30 i 60 st. Należy wyznaczyć reakcje działające na kule w płaszczyznach styku z płaszczyznami.

Z rysunku można odczytać wartość reakcji w punkcie A i B

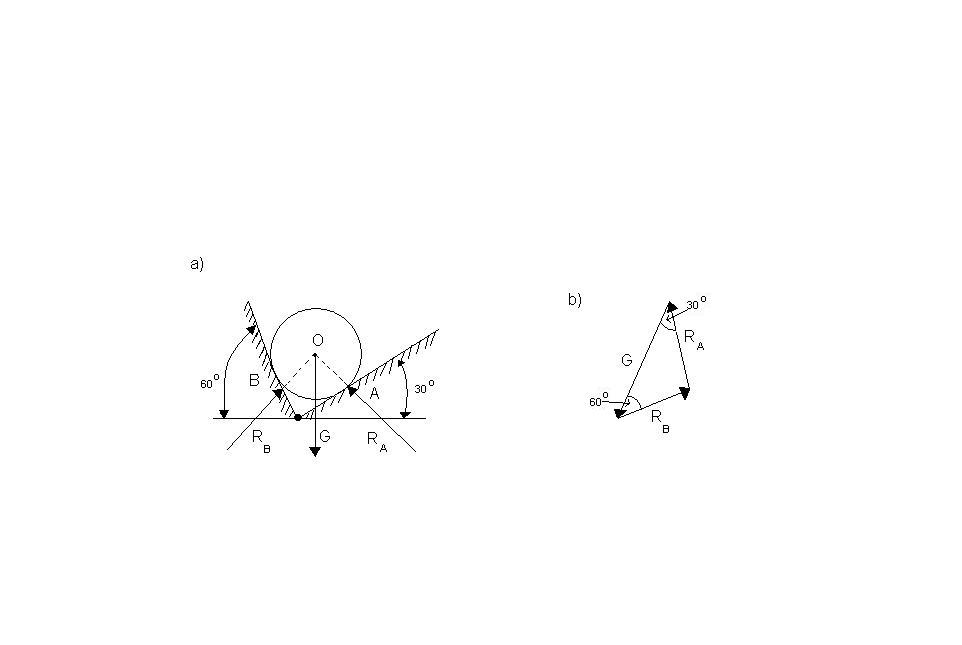
Mamy tutaj do czynienia z płaskim układem sił zbieżnych, że wartość Ra=G*cos30st, RB=G*sin60st

Przykład

Ciało o ciężarze g, zostało zawieszone na wiotkich nierozciągliwych i pozbawionych ciężaru cięgnach. Obliczyć napięcia cięgien.

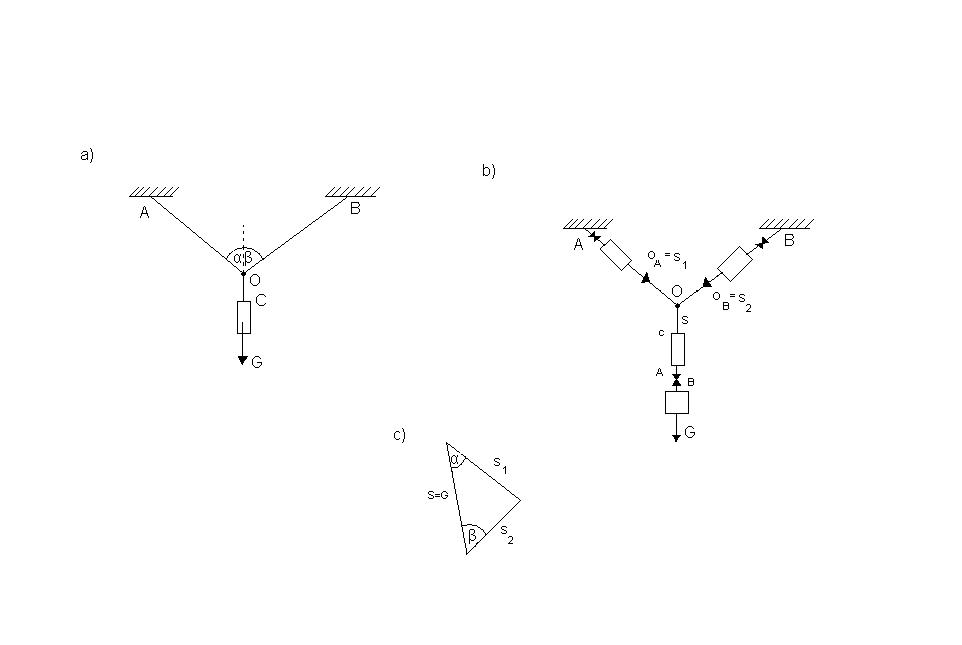
Mamy ciężar g, który został zawieszony na cięgnie O a, chcąc znaleźć reakcje znajdujące się na cięgnach, to możemy zrobić trójkąt sił.

Jeżeli weźmiemy pod uwagę reakcję cięgna, OC, której zaznaczono, jako S, to otrzymamy wartość tej siły będzie równa sile zawieszonego ciała S=G. Na punkt zaznaczony, jako O, działają 3 siły. Siła S oraz oddziaływanie cięgna OA oraz cięgna OB., Które zostały zaznaczone, jako S1 i S2, ażeby obliczy wartości tych siła, możemy zastosować, wzory sinusów, że S1/sin B=S2/sinalfa=g/sin[180-(alfa+B)] S1=G*sinB/sin(alfa+B) S2=G*sinalfa/sin(alfa+B

Przykład

Są tu przedstawione 2 pręty połączone ze sobą przegubowo w punkcie O, oraz w taki sam sposób przymocowane są do pionowej ściany. Na sworzniu w przegubie O zostało zawieszone ciało o ciężarze równym G. Należy określić siły działające na pręty. Wymiary na rys, Ciężary własne prętów oraz tarcie w przegubach należy pominąć.

Mamy 2 pręty połączone przegubowo w punkcie O i A, B. W punkcie A został zawieszony ciężar o wartości, G, jeżeli przyjmiemy odpowiednią skale możemy stworzyć trójkąt sił. Jeżeli popatrzymy na węzeł O to kierunek działania sił tak jak na rys. Pręt OA będzie rozciągany a pręt OB. Będzie ściskany.

Z podobieństwa trójkątów AOB i CDE otrzymamy, że S1

Natomiast z trójkąta prostokątnego OAB->OB.- pierwiastek kwadr+kwadr

Równowaga trzech sił nierównoległych. Mamy 3 siły, które są przyłożone do punktów A,B,C i zakładamy ze ciało to znajduje się w równowadze. Zakładamy, że linie działania tych sił leżą w jednej płaszczyźnie i nie SA do siebie równoległe. Linie działania siły p2, i p3 przecinają się w punkcie O. Siły te możemy przesunąć do punktu O i zastąpi te siły wypadową R' W rezultacie na ciało działają 2 siły R' i p1. Jeżeli dane ciało ma pozostawać w równowadze siły te muszą by równe, co do wartości liczbowych, przeciwnie, co do kierunku i działać wzdłuż jednej prostej. Wynika z tego, że linia działania siły p1 musi przechodzić też przez punkt O. Siły p1, p2 i p3 muszą tworzyć zamknięty trójkąt sił, co zostało przedstawione na rysunku.

Przykład

Pozioma belka AB połączona jest przegubowo końcem A z nieruchomą ścianą. Oraz zawieszona końcem B na cięgnie BD tworzącym kąt alfa z poziomą. Do belki została przyłożona pionowa siła P w odległości równej a od lewego końca. Należy znaleźć reakcję podpór. Długość belki jest równa l, ciężar własny belki pomijamy.

Z twierdzenia sinusów otrzymamy: (wzory na kartce)

Przykład

Gładki jednorodny pręt AB o długości 2l opiera się końcem A o gładką ścianę kanału, którego szerokość jest równa c. Po za tym pręt opiera się jeszcze o krawędź d tegoż kanału. Określić położenie równowagi przez podanie kata alfa, jaki pręt AB tworzy z poziomem.

Wiemy, że linie działanie wszystkich sił muszą przecinać się w jednym punkcie O. AO=AC*cos alfa=1*cos alfa. Z trójkąta ADO wynika… Jeżeli porównamy wyrażenia określające odcinki AO że l*cos alfa=a/cos kwadrat alfa… Czyli krótko mówiąc szerokość kanału może być mniejsza lub równa połowie długości pręta AB

Nie jestem pewien gdzie powinny być te wzoru, więc, wklejam je na koniec tego wykładu!!

Wykład 27 marca 2008

Znajdowanie wypadkowej płaskiego układu sił zbieżnych metodą rzutów na osie układów współrzędnych.

Równania równowagi.

Mamy jakąś siłę P, która została przyłożona do punktu O, z tego punktu możemy poprowadzić 2 wzajemnie prostopadłe osie współrzędnych Ox i Oy. Leżących w jednej płaszczyźnie z linią działania siły P. Jeżeli oznaczymy kąt alfa, jaka linia działania tej siły P tworzy z osią x to możemy napisać, że Px =P*cos alfa, oraz rzut na oś Y w Py=P*sin alfa może się zdarzyć, że będzie sytuacja odwrotna, że mamy dane Px, Py a będziemy musieli znaleźć wartość siły P, gdzie P= pierw Px2 + py2, a cos alfa=Px/P, sin alfa=Py/p. Z rys wektor OA, jest przekątną prostokąta OA' i OA” gdzie boki określają nam rzuty Px i Py. Wobec tego możemy uważać siłę P, jako wypadkową dwóch sił działających wzdłuż osi Ox i Oy. Możemy te siły zdefiniować, jako P1=i*PX, P2=i*Py wobec tego siła P=P1+P2.

Jeżeli sobie weźmiemy taki układ, że do jakiegoś punktu zostaną przyłożone siły P1, P2, P3, i p4, została znaleziona wypadkowa tych sił.

Wz.1

Natomiast tą wypadkową R można zrzutować, gdzie wartość Rx będzie równe wartości wszystkich sił zrzutowanych na oś X. Gdy będziemy znali rzuty wypadkowej na oś X i oś Y, możemy obliczyć kąt alfa, który tworzy linia działania wypadkowej R z osią X. R=pierw Px2+Py2, cos alfa = Px/R

Znaleźć wypadkową płaskiego układu sił zbieżnych P1, P2, P3, P4, gdy P1=1kN, P2=2kN, P3=1kN i P4=1kN, kąty, jakie tworzą siły z osią są na rys. P1x=P1*cos30=0,5pierw3, P2x=P2*cos60=1,0kN, P3x=P3*cos135=-0,5pierw2, P4x=P4*cos270=0., Ponieważ sin alfa, jaki cos są dodatnie wobec tego kąt alfa będzie w pierwszej ćwiartce, z tablic odczytujemy, że alfa wynosi59st7'

Powyższe równania są nazywane równaniami płaskiego układu sił zbieżnych.

Kula spoczywa na równi pochyłej, została ona zamocowana za pomocą cięgna OB., przy czym to cięgno tworzy z osią Ox kąt beta, kąt nachylenia równi jest zaznaczony, jako alfa

Jednorodna kula o Ciężarze G spoczywa na równi pochyłej nachylonej do poziomu pod kątem alfa, kula ta utrzymywana jest na równi przy pomocy cięgna AB, przywiązanego do stałego punktu B, obliczyć reakcję równi na kulę oraz napięcie Cięgna, pomijając ciężar tego ostatniego oraz tarcie pomiędzy powierzchnią kuli i równią. Należy zaznaczyć wszystkie siły występujące w temacie zadania. Ciężar G, napięcie cięgna S, reakcja równi C. wobec tego linia działania siły S na podstawie twierdzenia o trzech siłach musi również przechodzić przez ten punkt. Należy przyjąć układ współrzędnych jak na schemacie

, że oś OX jest równoległa do równi, a oś OY jest prostopadła do równi.

Mamy 2 ciała o ciężarze G i Q połączone przez przegub O i krążek C i połączone do punktu A, 2 ciała o ciężarach G i Q, zostały zawieszone na linach jak na rys. Przy czym lina OCB została przerzucona przez gładki kołek C. Znaleźć, jaka musi być zależność, między ciężarami G i Q, aby ciała pozostawały w równowadze. Zaznaczamy wszystkie siły występujące w temacie zadania. Należy rozpatrzyć równowagę węzła O. Na węzeł ten działają 3 siły, Q, G. Należy zrzutować te siły na oś OX. Wzory,

Znaleźć, jaką zależność muszą spełniać kąty alfa i beta, aby cięgno AB w położeniu równowagi zajmowało położenie poziome. Na podstawie zasady działania i oddziaływania Sa, Żeby położenie było w równowadze kąty

Wykład 10.04.08

Ciężar tego ciała spoczywającego na poziomej podłodze jest ozn. Literą G. Powierzchnie styku nie są gładkie(chropowate). Z doświadczeń wiemy, że dopóki wartość liczbowa siły P będzie odpowiednio niska to do pewnej granicy to ciał będzie znajdowało się w spoczynku. Będzie to ozn, że występuje siła T (występuje tarcie). Jeżeli zakładamy, że ciało znajduje się w równowadze to wartość siły T będzie równa P, wartość normalnej L będzie równa ciężarowi ciała. Jeżeli będziemy zwiększać wartość siły P to dojdziemy do takie pkt., w którym równowaga nie będzie możliwa. Z tego możemy wnioskować, że wielkość siły tarcia jest ograniczona. Nie możemy przekroczyć pewnej maksymalnej wartości. Prawa Tarcia: 1. Siła tarcia jest niezależna od wielkości stykających się ze sobą powierzchni i zależy jedynie od ich jakości. 2. Wielkość siły tarcia dla Ciała znajdującego się w spoczynku może się zmieniać od 0 do maksymalnej wartości proporcjonalnej do całkowitego nacisku normalnego N. 3. W Przypadku, gdy ciało ślizga się po pewnej powierzchni siła tarcia jest skierowana zawsze przeciwnie do kierunku . , ruchu, wielkość jej nie zależy od prędkości poślizgu. W przypadku, gdy siła tarcia jest mniejsza od maksymalnej wartości, jaką może ona osiągnąć, gdy nasze ciało jest w spoczynku. Na podstawie tych praw tarcia możemy ustalić zależności między siłą tarcia T i naciskiem normalnym. Dla ciała pozostającego w spoczynku na chropowatej powierzchnie T jest mniejsze bądź równe Ni. Ten współczynnik Ni, nosi nazwę współczynnika tarcia statycznego. Gdy siła tarcia osiąga swą maksymalną wartość, czyli mówimy, że tarcie jest rozwinięte. To w tedy piszemy, że T=Ni*n, gdzie T ozn. Graniczną siłę tarcia. Jeżeli chodzi o kierunek tej siły tarcia działającej na ciało znajdujące się spoczynku to siła ta jest przeciwnie skierowana do kierunku ruchu. W przypadku, gdy nasze ciało będzie ślizgało się po powierzchni chropowatej siła tarcia przeciwnie skierowana do kierunku ruchu, a jej wartość określamy Ni'*N, współczynnik Ni' nosi nazwę współczynnika tarcia kinetycznego.

Jeżeli zakładamy, że siła tarcia osiągnęła swą wartość graniczną, czyli T=Ni*N, że jeżeli przez Fi oznaczymy kąt, jaki tworzy wypadkowa R z normalną do powierzchni styku, to mamy, że T=N*tg Fi. Ponieważ rozpatrywanym przypadku, T i g = constans. kąt Fi jest maksymalnym kątem, o jaki może odchylić się linia działania wypadkowej reakcji R od kierunku normalnej do powierzchni styku. Kąt ten nazywamy kątem tarcia, czyli można napisać, że Ni=tg Fi, to jest współczynnik tarcia jest równy tg kąta tarcia. Jeżeli weźmiemy pewną normalną to ten kąt Fi będzie zakreślał pewien stożek, ze wypadkowa tutaj działająca, jeżeli będzie znajdowała się w tym stożku nie spowodował ruchu tego ciała, czyli jeżeli ozn sobie jakiś kąt alfa, to zależność, że alfa >= kątowi Fi.

Na równi pochyłej tworzącej z poziomem kąt alfa spoczywa ciało, o ciężarze G. Do ciała tego została przyłożona pozioma siła P, tak jak na rysunku. Znaleźć, w jakich granicach zmieniać się może wartość tej siły, jeżeli ciało pozostać ma w spoczynku. Współczynnik tarcia jest równy Mi.

Zaczniemy od przypadku, gdy siła p osiągnęła maksymalną wartość, przy której możliwa jest równowaga. Po przekroczeniu, której, ciało zaczęłoby się poruszać do góry, a więc w rozpatrywanym granicznym przypadku siła tarcia T osiąga swoją maksymalną wielkość i skierowana jest w dół tak jak na rys. B. Jeżeli obierzemy układ współrzędny jak na rys, otrzymamy następujące równania:

Jeżeli przejdziemy do przypadku, gdy siła T osiągnie swoją minimalną wartość, przy której jest możliwa równowaga, tj., że ciało nie zsuwa się po równi pochyłej tj. tak jak na ryc. C.

Na podstawie

Gdy jednak zwiększymy kąt nachylenia alfa, to ciało zacznie się od razu zsuwać.

Ciało o ciężarze G spoczywa na chropowatej poziomej podłodze. Należy określić, pod jakim kątem B do poziomu powinna być nachylona lina, za którą ciągnie się dane ciało, aby siła S potrzebna do wywołania poślizgu była najmniejsza. Kąt tarcia jest równy Fi. Jak zaznaczono na ciało działają siły: ciężar G, reakcja liny S, reakcja podłogi R. Jak wiemy linie działania tych trzech sił muszą przecinać się w jednym punkcie, czyli możemy zapisać, że:…

Równania3

Żeby siła powodowała poślizg S>

Aby poruszyć ciało przy użyciu najmniejszej siły linia winna tworzyć z poziomem kąt równy kątowi tarcia. Wówczas dla wywołania poślizgu musi być spełniony warunek, że B=sinFi

Pręt AB opiera się końcem A o poziomą podłogę zaś końcem B o pionową ścianę, przy czym oś pręta tworzy kąt alfa z poziomem. Katy tarcia między prętem i podłogą oraz ścianą są jednakowe i równe Fi. Obliczyć, w jakiej maksymalnej odległości x od końca A mierzonej wzdłuż osi pręta może być przyłożona do niego pionowa siła A, aby pręt pozostawał jeszcze w równowadze. Długość pręta AB równa jest l; jego ciężar…

Zadanie to rozwiązane za pomocą stożka tarcie zarówno dla pkt. A i B. Linie działania reakcji muszą leżeć wewnątrz tych obszarów. Z drugiej strony na pręt działają 3 siły: siła G oraz reakcje w punktach styku A i B. Równowaga tego pręta będzie możliwa wtedy, jeżeli linia działania tych sił będą przecinać się w jednym punkcie. Może to być spełnione jedynie wtedy, gdy linie działania pionowej siły G będzie przechodzić przez obszar zaznaczony na rysunku, jako obszar CDFE, jest to obszar dla obu stożków. Maksymalna wartość x, dla których równowagą będzie możliwa, otrzymamy z warunku, że linia działania siły G przechodzić będzie przez wierzchołek tego czworokąta zaznaczonego literą E. W tym przypadku linie działania obu reakcji odchylone będą od odpowiednich normalnych do powierzchni styku o kąt tarcia Fi. Z trójkąta prostokątnego ABE mamy, że BE =l*coslalfa +fi>r

Równanie 4a

Gdy linia działania siły G będzie przechodziła przez punkt E wtedy spełniona jest zależność:

Równanie 4b

Czyli aby równowaga była zachowana ta odległość x powinna być zawarta między 0 a tą wartością.

Moment siły względem punktu.

Niech będzie dana siła P jak na rys 5 Momentem siły względem punktu o zwanego biegunem będziemy nazywali iloczyn wartości liczbowej siły przez odległość jej linii działania od punktu O. Jeżeli ozn odległość, jako h, to moment siły względem punktu Mo=+-P*h. +- zależy od przyjętej umowy. Odległość h nazywamy ramieniem danej siły względem punktu O. Wartość momentu siły względem punktu nie zależy od tego, do jakiego punktu na linii działania przyłożona jest siła. Na rysunku mamy zakreskowany trójkąt OAB, którego pole Foab=1/2(AB)(OC)

Równania 5

Z powyższego wzoru wynika, że moment siły względem punktu jest liczbowo równy podwojonemu polu trójkąta. Moment może być równy, 0 jeżeli P lub h jest równe0. Jednostką momentu siły jest N(newton)*m(metr).

Równania 6

Długości odcinków OB.' I OC' są równe rzutom sił P1 i P2. Na podstawie twierdzenia o rzucie wektorów

Czyli moment wypadkowej jest równy sumie momentów wszystkich sił składowych i z tego jest twierdzenie Walignona że moment względem dowolnego punktu wypadkowej dwóch sił przyłożonych w jednym punkcie równy jest sumie algebraicznej momentów sił składowych względem punktu O. To powyższe stwierdzenie można uogólnić dla dowolnego płaskiego układu sił zbieżnych od P1 aż do Pn. Na podstawie tego twierdzenia możemy obliczyć moment siły P, gdy znane są współrzędne jej punktów przyłożenia w prostokątnym układzie OXY oraz rzuty sił na osie tego układu.

Mamy daną siłę P, która przyłożona jest do punktu A. Obliczymy moment tej siły względem początku układów. Jak wiemy siłę P można traktować, jako wypadkową 2 sił składowych Px i Py gdzie wypadkowa P=i*Px+j*Py. Obliczając moment siły Mo= Py *x-Px*y. Moment siły względem punktu jest równy 0 w dwóch przypadkach. A mianowicie, gdy siła jest równa 0 lub gdy linia działania przechodzi przez dany punkt.

Jeżeli będziemy mieli przyłożony do Punktu A układ sił, jeżeli suma momentów tych sił względem punktu B jest równa 0 to możemy wnioskować, że albo ich wypadkowa r jest równa 0 albo, że linia działania tej wypadkowej będzie przechodziła przez punkt, B. Gdy okaże się jeszcze, że suma momentów sił, względem innego punktu, np. C nielezącego na jednej prostej z punktami A i B jest także równa 0 to wówczas możemy stwierdzić, że wypadkowa R musi być równa 0.Aby ciało pod działaniem płaskiego układu sił zbieżnych pozostawało w równowadze, sumy momentów wszystkich sił względem dowolnych dwóch punktów nieleżących na jednej prostej z punktem przyłożenia sił winny równać się 0.

Mamy dwie siły o współrzędnych P1 i P2, które są przyłożone do punktu A o x=3m iy=1m, zakładając, że P1=1kN, obliczyć wartość liczbową siły P2 z warunku, że linia działania wypadkowej tych sił ma przechodzić przez początek układu współrzędnych. Na podstawie twierdzenia a rozpatrywanym naszym przypadku …

Równania 7

---