dr inż. Dominik Strzałka

Zakład Systemów Rozproszonych

Politechnika Rzeszowska

Wybrane zagadnienia z zakresu Elementów Logiki i Arytmetyki Komputerów

(wersja robocza - autor nie ponosi odpowiedzialności za ewentualne błędy w tekście)

Rzeszów 2009

Spis treści

Wprowadzenie

Jest rzeczą, z jednej strony dość zadziwiającą, a z drugiej dość oczywistą, że w ciągu ostatnich 20 lat systemy komputerowe stały się w naszym życiu wszechobecne. Początkowo informatykę kojarzono przede wszystkim jako pewną tajemniczą wiedzę, która sprawiała, że bezduszna maszyna z grubsza zbudowana z połączenia kilometrów ścieżek miedzianych i milionów tranzystorów staje się miłym i przyjemnym urządzeniem „figlarnie” mrugającym do nas z kolorowego ekranu. Urządzeniem, które potrafi zdziałać „cuda dziwy”, o ile tylko Pan informatyk potrafi wprawić je w „ruch”. W zasadzie w świadomości wielu osób nadal istnieje takie przekonanie, że informatykiem jest ten „co to zna się na komputerach”. Stwierdzenie to może budzić uśmiech, ale jeśli odnieść się do niego tak na spokojnie, to można powiedzieć, że jest w nim ukryty pewien głębszy sens, bo dziś informatyka nie jest tym „czymś”, czym była jeszcze naście lat temu.

Zauważmy, że jeszcze w latach 60 XX w. informatykę utożsamiano głównie z obliczeniami na liczbach podczas gdy dziś, informatyka jest raczej postrzegana jako przetwarzanie informacji w sensie operacji na tekście, strumieniu audio lub video, itp. Wydaje się jednak, że i ten etap powoli przechodził będzie do lamusa, bo czeka nas zupełnie nowa era, w której informatyka będzie utożsamiana z interakcją - jest to pewnego rodzaju metafora, w której informatyka rozumiana jako obliczenia traktowana będzie jako „coś, co się dzieje” w bliżej nieokreślonym środowisku. Tym środowiskiem będzie sieć (np. Internet); tak więc sieć będzie komputerem, ale i komputer będzie siecią. Brzmi to bardzo futurologicznie, ale czy ktoś w latach 70 XX w. myślał o Internecie ...

Nim jednak nastanie era futurologii należy opanować pewien elementarz, swoistego rodzaju fundament, bez którego jakakolwiek rozmowa o informatyce nie ma sensu. Niniejszy skrypt ma za zadanie w sposób jasny i przystępny pokazać tenże elementarz.

Reprezentacja stałopozycyjna liczb w systemie komputerowym. System binarny

Aby system komputerowy mógł dokonać jakichkolwiek użytecznych (bądź nie) obliczeń wymaganym jest, aby dostarczone mu dane miały dlań zrozumiałą reprezentację. Z jednej strony nie jest to sprawa prosta, bo czasem wymagane są pewne skomplikowane metody zakodowania danych, ale, z racji pewnych uwarunkowań natury fizycznej, znaleziono dość skuteczny sposób (choć rodzi się pytanie na ile efektywny) tegoż kodowania. Systemy komputerowe nadal w dużej mierze budowane są jako urządzenia bazujące na przepływie energii elektrycznej (bardziej ogólnie: pola elektromagnetycznego). Z tego też względu dość oczywistym stało się, że przechowywanie, przesyłanie i przetwarzanie danych zdecydowanie najwygodniej było oprzeć o system binarny często umownie reprezentowany jako „0” - „1”, który implementowany jest jako wysoki lub niski poziom napięcia elektrycznego. W systemie komputerowym jakiekolwiek dane (liczbowe, tekstowe, audio, video, etc.) reprezentowane są w postaci ciągów zer i jedynek, ale kwestią „umowy” (można by rzecz swoistego rodzaju protokołem) jest ich interpretacja. Zauważmy bowiem, że o ile w życiu codziennym posługujemy się olbrzymią ilością różnego typu znaków, o tyle system komputerowy musi ograniczyć się jedynie do dwóch umownych znaków-stanów: 0 lub 1, stan wysoki „H” lub niski „L”. Oczywiście tymi znakami-symbolami-stanami mogłyby być „a” i „b” lub „X” i „Y”, ale umowa zero-jedynkowa pozwala na sprowadzenie każdej reprezentowanej danej do postaci liczby. Można to potraktować jako pewną historyczna zaszłość, bowiem początki informatyki wiążą się ścisłe z matematyką a ta raczej kojarzy nam się z liczbami i pewnymi operacjami arytmetycznymi. Oczywiście jest to spore uproszczenie, ale nie wnikając dalej w szczegóły takich czy innych interpretacji przejdźmy do meritum problemu.

Jest faktem dość oczywistym, że każdego otaczają nas miliony różnego typu liczb. Dzięki pewnym historycznym uwarunkowaniom swego czasu uznaliśmy, że reprezentacja tychże liczb powinna opierać się o pozycyjny system dziesiętny. Choć jego powszechne użycie raczej nie przysparza nikomu wielkich problemów, to bardzo niewiele osób tak naprawdę zdaje sobie sprawę z tego, jak ten system funkcjonuje. Być może gdzieś tam, kiedyś w „zamierzchłych czasach” pokazywano nam w szkole jego istotę, ale na dzień dzisiejszy w zasadzie wiadomo tylko tyle, że system „działa”. Tymczasem jego idea ma pewien bardzo uniwersalny charakter, bowiem reprezentacja dowolnej liczby w pozycyjnym systemie dziesiętnym sprowadza się do jej zapisu w postaci dziesięciu (m.in. stąd system dziesiętny, ale nie tylko) umownych znaków (cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), które to umieszczone na odpowiednich pozycjach (stąd system pozycyjny) informują o wartości liczby. Kluczową rolę odgrywa tu także stwierdzenie, że system jest dziesiętny, bowiem każda reprezentowana w tym systemie liczba budowana jest jako suma cyfr przemnożonych przez wartości odpowiednich potęg liczby 10. Skąd bowiem wiadomo, że dla przykładu symbol 267 faktycznie oznacza dwieście sześćdziesiąt siedem jakiś tam „cudaków”. Otóż wiadomo, bo te 267 jest zbudowane jako suma liczb 2*100, 6*10 i 7. No ale skąd wiadomo, że 12,75 to właśnie dwanaście i siedemdziesiąt pięć setnych - wiadomo bo tym razem jest to suma liczb 1*10 + 2 + 7*0,1 + 5*0,01. Generalnie trzeba więc napisać, że w dziesiętnym systemie pozycyjnym każdą liczbę reprezentujemy jako:

gdzie a_i = 0,1,...,8,9.

Oczywiście sumy tej nigdy nie oblicza się od -∞ do +∞.

W przypadku systemów komputerowych dziesiętnym system jest raczej trudny do implementacji (wymagałoby to np. użycia dziesięciu wyraźnie rozróżnialnych poziomów napięć oraz układów elektronicznych potrafiących w ten sposób pracować) dlatego też oparto się o rozwiązanie najprostsze, czyli system dwójkowy inaczej zwany binarny. W systemie tym zamiast dziesięciu cyfr do dyspozycji pozostaje jedynie dwie: 0 i 1 a podstawą jest cyfra 2. Z tego też względu każda liczba jest reprezentowana jako:

gdzie a_i = 0,1.

No i sprawa w choć na pierwszy rzut oka jest prosta, to jednak zaczyna się powoli komplikować, bo trzeba znaleźć jakiś sposób na to, by móc liczby konwertować z jednego systemu na drugi. No i tymże sposobem teraz się zajmiemy.

Generalnie zasada jest dość prosta i w przypadku liczb całkowitych opiera się o operację dzielenia modulo przez 2 (tzw. dzielenia z resztą) i spisywania reszt aż do momentu, gdy część całkowita wyniesie 0. Spisywane reszty czyta się „od dołu do góry” wg załączonego poniżej przykładu:

Przykład 1

Dokonana zostanie konwersja liczby 27 na system binarny

27	: 2
Część całkowita	Reszta
13 6 3 1 0	1 1 0 1 1

Czyli 27₍₁₀₎ = 11011₍₂₎. Zauważmy specyficzny sposób notacji - oznaczenie w indeksie dolnym ₍₂₎ informuje, że jest t o system binarny, a oznaczenie ₍₁₀₎, że system dziesiętny.

A co z liczbami, które nie są całkowite. Dla części liczby „po przecinku” należy posłużyć się mnożeniem przez 2 jedynie części ułamkowej i spisywaniem części całkowitej aż do momenty gdy część ułamkowa wyniesie 0. Spisana część całkowitą czyta się „od góry do dołu”.

Przykład 2

Konwersja liczby 0,625 na system binarny

0,625	∙ 2
Część całkowita	Część ułamkowa
1 0 1	25 5 0

Czyli 0,625₍₁₀₎ = 0,101₍₂₎ (przykład znów był tendencyjny).

Zauważmy jednak, że nie każdy ułamek dziesiętny, która ma skończoną reprezentację w systemie dziesiętnym, daje się tak łatwo przedstawić w systemie binarny. Dla przykładu niech będzie to 0,1

Przykład 3

Konwersja liczby 0,1 na system binarny

0,1	∙ 2
Część całkowita	Część ułamkowa
0 0 0 1 1 0 0 1 1 0 0 1 ...	2 4 8 6 2 4 8 6 2 4 8 6 ...

Czyli 0,1₍₁₀₎ = 0,0001100110011...₍₂₎ i jak widać potrzeba nam nieskończonej liczby bitów by w systemie binarnym przedstawić liczbę 0,1₍₁₀₎. Oczywiście nietrudno zauważyć, że rodzi to pewne poważne konsekwencje, bo po pierwsze wiadomo, że liczba bitów jakimi dysponujemy w czasie wykonywania obliczeń (a i ogólnie rzecz ujmując w systemie komputerowym) jest ograniczona, tak więc nie można sobie pozwolić na użycie ich nieskończonej ilości, do superprecyzyjnej reprezentacji jakiejkolwiek liczby no a po drugie należy się zastanowić czy nie jest aby mitem, że komputery są tak precyzyjnymi maszynami. Oczywiście jest to w pewnym sensie „stawianie problemu na ostrzu noża” i ma on swoje pewne subtelne rozwiązania, ale nie czas i miejsce by o nim pisać.

Zaprezentowany powyżej sposób konwersji pokazuje jak liczbę dziesiętną zamienić na binarną. No ale „jak wrócić z powrotem”, czyli jak dokonać zamiany liczby z systemu binarnego na dziesiętny. Sprawa jest dość prozaiczna i wymaga zastosowania formuły , która dla liczby powstałej z połączenia Przykładu 2 i Przykładu 3 daje nam:

Przykład 4

Dokonać konwersji liczby 11011,101₍₂₎ na system dziesiętny

11011,101₍₂₎ = 1*2⁴+1*2³+0*2²+1*2¹+1*2⁰+1*2^-1+0*2^-2+1*2^-3 = 16 + 8 + 2 + 1 + 0,5 + 0,125 = 27,625₍₁₀₎.

Sposób konwersji przedstawiony w Przykładach 2, 3 i 4 ma bardziej ogólny charakter i można go wykorzystać do reprezentacji liczb nie tylko w systemie binarnym, ale i trójkowym, czwórkowym itd. Zmienia się tylko liczba, przez którą dokonywane jest dzielenie lub mnożenie oraz zmienia się podstawa systemu dla konwersji odwrotnej. Pewnym problemem stają się takie systemy liczbowe, w których liczba cyfr przekracza 10 (np. często używany w informatyce system szesnastkowy (heksadecymalny)), ale w takich systemach korzysta się z pomocy innych symboli, najczęściej są to litery. Dla przykładu w systemie szesnastkowym są to odpowiednio: A - cyfra 10, B - cyfra 11, C - cyfra 12, D - cyfra 13, E - cyfra 14, F - cyfra 15.

Oczywiście mimo iż konwersja ma dość prosty (niemal mechaniczny) charakter należy być ostrożnym, bowiem mogą czyhać na nas całkiem nieprzewidziane pułapki. Weźmy taki o to przykład:

Przykład 5

Ile to jest: A,A₍₁₆₎?

Jak widać mamy tu do czynienia z systemem szesnastkowym, więc A należy potraktować jako 10, ale A po przecinku nie oznacza 10 lecz oznacza 10∙12^-1 czyli jest to 10/12 zatem:

A,A₍₁₆₎ = 10,833333...₍₁₀₎

Przykład ten pokazuje nam także, że problem z Przykładu 3 może zostać odwrócony i liczba, która w innym systemie ma skończoną reprezentację „po przecinku” wymaga „okresu” w przypadku jej reprezentacji systemie dziesiętnym.

Temat reprezentacji danych w systemach komputerowych nie kończy się oczywiście na problemie konwersji liczb. Istnieje wiele ciekawych i interesujących kodów, bez których funkcjonowanie informatyki nie byłoby możliwe. W dalszej części materiałów kody te będą systematycznie przybliżane.

Reprezentacja zmiennopozycyjna liczb w systemach komputerowych. Standard IEEE 754/854

Truizmem będzie stwierdzenie, że żyjemy w świecie, w którym dostępne zasoby są ograniczone. Dotyczy to zarówno zawartości naszego portfela jak i ilości paliwa, które można wlać do baku samochodu (pomijając fakt na jaką ilość tego paliwa nas stać). Pewne ograniczenia mają charakter nie do końca od nas zależny, ale jest też tak, że wiele pomysłów człowieka realizowanych w rzeczywistości z założenia musi podlegać pewnym limitom, które są konsekwencją innych. Nie inaczej jest i z komputerami. W przypadku matematycznego pierwowzoru współczesnych komputerów, tzw. maszyny Turinga, nie było mowy o jakichkolwiek ograniczeniach, bowiem była to tylko (dla matematyków oczywiście aż) matematyczna idea, w której „sztandarowe” n→∞ raczej nikogo nie dziwi. Tymczasem realizacja jakiejkolwiek idei w świecie rzeczywistym wymaga zmierzenia się z prawami fizyki, które to zazwyczaj nakładają na nas niezliczoną liczbę ograniczeń. W przypadku systemów komputerowych jednym z najpoważniejszych problemów jest pojemność dostępnej pamięci. Słynne słowa szefa Microsoftu Billa Gatesa, który w 1981 roku oświadczył, że 640 kB pamięci powinno być wystarczające dla każdego brzmią dziś śmiesznie wszak 3GB pamięci w komputerze to nic specjalnego. Ale nie tylko pamięć i koszt jej wytworzenia jest tu problemem, bo zauważmy, że wykonanie jakiejkolwiek elementarnej operacji na ciągu bitów wymaga przepływu prądu elektrycznego poprzez różnego rodzaju układy scalone. Czy zawsze jesteśmy w stanie tak skonstruować architekturę tego układu by móc operować na ciągach bitów, które mają nieskończoną długość? Jest to pytanie retoryczne, bowiem w chwili obecnej w powszechnym użytku są architektury 32 lub 64 bitowe no a my marzymy o 256 lub więcej bitowych.

W związku z tym, że dostępna w danym momencie technologia i stan naszej wiedzy narzucają nam pewne ograniczenia zmuszeni jesteśmy do poszukiwań takich rozwiązań pewnych problemów, które pozwalają nam na „sprytne” ominięcie niektórych ograniczeń.

Weźmy oto taki przykład: w czasie pisania tekstu chcemy przekazać, że mamy do dyspozycji 1 milion $, czyli kwotę 1000000$. Lenistwo podpowiada nam, że zamiast pisać 7 cyfr możemy użyć tylko jednej i skrótu mln czyli 1 mln, co oczywiście jest dla nas zrozumiałe. Inżynierowie też często tak robią bo liczbę 1000000 mogą zapisać jak 1*10⁶ tzn. w postaci tzw. zapisu inżynierskiego. Jest to bardzo wygodne i pozwala dla przykładu liczbę 1500000 zapisać jako 1,5*10⁶. Co więcej w ten sposób można zapisać także liczbę 0,000001 jako 1*10^-6, itd. Cechą charakterystyczną tego zapisu jest fakt, że w zapisywanej liczbie przecinek „wędruje” w prawo lub lewo. Zdecydowanie lepiej widać to na przykładzie takich o to liczb: 234,56 = 2,3456*10² lub 0,845=8,45*10^-2. Swobodne przesuwanie przecinka nie zmienia rzeczywistej wartości liczby, ale w pewnym sensie pozwala na zaoszczędzenie miejsca użytego do reprezentacji liczby w postaci wykorzystanych znaków. Podobne rozwiązanie jest wykorzystywane w systemach komputerowych i zostało opisane za pomocą standardu IEEE754/854.

Generalnie liczby zmiennoprzecinkowe zapisuje się jako

gdzie: S - znak

M - mantysa

B - podstawa systemu

E - wykładnik

Mantysa powinna być znormalizowana tzn. należeć do przedziału <1, B-1> innymi słowy przed przecinkiem z lewej strony powinna znajdować się tylko jedna cyfra.

Standard IEEE 754

W systemach komputerowych operowanie arytmetyką zmiennopozycyjną wymaga zaimplementowania pewnych mechanizmów, które są wdrażane na bazie określonych standardów. Poniżej zajmiemy się jednym z nich a będzie to standard IEEE754 gdyż przedstawienie jego istoty jest kluczowe dla zrozumienia, jak funkcjonują inne tego typu rozwiązania. Jest to standard na tyle powszechny we współczesnych systemach komputerowych, że jego znajomość wydaje się być bardzo naturalna dla każdego, kto chce mienić się mianem informatyka.

Liczba w formacie IEEE-754 jest zapisywana za pomocą 32 bitów. Najstarszym bitem (tym najbardziej z lewej) jest bit znaku S (sign): dla liczby ujemnej S = 1, dla liczby dodatniej S = 0. Następnie w standardzie pojawia się 8 bitów kodujących wykładnik potęgi 2 (tzw. cecha), oraz 23 bity rozwinięcia binarnego (tzw. mantysa). W mantysie zawsze pomija się pierwszy niezerowy bit tzn. nie jest on wpisywany w standard. Ma to swoje pewne konsekwencje, ale o tym będzie później. Dzięki temu uzyskuje się 7-8 dziesiętnych miejsc znaczących i zakres reprezentowanych liczb od około ±1,18·10^-38 do około ±3,4·10³⁸.

S

E

E

E

E

E

E

E

E

M

M

M

M

...

M

M

M

M

1bit

8 bitów

23 bity

ZNAK

Wykładnik

Mantysa

Dodatkowo w standardzie IEEE 754 w przypadku wykładnika stosuje się pewien niezwykle ciekawy zabieg. Otóż zauważmy, że w przypadku wykładników także istnieje potrzeba reprezentacji liczb ujemnych i aby tu nie marnować bitu (w ten sposób ograniczając przecież zakres reprezentowanych liczb!) wprowadzone zostało tak zwane „obciążenie” i standardowo wykładnik jest równy 127₍₁₀₎ czyli 01111111₍₂₎, co oznacza, że za każdym razem kiedy zapisujemy w tym formacie jakąkolwiek liczbę musimy pamiętać, aby do wykładnika dodać/odjąć 127. Najlepiej będzie posłużyć się prostym przykładem. Zapiszemy w standardzie liczbę 118,625₍₁₀₎.

Przykład 6

Liczba 118,625₍₁₀₎ ma następującą postać binarną: 1110110,101₍₂₎.

1110110,101 = 1,110110101 ∙ 2⁶, co oznacza, że:

- mantysa powinna mieć postać: 11011010100000000000000;

- wykładnik: 6 + 127 = 133₍₁₀₎ = 10000101;

- znak: 0.

Zatem ostatecznie mamy: 0|10000101|11011010100000000000000.

Nie trudno zauważyć, że fakt, iż w standardzie pomija się pierwszą znaczącą jedynkę pozwala na poszerzenie zakresu zapisywanych liczb, ale z drugiej strony rodzi pewien poważny problem: skoro bowiem przecinek zawsze musi być przesunięty za pierwszą jedynkę, to jak w standardzie przedstawić 0 ??!! W zasadzie w tym standardzie nie jest to możliwe! Nie mniej jednak przyjęto, że gdy wykładnik jest równy 0 (tzn. w rzeczywistości ma on wartość dziesiętną -127, bo mamy 0 - 127 = -127) i wszystkie bity mantysą wynoszą 0, to taka liczba jest równa 0. No ale pozostaje jeszcze bit znaku, który może być równy 0 lub 1 i w tym drugim przypadku oznacza, że mamy do czynienia z tzw. zerem ujemnym. Temat ten nie będzie dalej poruszany, wystarczy mieć na uwadze, że są to dwie możliwe interpretacje 0 w przypadku standardu IEEE 754. Za nieskończoność uznaje się w standardzie wartość, w której wszystkie bity wykładnika ustawione są w 1, zaś mantysa równa jest 0. Gdyby w takim przypadku którykolwiek bit mantysy był równy 1 to taka liczba jest traktowana jako NaN (Not a Number) tzn. nie jest to liczba. Dotyczy to zarówno przypadku ze znakiem + jak i -. Zatem największa liczba jaką można przedstawić w standardzie wymaga ustawienia w 1 wszystkich bitów mantysy i ustawienia w 1 wszystkich bitów poza ostatnim (najmniej znaczącym bitem) w wykładniku. Zaś najmniejsza liczba wymaga wyzerowania wszystkich bitów w mantysie i ustawienia tylko jednego (najmniej znaczącego) bitu w wykładniku. To samo dotyczy się liczb ze znakiem -. Szczegóły można znaleźć w tabeli poniżej:

Liczba	Znak	Wykł.	Wykł. + 127	Wykł.	Mantysa	Wartość
Zero	0	-127	0	0000 0000	000 0000 0000 0000 0000 0000	0.0
Zero ujemne	1	-127	0	0000 0000	000 0000 0000 0000 0000 0000	-0.0
Jeden	0	0	127	0111 1111	000 0000 0000 0000 0000 0000	1.0
Minus jeden	1	0	127	0111 1111	000 0000 0000 0000 0000 0000	−1.0
Najmniejsza liczba	0 lub 1	-126	1	0000 0001	000 0000 0000 0000 0000 0000	±2^−126 ≈ ±1,18×10^-38
Największa liczba	0 lub 1	127	254	1111 1110	111 1111 1111 1111 1111 1111	±(2−2^−23) × 2^127 ≈ ±3,4×10^38
Nieskończoność	0	128	255	1111 1111	000 0000 0000 0000 0000 0000	+∞
„Nie liczba”	0 lub 1	128	255	1111 1111	nie zero	NaN

Podstawowe operacje arytmetyczne

Skoro jest nam znana zasada dokonywania konwersji pomiędzy systemami liczbowymi, warto przyjrzeć się kolejnym elementarnym operacjom jakie wykonywane są w systemie komputerowym. Będą to operacje arytmetyczne takie jak dodawanie, odejmowanie i mnożenie. Jak się na końcu tego rozdziału okaże wszystkie one sprowadzą się do tylko jednej, ale na razie niech tajemnicą pozostanie której.

Operacja dodawania wydaje się być stosunkowo najprostsza. Generalnie obowiązują tu zasady jakie znamy z klasycznych metod dodawania pisemnego w systemie dziesiętnym. Pamiętać jednak należy, że 1 + 1 = 0. Brzmi to dość kuriozalnie, ale wynika z faktu, że użycie cyfry 2 jest zabronione, więc faktycznie 1 + 1 = 0, ale pamiętać należy o przeniesieniu 1. Całość najlepiej sprawdzić na prostym przykładzie:

Przykład 7

Należy dodać: 1101₍₂₎ do 11001₍₂₎ (czyli 13 + 25 = 38)

Przeniesienie						Liczby
1	1	0	0	1
	1	1	0	0	1	25
		1	1	0	1	13
1	0	0	1	1	0	Suma = 38

Poczynając od prawej strony mamy kolejno:

1 + 1 = 0, przeniesienie 1;

1 + 0 + 0 = 1, przeniesienie 0;

0 + 0 + 1 = 1, przeniesienie 0;

0 + 1 + 1 = 0, przeniesienie 1;

1 + 1 + 0 = 0, przeniesienie 1;

1 + 0 + 0 = 1. STOP.

Wynik 100110₍₂₎ = 38₍₁₀₎.

Jak widać przy odrobinie wprawy dodawanie jest operacją niezwykle prostą i wykonywaną niemal intuicyjnie.

Również odejmowanie znane w klasycznej formie nie powinno przysparzać większych problemów. Oczywiście pamiętać należy, że 0 - 1 = 1 przy czym wynika to z faktu, iż z sąsiedniej pozycji (tej z lewej), pożyczamy 2. Zobaczmy przykład.

Przykład 8

Należy odjąć: 1101₍₂₎ od 11001₍₂₎ (czyli 25 - 13 = 12)

Pożyczka						Liczby
	0	2	2
	1	1	0	0	1	25
		1	1	0	1	13
	0	1	1	0	0	Różnica = 12

Poczynając od prawej strony mamy kolejno:

1 - 1 = 0;

0 - 0 = 0;

0 - 1 = 1, pożyczka z pozycji sąsiedniej = 2, wartość pozycja następnej = 0;

0 - 1 = 1, jako, że po wykonaniu operacji powyżej tu jest 0, pożyczka z pozycji sąsiedniej = 2, wartość pozycji następnej = 0;

STOP.

Wynik 1100₍₂₎ = 12₍₁₀₎.

Niemniej jednak ten sposób odejmowania jest dobry, gdy odjemna jest większa niż odjemnik. W sytuacji odwrotnej można zamienić miejscami odjemną z odjemnikiem pamiętając, że w wyniku końcowym należy dopisać znak minus `-`. Alu tu znów pojawia się kolejny problem. Jak w systemie komputerowym reprezentować ten minus. Czy użyć do tego jednego bitu? Ale przecież liczba dostępnych bitów jest ograniczona, może więc znak minus nie jest nam potrzebny.

Istnieje kilka rozwiązań tego problemu i w zasadzie każde z nich jest stosowane w systemach komputerowych. Reprezentacja znak ∙ moduł jest dla nas dość wygodna, ale nie do końca wygodna dla obliczeń w systemie komputerowym. Zauważmy, że x - y = x + - y tak więc klasyczne odejmowanie można zastąpić dodawaniem liczby przeciwnej tzn. równej co do modułu, ale ze znakiem -. Jak ten znak uzyskać? W sukurs przychodzą nam tzw. kody uzupełnieniowe i w przypadku systemu binarnego mamy do czynienia z kodem U1 (tzw. uzupełnienie do jedynki) oraz U2 (tzw. uzupełnienie do dwójki). Tworzenie kodu U1 jest banalnie proste: w liczbie należy wszędzie tam gdzie jest 0 wpisać 1, a tam gdzie 1 wpisać 0 (jest to tzw. negacja bitów). Kod U2 jest tworzony podobnie: najpierw należy zanegować wszystkie bity a potem dodać 1. Warto jednak zapamiętać, że liczby ujemne reprezentowane za pomocą kodów U1 lub U2 powinny zaczynać się od jedynek, to znaczy, że zanim dokonamy konwersji jakiejkolwiek liczby warto dopisać po jej lewej stronie przynajmniej jedno 0 - pamiętajmy, że ta operacja nie zmieni ich wartości.

Przykład 9

Liczba 11011 w kodzie U1 i U2 (w rzeczywistości liczbę te zapiszemy na 7 bitach, czyli 0011011)

0011011	Liczba
1100100	U1
1100100	U2
+ 1
1100101

Skoro wiemy, jak odejmować dodając, to powtórzmy Przykład 8 stosując naszą wiedzę.

Przykład 10

Należy odjąć: 1101₍₂₎ od 11001₍₂₎ wykorzystując kod U2

Liczba 1101 w kodzie U2 ma postać 10011, zatem

Przeniesienie						Liczby
1	0	0	1	1
	1	1	0	0	1	25
	1	0	0	1	1	- 13 w U2
1	0	1	1	0	0	Różnica =? 12

Jak widać wynik wynosi 101100₍₂₎ i nie jest to bynajmniej 12₍₁₀₎. Czyżby więc metoda nie działała? W przypadku kodów uzupełnieniowych i operacji dodawania należy pamiętać o tym, że: jeżeli decydujemy się na zapis z wykorzystaniem np. 5 bitów i w czasie wykonywania dodawania pojawi się przeniesienie na bit szósty, to bit ten pomijamy (nie występuje tzw. przepełnienie). Tak więc ostatecznie wynik wynosi 1100₍₂₎ czyli 12₍₁₀₎.

Prezentowany wyżej przykład był oczywiście prosty: od liczby większej odejmowaliśmy mniejszą, więc interpretacja wyniku nie nastręcza trudności. Co by było jednak gdyby sytuację odwrócić i dla przykładu odjąć od 13 liczbę 25, czyli wykonać 13 + -25.

Przykład 11

Należy odjąć: 11001₍₂₎ od 1101₍₂₎ wykorzystując kod U2

Liczba 11001 w kodzie U2 ma postać 100111, zatem

Przeniesienie						Liczby
0	1	1	1	1
0	0	1	1	0	1	13
1	0	0	1	1	1	- 25 w U2
1	1	0	1	0	0	Różnica = - 12(U2)

Jako wynik otrzymujemy liczbę 110100, która jest liczbą w kodzie U2. Jej moduł możemy wyznaczyć korzystając z metody z Przykładu 8, czyli negujemy wszystkie bity i dodajemy 1 otrzymując 1100₍₂₎ czyli 12₍₁₀₎.

Rozważmy teraz kolejną operację, jaką jest mnożenie. W systemie binarnym można posłużyć się dokładnie taką samą metodą jak w przypadku systemu dziesiętnego. Jako przykład wykonane zostanie mnożenie 5 ∙ 9 = 45 (czyli 101 ∙ 1001 = 101101)

Przykład 12

Należy pomnożyć: 101₍₂₎ przez 1001₍₂₎

Przeniesienie						Liczby
			1	0	1	5
		1	0	0	1	9
			1	0	1	Suma
		0	0	0
	0	0	0
1	0	1
1	0	1	1	0	1	45

Metoda jest bardzo prosta, ale posiada pewną słabą stronę. Zauważmy, że wymaga ona wykonania wielokrotnego dodawania. Oczywiście nie jest to dla komputera żadna trudność, ale każda z operacji dodawania zajmuje jakiś ułamek czasu i jeżeli mnożone przez siebie liczby są reprezentowane na dużej liczbie bitów, to cała operacja trwa dość długo. Istnieje jednak sposób, który w pewnych przypadkach pozwala na uniknięcie zbyt częstego dodawania. Określa się go mianem algorytmu Booth'a. Będzie on szczegółowo omówiony w innym miejscu.

Operacje arytmetyczne zmiennopozycyjne. Dodawanie, mnożenie algorytmem Booth'a

Zupełnie osobny problem stanowi kwestia wykonywania jakichkolwiek operacji arytmetycznych w jakimkolwiek standardzie zmiennopozycyjnym. Zauważmy, że w przypadku reprezentacji zmiennopozycyjnej elementarna operacja jaką jest dodawanie może być wykonać wtedy, gdy wykładniki obu liczb są takie same, co oznacza, że jeżeli mamy dwie liczby A i B, które mają odmienne wartości wykładników, to musimy tak przesunąć przecinek w jednej z tych liczb, aby zgadzały się wartości tychże wykładników. W wyniku tego jedna z liczb będzie nieznormalizowana. Po wykonaniu operacji arytmetycznej znów należy sprawdzić, czy liczba nie wymaga aby ponownej normalizacji. Doprowadzenie do tego, aby obie liczby miały taki sam wykładnik także jest rządzone pewną elementarną regułą: przesuwany jest przecinek zawsze u tej liczby, której wykładnik jest mniejszy tzn. w czasie wykonywania operacji dodawania obie liczby będą miały wykładnik taki, jaki jest przypisany liczbie z największą wartością. Jest to bowiem podyktowane tym, że jeżeli liczba ma mniejszą wartość, to w jej wypadku operacja przesuwania przecinka w lewo, prowadząca w niektórych przypadkach do tego, że najmniej znaczące bity zostaną utracone - czyli de facto zmieni się wartość tej liczby - będzie mniej szkodliwa niż utrata najbardziej znaczących bitów w liczbie większej. Zauważmy bowiem, że jeżeli z liczby 0,000000012₍₁₀₎ wyrzucimy ostatnią cyfrę, czyli 2, to będzie miało to mniejszy wpływ na wynik końcowy niż gdybyśmy z liczby 1223,23₍₁₀₎ usunęli pierwszą 1. W pierwszym przypadku tracimy bowiem jedynie dwie miliardowe, a w drugim cały tysiąc. Posłużmy się przykładem, w którym do liczby 13,625₍₁₀₎, czyli 1101,101₍₂₎ dodamy 3,75₍₁₀₎, czyli 11,11₍₂₎. Wynikiem powinno być: 17,375₍₁₀₎, czyli 10001,011₍₂₎.

Przykład 13

Należy dodać w standardzie IEEE 754 do liczby 13,625₍₁₀₎, czyli 1101,101₍₂₎ liczbę 3,75₍₁₀₎, czyli 11,11₍₂₎.

Liczba 13,625₍₁₀₎ zapisana w standardzie IEEE 754 ma postać:

0|10000010|10110100000000000000000

Zaś liczba 3,75₍₁₀₎ ma postać:

0|10000000|11100000000000000000000

W drugim składniku dodawania (jest to mniejsza liczba) musi zostać przesunięty przecinek w lewo o dwie pozycje zatem liczba ta będzie miała postać:

0|10000010|011110000000000000000000

Wykonujemy operację dodawania, ale tylko dla mantys:

	1	1	0	1	1	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	0	0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

W wyniku operacji dodawania otrzymujemy wynik: 10,001011, co oznacza, że nie jest on znormalizowany, tzn. przecinek nie znajduje się tuż za pierwszą jedynką, dlatego też należy przesunąć go o kolejną pozycję w lewo pamiętając by do wykładnika w standardzie dodać 1 (o tyle pozycji bowiem przesunięty został przecinek!). Ostatecznie więc wynik ma postać:

0|10000011|000101100000000000000000

Dla operacji odejmowania, pamiętając o tym, że jest ono realizowane jako dodawanie liczby w kodzie U2, postępujemy podobnie.

Nieco inaczej postępuje się w przypadku mnożenia. Wtedy problem przesuwania przecinka przed przystąpieniem do obliczeń nie jest konieczny. Najpierw mnoży się obie liczby, potem dodaje ich nieobciążone wykładniki (czyli w IEEE 754 są to wykładniki z odjętą wartością 127) a na końcu, jeżeli jest to konieczne, ponownie normalizuje uzyskany iloczyn. Jako przykład ilustrujący ideę posłuży nam mnożenie liczb z Przykładu 13.

Przykład 14

Należy pomnożyć w standardzie IEEE 754 do liczby 13,625₍₁₀₎, czyli 1101,101₍₂₎ liczbę 3,75₍₁₀₎, czyli 11,11₍₂₎.

Liczba 13,625₍₁₀₎ zapisana w standardzie IEEE754 ma postać:

0|10000010|10110100000000000000000

Zaś liczba 3,75₍₁₀₎ ma postać:

0|10000000|11100000000000000000000

W wyniku mnożenia mantys otrzymujemy, że 13,625₍₁₀₎ ∙ 3,75₍₁₀₎ = 51,09375, czyli 110011,00011₍₂₎. W zapisie zmiennopozycyjnym będzie to 1,101101 ∙ 2³ ∙ 1,111 ∙ 2¹ = 1,101101 ∙ 1,111 ∙ 2³⁺¹. Mnożenie możemy wykonać klasyczną metodą (ta była prezentowana w przykładzie) ale tym razem posłużmy się metodą opartą o algorytm Booth'a przy założeniu, że liczby będą reprezentowane na ośmiu bitach.

Podczas mnożenia algorytmem Booth'a mamy do dyspozycji mnożną P i mnożnik Q. Operacja wykonywana jest bit po bicie i polega na cyklicznym (tylu krotnym, ile bitów liczą mnożone liczby) sprawdzaniu dwóch ostatnich bitów mnożnika Q po to, by w zależności od ich wartości wykonywać operacje: dodaj do wyniku pośredniego +P, jeżeli porównane bity są w konfiguracji 01; dodaj -P jeżeli porównane bity są w konfiguracji 10; dodaj do wyniku pośredniego 0 (inaczej: nie rób nic) jeżeli bity są w konfiguracji 11 lub 00 a następnie należy wykonać tzw. operację przesunięcia bitowego w prawo (często oznaczaną jako SHR lub Shift Right). Cały algorytm postępowania wydaje się być dość tajemniczy, dlatego najlepiej zobrazować jego istotę działania na przykładzie (najpierw mnożone liczby będą inne niż w przykładzie 14).

Przykład 15

Pomnożymy za pomocą Algorytmu Booth'a dwie liczby: P = 10₍₁₀₎ 01010₍₂₎ ∙ Q = 5₍₁₀₎ 00101₍₂₎

Wynikiem powinno być 50₍₁₀₎ 0000110010₍₂₎

P = 01010

-P(U2) = 10110

KROK		A						B					C		Operacja
1		0	0	0	0	0		0	0	1	0	1	0		- P
		1	0	1	1	0		0	0	1	0	1	0		ADD
		1	0	1	1	0		0	0	1	0	1	0		SHR
2		1	1	0	1	1		0	0	0	1	0	1		+ P
		0	1	0	1	0		0	0	0	1	0	1		ADD
	1	0	0	1	0	1		0	0	0	1	0	1		SHR
3		0	0	0	1	0		1	0	0	0	1	0		- P
		1	0	1	1	0		1	0	0	0	1	0		ADD
		1	1	0	0	0		1	0	0	0	1	0		SHR
4		1	1	1	0	0		0	1	0	0	0	1		+ P
		0	1	0	1	0		0	1	0	0	0	1		ADD
	1	0	0	1	1	0		0	1	0	0	0	1		SHR
5		0	0	0	1	1		0	0	1	0	0	0		SHR
		0	0	0	0	1		1	0	0	1	0	0		STOP
		W Y N I K

Operacja ADD oznacza, że wykonujemy dodawanie.

W kolumnie A przechowywany jest wynik pośredni kolejnych kroków algorytmu, zaś w kolumnie B w pierwszym kroku wpisana jest liczba Q. Pierwsze porównanie bitów zawsze odbywa się z bitem 0 (kolumna C). Operacja SHR wykonywana jest w ten sposób, że jeżeli najbardziej znaczący bit (ten z lewej) równy jest 0, to po przesunięciu w prawo bit ten także jest równy 0, jeżeli zaś jest on równy 1, to po przesunięciu w prawo nadal wynosi 1. Jak widać wykonanych jest tyle operacji SHR ilu bitowe są liczby a w prezentowanym przykładzie wykonano tylko 4 dodawania (4 x ADD). Jak łatwo zauważyć algorytm ten zdecydowanie zmniejsza liczbę wykonywanych dodawań, jeżeli w mnożniku występują długie ciągi zer lub jedynek.

Operacja mnożenia jest wykonywana na liczbach 5-o bitowych zatem ostatecznie wynik jest odczytywany z dziesięciu bitów w po ostatnie operacji SHR. Generalnie jeżeli mnożenie zostało wykonane na n bitach to wynik jest 2n bitowy.

Teraz wróćmy do naszego analizowanego Przykładu 14 i pomnożymy przez siebie dwie zmiennopozycyjne liczby.

P =		0	1	1	0	1	1	0	1
-P =		1	0	0	1	0	0	1	0
-PU2 =		1	0	0	1	0	0	1	1
		0	0	0	0	0	0	0	0		0	0	0	0	1	1	1	1	0	-P
		1	0	0	1	0	0	1	1		0	0	0	0	1	1	1	1	0	ADD
		1	0	0	1	0	0	1	1		0	0	0	0	1	1	1	1	0	SHR
		1	1	0	0	1	0	0	1		1	0	0	0	0	1	1	1	1	SHR
		1	1	1	0	0	1	0	0		1	1	0	0	0	0	1	1	1	SHR
		1	1	1	1	0	0	1	0		0	1	1	0	0	0	0	1	1	SHR
		1	1	1	1	1	0	0	1		0	0	1	1	0	0	0	0	1	+P
		0	1	1	0	1	1	0	1											ADD
	1	0	1	1	0	0	1	1	0		0	0	1	1	0	0	0	0	1	SHR
		0	0	1	1	0	0	1	1		0	0	0	1	1	0	0	0	0	SHR
		0	0	0	1	1	0	0	1		1	0	0	0	1	1	0	0	0	SHR
		0	0	0	0	1	1	0	0		1	1	0	0	0	1	1	0	0	SHR
		0	0	0	0	0	1	1	0		0	1	1	0	0	0	1	1	0	STOP

W związku z tym, że w pierwszej liczbie po przecinku było 6 bitów znaczących, a w drugiej 3, w wynik mnożenia przecinek znajdzie się na dziewiątej pozycji licząc od prawej więc jest w postaci 11,001100011, co oznacza, że potrzebna będzie jego normalizacja. Nim jednak będzie ona dokonana pamiętajmy o obliczeniu mantysy, która w analizowanym przykładzie będzie wynosiła: 3 + 1 = 4 (o trzy pozycje w lewo przesunięty był przecinek dla pierwszej liczby i o jedną pozycję w lewo dla liczby drugiej). Ale pamiętając o normalizacji (musimy przesunąć przecinek o jeszcze jedną pozycję w lewo) ostatecznie iloczyn ma postać:

0|10000100|100110001100000000000000

czyli 1,1001100011 ∙ 2^132-127 = 1,1001100011 ∙ 2⁵ = 51,09375₍₁₀₎.

Jak widać arytmetyka zmiennopozycyjna, choć niezwykle pomysłowa w swojej idei, jest dość skomplikowana do zrealizowania w praktyce. Dlatego też w dzisiejszych procesorach znajdują się specjalne bloki funkcjonalne, których głównym zadaniem jest realizowanie właśnie takich obliczeń. Nie bez znaczenia pozostaje tu także problem dokładności obliczeń, dlatego też istnieją standardy np. IEEE 854 gdzie do dyspozycji jest 64 bity, tak by uzyskać możliwie jak największą precyzję obliczeń. Mogłoby się wydawać, że maszyny takie jak komputery są wprost stworzone do wykonywania różnego typu obliczeń matematycznych, ale skończona liczba dostępnych bitów pamięci oraz pewne uwarunkowania związane z ich architekturą wprowadzają istotne ograniczenia i w wielu przypadkach należy posługiwać się zupełnie innymi rozwiązaniami programowymi, by móc wykonywać super dokładne obliczenia.

W tym miejscu należy zwrócić także uwagę na fakt, że matematyka to nie tylko dodawanie, ale także np. logarytmowanie, pierwiastkowanie, podnoszenie do różnych potęg. Jak tu radzi sobie komputer. Oczywiście korzysta z reprezentacji zmiennopozycyjnej i do wykonywania tego typu obliczeń wykorzystywane są tzw. rozwinięcia w szereg lub pewne algorytmy umożliwiające obliczanie wyżej wymienionych operacji. Oznacza to, że w komputerze tego typu operacje sprowadzane są do operacji elementarnych (w zasadzie tylko do jednej jaką jest dodawanie!). Nawet stałe matematyczne takie jak e i π nie są na stałe zapisane w pamięci komputera tylko obliczane z ich rozwinięć w szeregi. Jeżeli jednak tak się dzieje, to wynika z tego, że wykonywanie wszelkiego typu operacji zmiennopozycyjnych jest bardzo czasochłonne. Z tego też względu istnieje pewna miara tzw. MFLOPSy (Millions Floating Point Operations Per Second) jako miara wyrażająca tempo wykonywania tego typu obliczeń w procesorze w jednostce czasu. Kiedyś zajmował się tym oddzielny koprocesor matematyczny, dziś tego typu układ jest wbudowany w strukturę jednostki centralnej.

Elementy logiki. Algebra Boole'a

Kolejny temat, który zostanie omówiony w tym opracowaniu to tzw. algebra Boole'a. Definicja matematyczna algebry Boole'a mówi nam, że jest to: „co najmniej dwuelementowy zbiór zamknięty ze względu na dwa działania dwuargumentowe, jedno działanie jednoargumentowe i dwa działania zeroargumentowe, taki że dla jego wszystkich elementów spełniony jest określony zespół aksjomatów”. Jak widać z opisu nie za wiele wynika, dlatego też w dalszej części tekstu pod nazwą algebra Boole'a należy rozumieć zero-jedynkową algebrę sygnałów binarnych z logicznymi operacjami sumy (OR, LUB, +), iloczynu (AND, I, ∙), negacji (NOT, NIE, ¯), określonymi tak, jak w tabeli poniżej oraz zbiór następujących (dziesięciu) aksjomatów dla tej algebry:

1). x + x = x, x ∙ x = x, idempotentność

2). x + y = y + x, x ∙ y = y ∙ x, przemienność

3). x + (y + z) = (x + y) + z, x ∙ (y ∙ z) = (x ∙ y) ∙ z łączność

4). x + (y ∙ z) = (x + y) ∙ (x + z), x ∙ (y + z) = (x ∙ y) + (x ∙ z) rozdzielność

5). x + (x ∙ y) = x, x ∙ (x + y) = x pochłanianie

6). x + 0 = x, x ∙ 1 = x własności stałych

7). x + 1 = 1, x ∙ 0 = 0

8). x + x = 1, x ∙ x = 0 własność negacji

9). x = x podwójna negacja

10). x + y = x ∙ y, x ∙ y = x + y prawa de Morgana

Nadto w algebrze tej spełniane są następujące właściwości:

0 = 1

1 = 0

1 + 1 = 1

1 ∙ 1 = 1

1 + 0 = 0 + 1 = 1

1 ∙ 0 = 0 ∙ 1 = 0

Operacje +, ∙, ¯ są operatorami znanymi z logiki matematycznej, które są definiowane jako:

x	y	x + y	x ∙ y	x	y
0	0	0	0	1	1
0	1	1	0	1	0
1	0	1	0	0	1
1	1	1	1	0	0

Na bazie tych operacji istnieje możliwość zbudowania innych operatorów takich jak negacja sumy NOR, negacja Iloczynu NAND oraz operator nierównoważności EX-OR oraz jego negacja EX-NOR (operator równoważności). Szczególnie ważnym operatorem jest EX-OR (symbol ⊕) - czasem jest on zdefiniowany jako suma modulo 2. Operacja EX-OR jest zdefiniowana jako: x ⊕ y = x ∙ y + x ∙ y i zwraca logiczną prawdę, gdy tylko i wyłącznie jeden z argumentów jest prawdziwy.

UWAGA: w dalszej części opracowania, ze względu na pewne ograniczenia użytego edytora zostanie przyjęte, że oznaczeniem symbolu logicznej negacji będzie ` (tzw. prim) zamiast symbolu ¯.

Funkcje EX-OR i EX-NOR są swoim wzajemnym zaprzeczeniem.

Przykład

(A⊕B)'=(AB'+A'B)'=(AB')' ∙ (A'B)'=(A'+B'') ∙ (A''+B')=A'A+A'B'+BA+BB'=A'B'+AB=A⊗B

oraz

(A⊗B)'=(A'B'+AB)'=(A'B')' ∙ (AB)'=(A''+B'') ∙ (A'+B')=AA'+AB'+BA'+BB'=AB'+A'B=A⊕B

Dzięki istnieniu dziesięciu w/w aksjomatów algebry istnieje możliwość upraszczania wyrażeń logicznych oraz wykonywania pewnych logicznych operacji, które czasem mogą wydawać się bardzo „karkołomne”. Rozważmy kilka takich przykładów.

Przykład

Udowodnić, że: (ABC')'+(ABC')=1

Zauważmy, że możemy zapisać, iż ABC'=X wtedy powyższe wyrażenie ma postać: X'+X=1 a na mocy aksjomatu 8 jest to prawda.

Przykład

Udowodnić, że: A + A'B = A + B

Lewą stronę wyrażenie możemy zapisać następująco:

A + A'B = A∙1 + A'B = A∙(B'+B) + A'B = AB' + AB + A'B = AB' + AB + AB + A'B = A(B'+B) + B(A'+A) =
A∙1 + B∙1 = A+B

I jak widać lewa strona równa się prawej.

W zasadzie stosowanie aksjomatów algebry Boole'a jest dowolne i celem nadrzędnym tej operacji jest możliwie jak największe upraszczanie formuł logicznych. Czasem jednak upraszczanie zastępuje się „utrudnianiem”. Brzmi to dość dziwacznie, ale istnieje w logice pojęcie tzw. systemu funkcjonalnie pełnego. Jest to taki zestaw podstawowych operacji logicznych, który umożliwia przedstawienie wszystkich innych operacji, jakie są używane w algebrze Boole'a. Takim systemem funkcjonalnie pełnym jest trójka operacji +, ∙, ¯, ale także na mocy praw de Morgana można zauważyć, że wystarczy kombinacja +, ¯ lub ∙, ¯ , by również uzyskać system funkcjonalnie pełny. Istnieją dwie funkcje, zaprzeczenie sumy (NOR) i zaprzeczenie iloczynu (NAND), które także stanowią właśnie taki system funkcjonalnie pełny. Są to operacje min. dwuargumentowe i aby udowodnić, że stanowią one taki system zauważmy, że dla zanegowanej sumy (NOR):

A' = (A+A)'

A+B = ((A+B)' )' lub ((A+B)' + (A+B)')'

A∙B = (A+A) ∙ (B+B) = (((A+A) ∙ (B+B))')' = ((A+A)' + (B+B)')'

zaś dla zanegowanego iloczynu (NAND)

A' = (A∙A)'

A∙B = ((A∙B)' ∙ (A∙B)')'

A+B = A∙A + B∙B = ((A∙A + B∙B)')' = ((A∙A)' ∙ (B∙B)')'

Oczywiście należy zadać sobie pytanie: a czemu to stosuje się tak zawiłe operacje i „utrudnia sobie życie” najpierw upraszczając pewne wyrażenia logiczne, a następnie je tak rozbudowuje. Odpowiedź jest dość prosta i wynika z pewnych uwarunkowań natury technologicznej. Otóż w elektronice cyfrowej każda taka operacja jest realizowana za pomocą funktora logicznego (tzw. bramki), która jest niczym innym jak układem scalonym zbudowanym z połączenia tranzystorów i rezystorów. Wewnętrzną budowę każdej z bramek logicznych cechują pewne charakterystyczne cechy a także uwarunkowania natury fizycznej np. problem możliwości fizycznego łączenia pewnych typów bramek. Okazuje się, że jeżeli wszystkie bramki uda się wykonać w jednej technologii albo (co jest jeszcze lepsze) wszystkie funkcje logiczne będą możliwe do zaimplementowana za pomocą bramki jednego rodzaju (typu) w/w problemy można zdecydowanie łatwiej rozwiązać.

Funkcje i funktory logiczne

Podstawowym elementem umożliwiającym praktyczne zastosowanie kwestii wynikających z algebry Boole'a jest możliwość posiadania odpowiednich funktorów logicznych, które będą realizowały podstawowe funkcje logiczne takie jak: suma OR (LUB), iloczyn AND (I), negacja NOT (NIE), ale także funkcje bardziej rozbudowane np.: EX-OR, EX-NOR, NAND, NOR. W technice cyfrowej posługujemy się wtedy tzw. bramkami logicznymi (często mówi się krócej: bramkami), za pomocą których budowane są schematy układów logicznych. Bramki posiadają swoje symbole, których kształt jest opisany za pomocą standardu ANSI. Co prawda istnieją inne standardy opisujące kształt bramek logicznych (w Polsce także taki standard funkcjonuje), ale w większości książek powszechnie stosuje się symbole, które będą zaprezentowane poniżej.

Łącząc wyżej zaprezentowane funktory logiczne można zbudować sprzętową implementację dowolnej funkcji logicznej zapisanej za pomocą algebry Boole'a. Generalnie przyjmuje się, że bramki logiczne mogą posiadać dowolną liczę wejść, ale nic nie stoi na przeszkodzie by narzucić na etapie rysowania schematu połączeń z góry określoną liczbę takich wejść, np. wszystkie bramki będą miały nie więcej niż 3 wejścia, co może oznaczać nieco większe skomplikowanie układu.

Niżej przedstawione zostaną różne warianty realizacji funkcji logicznych za pomocą funktorów.

A⊕B = AB'+A'B

A⊗B = A'B'+AB

A + A'B

(A+A)'

A+B = ((A+B)' )' lub ((A+B)' + (A+B)')'

A∙B = (A+A) ∙ (B+B) = (((A+A) ∙ (B+B))')' = ((A+A)' + (B+B)')'

A' = (A∙A)'

A∙B = ((A∙B)' ∙ (A∙B)')'

A+B = A∙A + B∙B = ((A∙A + B∙B)')' = ((A∙A)' ∙ (B∙B)')'

Zauważmy, że projektowanie jakiegokolwiek układu, który ma realizować funkcję logiczną opisaną algebrą Boole'a można sprowadzić do następującej formuły: istnieje pewna czarna skrzynka (black box), która posiada n wejść i m wyjść i powinna ona zrealizować pewne zadanie opisane za pomocą matematycznej formuły wg algebry Boole'a. Zadaniem inżyniera jest skonstruowanie „wnętrza” tej skrzynki. Załóżmy (a jest to bardzo istotne założenie), że stan wyjść naszej czarnej skrzynki zależy tylko i wyłącznie od tego, co jest na wejściu skrzynki. Jeżeli jest n wejść, to ilość możliwych kombinacji wartości sygnałów wejściowych wynosi 2ⁿ. Dla niektórych z kombinacji wejściowych na wyjściu (wyjściach) układu pojawi się logiczne 1 a dla innych logiczne 0. W jaki sposób można opisać działanie takiego układu. Najprościej za pomocą słów i opis ten można wyrazić tak aby zbudowany był w oparci u zdania logiczne połączone logicznymi spójnikami.

Przykład

Należy skonstruować układ cyfrowy, który będzie sterował pracą alarmu a opisany jest następująco:

alarm zostanie uruchomiony jeżeli jest włączony i drzwi nie są zamknięte lub jest po godzinie 18 i okno nie jest zamknięte

Zauważmy, że w opisie działania pojawiają się spójniki logiczne, które bezpośrednio pokażą nam, jaki taki układ skonstruować. Każde ze zdań oznaczymi literą według schamtu poniżej

alarm zostanie uruchomiony - Z

jest włączony - A

drzwi nie są zamknięte - B'

jest po godzinie 18 - C

okno nie jest zamknięte - D'

i wtedy całość możemy zapisać jako: Z = AB' + CD'. No i oczywiście zrealizować za pomocą układu.

Podejście to jednak nie zawsze może zostać użyte, bowiem w wielu przypadkach nie zawsze da się w taki sposób wyrazić opis działania projektowanego układu. Zauważmy, bowiem, że jeżeli w układzie mamy n wejść, to liczba możliwych kombinacji sygnałów wejściowych wynosi 2ⁿ i opis jego działania możemy podać także za pomocą tzw. tablicy prawdy, w której dla każdej kombinacji wejściowej podana zostanie wartość wyjścia (wyjść). Rozważmy prosty przykład.

Przykład

Mamy układ posiadający dwa wejścia A B (czyli cztery możliwe kombinacje sygnałów wejściowych) i wiemy, że opisuje go następująca tablica prawdy:

A	B	X
0	0	1
0	1	0
1	0	1
1	1	0

Z tablicy tej wynika, że na wyjściu X powinno pojawić się 1, gdy A = 0 i B = 0 lub A = 1 i B = 0. Bezpośrednie odczytanie tego zdania w sposób podobny do Przykładu prowadzi nas do możliwości zapisania zdania logicznego w postaci sumy dwóch iloczynów (zauważmy, że mamy (A = 0 i B = 0) - połączone zatem iloczynem - lub - połączone zatem sumą - (A = 1 i B = 0) - znów połączone iloczynem), ale musimy pamiętać, że o tym, że wartość tego zdania będzie prawdziwa wtedy, gdy choćby jedno ze zdań składowych występujących pomiędzy sumą logiczną będzie prawdziwe. Jednak, aby zdania te były prawdziwe (a są zbudowane jako iloczyny dwóch zmiennych), to każda z tych zmiennych musi mieć wartość 1. Aby tak się stało to te zmienne, które mają wartość 0 muszą zostać zanegowane, a te, które mają wartość 1 przepisane w postaci prostej. Zatem ostatecznie X = A'B'+AB', czyli układ zadziała kiedy nieprawdziwe będzie A i B lub prawdziwe będzie A i nieprawdziwe B. Postać taka nazywana jest sumą iloczynów (SOP) a składniki tej sumy nazywane są mintermami. Ale rozważania te można poprowadzić także od drugiej strony. Zauważmy, że można zapytać kiedy układ nie będzie działał. Otóż nie będzie działał kiedy (A = 0 lub B = 1) i (A = 1 lub B = 1). Wyrażenie to jest nieprawdziwe, jeżeli choćby jedno ze zdań składowych jest nieprawdziwe, ale jako, że zdania te budowane są za pomocą sumy logicznej (a ta zwraca wartość 1, gdy choć jedno ze zdań jest prawdziwe), to wszystkie zmienne, które mają wartość 0 muszą zostać wzięte w postaci prostej, a te które wartość 1 - w postaci zanegowanej. Postać taka nazywa się Iloczynem sum (POS)

Upraszczanie i minimalizacja funkcji logicznych - zastosowanie podstawowych praw algebry Boole'a, metoda siatek Karnaugha, metoda Quine'a-McCluskey'a.

Jak nietrudno zauważyć dla każdego urządzenia cyfrowego, które posiada n wejść ilość możliwych kombinacji sygnałów wejściowych wynosi 2ⁿ, co oznacza, że w ogólnym przypadku matematyczny opis funkcji realizowanej przez projektowane urządzenie może zawierać 2ⁿ mintermów bądź makstermów (w zależności od przyjętej postaci funkcji). Realizacja tego typu funkcji za pomocą funktorów, które następnie będą implementowane w postaci układów elektronicznych (sieci połączeń tranzystorów) może przysparzać wiele problemów nie tylko natury ekonomicznej (potrzeba użycia sporej liczby układów scalonych, czy też tranzystorów przejawiająca się kosztochłonnym procesem wytworzenia tego typu elementu, czy też - z racji tego, że użyte elementy konsumują energię elektryczną - dużą energochłonnością w czasie pracy takiego urządzenia i rozpraszaniem zużytej energii), ale i logistycznej - problemem staje się odpowiednie rozmieszczenie elementów w przestrzeni w układzie scalonym. M.in. z tych powodów wyrażenia logiczne upraszcza się dokonując tzw. minimalizacji funkcji logicznych. Istnieje kilka takich metod a w opracowaniu zaprezentowane będą jedynie trzy. W zasadzie wszystkie metody można sprowadzić do jednej „bazowej” czyli do zasad i reguł, jakie wynikają z praw algebry Boole'a. Prezentację poszczególnych metod zaczniemy od tzw. siatek Karnaugh'a a następnie przejdziemy do metody Quinne'a-McCluskey'a jednocześnie pokazując, jak działają w obu przypadkach prawa algebry Boole'a, czyli jak funkcjonuje metoda „bazowa”.

Nim zajmiemy się siatkami Karnaugh'a potrzebujemy pewnego wprowadzenia dotyczącego pewnego kodu, jaki jest używany w tej metodzie. Jest to tzw. kod Gray'a. Ideą tego kodu jest takie zakodowanie kolejnych słów bitowych aby sąsiadujące ze sobą słowa różniły się tylko wyłącznie na jednej pozycji. Istnieje kilka metod tworzenia tego kodu. Dla przykładu zaprezentowane będzie metoda tzw. lustra. Polega ona na tym, że kodowanie przy użyciu kolejnych bitów realizowane jest poprzez odbijanie w lustrze kolejnych ciągów bitów, przy czym nowe bity dopisujemy zawsze z lewej i po lewej stronie lustra są to zera, a po prawej są to jedynki.

Przykład 1x

Jednobitowy kod Gray'a ma postać:

• 1

Dwubitowy kod Graya tworzymy następująco:

Odbijamy w lustrze ustawionym tuż za jedynką (tu będzie to pionowa kreska) kod jednobitowy

0 1 | 1 0

a następnie dopisujemy zera i jedynki z lewej strony

00 01 11 10

Otrzymując w ten sposób kod dwubitowy. Kod trzybitowy można uzyskać analogicznie tym razem jednak lustro pojawi się za ciągiem 10 (tzn. zawsze pojawia się ono na końcu odbijanego kodu):

00 01 11 10 | 10 11 01 00

i znów dopisujemy zera i jedynki:

000 001 011 010 110 111 101 100

itd.

Zauważmy, że pomiędzy kolejnymi słowami kodu występuje różnica tylko na jednym bicie; są to tzw. słowa sąsiadujące. Ale nietrudno też zauważyć, że tego typu własność występuje pomiędzy skrajnymi słowami kodu a także wewnątrz samego kodu, bo oto pomiędzy słowem 000 a 010 też mamy różnicę tylko na jednym bicie - to także są sąsiadujące słowa w tym kodzie. Będziemy korzystali z tego kodu i jego własności przy budowie siatek Karnaugh'a.

Siatki Karnaugh'a zostały wprowadzone po to, aby usprawnić proces minimalizacji form boolowskich. Jest to metoda graficzna a jej podstawą są specjalne tablice, które dla kolejnych liczb zmiennych prezentowane są poniżej. Kolejne kolumny i wiersze oznaczane są za pomocą odpowiedniego n-bitowego kodu Gray'a zaś wiersze i kolumny odpowiadają użytym zmiennym. Kolejność zmiennych w kolumnach/wierszach może być dowolna, podobnie jak i ich liczba - niemniej jednak generalnie dba się o to, aby kształt siatek był kwadratem lub prostokątem, w którym w kolumnie lub wierszu będzie o jedną zmienną więcej (mniej) w porównaniu do wiersza/kolumny. W związku z tym, ze każda komórka w takiej tablicy ma określony adres w postaci ciągu zer i jedynek można im przypisać dziesiętne wartości wg przykładów poniżej.

A BC	0	1
00	0	4
01	1	5
11	3	7
10	2	6

Przykład 1xx

A B	0	1
0	0	1
1	2	3

AB C	00	01	11	10
0	0	2	6	4
1	1	3	7	5

AB CD		00		01	11		10
00		0		4	12		8
01		1		5	13		9
11		3		7	15		11
10		2		6	14		10
ABC DE	000		001		011			010		110		111	101	100
00	0		4		12			8		24		28	20	16
01	1		5		13			9		25		29	21	17
11	3		7		15			11		27		31	23	19
10	2		6		14			10		28		30	22	18

AB CDE		00		01	11		10
000		0		8	24		16
001		1		9	25		17
011		3		11	27		19
010		2		10	26		18
110		6		14	30		22
111		7		15	31		23
101		5		13	29		21
100		4		12	28		20
ABC DEF	000	001		011			010		110		111	101	100
000	0	8		24			16		48		56	40	32
001	1	9		25			17		49		57	41	33
011	3	11		27			19		51		59	43	35
010	2	10		26			18		50		58	42	34
110	6	14		30			22		54		62	46	38
111	7	15		31			23		55		63	47	39
101	5	13		29			21		53		61	45	37
100	4	12		28			20		52		60	44	36

W ten sposób można budować oczywiście siatki dla większej liczby zmiennych, ale jak się za moment okaże nie jest to powszechnie robione. Powodem będzie kwestia określenia tzw. sąsiedztwa komórek w tabeli.

W tak skonstruowane tabele wpisywane są jedynki lub zera (albo poziome kreski - dla tych funkcji, które dla pewnych kombinacji sygnałów wejściowych nie są określone) i następuje proces minimalizowania poprzez zakreślanie możliwie jak najmniejszej liczby jak największych grup minimalizacyjnych mających kształt kwadratu bądź prostokąta zbudowanych z liczby komórek, która wynosi: 1, 2, 4, 8, 16, 32, ... czyli 2ⁿ, n = 0, 1, 2, ... W przypadku siatek Karnaugh'a dla funkcji nie więcej niż 4 zmiennych problem zakreślania jest dość prosty. Należy jednak pamiętać, że skrajne wiersze i kolumny w tablicy ze sobą sąsiadują. Dlatego zakreślenia mogą przyjmować następującą formę:

W przypadku siatek dla liczby zmiennych większej niż 5 należy jednak pamiętać o ty, że realizowane zakreślenia muszą spełniać następującą zasadę: jeżeli przecinają istniejące w siatce osie symetrii, to zakreślenia muszą obejmować dokładnie taką samą liczbę komórek po obu stronach osi. Z tego też powodu niewłaściwym jest zakreślenie prezentowane poniżej.

Powinno ono być realizowane następująco:

Każde tego typu zakreślenie prowadzi do uproszczenia funkcji tzn. do jej zminimalizowania przy czym minimalizowania oznacza pozostawienie tylko tych zmiennych, od których rzeczywiście zależy wartość funkcji. Weźmy pod uwagę taki oto przykład.

Przykład

F(A,B,C)=Σ(0,1,3,4)=A'B'C'+A'B'C+A'BC+AB'C'

Jak łatwo można zauważyć pierwsze dwa min termy można uprościć następująco: A'B'C'+A'B'C = A'B'(C'+C) = A'B' co oznacza, że dla tych dwóch mintermów wartość funkcji nie zależy od zmiennej C, Ale ten tok rozumowania można także powtórzyć dla mintermów A'B'C+A'BC, bo A'B'C+A'BC = A'C(B'+B) = A'C wtedy dla powyższych dwóch mintermów wartość funkcji nie zależy od zmiennej B, ale także dla A'B'C'+AB'C', bo A'B'C'+AB'C' = B'C'(A'+A) = B'C' i dla tego przypadku wartość funkcji nie zależy od zmiennej A. Powyższe rozważania sugerują, że funkcję F można zapisać jako: A'B'+A'C+B'C', ale zauważmy, że można pójść o krok dalej i zapisać A'B'+A'C+B'C' = A'B'(C'+C)+A'C+B'C' = A'B'C'+A'B'C+A'C+B'C' = (A'+1)B'C + (B'+1)A'C = B'C+A'C i jest to możliwie najprostsza postać dla tej funkcji.

Zminimalizowanie tej funkcji za pomocą siatki Karnaugh'a jest bardzo proste i na tym przykładzie przedstawiona zostanie główna idea działania operacji minimalizowania przy użyciu siatek. W związku z tym, że minimalizowana funkcja jest przedstawiona za pomocą sumy mintermów w siatce Karnaugh'a dla czterech zmiennych w miejsca, w których dziesiętna wartość odpowiada mintermom funkcji F wpisujemy jedynki (`1'), natomiast w pozostałe miejsca zera (`0'). Funkcję będziemy minimalizować „w jedynkach” (równie dobrze moglibyśmy minimalizować ją „w zerach” i otrzymamy dokładnie ten sam wynik - to zostanie jeszcze pokazane) starając się zakreślić możliwie jak najmniej jak największych grup minimalizacyjnych. Jak widać, takich grup możemy zakreślić 3, ale wystarczą już dwie, by pokryć wszystkie grupy jedynkowe. Pierwsza grupa obejmuje mintermy A'B'C' i AB'C'. Gdyby zastosować prawa algebry Boole'a to mintermy te można uprościć do postaci B'C', co niniejszym oznacza, że pozbywamy się zmiennej A. W związku z tym w przypadku minimalizacji w siatkach Karnaugh'a każde zakreślenie grupy powoduje eliminację tej zmiennej, której wartość zmienia się w obrębie grupy z 0 na 1 i vice versa. W obrębie pierwszej grupy zmieniła się wartość zmiennej A zatem ona jest eliminowana. Pozostałe zmienne pozostają i jeżeli minimalizujemy „w jedynkach” to te zmienne, które mają wartość 0 brane są do mintermu jako zanegowane, a te które mają wartość 1 w postaci prostej. Podobnie postępujemy w przypadku drugiej grupy. Tym razem jednak zmienia się wartość zmiennej B, co oznacza, że minterm można zminimalizować do postaci A'C (z praw algebry Boole'a byłoby to A'B'C+A'BC = A'C(B'+B) = A'C). Ostatecznie więc funkcja ma postać F(A,B,C)=Σ(0,1,3,4)= B'C+A'C

Oczywiście prostota przykładu nie pokazuje, co by było gdyby grupa obejmowała dwie kolumny i dwa wiersze lub co by było gdyby pojawiły się zakreślenia, takie jak dla siatek Karnaugh'a 5-u czy też 6-u zmiennych. Oczywiście metoda działa nadal tak samo, ale poniżej kilka przykładów na bazie wcześniejszych ilustracji przy założeniu, że minimalizujemy „w jedynkach”.

Przykłady narysowane

Jak zostało już wspomniane minimalizować można „w zerach”. Robi się to, gdy funkcja jest podana za pomocą iloczynu makstermów, ale można także zrobić, gdy funkcja podana jest w postaci sumy zakreślając zera. Ostateczny wynik będzie zawsze ten sam, co wynika z zasady dualności. Należy jednak pamiętać, że jeżeli zakreślamy „w zerach” to zmienne, które są zerami pozostawiamy w postaci prostej, a negujemy zmienne, które mają wartość jeden. Nadto skoro mamy funkcję w postaci iloczynu sum, to również i w czasie jej minimalizacji musimy ją tak zapisać. Dla przykładu omawianego wyżej będzie to: (A'+C')(B'+C). Jak widać jest to nieco inna postać funkcji niż podana wyżej, ale: (A'+C')(B'+C) = A'B'+A'C+C'B'+C'C = A'B'+A'C+B'C' = A'B'(C'+C)+A'C+B'C' = A'B'C'+A'B'C+A'C+B'C' = (A'+1)B'C + (B'+1)A'C = B'C+A'C, czyli dokładnie tak samo, jak przy minimalizacji w jedynkach.

Wróćmy w tym miejscu na moment do nietypowych zakreśleń, jakie były robione w przypadku siatek dla 5-u i 6-u zmiennych. Dlaczego są one w ogóle możliwe. Otóż jest to przede wszystkim wynik działania praw algebry Boole'a.

Przykład

Dla zakreślenia jak na rysunku poniżej można zapisać dwa zminimalizowane mintermy: , ale nie trudno zauważyć, że można dalej posłużyć się algebrą Boole'a i wyrażenie to doprowadzić do postaci: co oznacza, że dwie zakreślone ze sobą grupy sąsiadują mimo, iż nie jest to widoczne w siatce Karnaugh'a. Zauważmy jednak, iż arbitralnie przyjęliśmy kolejność wpisywania zmiennych w lewym górnym rogu siatki. Gdyby ta kolejność była nieco inna, np. taka, to okazuje się, że zakreślenie miałoby zdecydowanie inny kształt i wyżej opisana sytuacja, by nie wystąpiła.

///rysunki

Jak do tej pory zajęliśmy się dwiema często spotykanymi metodami minimalizacji funkcji logicznych. Teraz pora na metodę trzecią, czyli metodę Quine'a-McCluskey'a.

Przykład

Ideę działania metody Quine'a-McCluskey'a pokażemy na przykładzie minimalizacji funkcji G(A,B,C,D) = Σ(0,3,4,5,7,11,13,15). W metodzie tej w pierwszej kolejności należy wypisać wszystkie brane pod uwagę mintermy (makstermy) i pogrupować je względem liczby występujących w nich bitów 1 (od najmniejszej liczby do największej). Każdą taką grupę można podkreślić:

(0)	0000
(4)	0100
(3)	0011
(5)	0101
(7)	0111
(11)	1011
(13)	1101
(15)	1111

Następnie pomiędzy wszystkimi mintermami (makstermami) z grupy pierwszej i drugiej, drugiej i trzeciej, trzeciej i czwartej, itd. (czyli pomiędzy grupami sąsiadującymi) sprawdzamy, czy istnieją takie min termy (makstermy), które różnią się tylko i wyłącznie na jednej pozycji (na jednym bicie). Jeżeli tak, to łączymy razem takie dwa mintermy (makstermy) tworząc z nich jeden nowy, a bit, na których się różnimy zastępujemy znakiem `-`.Te mintermy (makstermy), które zostały użyte w czasie minimalizowania oznaczamy literką `v', te zaś, które nie - znakiem `*'. Wyżej opisaną operację powtarzamy do póki istnieje taka możliwość za każdym razem segregując minimalizowane mintermy (makstermy) względem liczby jedynek. Jeżeli w kroku ostatnim zminimalizowane mintermy powtarzają się tzn. różni się w nich jedynie kolejność mintermów (makstermów), to wykreślamy je.

(0)	0000	v	(0,4)	0-00	*	(3,7,11,15)	--11	*
(4)	0100	v	(4,5)	010-	*	(3,11,7,15)	--11
(3)	0011	v	(3,7)	0-11	v	(5,7,13,15)	-1-1	*
(5)	0101	v	(3,11)	-011	v	(5,13,7,15)	-1-1
(7)	0111	v	(5,7)	01-1	v
(11)	1011	v	(5,13)	-101	v
(13)	1101	v	(7,15)	-111	v
(15)	1111	v	(11,15)	1-11	v
			(13,15)	11-1	v

Mintermy (makstermy) oznaczone `*' są tymi, które dalej nie dają się zminimalizować zatem należy wziąć je celem zapisania zminimalizowanej postaci funkcji, ale można zauważyć, że nie SA one wszystkie potrzebne. Dla przykładu ze zminimalizowanych mintermów (0,4) i (4,5) potrzebny jest tylko jeden (0,4), bo (4,5) oznacza pokrycie, które nie jest konieczne (tzn. byłoby konieczne, gdyby uwzględniać problem hazardu). Kwestia ta jest rozwiązywana w następnym etapie minimalizacji, w którym wypełniania jest specjalna tablica pokryć. W tablicy tej pionie zapisywane są wszystkie zminimalizowane mintermy (makstermy) oznaczone symbolem `*', a w górnym wierszu wszystkie mintermy (makstermy) funkcji. Głównym zadaniem tej tablicy jest wskazanie, które zminimalizowane mintermy (makstermy) są niezbędne aby pokryć wszystkie implikanty proste funkcji. Wypełnianie tej tablicy rządzi się następującymi regułami. W pierwszej kolejności należy wziąć pod uwagę te zminimalizowane implikanty, w których implikanty proste pokrywane są tylko raz (w przykładzie jest to (0,4), w następnej kolejności, te które pokrywają możliwie jak najwięcej implikantów. W reszcie przypadków dobór jest dowolny. Jeżeli zminimalizowany minterm (maksterm) pokrywa jakiś implikant prosty, to w tablicy oznacza się to symbolem `*' a obok takiego zminimalizowanego mintermu (makstermu) stawia znak `v'.

		0	3	4	5	7	11	13	15
V	(0,4)	*		*
	(4,5)
V	(3,7,11,15)		*			*	*		*
V	(5,7,13,15)				*	*		*	*

Z analizowanego przykładu widać, że zminimalizowany implikant (4,5) nie musi być brany pod uwagę. Ostatecznie postać funkcji określana jest na bazie tych zminimalizowanych mintermów, które zapewniają pokrycie dla wszystkich implikantów prostych. Robi się to w następujący sposób. W pierwszej kolejności wybierane są te zminimalizowane implikanty, które tylko jeden raz pokrywają implikanty proste (on po prostu muszą zostać wybrane, bowiem bez nich minimalizowana funkcja nie działałaby prawidłowo), Następnie pod uwagę brane są te zminimalizowane implikanty, które pokrywają możliwie jak największą liczbę implikantów prostych - one bowiem gwarantują, że funkcja faktycznie będzie zminimalizowana. W doborze pozostałych zminimalizowanych implikantów należy kierować się zasadą, aby za ich pomocą pokryć możliwie jak największą liczbę pozostałych implikantów prostych.

Projektowanie prostych układów kombinacyjnych

Nadchodzi czas by zająć się praktycznym wykorzystaniem prezentowanych do tej pory kwestii i rozpocząć projektowanie prostych układów kombinacyjnych. Ich realizację pokażemy na przykładzie prostych zadań, jakie należy rozwiązać podając sprzętowo realizację. W przypadku układów kombinacyjnych zasada postępowania jest niemal zawsze taka sama: tablica prawdy, minimalizacja, realizacja układu. Najczęściej jako metodę minimalizacyjną wybiera się siatki Karnaugha.

Przykład

Zaprojektować układ, który stwierdzi, że czterobitowa liczba binarna X podana na jego wejście jest z zakresu X∈ <0,5) v <8,12) tzn. układ zwróci na wyjściu 1 jeżeli podana na jego wejście liczba będzie z w/w zakresu. Układa posiada więc cztery wejścia i jedno wyjście.

Jak widać podawane na wejście będą liczby czterobitowe i oznaczmy ich bity (od najstarszego do najmłodszego) A,B,C,D. W pierwszym kroku tworzymy tablicę prawdy:

A	B	C	D	X
0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

Załóżmy, że będziemy realizowali funkcję w postaci SOP, zatem do siatki Karnaugha, w odpowiednie miejsca wpisujemy jedynki i dokonujemy minimalizacji zgodnie z znanymi już regułami.

Jako wynik otrzymujemy X=B'+A'C'D'

Przykład

Zaprojektować układ, który zbada, czy liczba jedynek w słowie 4-bitowym jest parzysta; jeżeli tak, to powinien wygenerować na wyjściu 1.

Tym razem mamy do czynienia z układem, który posiadał będzie 4 wejścia i jedno wyjście. Zapisujemy tablicę prawdy i w każdym jej wierszu po prostu liczymy liczbę jedynek. Jeżeli jest parzysta, to w kolumnie Y piszemy 1. W związku z tym, że 0 też jest liczbą parzystą (!), to w tym wierszu także piszemy 1.

A	B	C	D	Y
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	1
0	1	1	1	0
1	0	0	0	0
1	0	0	1	1
1	0	1	0	1
1	0	1	1	0
1	1	0	0	1
1	1	0	1	0
1	1	1	0	0
1	1	1	1	1

Tworzymy siatkę Karnaugh'a i jej pobieżna analiza pokazuje nam, że zbyt wielkiej swobody w minimalizowaniu nie mamy, bowiem w siatce znajduje się osiem grup minimalizacyjnych a w każdej po jednej jedynce. Ale, jak się wkrótce okaże, to nie będzie dla nas problemem.

Y = A'B'C'D' + A'B'CD + A'BC'D + A'BCD' + ABC'D' + ABCD + A'BC'D + A'BC'D

Powyższe wyrażenie możemy uprościć stosując znane nam prawa algebry Boole'a

Y = A'B'(C'D' + CD) + A'B(C'D + CD') + AB(C'D' + CD) + AB'(C'D + C'D) =

A'B'(C⊗D) + A'B(C⊕D) + AB(C⊗D) + AB'(C⊕D) =

(C⊗D)(A'B' + AB) + (C⊕D)(A'B + AB') =

(C⊗D)(A⊗B) + (C⊕D)(A⊕B).

Zauważmy, że (x⊗y) = (x⊕y)', co oznacza, że powyższe wyrażenie możemy zapisać jako

(C⊗D)(A⊗B) + (C⊗D)'(A⊗B)' = A⊗B⊗C⊗D

i jak widać pozornie „beznadziejny” przypadek okazuje się być bardzo prosty.

//schemat

Przykład

Zaprojektować układ, który będzie komparatorem tzn. stwierdzi, którą z relacji: `>', `=' lub `<' spełniają dwie 4-bitowe liczby podane na jego wejście. Układ ten należy zaprojektować w wersji szeregowej tzn. liczby będą sprawdzane bit po bicie oraz w wersji równoległej, tzn. sprawdzone będą wszystkie bity na raz.

Komparator jest układem, który posiada 3 wyjścia: `>', `=' oraz `<' i w zależności od przyjętego rozwiązania może posiadać labo 5 wejść (komparator szeregowy), albo 2n wejść, gdzie n oznacza liczbę porównywanych bitów w liczbie (komparator równoległy). W pierwszej kolejności rozwiążemy to zadanie dla projektu komparatora szeregowego, tzn. zbudujemy moduł, który będzie dokonywał porównania na jednym bicie bazując na informacji dotyczącej bitów z przetwarzanej pozycji oraz na informacji przekazywanej z pozycji wcześniejszej. Porównanie będzie realizowane od lewej do prawej tzn. od bitu najstarszego do najmłodszego, co wynika z obserwacji, że najstarsze bity mają decydujący wpływ na określenie, czy dwie liczby są `>', `=' czy też `<'. Zatem nasz układ będzie posiadał 5 wejść i 3 wyjścia.

Najpierw zajmiemy się określeniem kiedy dwa bity, X i Y, są `>', `=' albo `<':

- X > Y tylko wtedy, gdy X = 1 i Y = 0 tzn. X>Y można opisać za pomocą funkcji XY';

- X = Y albo gdy X = 0 i Y = 0, albo gdy X = 1 i Y = 1 tzn. X=Y można zapisać za pomocą funkcji X⊗Y;

- X < Y tylko wtedy, gdy X = 0 i Y = 1 tzn. X<Y można opisać za pomocą funkcji X'Y.

Teraz zastanówmy się w jaki sposób „ręcznie” porównywalibyśmy dwie liczby pozycja po pozycji bazując na informacjach z pozycji aktualnej oraz z pozycji wcześniejszej. Aktualną pozycję oznaczmy indeksem n a pozycję wcześniejszą indeksem n+1. Zauważmy, że jeżeli na pozycji wcześniejszej zachodzi np. A_n+1>B_n+1, to nie ma zupełnie znaczenia, to co dzieje się na pozycji aktualnej (na następnych z resztą też), czyli A>B (liczba A jest większa od liczby B). Jeżeli jednak na pozycji wcześniejszej było A_n+1=B_n+1, to aby po pozycji o indeksie n zachodziło A>B (liczba A była większa od liczby B) na pozycji aktualnej (tzn. o indeksie n) musi zachodzić A_n>B_n. Ostatecznie A>B (liczba A jest większa od liczby B), gdy A_n+1>B_n+1 lub A_n+1=B_n+1 i A_n>B_n. Ten sam tok rozumowania można powtórzyć w przypadku gdy A_n+1>B_n+1, tzn. A<B (liczba A jest mniejsza od liczby B), gdy A_n+1<B_n+1 lub A_n+1=B_n+1 i A_n<B_n. W przypadku gdy A_n+1=B_n+1 oraz A_n=B_n, to liczby A i B mogą być równe, ale o tym można przekonać się dopiero analizując wszystkie ich bity.

Nasze rozważania można przeprowadzić także bazując na siatkach Karnaugh'a, które dla wyjścia A>B moją postać:

dając po minimalizacji funkcję: A_n+1>B_n+1 + A_n+1=B_n+1∙A_n∙B_n'

Dla wyjścia A=B są natomiast w postaci:

dając po minimalizacji funkcję: A_n+1=B_n+1∙A_n=B_n

Realizacja za pomocą bramek pojedynczego modułu dokonującego komparacji na pojedynczym bicie wygląda następująco:

// rys

W przypadku realizacji komparatora równoległego tworzymy układ, który ma za zadanie dokonać operacji porównania wszystkich bitów jednocześnie. W komparatorze szeregowym wynik na pozycji n zależy nie tylko od wyniku na pozycji n+1, ale także na pozycji n+2 itd. Innymi słowy ostateczne rozstrzygnięcie, czy np. liczba A>B wymaga sprawdzenia bit po bicie wszystkich n pozycji i propagacja tej informacji może dość wolno zachodzić (podobnie jak się to dzieje w sumatorze - kwestia ta będzie jeszcze wyjaśniona). Jednak bazując na dotychczasowym podejściu oraz przyjmując arbitralnie np. liczbę bitów n=4 zauważmy, że A>B, gdy A3>B3, ale gdy się zdarzy, że A3=B3, to należy wziąć pod uwagę czy A2>B2 pamiętając, że A3=B3, jeżeli jednak i A2=B2, to trzeba sprawdzić dalej itd. co można wyrazić w postaci zapisu: A>B gdy A₃>B₃ lub A₃=B₃ i A₂>B₂ lub A₃=B₃ i A₂=B₂ i A₁>B₁ lub A₃=B₃ i A₂=B₂ i A₁=B₁ i A₀>B₀. Stąd funkcja F_A>B = A₃∙B₃' + A₃⊗B₃∙A₂B₂' + A₃⊗B₃∙A₂⊗B₂∙A₁B₁' + A₃⊗B₃∙A₂⊗B₂∙A₁⊗B₁∙A₀B₀'. Ten sam tok rozumowania można powtórzyć dla A<B.

W przypadku A=B muszą być równe wszystkie bity, czyli A₃=B₃ i A₂=B₂ i A₁=B₁ itd. zatem F_A=B=A₃⊗B₃∙A₂⊗B₂∙A₁⊗B₁∙A₀⊗B₀.

Jak widać różnica pomiędzy obydwoma komparatorami jest dość subtelna (w zasadzie one są skonstruowane w oparciu o zbliżone podejście): w pierwszym przypadku mamy jednobitowe moduły, które możemy łączyć szeregowo, zaś w drugim jeden kompletny układ.

Sumator jedno i wielobitowy

Jak do tej pory projektowaliśmy kilka prostych układów kombinacyjnych, które miały różnorakie zastosowanie. Generalnie były to różnego typu konwertery kodów jakie stosuje się powszechnie w informatyce ale także zaprojektowaliśmy układ generacji bitu kontroli parzystości kiedy to okazało się, ze metoda siatek Karnaugh'a w czasie minimalizacji nas zawiodła, bo postać minimalną funkcji uzyskaliśmy dzięki zastosowaniu algebry Boole'a o dość skomplikowanym zabiegom. Tym razem chcemy jednak zaprojektować bardziej „praktyczny” układ - będzie to sumator jednobitowy, którego zadanie będzie dodawanie dwóch bitów liczby. Nim to uczynimy należy przyglądnąć się operacji dodawania jaką robimy w formie pisemnej dla dziesiętnego systemu liczbowego. Zauważmy, że poznaliśmy już w jaki sposób wykonuje się dodawanie w systemie binarnym, ale tak naprawdę nie operacja ta nie została głębiej przeanalizowana, choć na pierwszy rzut oka wydaje się ona być niezwykle banalna.

Przykład

Należy dodać pisemnie do siebie dwie liczby w systemie dziesiętnym: 125 + 439.

0	0	1		przeniesienie
	1	2	5	składnik
+	4	3	9	składnik
=	5	6	4	suma

Operację dodawania dokonujemy pozycja po pozycji. Taka więc mamy: 5 + 9 = 4 (przeniesienie 1), dalej 1 + 2 + 3 = 6 (przeniesienie 0) oraz 1 + 4 = 5 (przeniesienie 0). Można więc zauważyć, że w ostateczności na każdej pozycji dodajemy do siebie dwie cyfry składnika oraz ewentualne przeniesienie z pozycji wcześniejszej, a jako wynik otrzymujemy sumę i ewentualne przeniesienie. W zasadzie sprawę można potraktować bardziej ogólnie: sumowanie dwóch liczb polega na dodawaniu pozycja po pozycji trzech cyfr i jako wynik otrzymuje się sumę i przeniesienie. Taka sama zasada obowiązuje w przypadku systemu binarnego, ale trzeba pamiętać, że tam do dyspozycji jest tylko 0 i 1 oraz, że 1+1=0. Zaprojektujemy więc układ sumatora jednobitowego. Będzie posiadał trzy wejścia x_i, y_i, c_i-1 i dwa wyjścia: s_i i c_i. x_i i y_i to ite bity dodawanej liczby, c_i-1 oznacza przeniesienie z pozycji poprzedniej, s_i sumę na itej pozycji a c_i przeniesienie z itej pozycji.

Przykład

Projekt sumatora jednobitowy. Tablica prawdy

xi	yi	ci-1	si	ci
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Dokonujemy minimalizacji w siatkach Karnaugha zarówno dla wyjścia s_i jak i c_i.

W przypadku sumy si mamy na pierwszy rzut oka dość beznadziejną sytuację bowiem musimy zakreślić 4 grupy, które dają nam (wyjątkowo posłużymy się klasyczną notacją):

czyli suma arytmetyczna jest obliczana jako operacja EX-OR trzech wejść.

W przypadku przeniesienia c_i mamy:

,

ale postać tę bardzo często modyfikuje się pisząc

.

Pomimo iż w tym przypadku w nawiasie zamiast sumy (+) mamy EX-OR (⊕), to wartość całego wyrażenia nie zmienia się, a w rezultacie upraszcza nam konstrukcję całego układu, bo dla sumy s_i już raz liczymy x_i ⊕ y_i zatem możemy wartość tego wyrażenia wykorzystać do obliczenia c_i.

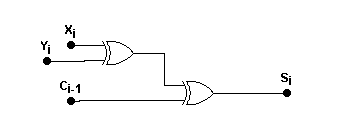
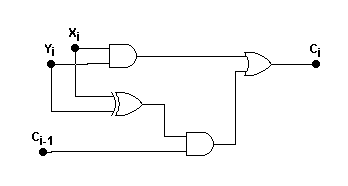
W rezultacie cały nasz skonstruowany układ możemy zamknąć w czarnej skrzynce, które schematycznie wygląda tak:

Oczywiście skrzynka wykonuje operacje dodawania tylko na jednym bicie, ale dość łatwo można dojść do wniosku, że większa liczba dodawanych bitów wymaga zastosowania większej liczby takich sumatorów połączonych szeregowo tzn. jeden za drugim wg poniższego schematu.

Konstrukcja jest bardzo prosta i może w zasadzie być zastosowana nawet do dodawania 64 bitowych liczb. Posiada jednak pewną zasadniczą wadę. Zauważmy bowiem, że w zasadzie nasz sumator jest realizowany w oparciu o układy elektroniczne, których jedną z immanentnych cech jest wprowadzanie tzw. opóźnienia. Nasze funktory logiczne działają w oparciu o przepływający przez kolejne elementy bramek prąd elektryczny, który jednak ulega w każdym z nich małemu opóźnieniu Δτ. Zatem aby w takim sumatorze uzyskać wynik sumy na 31 pozycji (czyli 32 bicie) potrzebna jest wartość przeniesienia z pozycji 30, ale ta może pojawić się gdy znana jest wartość przeniesienia z pozycji 29 itd. Zatem każdy pośredni sumator musi czekać (z racji tego, że na każdym jego stopniu pośrednim występują niewielkie opóźnienia) na swoich poprzedników, a ten ostatni musi poczekać aż na 31 poprzedników. Jeżeli każdy ze stopni wprowadza takie samo niewielkie opóźnienie Δτ, to w efekcie na ostatnim stopniu będzie trzeba poczekać 31∙ Δτ. Czyli w wyżej prezentowanym sumatorze dodawanie jest realizowane dosyć wolno (!!!), bo proporcjonalnie do liczby stopni, ale istnieje możliwość częściowego ominięcia tego kłopotu. Służy temu sumator CLA.

Sumator typu carry look ahead (CLA)

Idea budowy sumatora CLA wywodzi się z chęci uniknięcia niedogodności jakie niesie w sobie sumator klasyczny, szeregowy. Zauważmy bowiem, że podstawowym problemem jest tu kwestia tzw. propagacji przeniesień na poszczególne stopnie sumatora. Aby rozwiązać ten problem należy wrócić do równania opisującego przeniesienie na itej pozycji. Mamy tam bowiem:

Podstawmy więc za kolejne i liczby 0, 1, 2, ...

Dla i = 0 będzie:

Przy czym c_-1 oznacza tu przeniesienie, które zwykle równe jest 0 zatem wartość logiczną tego wyrażenia można policzyć jako:

Dla i = 1 będzie:

Ale skoro znamy z poprzedniego równania c₀, to możemy zapisać:

Dla i = 2 będzie:

Ale skoro i tu znamy z poprzedniego równania c₁, to możemy zapisać:

Tak samo możemy postąpić dla i = 3, wtedy

itd.

Zauważmy, że w ten sposób dostajemy kolejne formuły logiczne pozwalające wyrazić nam przeniesienie na kolejnych pozycjach nie za pomocą przeniesień z pozycji wcześniejszych, ale za pomocą wartości bitów z wcześniejszych pozycji. Oczywiście można sobie wyobrazić, ze formuła logiczna opisująca przeniesienie na 31 pozycji będzie długa na 2-ie strony (strzelam tu, bo nie sprawdzałem tego), ale pozwoli ona na jednoczesne wygenerowanie wartości przeniesień na każdej pozycji. Oczywiście słowo jednoczesne powinno być tu rozumiane dość ostrożnie, bowiem jak widać dla i = 3 formuła dość szybko staje się coraz dłuższa, a to wymaga zastosowania sporej ilości bramek logicznych, które nadal będą wprowadzały opóźnienia, zatem na pozycji i=31 nadal trzeba będzie czekać na wygenerowanie przeniesienia, ale już nie tak długo jak w przypadku sumatora zwykłego. Pozostaje tu także kwestia sporego skomplikowania samego układu sumatora cyfrowego, ale to już nie nasze zmartwienie, tylko projektantów i elektroników.

Rys.

Układ TC01 (True Compliment 0 1)

Zajmijmy się teraz zaprojektowaniem dość specyficznego układu. Jego zadanie będzie zrealizowanie następującej tablicy prawdy:

E	W	wy
0	0	0
0	1	1
1	0	we
1	1	we'

Układ posiada trzy wejścia: E, W i we oraz jedno wyjście wy. Sitaka Karnaugha wygląda następująco

i uzyskujemy z niej:

Realizacja układu za pomocą bramek.

Zauważmy, że układ ten obsługuje tylko i wyłącznie jeden bit wejścia. Gdybyśmy chcieli, aby obsługiwanych było więcej wejść, to musimy powielić go tyle razy ile jest to wymagane, a wszystkie wejścia E i W połączyć razem. Należy także pamiętać, że wtedy kombinacja E =0 W = 1 generuje na każdym z wyjść bit 1, zatem w czterobitowym układzie zostanie wygenerowanych cztery jedynki, a w szesnastobitowym aż szesnaście.

Do czego może posłużyć takie proste urządzenie zobaczymy dalej; choć trudno w to uwierzyć, to jest ono stosowany niemal w każdej jednostce arytmetyczno logicznej

Układ jednostki arytmetyczno logicznej (ALU). Szyna sterowania, kody sterowania, asembler

Wydawać by się mogło, że wszystko to, co do tej pory zostało przedstawione, jest w pewnym sensie zabawą bazującą na „kombinowaniu przy zerach i jedynkach”. Niemniej jednak przy odrobinie wysiłku jesteśmy w stanie pokazać, że wykorzystując niemal wszystkie do tej pory poznane elementy, można zbudować urządzenie, które wykona dla nas kilka pożytecznych prac. Aby tego dokonać musimy w odpowiedni sposób wykorzystać naszą dotychczasową wiedzę i połączyć nasze dotychczas opracowane układy w jeden. Będzie to Jednostka Arytmetyczno-Logiczna (ang. Arithemtic Logic Unit ALU), czyli ten moduł systemu komputerowego, w którym wykonywane są podstawowe operacje arytmetyczne i logiczne. Schemat jednostki prezentowany jest na rysunku poniżej. Co prawda w opracowaniu nie zostały przedstawione czym jest taki element jak rejestr (a w układzie jest ich aż dwa), ale możemy wyobrazić sobie, ze jest to swoistego rodzaju czarna skrzynka, w której można przechowywać przez pewien czas bity informacji. W naszym układzie takich rejestrów jest dwa i oznaczone są odpowiednio Rejestr X i Rejestr Y. Będą w nich przechowywane dwie liczby, które będziemy zamierzali przetwarzać w układzie.

Liczby te będą jedynie 4-bitowe, ale nic nie stoi na przeszkodzie by miały nawet 64 bity. Wyjścia obu rejestrów są podpięte do 4-bitowych układów TC01, które można sterować za pomocą sygnałów E_X, W_X, E_Y, W_Y. Z kolei wyjścia tych układów podpięte są do wejść sumatora 4-bitowego (jak widać zmienił się trochę jego symbol, ale nie ma to większego znaczenia; ten prezentowany na rysunku bardziej oddaje istotę pracy naszego układu), który może być zrealizowany w postaci sumatora szeregowego lub CLA - w tym przypadku jest to sprawa bez znaczenia. Sumator posiada także wejście c_-1, na którym normalnie jest podany sygnał (logiczne) 0, więc nie wpływa to na wynik dodawania, ale w tym przypadku będzie on wykorzystywany jako piąty sygnał sterujący całego układu. Innymi słowy sumator będzie dodawał do siebie wartości, jakie pojawią się na wyjściach obu układów TC01 plus to, co zostanie podane na wejście c_-1, czyli albo 0 albo 1. Na wyjściu sumatora, S_i, pojawi się wynik pracy sumatora. W układzie rzeczywistym wyjście to jest z powrotem podpięte do Rejestru X, który nazywany jest tzw. akumulatorem (zostało to oznaczone linią przerywaną), czyli układem przechowywania wartości ostatniego wyniku pracy sumatora. Na wyjściu c₃ pojawi się ewentualna informacja o przeniesieniu (przekroczeniu zakresu), ale w zasadzie nas najbardziej interesowało będzie to, co pojawi się na wyjściu S_i.

Praca układu będzie zatem sterowana pięcioma sygnałami, które będą wpływały na to, co ostatecznie wygeneruje na swoim wyjściu S_i sumator. Jako, że wejść sterujących jest 5 mamy do dyspozycji 2⁵=32 kombinacji sygnałów sterowania. Naszym zadaniem będzie sprawdzenie, jakie operacje zostały wykonane dla poszczególnych sygnałów sterujących. Można domniemywać, że pewne kombinacje tych sygnałów będą robiły „rzeczy” bezsensowne, ale jak się wkrótce okaże nie będzie ich aż tak wiele. Prześledzimy pracę tego układu dla najbardziej charakterystycznych kombinacji oraz dodatkowo podamy nazwy operacji jakie zrealizuje nasze ALU. Nazwy te są najczęściej określane jako tzw. mnemoniki, czyli operacji tzw. asemblera. Jest to język tzw. niskiego poziomu, który służy do programowania różnego typu mikroprocesorów i swego czasu był bardzo często wykorzystywany przez programistów. Wątek ten jednak rozwiniemy na końcu.

Zacznijmy więc naszą analizę. Kolejne kombinacje sygnałów sterujących zaprezentujemy w tabeli i będziemy zastanawiali się, co one potrafią zrobić.

EX	WX	EY	WY	c-1
1	0	1	0	0

Zauważmy, że w tym przypadku oba sygnały E_X i E_Y = 1 oraz W_X i W_Y = 0, co oznacza, że liczby zapisane w Rejestrze X i Rejestrze Y zostaną przepisane na wejście sumatora. Nadto c_-1 = 0, zatem sumator wykona operacje X + Y + 0, czyli wykona zwykłe dodawanie (zatem zrealizuje to, do czego został „stworzony”). Nie jest to zbyt „ciekawy” przypadek, ale czynność przezeń wykonaną można nazwać za pomocą mnemonika jako ADD(X,Y) (lub SUM(X,Y)).

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	0	1	0	0		X+Y+0		ADD(X,Y)

Zmieńmy teraz kombinację sygnałów sterujących na poniższą:

EX	WX	EY	WY	c-1
1	0	0	0	1

Tym razem tylko E_X = 1, zaś E_Y = 0 oraz W_X i W_Y = 0, co oznacza, że tylko liczba zapisana w Rejestrze X zostanie podana na wejście sumatora, bowiem wartość zapisana w Rejestrze Y zostanie w czasie przejścia przez TC01 „wyzerowana”. Tym razem c_-1 = 1, zatem sumator wykona operacje X + 0 + 1, czyli zwiększy wartość liczby X o 1. Innymi słowy dokona inkrementacji X, co można nazwać za pomocą mnemonika jako INC(X). Oczywiście nie trudno zauważyć, że gdyby E_X = 0, zaś E_Y = 1, to zostałaby zwiększona o 1 wartość liczby Y.

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	0	0	0	1		X+0+1		INC(X)
0	0	1	0	1		0+Y+1		INC(Y)

Jak widać nasze ALU potrafi już dodawać zawartości obu rejestrów oraz inkrementować wartość każdego z rejestrów osobno (oczywiście cały czas nasze urządzenie nie robi nic innego jak tylko de facto dodaje). Czy może zrobić coś jeszcze? Rozważmy następującą kombinację sygnałów sterujących na poniższą:

EX	WX	EY	WY	c-1
1	1	0	0	0

Tym razem tylko E_X = 1 i W_X = 1, zaś E_Y i W_Y = 0, co ponownie oznacza, że tylko liczba zapisana w Rejestrze X zostanie podana na wejście sumatora (wartość zapisana w Rejestrze Y jest nadal w czasie przejścia przez TC01 „zerowana”), ale W_X = 1 oznacza negację tego każdego bitu przechodzącego przez TC01 zatem na wejście sumatora zostanie podana zanegowana liczba X. Jako, że c_-1 = 0, to sumator wykona operację X' + 0 + 0, czyli na wyjściu S_i pojawi się zanegowana zawartość Rejestru X. Taką operacje można oznaczyć jako CMPL(X). Oczywiście ten sam tok rozumowania można powtórzyć dla liczby zapisanej w Rejestrze Y (tym razem jednak wymagane będzie, aby E_Y = 1 i W_Y = 1, zaś E_X i W_X = 0) i na wyjściu S_i pojawi się negacja Rejestru Y (czyli CMPL(Y)).

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	1	0	0	0		X'+0+0		CMPL(X)
0	0	1	1	0		0+Y'+0		CMPL(Y)

Można się zastanowić, co by było, gdyby w rozważaniach powyżej założyć, że c_-1 = 1, czyli:

EX	WX	EY	WY	c-1
1	1	0	0	1

Oczywiście sumator wykona wtedy operację X' + 0 + 1, czyli dokona inkrementacji zanegowanej wartości Rejestru X. Z pozoru wydaje się, że jest to operacja pozbawiona sensu, ale gdyby wrócić do początku naszego opracowania, to można zauważyć, że takie postępowanie jest już nam znane, bowiem wykonanie operacji: `zaneguj bity i dodaj jeden' jest charakterystyczne dla uzyskiwania reprezentacji liczb ujemnych w kodzie U₂. Niniejszym oznacza to, że nasze ALU jest w stanie wygenerować na swoim wyjściu liczbę ze znakiem przeciwnym zarówno w przypadku zawartości Rejestru X (dla E_X = 1 i W_X = 1, zaś E_Y i W_Y = 0 oraz c_-1 = 1) jak i Rejestru Y (E_Y = 1 i W_Y = 1, zaś E_X i W_X = 0 oraz c_-1 = 1). Taką operacje można oznaczyć mnemonikiem jako NEG(∙).

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	1	0	0	1		X'+0+1		NEG(X)
0	0	1	1	1		0+Y'+1		NEG(Y)

Skoro więc nasze ALU potrafi generować liczby ujemne (ze znakiem minus), to rodzi się naturalne pytanie, czy potrafiłoby także odejmować. Rozważmy następującą kombinację sygnałów sterujących:

EX	WX	EY	WY	c-1
1	0	1	1	1

Zatem wartość Rejestru X jest przepisana na wejście ALU, zawartość Rejestru Y jest podawana w postaci zanegowanej i do wyniku jest dodana jeszcze jedynka, czyli nasze ALU wykona wtedy operację X + Y' + 1; dokona dodawania do zawartości Rejestru X liczby -Y wynikiem czego będzie różnica pomiędzy wartością X i Y. Operacja ta jest znana pod mnemonikiem SUB(X,Y). Oczywiście można także od Y odjąć X, co wymaga by: E_X = 1 i W_X = 1, E_Y = 1 i W_Y = 0 oraz c_-1 = 1 (SUB(Y,X)). Być może jest to dość zaskakujące, że niewielka modyfikacja w wartościach sygnałów sterujących prowadzi do sytuacji, w której ALU jest w stanie wykonać operacje dodawania, ale i odejmowania, ale powszechnie wiadomo, że odejmowanie jest operacją dodawania liczby ujemnej. Jak widać w przypadku ALU spostrzeżenie to działa bez zarzutu.

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	0	1	1	1		X+Y'+1		SUB(X,Y)
1	1	1	0	1		X'+Y+1		SUB(Y,X)

W zasadzie odkryliśmy już niemal wszystkie tajemnice analizowanego ALU, ale pozostało nam jeszcze kilka „ciekawostek”. Jedna z nich pojawi się właśnie teraz. Oto następująca kombinacja sygnałów sterujących:

EX	WX	EY	WY	c-1
1	0	0	1	0

Oznacza ona, że do liczby znajdującej się w Rejestrze X dodane zostaną `same jedynki' (jeżeli E_Y = 0 i W_Y = 1, to na każdym bicie pojawia się 1). Z pozoru zatem jest to operacja, która oznaczałaby zwiększenie zawartości Rejestru X aż o 15, co w każdym przypadku oznaczałoby przepełnienie, ale można jej przyjrzeć się nieco bliżej i zauważyć, że jest jeszcze inna interpretacja tej operacji. Oto przykład: dodajmy pisemnie w systemie binarnym do liczby 10₍₁₀₎ czyli 1010₍₂₎ liczbę 1111₍₂₎.

	C3	Si				Liczby
Przeniesienie	1	1	1	0
		1	0	1	0	10(10)
			1	1	1	1	15(10)
		1	1	0	0	1	Suma

Oczywiście wynik jest 5-o bitowy, ale jeżeli popatrzymy tylko na ostatnie 4 bity naszego wyniku (pominiemy zatem bit przeniesienia c₃), to okazuje się, że w wyniku przeprowadzonego dodawania na S_i pojawiła się liczba o jeden mniejsza. Nie jest to przypadek (czytelnik pozwoli sobie sam sprawdzić, że za każdym razem wynik takiego dodawania będzie o jeden mniejszy niż pierwszy składnik sumy) i w rzeczywistości analizowana przez nas kombinacja pozwala na zmniejszanie o 1. Rodzi się pytanie: dlaczego? Odpowiedź jest dość prosta - zanegujmy wszystkie bity w 1111 i dodajmy doń 1 by zobaczyć, że w rezultacie otrzymamy liczbę 0001₍₂₎, czyli w analizowanym przypadku 1111₍₂₎ oznacza po prostu -1 w kodzie U2 (w ogólności liczba -1 zawsze w kodzie U2 składała będzie się z samych jedynek, niezależnie od tego ilu bitowa będzie jej reprezentacja). Generalnie zmniejszanie o 1 nazywane jest dekrementacją a mnemonik tej operacji to DEC(∙). Podsumowując: zaprezentowana w tabeli kombinacja sygnałów sterujących pozwala na dekrementację liczby w Rejestrze X, ale także pokazuje, że takowa dekrementacja jest możliwa w przypadku liczby w Rejestrze Y. Zarówno operacja inkrementacji (INC()) jak i dekrementacji (DEC()) są jednymi z podstawowych w przypadku programowania, bowiem często w kodzie różnego typu programów w zależności od użytego języka programowania można spotkać linie typu: i:=i+1; i--; itp.

EX	WX	EY	WY	c-1		Si		Mnemonik operacji
1	0	0	1	0		X+0+1111		DEC(X)
0	1	1	0	0		0+Y+1111		DEC(Y)

W zasadzie zostały pokazane już wszystkie bardziej znaczące operacje, jakie potrafi wykonywać nasze ALU, choć można wskazać i jeszcze inne, np. gdy wszystkie sygnały sterujące są ustawione w 0, to następuje operacja wyzerowania całego układu (mnemonik RESET()), a gdy są ustawione następująco : E_X = 0 i W_X = 1, E_Y = 0 i W_Y = 1 oraz c_-1 = 1, to zarówno wyjście S_i jak i c₃ zostaną ustawione w stan wysoki (mnemonik SET()). Oczywiście możliwe są także operacje typu INC(ADD(X,Y)) (dla : E_X = 1 i W_X = 0, E_Y = 1 i W_Y = 0 oraz c_-1 = 1) lub też np. X + 0 + 0 rozumiana jako przesłanie liczby X na wyjście S_i jednostki ALU (oznaczenie mnemonikiem MOV(X) dla liczby X lub MOV(Y) dla liczby Y), ale nie będziemy nimi się tu zajmować. Warto jednak zapamiętać, że tak prosta konstrukcja pozwala w zasadzie na wykonanie wszystkich operacji arytmetycznych (przypomnijmy, że mnożenie to wielokrotne dodawanie, a dzielenie to wielokrotne odejmowanie) oraz jednej operacji logicznej (negacji CMPL(∙)) - brakuje nam jeszcze sumy i iloczynu logicznego, by powstał niemal „procesor”. Oczywiście w rzeczywistości tego typu układy są o wiele bardziej skomplikowane, ale zasadnicza idea ich konstrukcji pozostaje zbliżona do zaprezentowanej w opracowaniu; nie ma w niej w istocie rzeczy nic nadzwyczajnego. Być może wśród wielu osób informacja ta będzie lekkim rozczarowaniem, bo oto okazuje się, że taki mały komputer można zbudować niemal w pokoju, ale z prezentowanymi dotychczas rozważaniami wiąże się jeszcze jedna kwestia. Zauważmy, że oprócz informacji nt sygnałów sterowania, dla każdej ich kombinacji podawaliśmy tzw. asemblerowy mnemonik. Osoby interesujące się programowaniem wiedzą doskonale, ze programy można pisać nie tylko w językach wysokiego poziomu (Pascal, C, C++, Fortran, Algol itd.), ale także w oparciu o znajomość asemblera dla danego procesora. Jest to dość wyrafinowana sztuka, bowiem pisanie w asemblerze wymaga sporego doświadczenia oraz pewnej programistycznej wyobraźni. Normalnie w systemie komputerowym po napisaniu programu w języku wysokiego poziomu następuje etap jego kompilacji i translacji na język asemblera; robi to za nas kompilator. Kiedyś jednak tak nie było i trzeba było samemu napisać właściwy kod programu w asemblerze, bo nie były znane języki wysokiego poziomu. Co więcej: kiedyś nawet nie znano asemblera! Jak więc pisano programy? Zauważmy, że każdemu mnemonikowi asemblera odpowiada odpowiednia kombinacja sygnałów sterujących w naszym ALU. To oznacza, że z jednej strony asembler nie jest niczym innym jak kodami sterowania podawanymi na szynę sterującą w systemie komputerowym, ale z drugiej strony pokazuje, ze można by pisać programy w oparciu o te kody. No i kiedyś właśnie tak się robiło - programowanie maszyny polegało na wpisywaniu ciągów zer i jedynek (sposób tego wpisywania, to kolejna ciekawostka, bo istniały różne implementacje: od kart perforowanych, poprzez dziurkowane taśmy, zapis na nośnikach magnetycznych, itd.) oznaczających zarówno sygnały sterujące dla szyny sterowania jak i wartości przetwarzanych danych. Pisano więc programy w języku maszynowym (zero-jedynkowym), co oczywiście było to bardzo trudnym i pracochłonnym zajęciem no i było bardzo łatwo o pomyłkę, ale wśród nas żyją jeszcze ludzie, którzy to doskonale pamiętają. Zapis kodu programu funkcjonował najczęściej w postaci grubego zeszytu pokrytego sekwencjami zer i jedynek a sekwencje te były raczej zrozumiałe tylko dla wtajemniczonego programisty. Dziś nie wyobrażamy sobie, aby pisać programy inaczej jak w C lub nawet różnego typu Visuala'ach niemal za pomocą słow znanych potocznie w języku angielskim, ale kiedyś zbyt wielkiego wyboru nie było - tylko język maszynowy.

Na koniec można by rzec, że właśnie tak działa informatyka: być może bardzo mało ciekawie, ale dość niezwykle efektywnie!

Słowo „początkowo” jest trochę niefortunne, bo należy je odnieść do czasów, gdy komputery były już na tyle powszechne, że sam fakt ich posiadania nie oznaczał, że jest się milionerem lub naukowcem - przyjmijmy więc, że odnosimy je do przełomu lat 80-90 XX w. Można jednak żartobliwie powiedzieć, że dla wielu, zwłaszcza młodych ludzi, dopiero co studiujących i zdobywających swoją wiedzę z zakresu ogólnie rozumianej informatyki, to niemal „prehistoria”.

takiego, jak większość zna ze szkoły podstawowej

przykład jest trochę „tendencyjny”, bo jak się okazuje nie ma znaczenia, czy skonwertowaną liczbę przeczytamy „od dołu do góry” czy też odwrotnie

Pamiętajmy o tym, że największa liczba ujemna to ta, która jest najbliżej 0, zatem musimy brać tu pod uwagę moduły reprezentowanych liczb

Nie oznacza to, że dzielenie nie jest ciekawe samo w sobie

stwierdzenie „dość długo” jest mało precyzyjne, ale należy je odnieść do faktu, że czas potrzebny na mnożenie n-bitowych liczb jest proporcjonalny do liczby bitów. Zauważmy, że jeżeli na wykonanie operacji dodawania pojedynczego bitu potrzebujemy pewien jednostkowy czas, to n krotne dodanie n bitów wymaga czasu proporcjonalnego do n². W rzeczywistości istnieją rozwiązania, które rozwiązują ten problem - zostanie to przedstawione w dalszej części opracowania

wynika to z faktu iż wynik będzie albo w postaci 11.xxx... albo 01.xxx, zatem w drugim przypadku normalizacja nie jest potrzebna

w ten sposób będziemy projektowali tzw. układ kombinacyjny, czyli układ w którym nie istnieje sprzężenie zwrotne przekazujące stany wyjść z powrotem na wejście - innymi słowy w układzie nie będzie pamięci

Co prawda w rzeczywistości takich grup potrzeba 3; wynika to z faktu, że trzecia grupa jest tzw. grupą antyhazardową - temat ten nie będzie tu poruszany, ale jest to problem bardzo ciekawy „sam w sobie”

Proszę wybaczyć ten kolokwializm

Można się także spotkać z mnemonikiem NOT(∙)

Nie będziemy tu wnikali w szczegóły, choć są one bardzo ciekawe

---